基于IGMM-Copula的入库径流过程预报误差随机模拟模型

张验科，张佳新，邰雨航，纪昌明，马秋梅

（华北电力大学水利与水电工程学院，北京 102206）

1 研究背景

入库径流预报误差是水文预报不确定性的一种表现，目前的研究一般将量化其随机性作为研究重点，多采用参数估计［1-2］、非参数估计［3］、最大熵［4］等方法对其分布形式近似描述，取得了大量研究成果［5-9］。考虑到入库径流预报误差往往包含多种统计特征，若采用单一分布，例如正态分布、tLocation-Scale 分布等对其进行拟合，某些情况下虽然可呈现出较好的拟合效果，但由于各分布函数有时在对称性和尾部特征上的表现存在差异，并不能保证总可以找到一种分布形式刚好能够达到预期的要求；同时，已有的研究成果多集中于单一变量或单一预见时刻的径流预报误差的量化分析［10-11］， 而对于多个变量或多个预见时刻的径流过程预报误差的分析相对较少。对于预报调度工作而言，前期的入库径流预报作业多在某一固定时刻以某一固定间隔对预见期内多个后续时刻的入库流量进行预报［12］，而根据对应时刻的历时实测入库流量序列，即可分析得到相应的径流过程预报误差序列。这一预报误差序列反映了整个调度期的预报不确定性，而仅对单一预见时刻的预报误差进行研究，则忽略了调度期内不同预见时刻预报误差间的关联性。因此，需要在寻求单一预见时刻预报误差分布的基础上，综合考虑分析不同预见时刻预报误差之间的相关性，才能更为全面地揭示入库径流过程预报误差的变化规律。

为解决上述入库径流预报误差分布研究中存在的问题，纪昌明等［13］依据高斯混合模型（Gaussian Mixture Model，GMM）在密度函数估计中的高度自适应性，结合高维meta-student t Copula 函数在耦合多个类型边缘分布上的优势，建立了多个预见时刻入库径流预报误差的GMM-Copula随机模型，可实现对入库径流预报误差序列的随机模拟。在该项研究中，GMM-Copula模型是以单一预见时刻径流预报误差分布的拟合结果为基础建立的多维径流预报误差联合分布，在应用过程中仍存在两个关键问题：（1）高斯分布混合个数的确定，这是一个权衡的过程，个数过少会影响拟合的精度，相反则会导致模型过于复杂不利于分析；（2）参数初始值的确定，由于采用的是EM（Expectation-Maximization al⁃gorithm，EM）法［14］求解模型拟合需要的参数，它是一类通过迭代进行极大似然估计的优化算法，需要对高斯混合模型的权重等参数进行初始化，不同的初始参数值会对迭代的结果造成较大的影响，从而决定最终的拟合精度。由于原GMM-Copula 模型对于拟合过程的两个关键问题都未做细致的研究，各个预见时刻的径流预报误差的高斯分布混合个数以及初始参数值的确定存在较大的主观性，难以保证拟合结果的精度，从而得到的模拟误差序列也存在进一步优化的空间。

本文基于AIC（Akaike Information Criterion，AIC）与BIC（Bayesian Information Criterion，BIC）准则［15］选取最优高斯分布混合个数，同时引入数据挖掘中的K-means++算法确定高斯混合模型的初始参数值，对GMM-Copula 模型中的GMM 部分进行改进，以此建立基于IGMM-Copula（Improved Gauss⁃ian Mixture Model Copula）的入库径流过程预报误差随机模拟模型。以雅砻江流域锦屏一级水库短期入库径流过程预报误差分析为例，基于IGMM-Copula 模型，首先对预见时刻为6 h、12 h、18 h 和24 h的入库径流预报误差分布进行拟合分析；其次，将拟合结果作为边缘分布从而建立四维入库径流预报误差的联合分布，据此对误差序列进行随机模拟与统计分析，并与GMM-Copula模型得到的结果进行了对比，验证模型的可行性与合理性。

2 GMM-Copula中高斯混合模型描述及其存在的问题

现假设预报误差为ex(i)t(j)，表示当预报起始时刻为x(i)时，对未来t(j)时刻进行径流预报所产生的预报误差，其中i表示历史预报的次数，i∈(1,2,…，n)；j表示预报的时刻数，j∈(1,2,…，m)。可定义为：

式中：Sx(i)t(j)、Hx(i)t(j)分别为预报流量值和实测流量值。

当进行n次预报后，可得到由n个预报误差序列组成的误差数据矩阵E：

针对时刻t(j)的预报误差ex(i)t(j)，可利用高斯混合模型求其分布，设模型中待估计的参数为θ，则高斯混合模型的概率密度函数可表示为：

式中：p(ex(i)t(j);θ)为高斯混合分布的概率密度函数；αk、uk、σ2k分别为第k个高斯分布的参数，分别代表权重、均值和方差，且K表示高斯混合模型中的高斯混合个数。

从式（3）中可知，若要求解单一预见时刻误差分布拟合的表达式，则需要对参数αk、uk、σ2k进行估计，而直接对原式进行最大似然估计则会产生对数的和，求解十分困难，因此采用EM法［14］对参数进行推求。具体的求解步骤如下。

（1）进行EM 算法中的E 步（求期望值），提出一个隐变量γik，γik∈{0,1}，表示第i个样本是否来自于第k个高斯分布，k=1，…，K。将γik引入式（3），得到单个样本完全数据的对数似然函数，如式（4）。对参数θ进行初始化，其中ak=1/K，uk设为随机数，σ2k取1，根据利用贝叶斯定理求解γik的后验概率P(γik=1|ex(i)t(j),θ)，见式（5）。

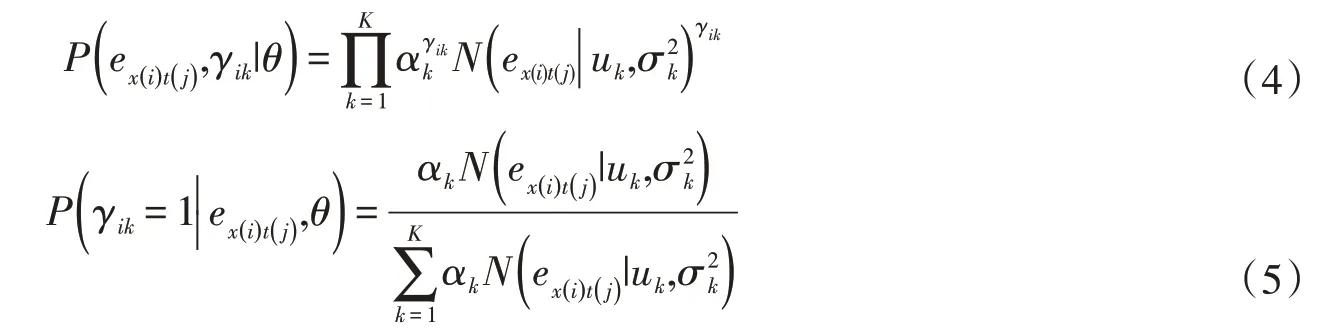
（2）进行EM 算法中的M 步（求最大值），由式（4）得到全部样本完全数据的对数似然函数，见式（6）。依据式（6）分别对αk、uk、σ2k求偏导，令似然函数值为0，求出更新后的参数分别如式（7）所示。

（3）不断迭代步骤（1）和（2），重复更新αk、uk、σ2k，直到前后两次迭代结果的变化幅度小于一个设定值ε，则终止迭代，即|θ-θnew|≤ε，θnew代表更新后的参数值，ε通常取10-4。

GMM-Copula 模型在对单一预见时刻误差分布进行估计的过程中，由于涉及到高斯混合个数K的选取，而通过人为确定的常规方法主观性太强，尤其在于相邻时段的预报误差分布可能具有不同的特征，若高斯混合个数选取不当，势必会对最终拟合的精度造成影响；同时，模型采用随机抽取确定初始参数值的方式同样不严谨，初始值的不同会影响最终迭代得到的参数，从而影响最终分布拟合的结果。本文基于AIC与BIC准则选取最优的高斯混合个数，同时采用K-means++算法确定高斯混合模型参数的初始取值，建立基于IGMM-Copula 的入库径流过程预报误差随机模拟模型。模型在优化单一预见时刻径流预报误差分布拟合方法的基础上，考虑了各个预见时刻之间的相关关系，并结合随机抽样理论，可实现对多个预见时刻入库径流过程误差的随机模拟。

3 基于IGMM-Copula的入库径流过程预报误差随机模拟模型

模型主要从两个方面叙述，提出GMM-Copula 模型改进的两个方面；2.3 节描述了如何利用IGMM-Copula模型建立多个预见时刻的径流预报误差联合分布以及误差序列随机模拟的步骤。

3.1 基于AIC与BIC准则的最优高斯分布混合数选取AIC与BIC都作为衡量统计模型拟合优良性的标准，与AIC不同的是，BIC引入了与模型参数个数相关的惩罚项，考虑了样本数量，更适合样本数量较多时的情况。对应的计算公式如下：

式中：K为模型的参数个数，在本文中表示为高斯混合模型中的高斯混合个数；n为预报误差样本个数；L为模型参数求解中所对应的似然函数。

当模型的参数变动时，AIC 及BIC 的值越小则表示模型的拟合效果越好。由于高斯混合模型中K≥2，因此选择以K=2作为起点，通过逐一列举的方式计算模型拟合预报误差分布的AIC 及BIC 的值，并选取对应AIC及BIC值最小的K值作为当前预见时刻误差分布最优的高斯分布混合个数。

3.2 基于K-means++的参数初始值确定K-means++算法是一种确定聚类迭代初始起点的算法［16］，一般用于初始化K-means++聚类算法的聚类中心。高斯混合模型本质上作为一种聚类模型，其原理是通过计算每个数据所属的高斯类从而实现聚类的效果，因此同样可以利用K-means++算法进行预分类，并根据预分类的结果计算高斯混合模型的初始参数值，其具体步骤如下：

（1）从单一预见时刻误差数据集中随机选定与最优高斯分布混合数K相同数目的初始聚类中心；

（2）计算每个误差数据ex(i)t(j)与之最近一个聚类中心的马氏距离D(ex(i)t(j))；

（4）重复（2）（3），直至每一个聚类中心不再变化为止；

（5）依据得到的聚类中心将误差数据聚类，并计算每个类的均值u′k与方差(σ2k)′作为迭代的初始值，其中权值的初始值

当初始参数值确定后，利用EM算法迭代计算则可得到最终的αk、uk、σ2k，带入式（3）即可得到单一预见时刻的误差分布表达式。

3.3 多个预见时刻径流预报误差联合分布建立及应用meta-elliptic Copula 函数族中的高维meta-stu⁃dent t Copula［17］、高维meta-Gaussian Copula［18］是水文中常用的两类分布，由于在预报模型在预报过程中受到的干扰因素难以量化，可能会在某一时间点产生与均值偏离较大的预报误差，而高维meta-Gaussian Copula 不具有尾部相关性，因此本文在推求各个预见时刻误差分布的前提下，选用高维me⁃ta-student t Copula建立多个预见时刻径流预报误差间的联合分布，可表示为：

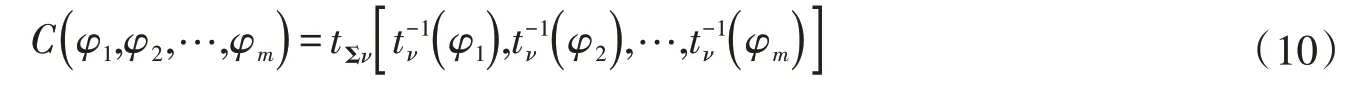
将其展开可得：

式中：C(φ1,φ2,…,φm) 为m维随机变量联合分布，φ1，φ2，…，φm分别表示m个预见时刻的入库径流预报误差；tΣν为ν个自由度的t分布函数，其协方差矩阵为Σ；t-1ν(·)为自由度为ν的t分布的逆函数；Γ(·)为伽马分布；X为不同预见时刻的预报误差变量矩阵，X=(φx(i)t(1),φx(i)t(2),…，φx(i)t(m))；φ为被积函数变量矩阵，φ=[φ1,φ2,…，φm]T。

当对整个入库径流预报过程进行不确定性分析时，需要依据入库径流过程预报误差联合分布对误差序列进行随机抽样，主要分为如下两步。

（1）依据联合分布C(φ1,φ2,…，φm)生成随机序列矩阵ω=[ω1,ω2,…，ωm]，ωj表示对应预见时刻误差分布的累积分布概率。

（2）推求对应预见时刻误差分布的逆累积分布函数Fj-1(φi)，将随机序列矩阵ω带入该函数，可得到模拟的入库径流过程误差序列，表示为e′=(F1-1(ω1) ,F2-1(ω2),…，Fm-1(ωm))。

基于IGMM-Copula的入库径流过程预报误差随机模拟模型的研究流程如图1所示。

图1 基于IGMM-Copula的入库径流过程预报误差随机模拟模型的流程

4 基于IGMM-Copula的入库径流过程预报误差随机模拟模型

锦屏一级水电站水库在雅砻江下游“锦官电源组（锦屏一级、锦屏二级、官地）”梯级水电站水库群中起控制性作用，其入库径流预报采用的是三水源新安江模型［19］，具体是以每天早上的8 点作为预报起点，以连续预报的形式对当天14点、20点、次日2点及次日的8点进行径流预报（依次对应预见时刻为6 h、12 h、18 h和24 h），一次预报可得到未来一天的预报流量序列，以此制订水电站水库的调度计划［20-21］，预报的实施过程见图2。自投产以来，存在因来水预测误差造成水库运行水位超出控制范围而需要调整发电计划的情况［22］，本文选用锦屏一级水电站水库2014年1月1日至2017年9月23日每日的实测及预报径流资料，根据式（1）计算得到未来24 h 内的预报误差序列（每个序列包含4 个预见时刻的预报误差），共得到1362 条预报误差序列样本，而后利用本文所提方法建立基于IGMM-Copula 的入库径流误差随机模拟模型，一方面通过求解各预见时刻的径流预报误差分布，分析了确定性预报模型产生预报误差的统计特征和分布规律，同时也考虑了不同预见时刻下预报误差的相关性，实现了对预报误差的多元联合模拟，为根据预报资料制订水库调度计划，提供了更多参考信息。

图2 锦屏一级水电站水库径流预报实施过程

4.1 各预见时刻径流预报误差分布求解基于IGMM-Copula模型中的分布拟合部分（此处称为IGMM）对各预见时刻径流预报误差经验分布进行拟合，首先需要确定各时刻预报误差的最优高斯混合数，在原GMM 模型中，由于没有相应的指标作为参考，作者偏向于参数较少，更容易求解的模型结构，因此最终选取的高斯混合数为K=2。现以K=2 为起点，根据逐一列举法计算不同K值下的AIC 及BIC的值。其计算结果如表1。

从表1可以看出，以6 h、12 h、18 h、24 h 径流预报误差为基础建立的IGMM 在AIC 及BIC 的值取得最小时，对应的最优高斯混合数为K=3，据此可建立对应权重的IGMM 对各预见时刻径流预报误差进行拟合，表2为基于IGMM 的各预见时刻径流误差分布参数估计值。为体现IGMM 在误差分布估计方面的优势，将原GMM 与单高斯分布（SGM）作为比较模型。其中，GMM 高斯混合个数的选取及参数初始值的确定均按照原文献里介绍的方法进行计算。

表1 不同高斯混合数下各预见时刻径流预报误差IGMM的AIC及BIC的值

表2 基于IGMM的各预见时刻径流误差分布参数估计值

图3是3 种模型对不同预见时刻径流预报误差的拟合效果图，其中实测预报误差样本个数n≥1000，据此做出的频率直方图总体呈现出对称的形状，误差数据大部分集中在0值附近，SGM 拟合得到的概率密度函数较为矮胖，在峰部的集中度与频率直方图相差较远，而IGMM 与GMM 由于自适应性较强，两者的拟合结果在数据集中的位置更契合频率直方图，在图中体现为概率密度函数的形状更为尖瘦，因此能更大程度的反映实测预报误差样本所展现的规律，这也印证了高斯混合模型在概率密度估计中的优越性。同时，由于不同预见时刻的径流预报误差具有不同的特征，而人为确定GMM 中高斯混合数与参数初始值难以达到最佳的拟合效果，尤其对于预报误差数据峰部的拟合，基于IGMM 得到的拟合曲线的拟合效果明显优于GMM，其原因主要在于IGMM 对高斯混合数进行了优选，并对参数初始值进行了预计算，因此拟合曲线更贴近于频率直方图。

图3 三种模型对不同预见时刻径流预报误差的拟合效果

4.2 模型适用性检验适用性检验包括拟合优度检验与后验检验，拟合优度检验的目的是用历史数据来检验模型是否能够反映径流误差的随机特性［23］，具体包括χ2检验、t-检验、K-S 检验等，其中K-S 检验是一种检验单个总体是否服从某一理论分布的非参数检验方法，相比于χ2检验能够更充分地利用样本信息，适用于连续和定量数据［24］。K-S检验统计量Dn定义见下式：

式中：Dn越小说明拟合优度越高；Fn(·)为经验分布函数；Ft(·)为假设的理论分布函数。分别对改进高斯混合模型、核密度估计模型以及单高斯模型进行K-S 检验，显著性水平设置为0.01，其计算结果见表3。

从表3可看出，IGMM 及GMM 都通过K-S 检验，即两者与经验分布在显著性水平为0.01 的前提下没有显著性差异，验证了IGMM 与GMM 模型在径流预报误差密度估计中的可行性，同时IGMM 在各预见时刻下误差拟合曲线的Dn值都为最小，说明其对于单一预见时刻径流预报误差经验分布的拟合优度最高。

表3 模型K-S检验指标值

后验检验的目的是定量评估概率模型与数据观测分布（即统计直方图）之间的差异［25］，采用式（13）的均方根误差εRMSE与式（14）的平均误差百分数εMAPE作为指标对求得的各预见时刻径流误差分布进行检验，得到的指标越小，说明拟合模型与数据观测分布之间的差异越小，其计算结果见表4。

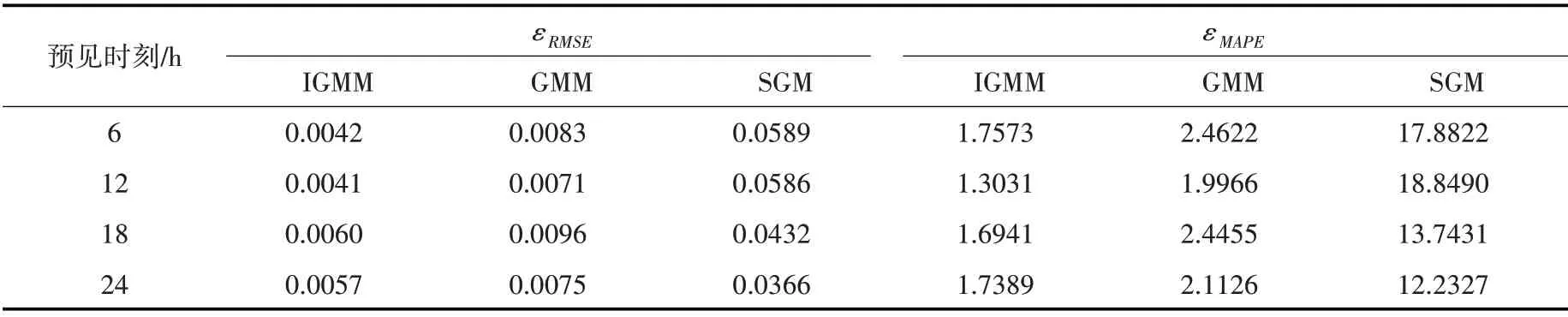
表4 模型后验检验指标值

由表4可见，对于所有预见时刻而言，基于IGMM 得到的误差分布的εRMSE都保持在0.06 及以下，εMAPE都保持在1.8 以下，相较于SGM 与GMM，在两指标上的表现最好，说明基于IGMM 得到的各预见时刻误差分布与数据观测分布之间的差异相差最小。

为分析不同预见时刻间径流预报误差分布的差异，图4将IGMM 拟合得到的各径流预报误差分布曲线汇总，从图中可观察到，随着预见时刻的增加，误差分布形状逐渐从“尖瘦型”变化为“矮胖型”，表面预报不确定在随时间的增加而增大，符合确定性预报模型的预报规律。

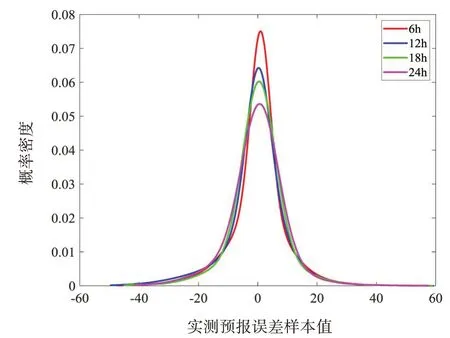
图4 各预见时刻径流预报误差分布曲线

4.3 径流预报误差序列随机模拟首先分析预见期内各时刻径流预报误差两两间的相关性，et(6)、et(12)、et(18)、et(24)分别表示6 h、12 h、18 h、24 h 的径流预报误差，采用Kendall 相关系数作为相关性的度量并进行双侧显著性检验，设置零假设为：变量et(6)、et(12)、et(18)、et(24)没有相关性，显著性水平为0.05，其计算及检验结果如表5所示。

从表5可知，双侧假设检验的P 值均小于显著性水平，因此拒绝零假设，认为各预见时刻的预报误差均存在正相关性，考虑利用高维t-Copula建立径流过程预报误差的联合分布并据此进行误差序列抽样，实现对预报误差序列的随机模拟。

表5 各预见时刻径流预报误差间的Kendall相关系数

为检验高维t-Copula 对多维误差的适用情况，根据图形分析法原理，以IGMM 求得的6 h、12 h、18 h、24 h径流预报误差分布为例，分别按式（11）与式（15）计算误差的理论联合分布概率和经验联合分布概率，并点绘两者的关系图，见图5。

图5 理论联合分布概率与经验联合分布概率关系

式中：Nq为同时满足X1≤ex(1)t(j)，X2≤ex(2)t(j)，…，Xn≤ex(n)t(j)的样本个数；N为样本总量。

其中，由于实测预报误差样本个数较大，因此绘出的散点图比较密集（图5中蓝色数据点），形状趋向于一条线，由趋势线的斜率可看出，图中的点都大致落在45°对角线两侧，理论联合分布概率和经验联合分布概率的RMSE为0.00907，表明利用高维t-Copula建立多个预见时刻径流预报误差的联合分布是合理可行的。

现根据IGMM 求出的各预见时刻径流预报误差分布为边缘分布，以高维t-Copula 作为连接函数，建立基于IGMM-Copula 的入库径流过程预报误差随机模拟模型，并与GMM-Copula 模型进行对比，按照2.3 节的步骤分别利用两模型对预报误差序列进行500 000 次随机模拟，计算IGMM-Copula 与GMM-Copula模拟预报误差的统计参数，计算结果见表6和表7。

表6 GMM-Copula模拟预报误差与实测预报误差的统计参数值

表7 IGMM-Copula模拟预报误差与实测预报误差的统计参数值

由表中可知，相较于GMM-Copula模型，IGMM-Copula模型各预见时刻模拟预报误差的统计参数更贴近于实测预报误差，而在18 h 时，由于误差均值较小，模型模拟预报误差与实测预报误差的变差系数产生了较大的差异，而IGMM-Copula 模型明显更优于GMM-Copula 模型，这也反应了不同的预报误差边缘分布会对抽样结果造成一定程度的影响。从统计参数的整体变化趋势分析，IGMM-Copula 模型的模拟预报误差能与实测预报误差保持一致，说明模型能够很好的反映径流预报误差序列的统计特性，可作为对预报结果进行修正的参考依据。

5 结论

本文在GMM-Copula 模型的基础上，对高斯混合数的选取以及初始参数值的确定进行了改进，建立了基于IGMM-Copula 的入库径流过程预报误差随机模拟模型，模型可运用于单个预见时刻及多个预见时刻的径流预报误差分析与模拟。以锦屏一级水库为例的结果表明：对于单一预见时刻的径流预报误差的描述，IGMM-Copula 模型在拟合优度检验及后验检验中皆优于单高斯与GMMCopula 模型；通过IGMM-Copula 模型模拟得到的误差序列的均值、方差和变差系数相较于GMMCopula 模型更贴近于实测误差序列，统计参数的变化规律基本一致，验证了模型的可行性，不仅为研究径流预报误差提供一种新的方法，也为水库短期优化调度计划的制订提供了更为丰富的参考信息。