基于滑动时间窗的稠密子图发现算法研究
2021-07-16田朝霞曲贤菲
田朝霞 张 俊 陈 旭 曲贤菲
(大连海事大学信息科学技术学院 辽宁 大连 116026)
0 引 言
当今,动态性已经成为建模为图和网络的数据分析系统和应用程序的明显特征,如社交网络分析、生物数据分析、推荐系统和路径规划[1]。因此,动态网络引起了行业和学术界的重视,实际上,通常使用动态网络的各种替代术语,如时态网络、动态图、演化网络、时间依赖图和图流等[1-2]。现实世界的网络本质上是动态变化的,实体(节点)不断建立新的关系(边),移除旧的关系。分析网络的时间维度可以提供有关其结构和功能的有价值的见解,例如,可以揭示时间模式、概念漂移、周期性和时间事件等[3]。
稠密子图发现是一个基本的图挖掘问题,已经成为广泛的数据分析任务中的原语,如社区检测[4]、事件检测[5]、链接垃圾邮件检测[6]和计算生物学[7]等。在理论计算机科学中已经广泛研究了稠密子图发现问题,由于该问题与实际应用的相关性,在社区数据挖掘中引起了相当大的关注。社交网络中紧密连接的用户可能对应于社区,也就是有相似兴趣或与同一组织(例如大学或公司)相关联的用户组。突然在推文中共同出现的城市、个人和公司名称等实体可能表明涉及相应实体的事件正在发生[2]。
在现实应用中,图数据会随时间发生动态变化,也就是所谓的时态图,时态图有两种变化形式:一种是图的拓扑结构变化,图中的节点和边随时间发生插入和删除,从而导致图的结构发生变化;另一种是图的内容变化,图中的节点和边所表征的数据值或者对象内容发生变化。本文更多关注时态图的拓扑结构变化对稠密子图发现结果的影响。当处理时态网络时,首先要确定如何处理时间维度,即识别哪段时间是可以发现稠密子图的时间间隔。本文算法不是先验地定义这些间隔,而是研究自动识别稠密子图的间隔的问题,因此能够在时态网络中发现一系列稠密子图,捕获网络生命周期中发生的有趣事件的演变。
为了得到更具体的理解,请考虑以下几种场景的事例:
(1) 许多不同机构的一组研究人员正在合作开展一个大型项目,小组成员参加他们各自的日常活动,但每隔几周或几个月,在项目会议或可交付的截止日期之前,小组成员间会参与许多与项目有关的活动。
(2) 一群Twitter用户对某一技术产品感兴趣,他们积极地在博客评论并互相评论彼此的帖子,尽管这之间的相互联系非常稀疏,但持续时间长,并且在新产品发布之后显著增强。
(3) 在线社交媒体中的故事识别[8]通过实体之间的稠密子图自动发现新兴故事,了解故事如何随时间的推移而演变。例如,当一个故事消失另一个故事出现时,实体间的一个稠密子图消失,另一个出现。通过将时态网络的时间线分割成区间,并识别每个间隔中的稠密子图,可以捕捉主要故事随时间的演变。
对于时态网络,只有很少的论文提出了发现时间上连续的最稠密子图的方法。与本文工作最相似的是找到所有或k个快照中存在的重子图[8],另一个相关工作侧重在时态网络中找到由k个散乱区间覆盖的稠密子图[9]。然而这两种方法都只发现了一个最稠密子图。
本文的目标是研究在滑动时间窗中发现稠密子图的问题,为了实现这一目标,采用动态稠密子图的现有工作设计一个快速的近似算法,结合滑动时间窗将时态网络划分成k个非重叠的间隔,使得间隔内能够发现最大稠密子图。
本文的主要思路如下:
(1) 研究了滑动时间窗中的最大稠密子图问题,利用动态稠密子图的现有工作,设计一个快速的动态近似算法。
(2) 结合时间窗大小将时态网络的时间线分割成k个非重叠间隔,每个间隔内能够发现具有最大密度的子图。
(3) 在真实数据集上进行实验,验证了本文方法的有效性,并解释结果的合理性。
1 相关工作
在稠密子图中对图进行分区是一个公认的问题,现有研究大部分采用密度定义的平均度概念[10],在此定义下,可以在多项式时间内找到最稠密子图[11]。另外,Charikar[12]开发了一个近似贪婪算法,它在图大小的线性时间内运行。Epasto等[2]开发了在流式场景中维护平均度最稠密子图的算法。其他密度定义通常难以通过有效的启发式方法得到问题的近似解。
现有研究大都关注动态图,建立节点和边添加或删除的模型,研究网络演化的不同方面,包括稠密集群的演化[13]。另一种建模时态图的经典方法是图快照,分别在每个快照中(或合并先前快照的信息)找到结构,然后总结已发现结构的历史行为[14]。这些方法侧重于快照中发现的稠密结构的时间一致性,并假设已经给出了快照。与此不同,本文工作是将瞬时交互聚合到任意长度的时间轴分区中。
许多动态图研究致力于事件检测问题,Akoglu等[15]涵盖了该主题的最新研究,大部分研究侧重比较不同的图快照,目的是检测图结构发生重大变化的快照。与其他事件检测问题相比,本文研究主要目标是同时发现事件的子图和相应的时间间隔。与动态图事件检测类似,构建一个包含时态信息的静态图(或一系列静态图)是动态图研究的常用方法, Rosvall等[16]的动态聚类方法将时间数据嵌入到静态图中,使用历史时态数据学习二跳路径的概率以产生聚类。但发现的聚类在时间上是全局的,没有检测到相关的突发时间间隔,并且没有时间约束。
与本文工作最相似的是Rozenshtein等[9]的研究,考虑了在时态网络中发现最稠密子图的问题,然而他们并不旨在创建时间分区,且他们发现的是边出现在k个短间隔内的单一的稠密子图。本文工作是划分间隔并仅考虑跨越连续间隔的图。Semertzidis等[8]考虑一组图快照,并搜索一个或多个间隔诱导的单个重子图,探索持久性重子图问题的不同公式,包括最大平均密度。Bogdanov等[17]提出了在时间演变网络中挖掘重子图的方法,但其仍然是基于网络快照,因此对边界量化效果很敏感,且发现的重子图的概念基于边权重而不是基于密度。
总之,与已有研究相比,本文希望能够在时态网络中发现一系列稠密子图,捕获网络生命周期中发生的有趣事件的演变。
2 时态稠密子图问题定义

(1)

(2)

下面介绍与稠密子图相关的其他概念:图核、核心分解和顶点的诱导核心子图。


V=C0⊇C1⊇…⊇Cl⊇∅
(3)
其中每个Ci都是一个j-core。

另外,使用κH(v)表示由H诱导的子图中顶点v的核数,G(H)=(H,E(H))的子图的最大核(或主核)用Cl(H)表示,G的主核仅用Cl表示。

换言之,诱导子图包含可从v到达并具有相同核数κ(v)的所有顶点。
本文在滑动时间窗边流中处理图,根据这个模型,问题的输入是边流形式,边ei是流的第i个元素,即边ei有时间戳i,滑动窗口Wt(x)定义为在时刻t长度为x的et-x+1和et间到达的所有边的集合:
Wt(x)={ei,i∈[t-x+1,t]}
(4)
对于每条边ei=(u,v),u和v出现在时刻i,使用Vt(x)表示时刻t出现在长度为x的滑动窗口中的顶点集,在时刻t长度为x的滑动窗口中的图定义为Gt(x)=(Vt(x),Wt(x))。
下面定义本文研究的问题,即以滑动时间窗进行分割,在时态网络中找到一系列稠密子图。

3 时态稠密子图发现算法
本文算法的目标是在线更新稠密子图,但动态流更新稠密子图有两个问题:① 如何减少稠密子图的搜索空间;② 如何分割整个图得到子图。
为了解决上述问题,本文提出两个假设性判断。首先,由于稠密子图由相对高度的顶点形成,可以通过仅跟踪这些高度顶点找到稠密子图;其次,这些子图可以在图更新时进行局部更新,而不影响图的其他部分。
基于这两点,本文提出一种新算法,通过仅考虑高度节点减少搜索空间,并将整个图划分为更小的子图,从每个子图中找到稠密子图。
3.1 存储高度顶点的数据结构
提出一个增量数据结构,存储一个强连接的子图,用D表示,子图维护以下不变量:①D内的每个顶点v∈D的核数κD(v)等于D的主核(Ce(D));②D内所有的顶点是连通的。这些不变量确保D中的所有顶点具有相同的核数,根据定义这是D的主核。在处理图更新时,D会维护这些不变量。
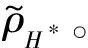
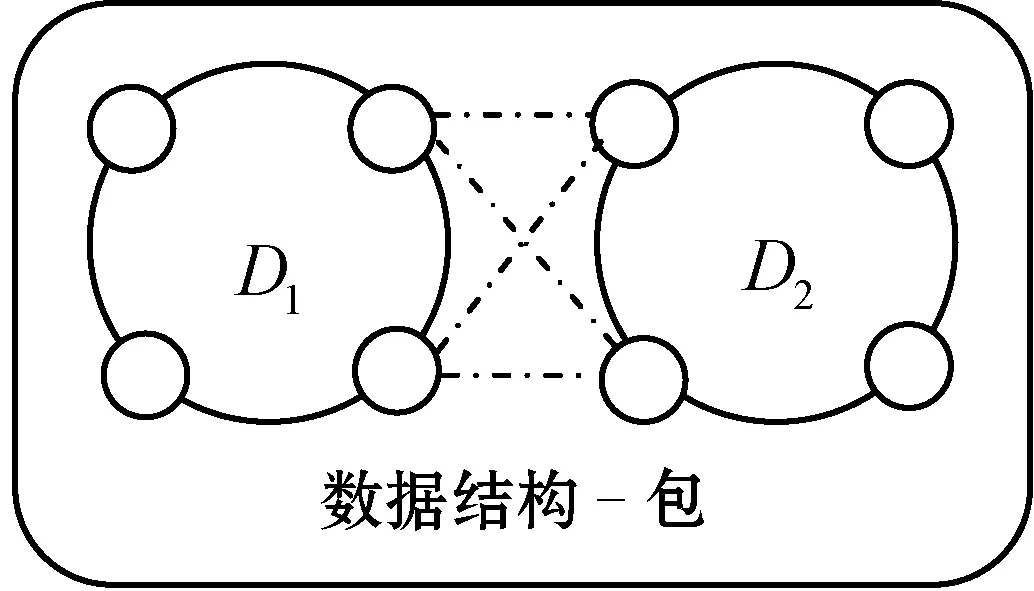
图1 存储高度顶点的数据结构图
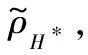
3.2 添加顶点/边操作
1) 添加顶点操作。如第2节所述,更新以边流的形式出现,定义了添加顶点算法,作为添加边算法的子程序,当添加边中至少一个顶点是高度顶点时触发此算法,需要考虑两种情况:(1) 包已经包含高度顶点;(2) 包不包含高度顶点。在这两种情况下,目标是将新顶点添加到一个D。
算法1描述了添加顶点的算法,对于第一种情况,算法扫描包找到包含顶点的D并返回它,对于第二种情况,算法首先识别候选D,然后将顶点分配给其中一个候选D,候选D具有小于或等于新顶点内度的主核数(κu(D)≥Ce(D)),在候选D中新顶点被分配给具有最大内度du(D)的D。
顶点加入到D中,D的核数可能会增加,需要删除核数低于D的主核的顶点,通过类似bin排序的方法基于度对顶点进行排序,可以在线性时间内有效更新稠密子图。
算法1添加顶点算法
1.H*←∅;
2. forDi∈Bdo
/*识别候选D*/
3. ifu∈Dithen
/*找到包含顶点的D*/
4. returnDi;
5. if (dDi(u)≥Ce(Di) andρH*<ρDi)then
6.H*←Di;
/*候选D具有小于或等于新顶点内度的主核数*/
7. ifH*=∅ then
8.H*←{u};
9. elseH*←H*∪{u}
10. returnH*;
2) 添加边操作。在这种情况下,只有当添加边的至少一个顶点是高度顶点时,才会影响包的状态, 需要考虑两种情况:(1) 只有一个顶点是高度顶点;(2) 两个顶点都是高度顶点。对于第一种情况,算法利用添加顶点的方法把顶点添加到D的包中;对于第二种情况,当两个顶点都添加到D的包中时,算法验证主核是否存在于包中,当两个顶点添加到同一个D时,算法将新边添加到同一个D并确保不变量保持不变。相反,当两个顶点添加到不同的D时,算法验证顶点是否存在于彼此的诱导子图中,并修复两个顶点的主核。算法2描述了添加边的过程。
算法2添加边算法
2. return;
/*只有一个顶点是高度顶点*/
4.Du←AddToBag(u);
6.Dv←AddToBag(v);
7. else
/*两个顶点都是高度顶点*/
8.Du←AddToBag(u);
9.Dv←AddToBag(v);
10. ifDu=Dvthen
11.Du←Du∪{u,v}
3.3 移除顶点/边操作
1) 移除顶点操作。与添加顶点操作类似,首先定义从D的包中移除顶点的过程,移除顶点的方法用作移除边过程的子程序。只有当顶点的度低于最大密度时才会从包中移除顶点,移除顶点不能是主核的一部分,算法从包中的D里移除顶点而不执行其他操作。
2) 移除边操作。利用包确保存在一个核数等于图的主核的D,当其中一个顶点是低度顶点或者两个顶点属于不同的D时,包不需要任何更新。因此考虑其中一个顶点位于高度顶点边界的情况,移除边将顶点从高度移到低度,在这种情况下,算法仅需要从包中移除顶点,而不执行其他操作。如果移除边的两个顶点都是高度的并且属于同一个D,算法从D中移除边,此外,验证并更新影响的顶点的核数,移除边可能会降低最大密度,因此需要向包中添加其度大于新最大密度的顶点。算法3描述了移除边的过程。
算法3移除边算法

/*其中一个顶点是高度顶点*/
2. return;
/*其中一个顶点位于高度顶点边界*/
4. RemoveVertex(u);
5. return;
7. RemoveVertex(v);
8. return;
9. forDi∈Bdo
/*两个顶点都是高度并且属于同一个D*/
10. if (Di∩(u,v)≠∅)then
11.Di←Di(u,v);
/*从Di中移除(u,v)这条边*/
3.4 完整的时态稠密子图发现算法
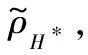
算法4TDSubgraph

输出:H*。

2. Wait for update(Op,u,v),Op∈{Add,Remove};
/*选择添加或者移除*/
3. if Op=Add then;
4. if Add=Vertex; 算法1;
5. else 算法2;
6.else 算法3;
7.returnH*;
下面给出本文算法的复杂度分析,设A为添加的边数,即A包含初始图的边和添加的边,R为移除的边数,得到A+R=O(A),本文将一系列操作的总开销限制在移除边的随机选择定义的概率空间中。本文算法的添加边操作需要O(log(A)log2(n))的时间,移除边操作需要O(log(A)log3(n))的时间,因此算法总的时间复杂度为O(Alog(A)log2(|V|)+Rlog(A)log3(|V|)),同时算法需要O(n2poly(A)logn)的空间。
4 实验与结果分析
为了评估本文算法TDSubgraph,使用社交网络,检查算法的运行时间,分析发现稠密子图的结构特征。实验中使用的所有数据集都是公开可用的。
4.1 数据集


表1 数据集包含的信息
(1) Facebook。该数据集是新奥尔良地区社区中三个月Facebook活动的子集,包含匿名墙贴的列表,子集涵盖2006年5月9日至2006年8月6日的时间段。
(2) Twitter。该数据集在2010年8月至2010年10月期间跟踪赫尔辛基地区Twitter用户的活动。由于用户交互考虑了包含其他用户评论的推文。
(3) Students。该数据集是加州大学欧文分校学生在线社区的活动日志。节点代表学生,边代表消息。使用该数据集的一个子集,涵盖时间范围是2004年6月27日至2004年10月26日。
(4) Enron。该数据集包含从1980年开始超过20多年的大公司高级管理层的电子邮件通信信息。
(5) FacebookL。该数据集由Facebook数据集顺序连接生成,包含1 000万条记录。
(6) TwitterL。该数据集由Twitter数据集连接生成,包含1 000万条记录。
4.2 实验设置
评估本文算法TDSubgraph的性能和效率,主要包括:通过算法发现的稠密子图密度评估性能,运行时间评估算法的效率。其中运行时间是移动滑动窗口所需的平均时间,包括添加新的边、移除旧的边、更新稠密子图。
本文实验的硬件配置是Intel(R) Core(TM) i5-4590 3.30 GHz处理器和8.00 GB内存,所有的算法都用Java实现,每次运行使用的内存不到可用主内存的10%。
本文考虑了两种常用的流排序方案。
(1) BFS。排序是从随机顶点开始的广度优先搜索的结果。
(2) DFS。排序是从随机顶点开始的深度优先搜索的结果。
4.3 最优基线
算法的自然基线Optimal[18]结合了精确的动态编程,并为每个候选区间找到最佳稠密子图。由于Optimal的时间复杂度很高,生成一个包含60个时间戳的小数据集,其中每个时间戳包含一个带有3~6个顶点和随机密度的随机图。改变区间数k的值,图2给出算法结果和运行时间。在这个小数据集上,本文算法能够找到接近最佳的稠密子图,同时明显快于Optimal。
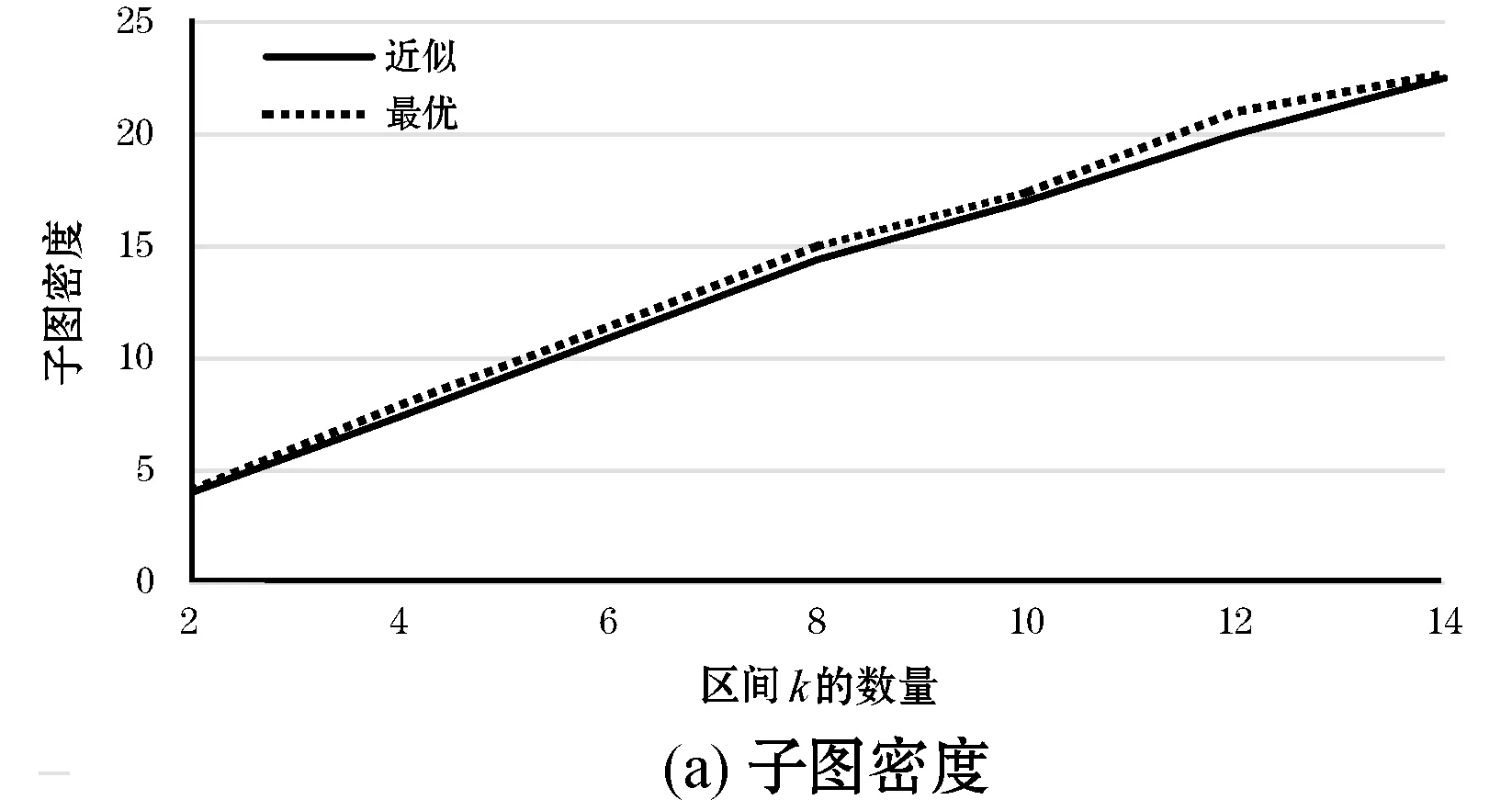

图2 最优和近似算法的比较
4.4 真实数据集上的结果
由于基线算法Optimal在真实数据集上没有很好的可扩展性,本文将算法TDSubgraph与基线kGoptDP[2]和kGoptDS[11]进行比较。kGoptDP算法执行精确的动态编程,但使用近似增量算法搜索稠密子图;kGoptDS算法执行近似动态编程,同时为每个候选区间计算稠密子图。kGoptDP具有2(1+εDP)2近似保证,kGoptDS具有(1+εDS)近似保证。然而这两个算法实际运行也非常慢,本文使用Students和Enron数据集的1 000条记录的子集进行比较。
为了确保公平性,本文给出算法发现的区间内最佳稠密子图的总密度。
本文用近似稠密子图搜索(εDP)和近似动态编程(εDS)的不同参数进行实验。表2给出算法TDSubgraph、kGoptDP和kGoptDS和发现的稠密子图的密度及算法的运行时间。对于这两个数据集,kGoptDS发现了最佳稠密子图,因为该算法具有最佳近似因子。此外,kGoptDS算法的运行时间最长,随着参数εDS的增大,算法运行时间减少,即使是最大的参数值(εDS=2),运行时间仍能达到一个多小时。kGoptDP算法发现了第二好的稠密子图,只是略微优于本文算法(例如εDP=0.1),从表2看出,随着εDP的增大,得到的稠密子图的密度减小。对于这三个算法,随着近似参数增大,发现稠密子图的密度减小,然而密度减小并非像最坏情况表明得那样明显,使用这样的近似参数加快运行时间,TDSubgraph为近似参数提供最快的高性能估计,从表2可以看出,本文算法对参数εDP影响的稠密子图密度的变化更敏感。
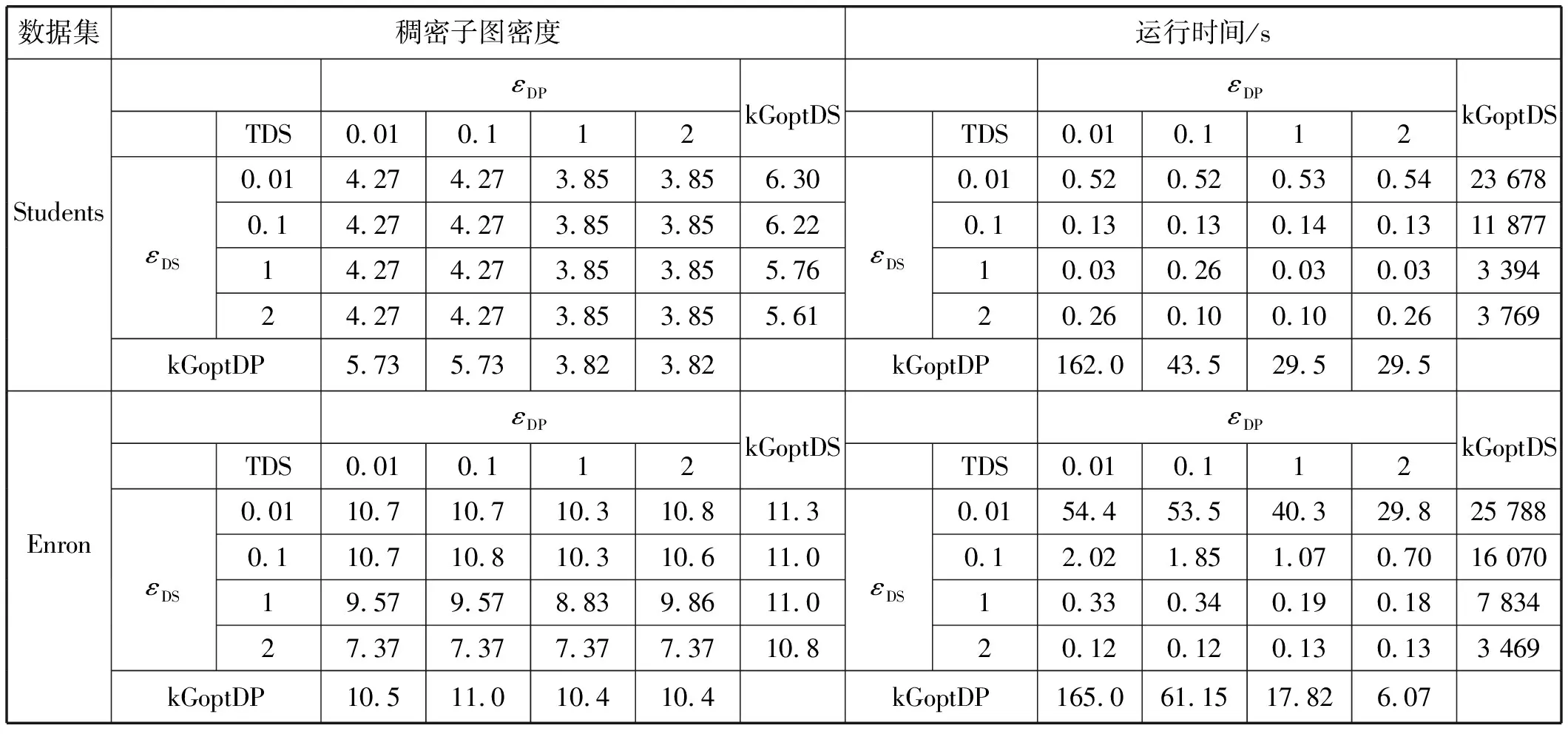
表2 TDSubgraph、kGoptDP和kGoptDS的比较结果
实验使用边流的BFS和DFS两种排序方案,评估不同方案对算法运行时间的影响,设置滑动窗口的大小为x=100k。图3给出算法采用不同流排序方案的运行时间,可以看出,本文算法采用这两种排序方案处理所有数据集时,BFS略优于DFS,因为DFS策略占内存少但速度较慢,BFS策略占内存多但速度较快,整体比较运行时间仍然都优于其他两个算法。
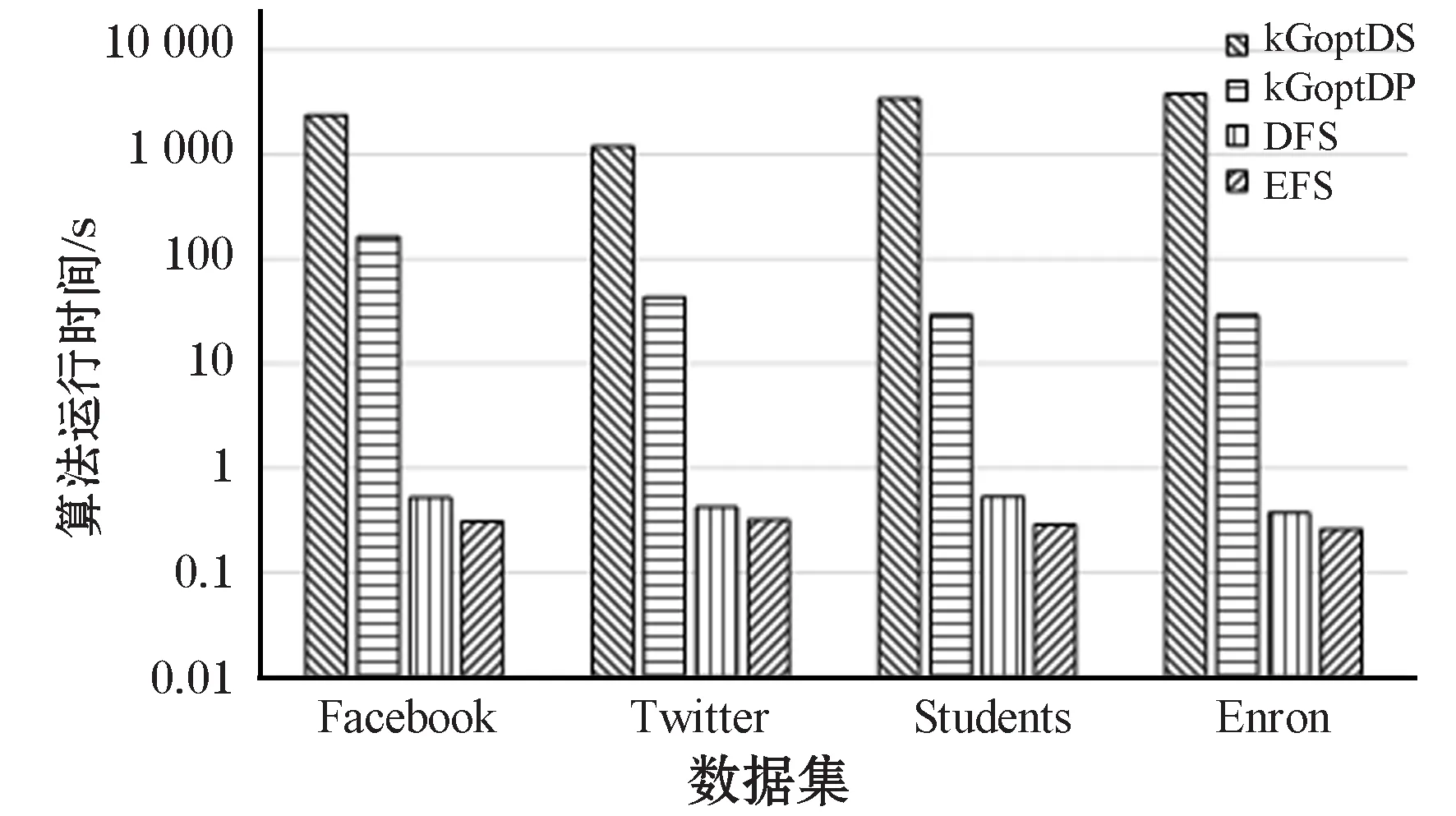
图3 不同流排序方案对算法的影响
4.5 运行时间与可扩展性
图4给出近似参数εDS和εDP的改变对TDSubgraph运行时间的影响。图中结果表明参数εDP对运行时间有重大影响,同时参数εDS在这两个数据集上有很好的扩展性。
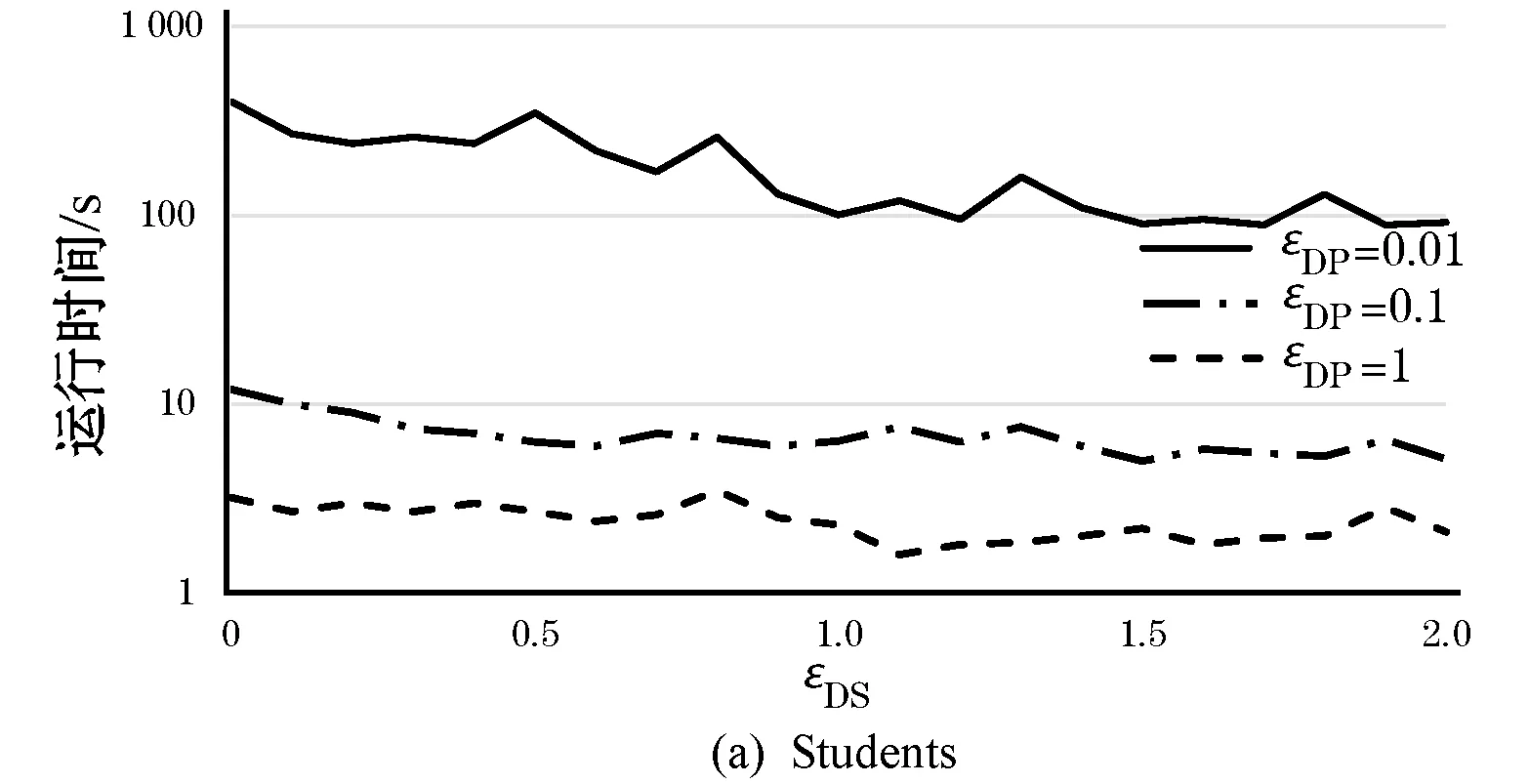
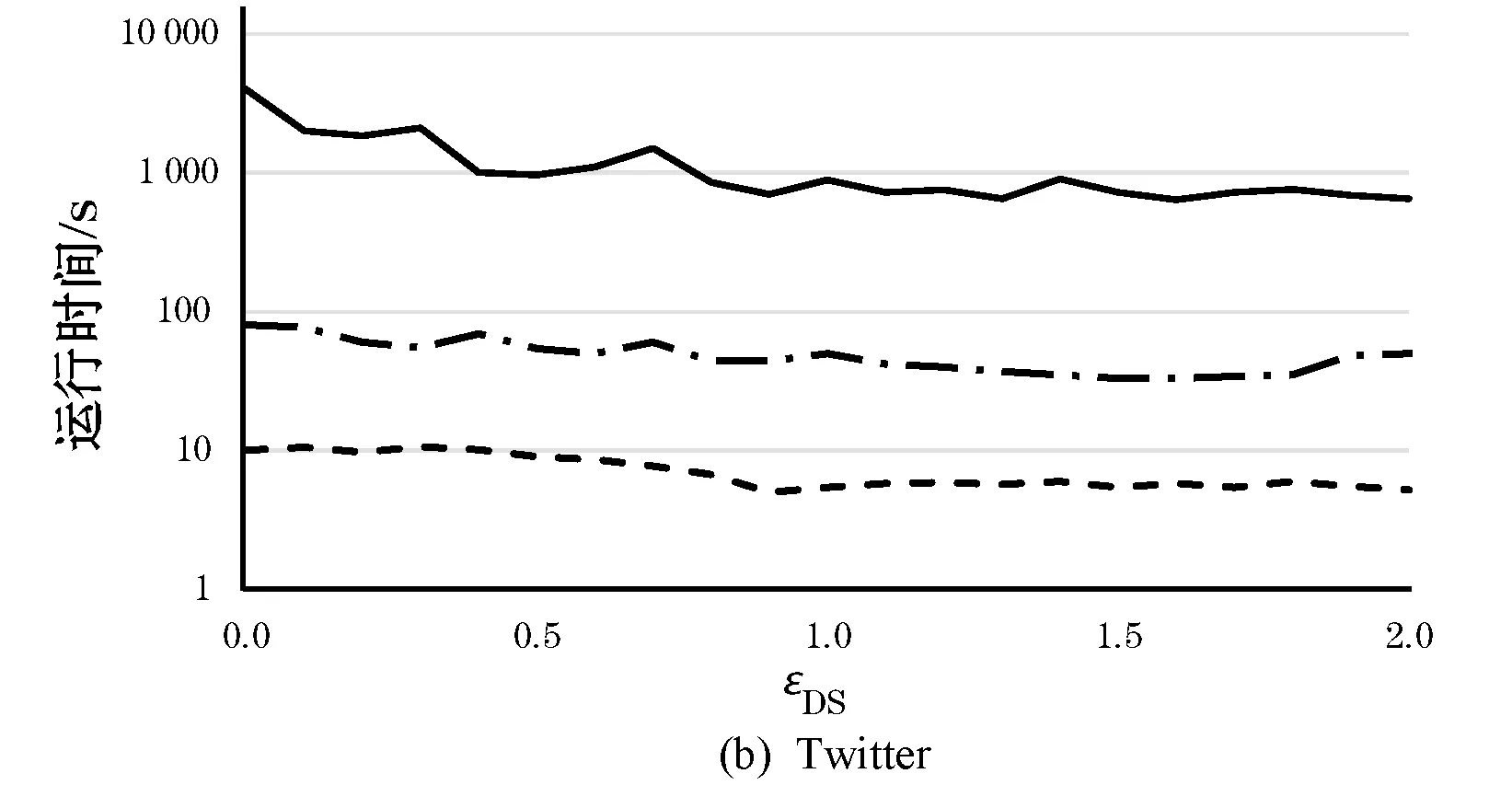
图4 不同近似参数对算法的影响
实验还使用不同大小的滑动时间窗执行算法,即x=10k,100k,1M,10M,实验中设置k=10,评估滑动时间窗大小对算法的影响,使用具有DFS排序的FacebookL和TwitterL数据集。表3给出不同大小滑动时间窗的运行时间。增大滑动时间窗不会显著地影响算法运行时间,这一结果表明大多数的更新都是子图局部更新,并不需要遍历整个图。
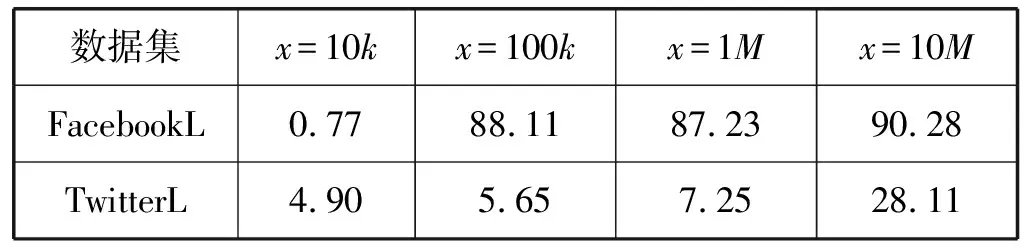
表3 不同大小的滑动时间窗对算法运行时间的影响 ms
图5是在Facebook和Twitter数据集中增加交互次数,运行时间的变化显示出算法的可扩展性。实际上,运行时间在前1 000次交互中快速增长,然后饱和到线性依赖,因为网络初期顶点数量增长比较快,而且可能出现比之前更稠密的子图,必须频繁计算近似稠密子图。图5表明区间k的数量对算法的运行时间也有影响,随着k的增加运行时间增加。
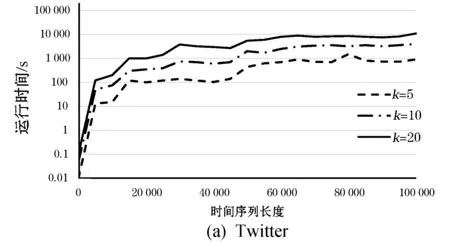

图5 算法的可扩展性
5 结 语
本文研究了在时态网络中基于滑动时间窗找到一系列稠密子图的问题,并提出一种有效的动态算法。现有算法在图更新时迭代整个图,本文算法仅影响图的有限区域,因此只需要局部更新稠密子图。结合滑动时间窗将网络时间线分割为k个非重叠间隔,使得间隔内能够发现具有最大密度的子图。结合理论分析,并验证该算法比文献[3]的算法更快。真实数据集上的实验验证本文算法是有效的,且可以得到高质量的结果。
今后的研究中,将考虑子图的频率、子图的统计非随机性对网络进行分割,另一种扩展是每个间隔内发现多个稠密子图可能是更有意义的。还可以考虑是否有可能在高度顶点的阈值上实现更强的界限,是否有可能为问题实现更好的近似保证,进一步改进算法,使其成为许多实际应用的有用工具。
