一种基于改进Kalman滤波的多传感器室内定位方案

唐 娴

(商丘学院计算机工程学院 河南 商丘 476000)

0 引 言

随着人们对位置服务需求越来越大，无论基于GPS还是基于北斗的室外定位服务均已在现实生活中被广泛应用。然而，每当人们进入到室内后就会发现定位精度逐渐降低，这是因为基于GPS或北斗的定位服务在室内受非视距和多径效应影响导致卫星信号衰减较大。因此，室内定位服务质量问题已成为新一轮研究趋势。移动手机是现代社会发展最快的产业，其感知前端具有多传感器融合、多媒体信息传输和存储等优点，可以直接利用移动手机中内置的惯性传感器[1]进行行人航位推算(Pedestrian dead reckoning,PDR)[2]，以此来实现较为精准的室内定位服务。

如果仅利用手机内置惯性传感器(主要包括加速度传感器、陀螺仪、方向传感器、磁力计等)进行定位推算，将易造成累积误差，会导致定位结果精度和可靠性偏低，所以需要将不同的定位技术进行融合来得到更高的定位精度。Li等[3]提出了将惯性传感器、Wi-Fi和地磁定位技术进行融合，除了需要在行人航位推算中消除累积误差，还需要考虑实际应用中室内人员的非步态干扰和手机设备的抖动等，使得采集的多种传感器信号易产生漂移和失真，即使PDR算法精度很高，也无法消除信号强度失真造成的定位误差，所以必须对采集到的信号进行滤波去噪处理。唐士凯等[4]利用单一的Kalman滤波对信号进行处理，然而这种滤波方法对信号波动明显的采样点效果不明显，也会制约Kalman滤波的收敛速度。

针对多传感器中信号易受室内复杂环境、人员非步态干扰及自身漂移影响，导致的定位精度低、实时性差和鲁棒性不强等问题，本文提出一种改进的Kalman滤波多传感器室内定位方案。方案的主要思想包括以下几点：(1) 由于GPS或北斗的定位服务在室内定位上误差较大，故本文利用智能手机中自带的方向传感器和加速度传感器可实现较精准的短距离室内定位服务。(2) 采用PDA算法实现行人室内定位，而该算法在计算行人位置前需先估算行人步伐长度和统计行人移动的步数，由于室内定位是短距离定位，采用常数模型即可满足步长估算需要。(3) 步数统计通常采用三轴加速度矢量和的方法计算，但是由于直流分量和随机噪声使得加速度的测量结果不准确(直流分量可以在系统初始化时对加速度传感器进行多次测量，然后再利用均值的方法预先加以矫正，所以加速度不准确的原因是随机噪声)，因此采用Kalman滤波消除随机噪声，原因是Kalman滤波具有最优化自回归数据处理算法的特点，可以有效消除人员扰动、信号多径效应等因素引起的信号噪声。(4) 考虑到Kalman滤波在噪声较大时会导致收敛速度变慢、数据稳定性变差等问题，因此在Kalman滤波的基础上结合均值滤波的方法进行改进，对干扰幅度较大、瞬时的脉冲信号具有较好的滤波消除效果。实验仿真说明，本文方案获得了更高的定位精度和鲁棒性更强的定位效果，对加速度处理、步数检测、定位精度及系统鲁棒性有一定的改善作用。

1 基于多传感器的PDA算法

多传感器融合的室内定位方法主要采用移动手机内置的方向传感器和加速度传感器来实现。其中：方向传感器为用户提供以正北方向为基准的磁偏角，能直接作为PDA的基本角度数据；加速度传感器能为用户提供实时的加速度数据并显示行人的运动状态。将两者信息经过PDA算法即可得到行人运动轨迹，其原理如图1所示。

图1 行人航位推算算法原理图

已知行人t0时刻的初始位置为(X0，Y0)，Ln表示tk时刻的步伐长度，θn表示tk时刻航向角，则tk时刻的位置为：

(1)

可见，直接影响室内定位PDA精度的主要因素有初始位置坐标、磁力计的航向数据、计步数据的准确性，以及可靠的步长估计模型。

1.1 行人步伐长度估计

由于人体的长时间内行为习惯及路面情况的多变性，造成了步长估计困难。通常行人步长估计模型主要有常数模型、线性模型和非线性模型三种。

(1) 常数模型：

L=A

(2)

通过预期对大量的已知长度的步伐进行测量，比较建模后得出一个在短距离估计下的步长平均值A。

(2) 线性模型：

L=a+bf+cv+γ

(3)

式中：a、b、c为通过训练求解得出的线性回归参数；f为当前的周期频率值；v为当前步伐加速度的方差；γ为高斯噪声[5]。但由于环境因素的干扰及智能手机系统存在一定的延误，会造成步伐频率和加速度统计量的误差和不规律性。

(3) 非线性模型：

(4)

式中：amax和amin分别表示三轴加速度的最大值和最小值；K为模型参量[6]，针对不同行人的不同环境情况建立不同非线性模型，其模型参量K值也不同。

由于采用变步长会增加算法时间复杂度，且所给方案主要研究滤波算法对多传感器融合的室内定位精度的提高，是在短距离内对行人信息的采集和定位，所以选用常数步长估计模型就能满足本文方案的步伐长度估计要求。选取10名成年志愿者对其在正常状态下多组步伐长度进行测量，得出步伐长度均在0.5～0.7 m之间，因此本文方案步伐长度取值为L=0.6 m。

1.2 步数统计

所给方案引入X、Y、Z三轴加速度参数来研究行人步数特征，通过计算三轴加速度矢量和的方法来进一步统计行人步数：

(5)

理论上，行人在静止情况下，手握手机设备进行数据获取，得到的三轴加速度矢量和应等于重力加速度g。但是在实际测量中，手机内置的多种传感器检测精度有限[7]，且存在行人非步态动作的干扰，在静止状态测得的加速度数据也会出现轻微的抖动现象，如图2所示。经多次测量得出加速度传感器采集X、Y、Z三轴方向上的加速度，其受非步态干扰的波动范围约为0.3 m/s2。为降低以上干扰数据的影响，PDA算法首先应对原始加速度数据进行预处理。

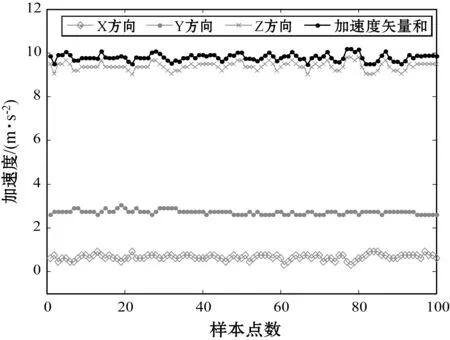
图2 静止状态下三轴加速度以及矢量和曲线图

1.3 基于阈值分级的步态检测

为了进一步统计行人步数，在运动过程中引入上述三轴加速度矢量和A，其值在重力加速度g附近上下波动且具有周期性。因此，所给方案采用设置上下阈值来确定加速度矢量和的波峰波谷。假定选取的上阈值为(g+f)、下阈值为(g-f)，对阈值上下值进行分级处理[7]：

(6)

式中：i为采样点个数；Ai表示第i个样本点经过预处理滤波后的加速度矢量和，其中g=9.8 m/s2；f=Ai-g∈[Amin,Amax]，即为加速度矢量和减去重力加速度，考虑到运动过程中非步态及其他运动动作的干扰，f取值为0.5[8]。

根据行人步伐特征，只有当连续检测到的状态为“波峰状态-过渡状态-波谷状态”时，才能将其判断为一个有效的步数周期，以此来统计行人的步数。

2 非步态特征下Kalman滤波器数据预测

针对多传感器在信息采集阶段易受行人非步态干扰的问题，直接采集加速度传感器数据而不做任何处理，即使在静止状态下也会出现跳跃不稳定或推挤现象，使得读取的数据波动明显、误差大且稳定性差，因此在采集阶段，利用Kalman滤波器对非步态特征下的数据进行最优预测，消除线性随机微分系统和测量过程产生的高斯白噪声。

2.1 Kalman滤波算法

Kalman滤波算法是一种线性最小方差估计，其主要过程包括预估与校正，以最小均方误差为最佳估计准则，建立信号和噪声状态空间模型，利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，求出当前时刻的估计值[9]，具有最优化自回归数据处理算法的特点。其思想流程如图3所示。

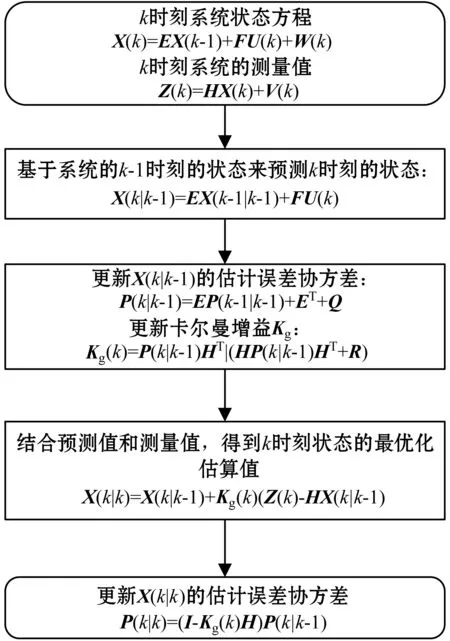
图3 Kalman滤波流程

图3中，E、F为系统参数；U(k)是k时刻对系统的控制量；Z(k)是k时刻的测量值；H是测量系统的参数；W(k)和V(k)分别表示过程和测量的噪声；Q和R分是过程噪声和观测噪声的协方差；U(k)为现在状态的控制量。

2.2 加速度数据采集经Kalman滤波器处理

由于加速度传感器的测量在实际环境中存在人员扰动及其他设备的干扰，使得加速度传感器读出的数值和真实加速度存在一定的偏差，其影响测量结果的因素主要包括直流分量和随机噪声，即：

A′=a+a′+n

(7)

式中：A′为测量加速度值；a为真实加速度值；a′为直流分量；n为随机噪声。在系统初始化时，对加速度传感器进行多次测量，利用均值的方法预先对直流分量加以矫正[10]。但由于随机噪声的不可测量性，无法采用多次实验进行预先矫正，所以所给方案采用Kalman滤波方法消除随机噪声，其过程建立如图4所示。

图4 加速度信号滤波流程

根据以上条件得到加速度信号采集系统状态模型如下：

(8)

(9)

同理可得Y轴和Z轴加速度信号采集系统状态模型为：

(10)

(11)

(12)

(13)

在实验室环境下，采用华为荣耀8X智能Android手机作为测试机，已知初始位置信息，打开采样App，其加速度传感器采样频率为100 Hz，行人步伐频率约为0.8 Hz。将手机平拿到距离地面1.2米左右高度按照预定路线匀速移动，实际行走步数为30步，对采集到的X、Y、Z三轴加速度进行Kalman滤波处理后，求取三轴加速度矢量和，再根据阈值分级的步态检测方法，得出经Kalman滤波处理后的行人步数值。其滤波结果如图5所示。

(a) Kalman滤波前后加速度矢量和对比

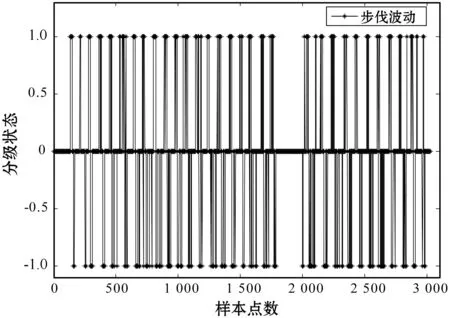
(b) Kalman滤波后的阈值分级图(步数统计为37步)图5 Kalman滤波处理前后效果图

未经Kalman滤波处理前的加速度矢量和噪声波动大，经阈值分级步态检测方法得到步数统计值为48步，与实际行走步数值相差较大。

由图5可知，将Kalman滤波应用在多传感信号处理上，可以有效滤除由于人员扰动、信号多径效应等因素引起的信号噪声，其步数统计值为37步，提高了步数检测精度。但在加速度数据噪声过大时，其收敛速度变慢，且数据稳定性也较差。

2.3 改进的Kalman滤波器应用于实时信号采集

上述算法单独使用Kalman滤波处理加速度，对于数据输出波动明显的采集点，在环境干扰下产生的噪声较大时会直接减慢Kalman滤波的收敛速度，使数据稳定性变差[11]。所以，结合系统响应速度及滤波效果，将滤波算法作改进，结合均值滤波对干扰幅度较大、瞬时的脉冲信号具有较好的消除效果。采用多次滤波算法作为加速度数据的预处理，以均值滤波中连续N次采集数据为一组，进行一次滤波，将滤波结果作为Kalman滤波的输入量，进行二次滤波，得到稳定性、可靠性、实时性更好的滤波效果。

经典均值滤波基本原理如下：

(14)

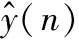
该算法针对连续采样得到的数据，首先定义一个固定长度为M的观察窗，每次将新采集到的样本点数据放入队首，并将队尾的数据删除，计算观察窗中最新的M个数据的平均值作为滤波后的结果，其基本工作原理如图6所示。

图6 均值滤波器基本原理图

在多传感器信号采集阶段，考虑到滤波效果和算法对内存的消耗会影响运行时间，因此对加速度传感器测得的X、Y、Z三轴加速度分别取M=10、M=15和M=20做均值滤波处理，以均值滤波处理后的数据作为一次测量值再利用Kalman滤波进行递归运算，求取出三轴加速度矢量和及行人步数值。其实验结果如图7所示。

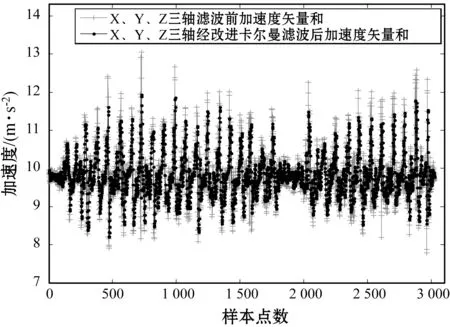
(a) M=10时，步数检测为31，运行时间为2.397 670 s

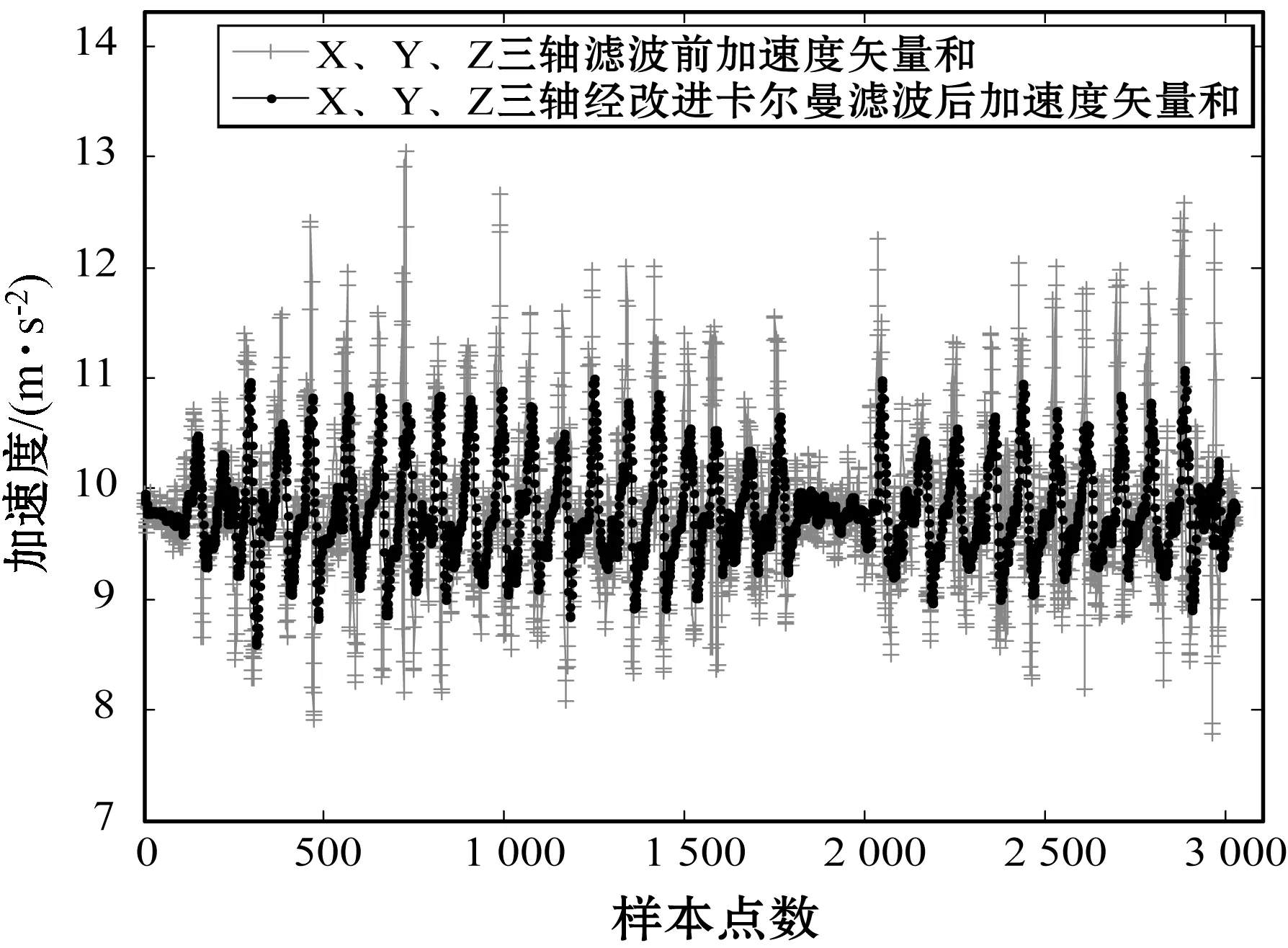
(b) M=15时，步数检测为30，运行时间为2.404 433 s

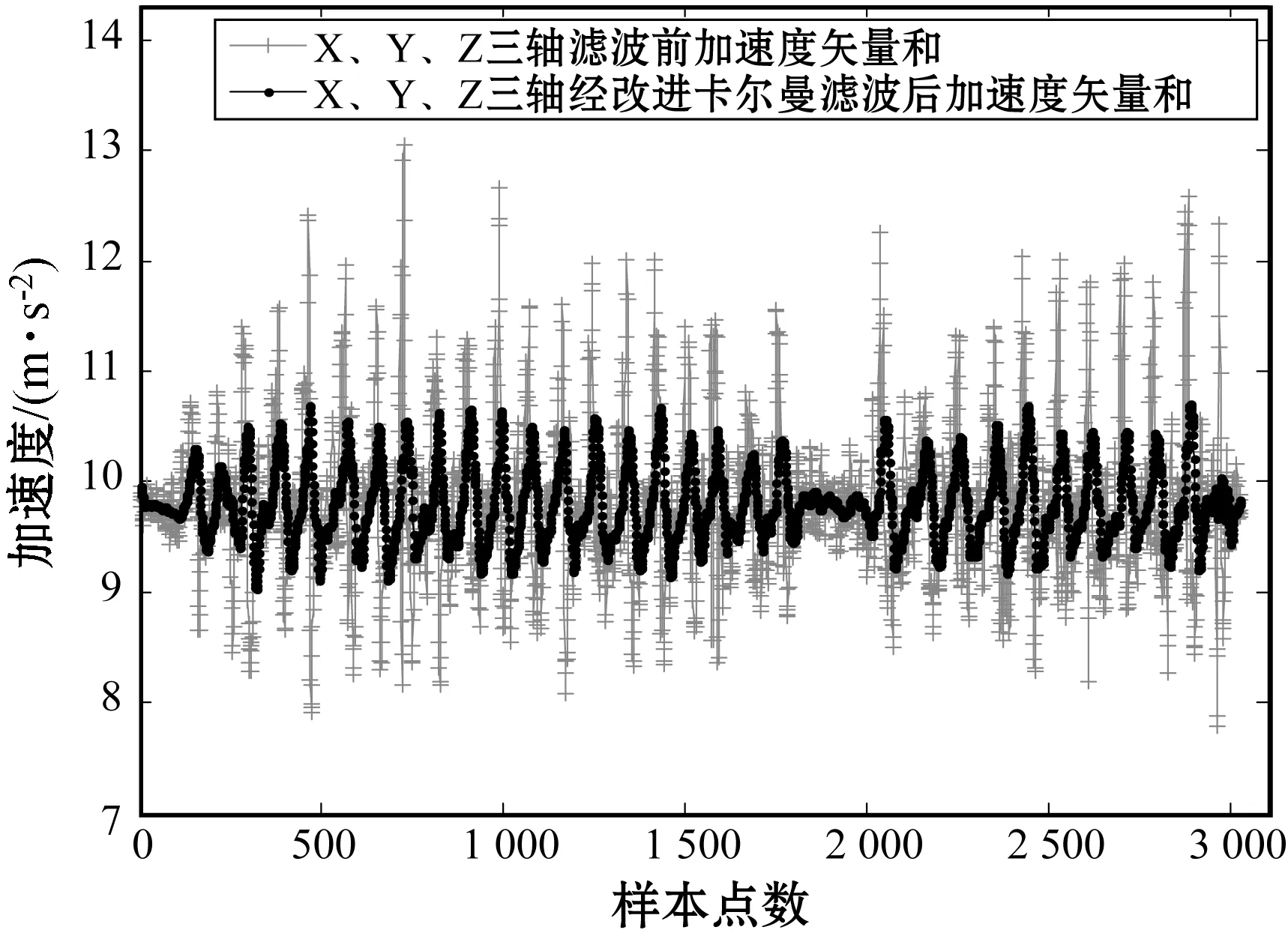
(c) M=20时，步数检测为24，运行时间为2.411 707 s图7 不同M取值下的加速度矢量和及步数检测值

对比图7(a)-图7(c)可知，当M取10～20时，随着M增大，滤波算法对加速度结果的优化效果越明显，但当M取20时，会丢失掉有用的加速度数据。因此，结合滤波效果、步数检测结果及运行时间，当M取15时，其滤波效果优于单独使用Kalman滤波，并且得到的步数检测值为28步，与实际步数值更加接近。综上，采用均值滤波+Kalman滤波对加速度数据处理，可以有效抑制信号干扰，提高相应速度，降低平均运行时间，提高步数检测精度，并为实时定位提供更为稳定、平滑的数据值。

根据上述改进Kalman滤波处理，得到优化后的多传感器室内定位流程[12]如图8所示。

图8 多传感器室内定位流程

3 实 验

3.1 实验环境布置

实验区域选用10 m×36 m的办公区域，其环境平面如图9所示，包括办公室和走廊，室内环境复杂度较高。为加大实验数据，增加路径二进行数据分析，实际行走步数为30步，其中黑色线路代表路径一，灰色线路代表路径二。

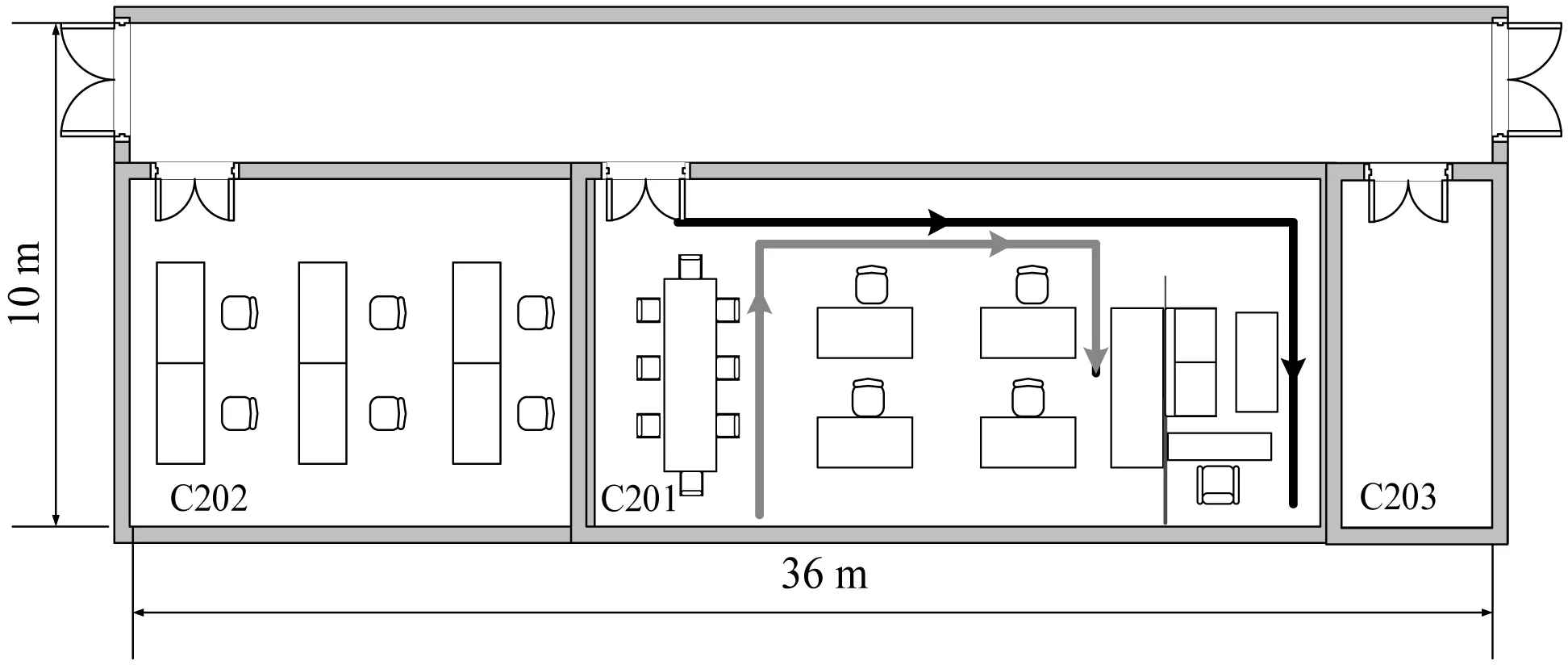
图9 实验环境平面图

3.2 仿真实验结果及分析

改进Kalman滤波对路径一和路径二的加速度信号做处理，得到优化后的传感器数据，进行行人航位推算，得到路径实验结果对比图，如图10所示。

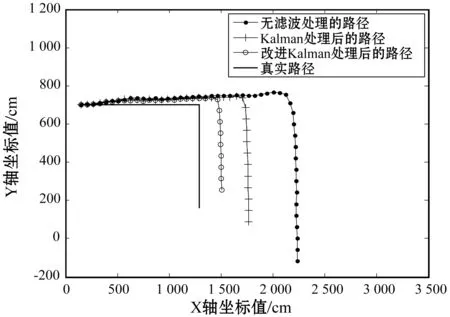
(a) 路径一

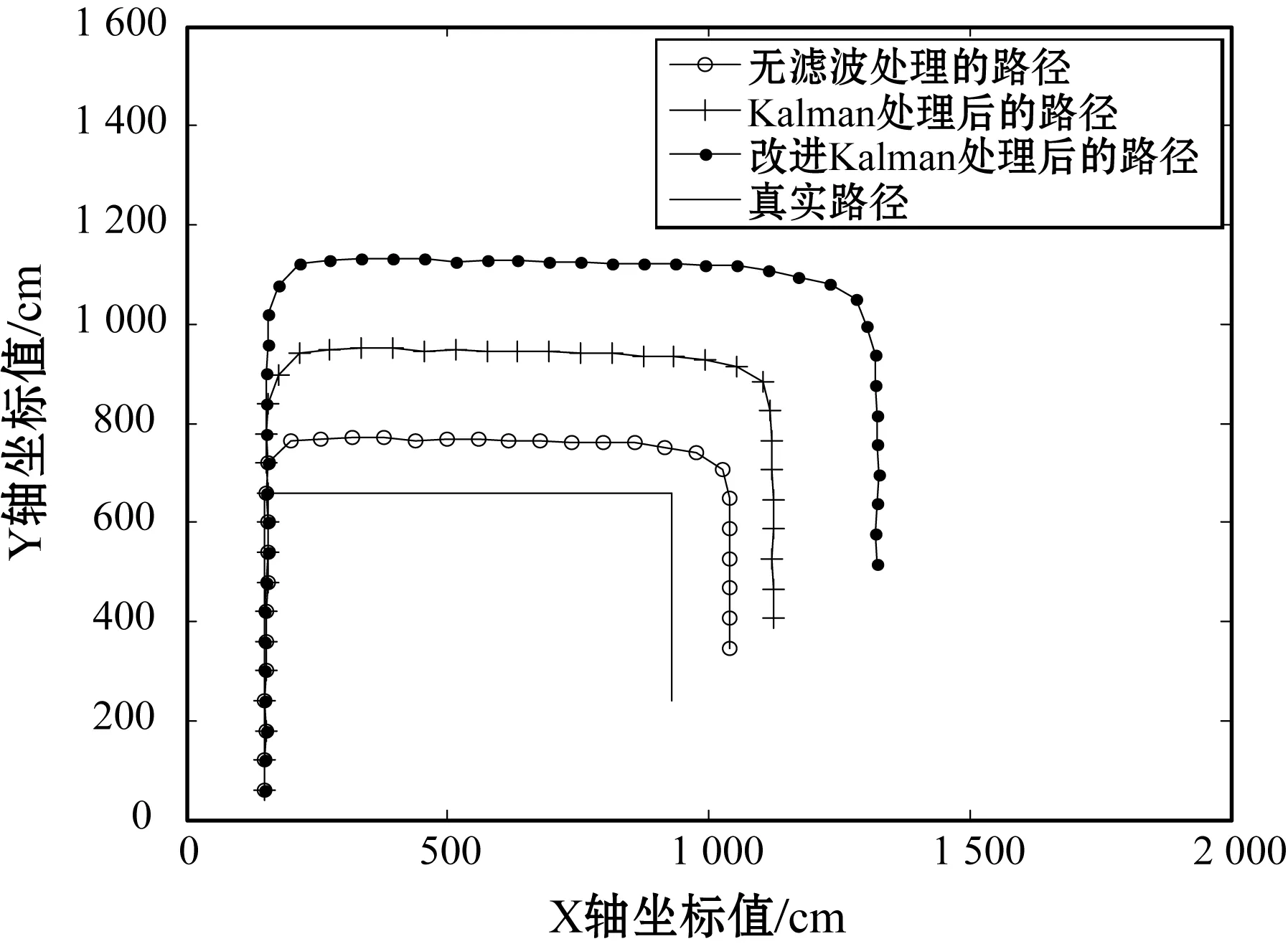
(b) 路径二图10 不同滤波处理下的路径结果对比图

在行人非步态干扰和传感器自身测量漂移下，改进的Kalman滤波对加速度处理后得到的定位路径相比于单一的Kalman滤波处理更加贴近真实路径，且步数检测也更加接近真实值。不同滤波处理下的位置误差累积概率如图11所示。

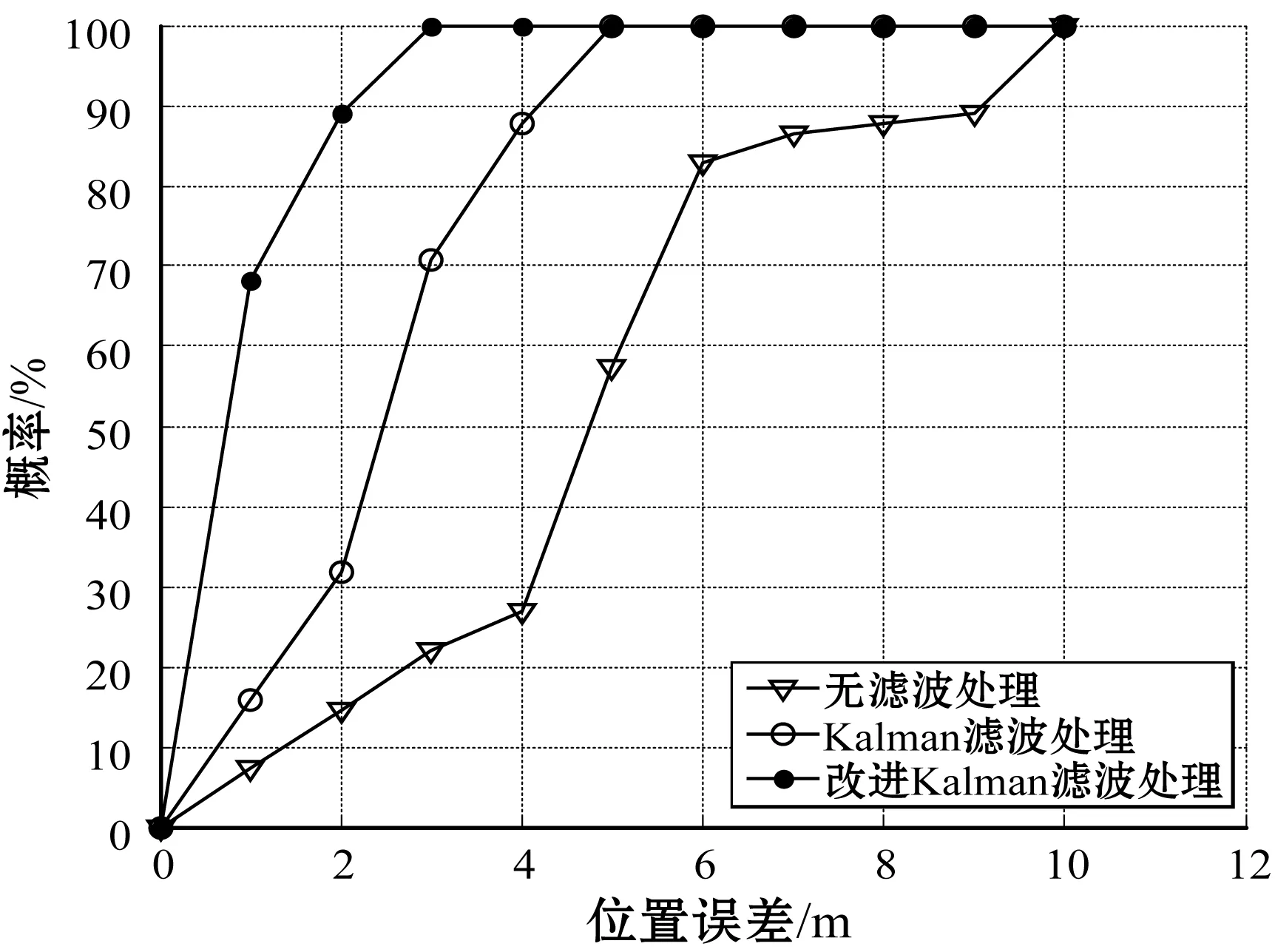
图11 不同滤波处理下的位置误差累积概率

可以看出，在本次定位处理中，无滤波处理的定位精度较低，在短距离4 m内的定位精度只有26.8%；在经过Kalman滤波处理后，3 m内的定位精度可以达到70.7%，但在2 m内的定位精度只有31.7%；为此，以均值滤波处理后的数据作为一次测量值再利用Kalman滤波进行递归运算，其定位精度在2 m内达到了89%，1 m内也能达到68.2%。

3.3 真实实验结果及分析

Android手机端实时采集信号及定位结果如图12所示。

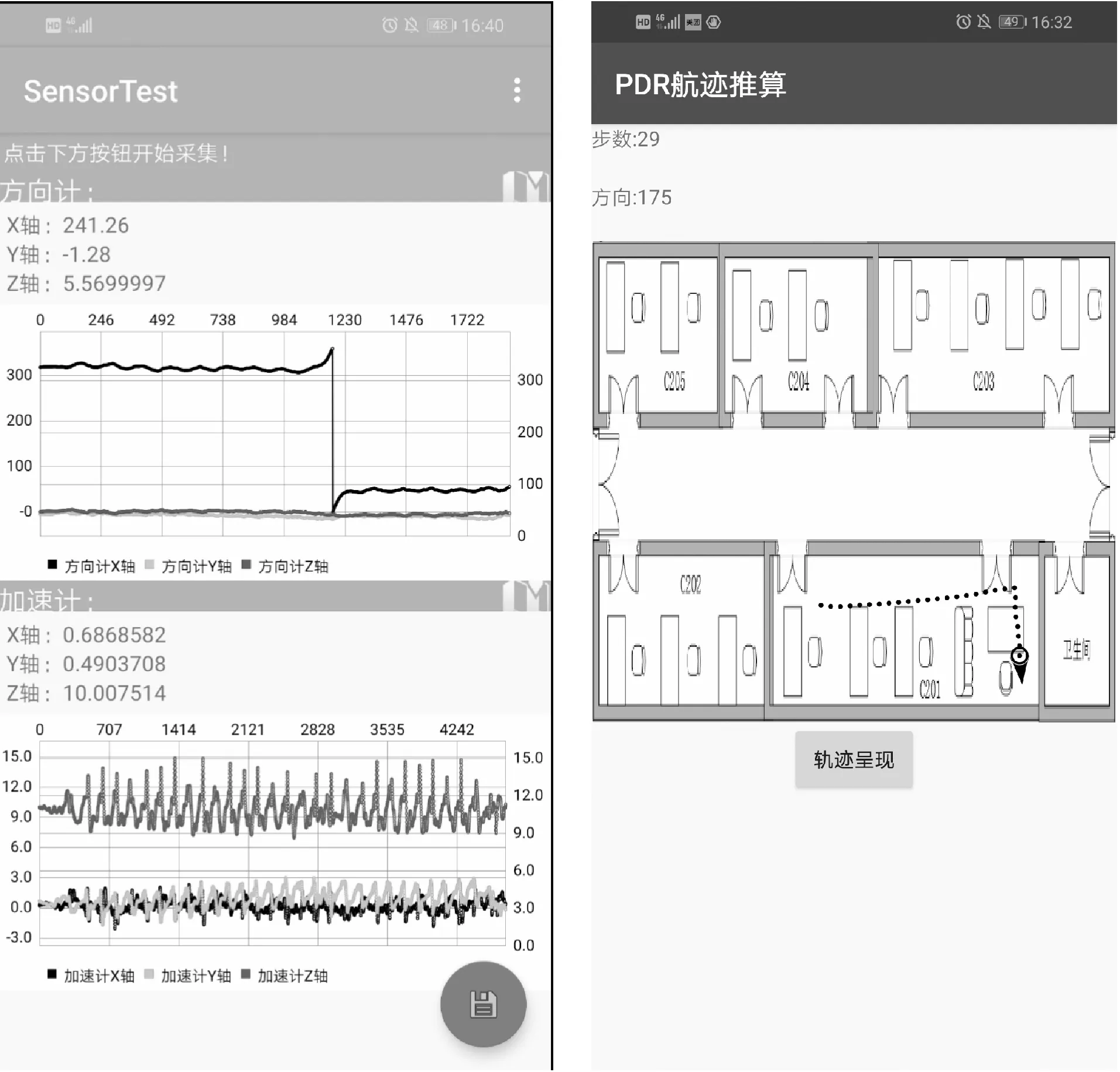
(a) 实时信号结果图 (b)实时定位结果图图12 Android端信号采集及定位结果示意图

将路径一和路径二总的采样点作滤波处理，得到多个待测点进行平均定位误差、误差标准差计算，比较定位精度与实时性效果，结果如表1所示。

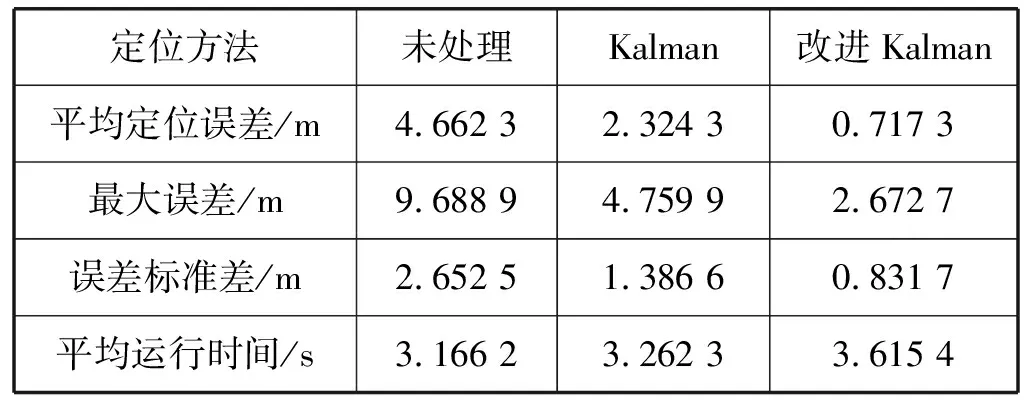
表1 几种滤波算法定位精度与实时性的比较

对表1分析可得，改进的Kalman滤波相对于无滤波处理和Kalman滤波，在平均定位精度方面分别提高了84.61%、69.14%；定位最大误差也在减小，同时定位稳定性也随着滤波处理方法的改进而增强。但由于改进滤波处理方法的复杂性和多样性，平均运行时间会有所增加，因此会牺牲一部分运算速度，获得定位精度更高、鲁棒性更强的定位效果。实验结果表明改进的Kalman滤波算法对加速度处理、步数检测、定位精度及系统鲁棒性有一定的改善作用。

4 结 语

针对多传感器中信号易受室内复杂环境、人员非步态干扰及自身漂移的影响，本文给出了一种改进的Kalman滤波多传感器室内定位方案。实验结果表明，本文滤波算法相较于Kalman滤波算法，在2 m内的定位精度由31.7%提高到了89%，其平均定位精度提高了69.14%，同时运行稳定性也有所加强，但多传感器信息融合定位在长时间的定位过程中，会出现累积误差，所以未来可以针对累积误差进行多种定位方法的融合，进一步提高定位精度和稳定性。