基于双层规划的多供应商物料配送期量优化
2021-07-16郑广珠杨晓英张瑞敏王金宇
郑广珠 杨晓英 张瑞敏 王金宇
(河南科技大学机电工程学院 河南 洛阳 471003)
0 引 言
为了快速响应多样化和个性化的客户需求,制造商逐步采取多品种、小批量生产模式。制造商在满足客户多品种多规格的产品需求时,其生产需求也是复杂多变的,供应商进行准时化配送物料的难度也随之增加。为减少自身库存和配送成本,供应商采取大批量低频次的配送方式将物料提前运送到制造商仓库。但是制造商仓库空间有限,零部件却是成千上万,导致库存积压甚至出现“爆仓”的情况,同时供应商配送时间集中且无序导致制造商处卸货拥堵、卸货效率低等问题。因此,为了提高供应商配送效率,降低物流成本,进行供应商配送期量标准研究具有理论与实际意义。
国内外学者已经对供应商配送问题进行了深入研究。文献[1-2]通过建立运输与库存协调优化模型,达到供应链系统总利润最大化的目标。文献[3-4]研究了单一制造商和多个销售商的联合运输策略。文献[5-6]研究了制造商和第三方物流服务提供商的生产和物流的综合优化问题。赫超等[7]通过建立混合整数规划模型求解供应链网络调度问题。文献[8-9]探讨了在集配中心运作模式下,制造商最佳订购策略以及供应商配送协同优化策略,并确定了供应商的最佳配送批量和补货次数。吕飞等[10]分析了成本信息不对称情况下制造商对多供应商采取价格补贴方式能够保证在供应链成本降低的条件下协同配送。文献[11-12]建立以配送成本和库存成本最小化为优化目标的数学规划模型,并提出基于物联网的动态物料配送方案。文献[13-14]通过建立物料的最佳配送时间和数量区间,设计动态配送策略,以达到降低生产调整成本的目的。戢守峰等[15]为减小供应链总库存成本,深入研究了多个供应商之间如何利用横向协同齐套向制造商供应物料问题。
综上所述,这些研究侧重于考虑单供应商或多供应商配送单种物料情况下配送批量的确定,但是针对多供应商配送多种物料并与产品生产顺序计划协同的物料配送期量标准研究较少。本文以每日物料需求计划为供应商配送基础,以生产计划为驱动,以供应链总成本最低为优化目标,综合考虑物料需求时间以及供应商配送能力等约束,建立多供应商配送期量标准的双层规划模型,采用遗传算法与动态规划法相结合的方法进行模型求解,确定各供应商的配送期量标准,有效提高供应商物料配送的协同性和准时性。
1 问题描述
多品种小批量式生产产品种类多、物料变更频繁,制造商根据生产计划以及产品BOM确定匹配采购订单。为保障物料的充分供应,每个供应商按比例供应多种物料,同种物料也可由多个供应商进行配送。制造商排产后,及时将其生产顺序计划信息与每个供应商共享,来提高供应商配送的准确性与准时性。供应商为满足制造商生产需求并降低配送成本,会采取大批量少频次配送,产生了制造商库存浪费并增加了仓库管理难度。此外,各个供应商根据制造商使用的时间自主确定配送时间,不同供应商会集中在同一时间段到达卸货处,由于制造商的卸货能力有限,供应商需要在仓库门口排队等待,这种配送方式不仅影响供应商的配送效率,而且会由于卸货不及时影响生产线的顺利运行。
为解决以上问题,本文提出一种供应商协同配送策略。该策略是根据制造商日生产计划和库存能力确定每个供应商单次配送量和配送次数,并根据物料的需求时间和供应商运输时间确定各个供应商的配送时间序列,将正确的物料在正确的时间配送至制造商处。
2 多供应商配送期量标准双层规划模型
根据制造商每日生产计划需求,确定各供应商的订单需求量及需求时间,考虑供应商配送成本、制造商储存成本及卸货能力约束,满足制造商时间生产需求,建立多供应商配送期量(批量-时间)的双层规划模型。
2.1 模型假设与符号描述
模型假设:
(1) 一种物料由多个供应商供应,一个供应商供应多种零部件;
(2) 供应商配送的前提是生产计划确定,按规定需求进行配送;
(3) 物料的采购清单已经确定,不涉及突发物料需求;
(4) 供应商不允许出现缺货。
参数说明:
i表示物料编号,i=1,2,…,n;
S表示供应商编号,S=1,2,…,m;
qiS表示物料i由供应商S的单次配送量;
αiS表示不同供应商配送次数;
cdS表示供应商S的单次配送成本;
ch表示制造商的单位库存维持成本;
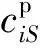
QdS表示供应商S的单次最大装载量;
QiS表示供应商S的物料i总需求量;
Li表示制造商仓库的最大存储量;
r表示制造商生产节拍;
λiS表示物料的单机使用比例;
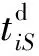
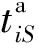
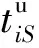
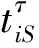
βiS表示单个供应商卸货需要的工具数量;
F表示制造商叉车总量。
2.2 模型建立
(1) 上层模型:供应商配送批量优化模型。以供应链物流总成本TC最低为目标,考虑供应商的配送能力和制造商的库存能力,建立供应商配送批量优化模型,确定供应商在满足生产需求下的最优单次配送量及配送频次。供应商由于配送成本限制,当需求量不足最优配送量时,按最优配送量进行配送,因此供应商每日物料配送总量不低于生产需求量。
min
(1)
s.t.
0≤qiS≤QdS
(2)
0≤qiS≤Li
(3)
αiSqiS≥QiS
(4)
(5)
式(1)为使供应链物流总成本最低的目标函数,主要由制造商库存成本和供应商配送成本两部分构成。式(2)保证单次配送量不能超过供应商车辆最大运载量,式(3)保证供应商单次配送量满足制造商仓库最大容纳量约束,式(4)和式(5)保证供应商单次配送量满足总需求与配送周期内的物料消耗。
(2) 下层模型:供应商配送时间序列模型。由于车间生产对物料到达时间也有限制,下层模型以供应商时间惩罚成本最低为优化目标,根据上层模型确定供应商的最优配送批量,考虑制造商的卸货能力以及需求时间对供应商到达时间进行排序,确定每个供应商配送时间序列,保证供应商有序到达。
min
(6)
s.t.
(7)
(8)
(9)
式(6)为使供应商时间惩罚成本最小的目标函数。式(7)保证制造商的卸货能力,式(8)和式(9)为供应商的到达时间限制。
3 模型求解
本文研究的问题主要由配送批量和次数、配送时间两个部分组成,关键的问题是确定供应商的单次配送批量。采用遗传算法求解供应商的最优配送批量和配送次数,运用动态规划法解决各供应商的到达时间问题[16]。整个模型的解决流程如图1所示。

图1 算法流程
3.1 遗传算法求解配送批量
(1) 编码。编码是遗传算法要解决的首要问题,通过对上述模型分析,可以将物料、配送量、供应商作为染色体,用染色体表征供应商配送方案,采用矩阵形式表示个体染色体[17]。每种物料都需要由指定供应商配送,可以用3×n的矩阵M形式。基于此,本文的染色体可用矩阵表示为:
式中:i表示物料编号;qiS表示各供应商单次配送量;S表示供应商编号。M表示供应商2负责物料1每次配送量为q1,供应商3负责物料2单次配送量为q2,供应商m负责物料n单次配送量为qn。
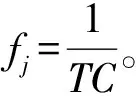
(3) 选择操作。选择操作的目的是从群体中选取最优个体,使适应度值高的个体有更大的生存概率。本文采用轮盘赌的方式进行选择,假设种群数量为N,选择过程为旋转轮盘N次,每次为种群选出一个个体,各个体被选中的概率与适应度值成正比,选择概率可表示为:
(4) 交叉操作。交叉操作时在选择得到的种群中两个染色体按照某种指定方式互相交换其部分基因形成新个体,以保证个体的完整性和多样性。以概率Pc随机交换染色体群中两个个体的某些片段从而生成新个体,对于矩阵形式的染色体一般定义交叉矩阵的某些行或列产生新个体。交叉概率Pc一般取0.25~1.00,本文Pc=0.8。
(5) 变异操作。变异主要有两个作用,一是利用变异运算使GA具有局部随机搜索功能,加快算法的收敛速度;二是可以通过变异运算中新个体的产生来增加种群的多样性。变异概率Pm一般取0.000 1~0.1,这里Pm=0.01。
3.2 动态规划法求解配送时间序列
该问题可以简化为对已知的单次配送量qiS和配送次数αiS,根据制造商的物料需求时间区间求解供应商的配送时间序列。每个供应商配送相互独立,可在同一时刻安排配送,在卸货能力满足的情况下,制造商可同时对多个供应商卸货。设N为满足约束条件的所有的供应商配送时间序列,X为其中任一排序,最优排序的目标函数为:
f(X)=minZ
Step1根据物料最早需求时间和已知的单次配送量qis和配送次数αis,规划供应商每次配送最晚到达时间序列。
Step2根据供应商运输能力、制造商卸货能力和最晚到达时间约束,用动态规划法划分批次,并对所有批次的配送时间进行排序。
Step3找出所有满足约束式(7)-式(9)的排序集合。
Step4计算每一种排序集合X的f(X)。
Step5根据所求最小的f(X)所对应的排序集合即为最优配送时间序列。
4 实例验证及分析
4.1 实例数据
以某农机制造企业拖拉机装配车间为例来验证上述模型和算法的有效性。该拖拉机制造企业机型种类繁多,具有高达上万种物料,涉及500多家供应商,为确保物料的供应保障能力,每种物料由多家供应商按比例进行供货。该装配车间采用混流装配生产模式,各物料在不同的时间生产需求不同,每种物料的需求时间和需求数量必须满足车间内动态变化的生产需求。本案例根据车间实际生产情况,选取其中6种关键物料进行验证研究,这6种物料由7家供应商供货。车间日生产计划装配总量为160台,生产节拍为3 min/台,每天工作8小时,由生产计划可得物料需求时间及对应批量如表1所示,供应商单位配送成本以及最大装载量等物料信息及参数设置如表2所示。
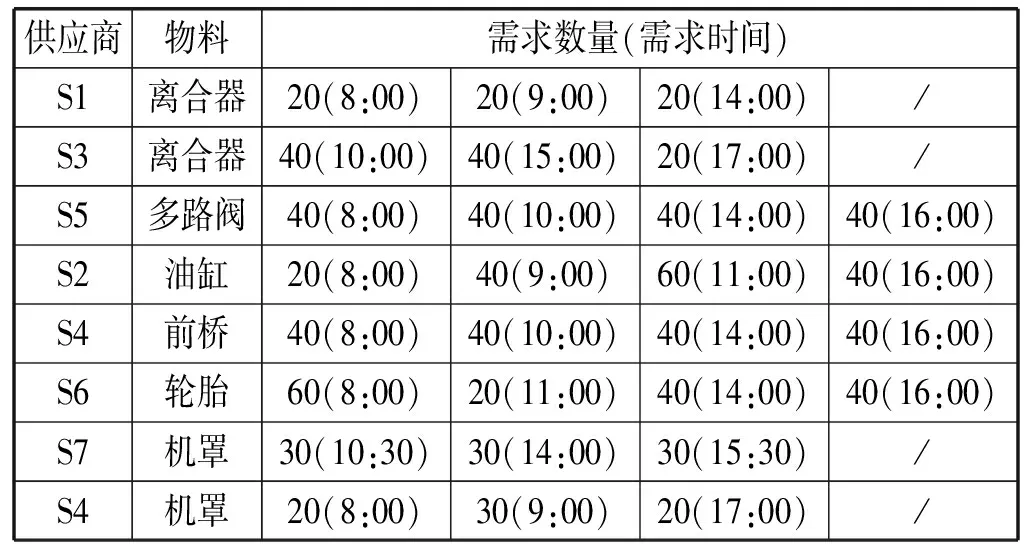
表1 物料需求时间表
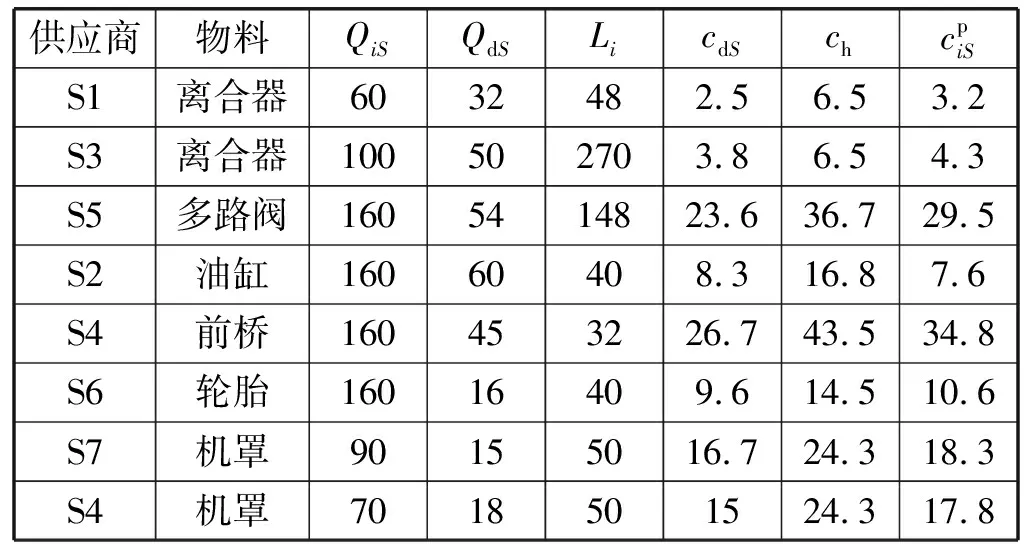
表2 基础物料信息及参数设置
4.2 算法应用及效果分析
通过MATLAB实现上述遗传算法,基本参数设置如下:种群规模为50,最大迭代次数为100次,交叉概率Pc=0.8,变异概率Pm=0.01。通过遗传算法运行5次,得到目标函数收敛过程如图2所示。
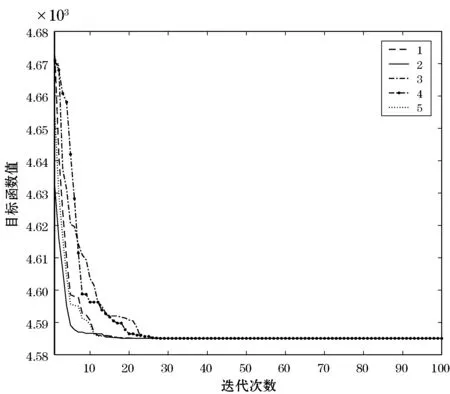
图2 遗传算法收敛过程
可以看出,每次计算种群在23代左右收敛至最优解,求解过程平稳,收敛速度快,验证了算法的有效性。利用遗传算法可得优化后各供应商的最优配送批量和配送次数,结合物料需求时间运用动态规划法确定各配送批次的时间序列,可得到优化后满足车间生产需求和约束条件下供应链物流总成本最低的各供应商物料配送期量,如表3所示。可以看出,供应商每批次配送时间都在需求时间之前,保证了制造商的生产需求,确定了供应商配送时间序列。对比分析优化前后各供应商的单次配送量与配送次数,如表4所示。可以看出,优化前各供应商单次配送量大多为运输车辆的满载量,配送批量缺乏经济性,优化后配送次数增加,单次配送量减少。

表3 优化后供应商物料配送期量(批量,时间)表
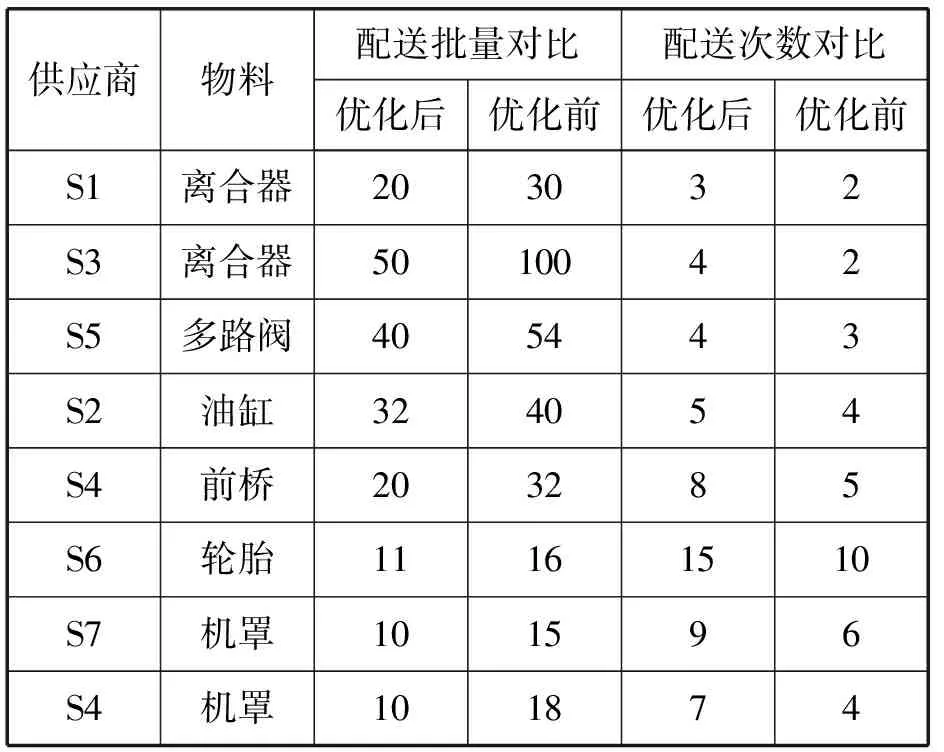
表4 优化前后供应商配送批量对比分析
为验证模型和算法的有效性,对比分析优化前后各供应商物流成本变化,如表5所示。从表5可知,优化后各供应商物流成本均与优化前相比均有所降低,供应链物流总成本从优化前的6 106元降低至优化后的4 585.1元,供应链物流总成本降低了24.9%,实现配送成本及库存成本的最优化。本算例说明该模型能够根据制造商生产需求确定供应商配送期量标准,避免供应商大批量配送现象,解决供应商协同配送问题,有效降低了供应链物流总成本,验证了该模型和算法的有效性及可行性。
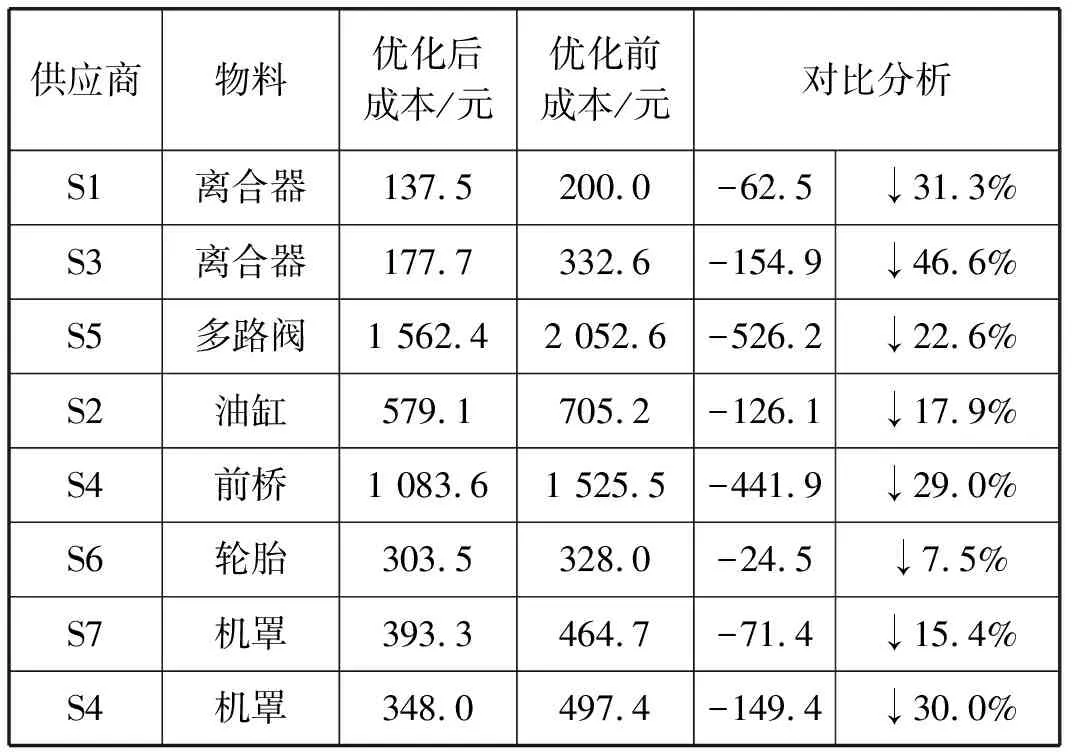
表5 优化前后各供应商物流成本对比分析
5 结 语
本文针对供应链中多供应商配送缺乏物料配送期量标准问题,研究既考虑经济配送批量又考虑供应商配送时间要求的供应商配送策略,建立基于双层规划的配送期量标准模型。以供应链物流总成本最小为目标建立上层配送批量优化模型,采用遗传算法进行求解,确定了供应商最优配送批量,能有效降低物流成本。以供应商时间惩罚成本最小为目标建立的下层配送时间序列模型,考虑了生产需求的时序性,利用动态规划法求解得到供应商最优配送时间序列,使每个供应商按需按序配送,提高物流转运效率。通过实例应用验证了双层规划模型及求解算法的有效性及可行性,为企业实现供应商精益化及准时化配送提供了理论依据。
