单点悬挂式结构物水动力性能和结构强度分析

张 涵，扈 喆，林国珍，张晓莹

（集美大学 轮机工程学院，福建 厦门 361021）

0 引 言

随着我国“建设海洋强国”战略的加速推进，海洋资源的开发和利用受到越来越多人的关注，海洋结构物设计概念越来越丰富。悬挂式海洋结构物是近年来兴起的海洋结构物，由底部压载舱和上方结构物主体组成，两者采用铰接方式连接。在工作状态下，上方结构物主体在压载舱向下的拉力的作用下沉入海底，而上方结构物主体在正浮力的作用下形成张紧式的“倒悬挂”结构。此类结构物具有成本低、抗风浪能力强和升降操纵方便等优点，可应用于海底环境监测等领域中。

由于悬挂式结构物通常需长时间在海上作业，故保证其具有良好的抗风浪性能和结构强度尤为重要。目前工程上常采用三维势流理论分析船舶和浮式结构物的水动力性能。例如：王红芳基于三维势流理论对某船舶波浪载荷进行了长期预报；韩旭亮等基于时域三维势流理论建立了波浪中多浮体作业系统耦合运动数学模型，计算了运输船靠近Spar平台安装作业时的运动响应；青兆熹等基于频域三维线性势流理论计算了浮式生产储油卸油装置（Float Production Storage and Offloading, FPSO）在规则波中压载、半载和满载工况下的响应幅值算子，并对其运动、加速度和剖面关键载荷进行了短期预报；ZHU等采用三维频域势流理论研究了各体间隙对多体浮式结构物波浪载荷的影响；KIM等基于时域三维势流理论，采用Rankine源方法计算了相邻多体结构物的运动响应。目前业界已对船舶和常规海洋结构物的水动力性能开展大量研究，积累了丰富的经验，但对单点悬挂式海洋结构物的水动力性能开展的研究不多。

本文以某单点悬挂式海洋结构物为例，建立其水动力模型和结构有限元模型，采用基于面元法的三维频域势流理论和小尺度构件Morison理论分析其水动力性能。在浮体运动矩阵方程中增加附加刚度矩阵项，模拟悬挂点的约束作用。将计算得到的波浪载荷、结构物运动惯性力和悬挂点约束力施加在有限元模型上，同时考虑重力和浮力的作用，计算该结构物的强度。

1 基本理论

1.1 频域三维势流理论

设流体无旋、无黏、不可压缩，浮体无航速，则速度势可分解为

式(1)中：

ϕ

为入射势；

ϕ

为绕射势；

ϕ

为第

j

个自由度单位幅值运动产生的辐射势；

η

为第

j

个自由度对应的运动幅值；i为虚数单位；

ω

为圆频率。对于单色微幅波，

ϕ

给定，

ϕ

和

jϕ

满足控制方程

式(2)中：

h

为水深；

k

为波数；

n

为第

j

个自由度运动对应的物面广义法向分量。采用Green函数法求解式(2)，得到流场压力，并将其代入浮体六自由度运动方程中，得

式(3)中：

M

和

M

为浮体质量矩阵和附加质量矩阵；

X

为浮体运动的广义位移；

C

为附加阻尼矩阵；

K

为静水回复力刚度矩阵；

F

为Froude-Krylov力与绕射力合成的波浪力；

F

为其他外力。

1.2 Morison理论

势流理论在求解大型结构的运动时效果较好，小尺度构件一般采用Morison理论计算，计算式为

式(4)中：

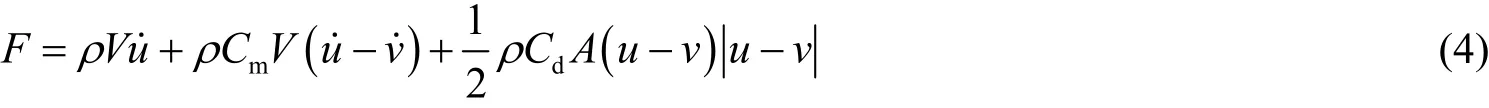
ρ

为流体密度；

V

为杆微元体积；

u

和

u

˙分别为流体的速度和加速度；

v

和

v

˙分别为杆微元的速度和加速度；

C

为附加质量系数；

C

为阻力（拖曳力）系数；

A

为杆微元的迎流面积。对于圆柱形管件，取

C

＝1。规范建议阻力系数

C

的取值范围为0.6～1.2。由于该平台管件的Reynold数大于5×10，故采用文献[7]的建议，取

C

=0.7。

1.3 悬挂点约束

图1为单点悬挂式结构物示意，其主体在悬挂点处有受到外力的作用，故须在控制方程中施加外力项。一般可采用2种方式处理悬挂点约束：

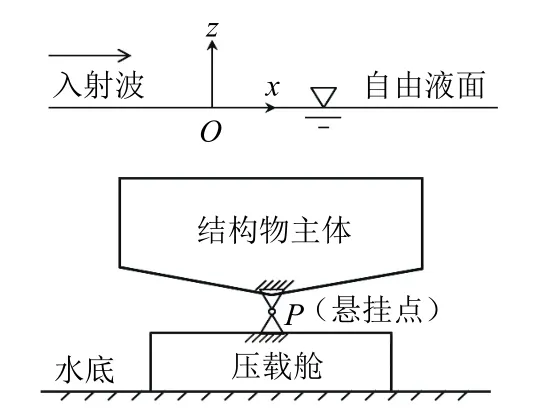
图1 单点悬挂式结构物示意

1) 在方程中施加外力，对于铰接式悬挂点，应施加3个方向的外力，同时增加3个约束方程，使悬挂点3个方向的位移为0；

2) 用刚度较大的弹簧代替悬挂点约束，在方程中添加附加刚度矩阵。

由于第1种方法增加了自由度个数，且不利于统一形式求解，故这里采用第2种方法模拟悬挂点的约束作用。

设

P

点为悬挂点，坐标为(

x

,

y

,

z

)，则悬挂点约束刚度矩阵为

式(5)～式(7)中：

k

、

k

和

k

为等效弹簧在3个方向上的刚度；

K

为弹簧局部刚度矩阵；

T

为坐标转化矩阵。

2 计算模型

该单点悬挂式结构物主要由梁柱框架、环形舱和底部压载舱等3部分组成，其中底部压载舱在建模时不予考虑。建模时环形舱采用面元（对应势流理论计算），梁柱框架采用梁元（对应Morison理论）。材料为Q345钢，弹性模量为210000MPa，波松比为0.3，密度为7850kg/m。若不考虑安全系数，则Von Mises组合应力的许用值为屈服极限，即345MPa，最大许用剪应力为230MPa。

有限元模型约束条件见图2，其中：悬挂点

P

设为

xyz

方向线位移约束；在底部环形框架周围取4个点（

A

、

B

、

C

和

D

），设为

yz

方向线位移约束。计算结果表明，约束点无显著的应力集中。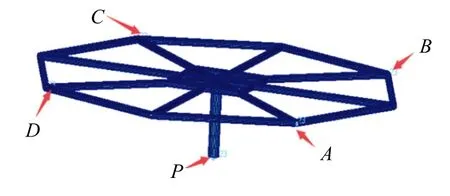

图2 有限元模型约束条件

参考规范的要求，结合该结构物的对称性，在进行水动力分析时浪向取0°和22.5°，波浪频率取0.2～1.8rad/s，间隔0.05rad/s，水深20m。采用软件SESAM.HydroD计算水动力性能，得到相关载荷，导入软件SESAM.Sestra中计算结构强度。在进行强度分析时，同时考虑静水载荷、波浪载荷和惯性力的作用，其中设计波幅取5m。

3 计算结果与分析

3.1 悬挂点载荷

悬挂点等效弹簧刚度选择是计算结果的重要影响因素，其中：刚度过小会引起弹簧变形过大，与实际情况不符；刚度过大会导致计算结果误差较大。一般建议标准国际单位下弹簧刚度数值取高于整体波浪载荷数值2个量级。这里选取弹簧刚度为10MN/m、50MN/m和100MN/m进行试算，结果见图3。由于该结构具有对称性，不失一般性，试算时取浪向为0°，故

y

方向的变形为0。本文规定悬挂点变形阈值为0.01m，即在静水与波浪共同作用下，各方向的合成变形不大于0.01m，故取3个方向的弹簧刚度为100MN/m。

图3 悬挂点三向变形量随弹簧刚度变化曲线

22.5°浪向下悬挂点载荷幅频响应因子见图4，其中

F

为力的绝对值。由图4可知，由于平台具有良好的对称性，垂直方向的载荷略大于水平方向的载荷，单位波幅下悬挂点的总拉力接近120kN，对应的波浪频率为0.9rad/s。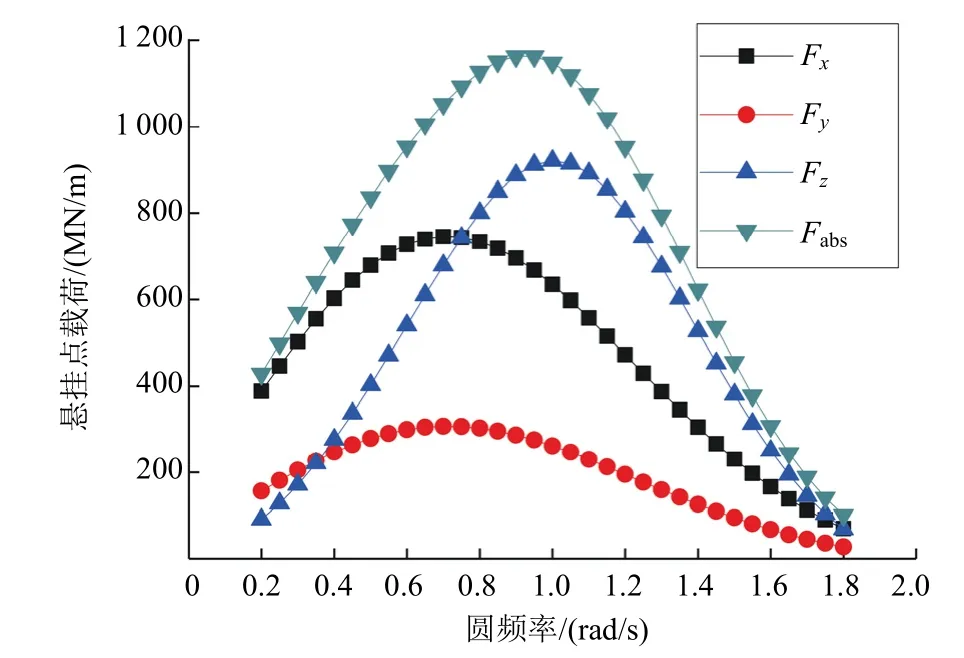

图4 22.5°浪向下悬挂点载荷幅频响应因子

3.2 水动力计算结果

22.5°浪向作用下不同圆频率对应的结构物运动和波浪载荷幅频响应因子见图5和图6。由图5和图6可知：结构物运动响应与波浪载荷RAO均呈单峰形式；运动响应最大值均出现在0.45rad/s频率附近，处于较低频区域；受悬挂点约束作用，结构物垂荡运动为0；波浪力响应最大值出现在0.8rad/s频率附近，垂向波浪力为波浪力的主要成分。

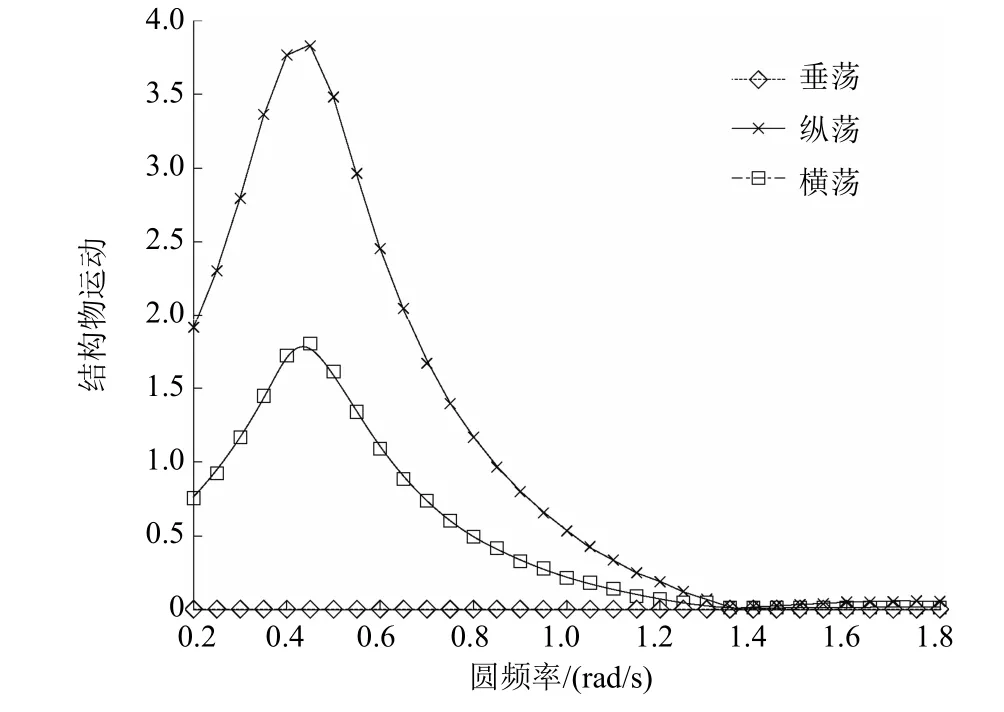
图5 22.5°浪向下垂荡、纵荡和横荡运动曲线

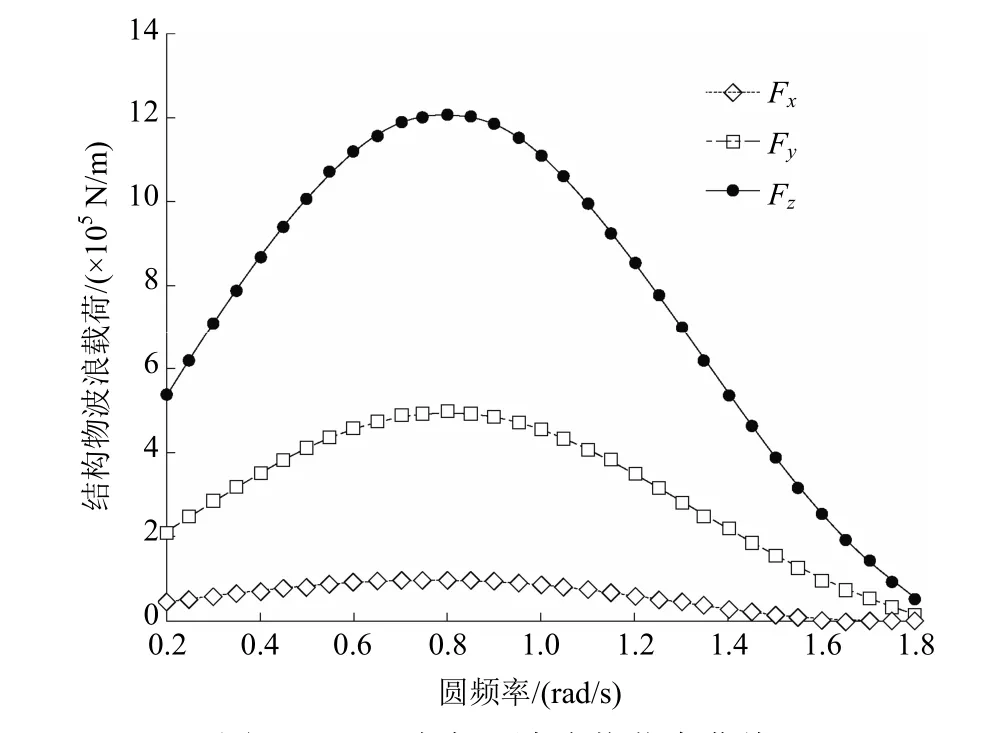
图6 22.5°浪向下波浪载荷力曲线

3.3 强度校核结果

图7～图9为静水+波浪工况下结构应力云图。由图7～图9可知，在静水+波浪组合工况下：最大壳单元Von Mises应力出现在0°浪向、1.05rad/s波频工况下的环形舱上，达到206.7MPa；最大弯曲梁应力出现在22.5°浪向、0.2rad/s波频工况下的底部支撑杆件上，达到306.6MPa；最大拉压梁应力出现在22.5°浪向、1.15rad/s波频工况下的环形舱杆件上，达到40.4MPa。此外，约束点处的应力为1.8MPa，应力较小且无应力集中现象，能表明模型约束的合理性。综上所述，该结构物各部位的结构均满足强度要求。

图7 静水+波浪工况下环形舱壳单元Von Mises应力云图

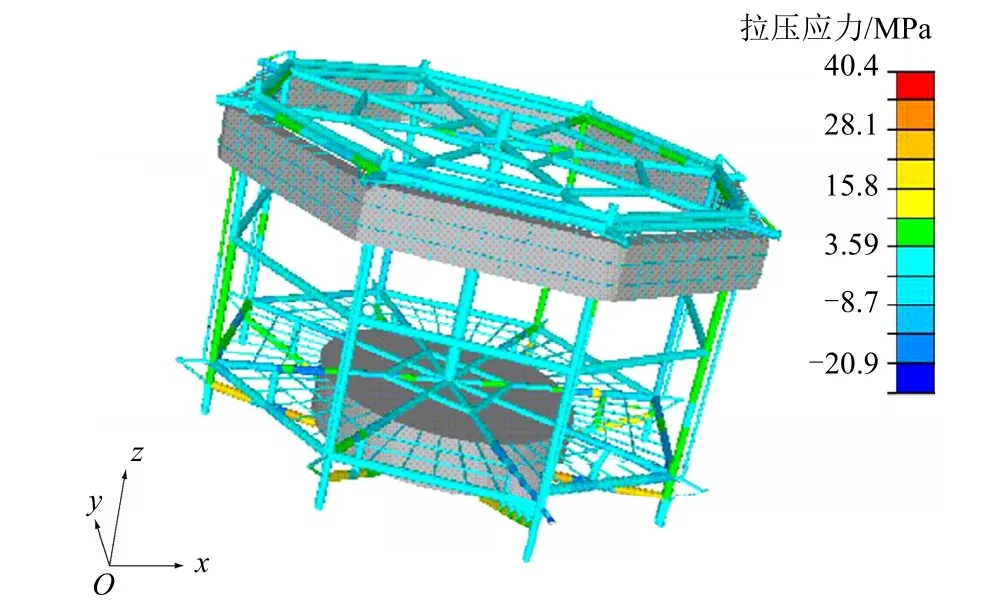
图9 静水+波浪工况下结构物梁单元拉压应力云图

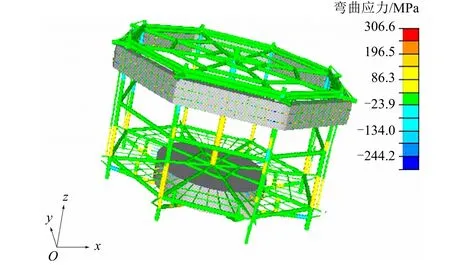
图8 静水+波浪工况下结构物梁单元弯曲应力云图

4 结 语

本文基于势流理论和有限元法研究了单点悬挂式结构物在波浪作用下的动力响应和结构应力，主要得到以下结论：

1) 在研究悬挂点约束作用时，可将悬挂点简化为大刚度线弹簧，在方程中添加附加刚度矩阵，弹簧3个方向的刚度取值建议大于波浪力2个量级。

2) 受悬挂点的约束作用，结构物无垂荡运动，其余波频运动响应最大值均出现在0.45rad/s频率附近。波浪力响应最大值出现在0.8rad/s频率附近。在单位波幅作用下，悬挂点最大载荷为120kN，对应的波浪频率为0.9rad/s。

3) 设计波幅下最大壳单元Von Mises应力出现在环形舱上，达到206.7MPa；最大梁弯曲应力出现在底部支撑杆件上，为306.6MPa；最大拉压梁应力出现在环形舱杆件上，为40.4MPa。由此可知，该结构物的结构强度满足要求。