基于小波分解技术和随机森林算法的负荷概率预测

黄星知，刘 星，张文娟，张永飞

(1. 国网湖南省电力有限公司信息通信分公司，湖南 长沙 410007； 2.北京国电通网络技术有限公司，北京 100070)

现代电力系统中，准确的负荷预测可以在满足技术约束的同时达到卓越的电网运营效果，并提高电力公司和终端用户的财务收益。相关文献研究了在确定性和概率框架下不可调度负荷的内在随机性，其中后者更受关注，因为其可以满足在不确定性条件下进行风险评估和决策的需要[1-6]。文献[1-6]在进行概率负荷预测(Probabilistic Load Forecasting，简称PLF)时讨论了一些非参数方法的特点，包括基于分位数的回归法[2]、集成组合法[3]、分位数回归森林法(Quantile Regression Forests，简称QRFs)[4]和梯度增强回归树法(Gradient Boosting Regression Tree，简称GBRT)[5]等，其中负荷预测追踪[6]进一步提高了预测性能。

与确定性负荷预测相比，这些文献研究突出了PLF特有方法的稀缺性，对比了促进PLF发展的最新趋势。在确定性负荷预测中，通常采用小波分解(Wavelet-Based Decompositions ，简称WBDs)对输入负荷时间序列进行预处理，以通过频谱内容分离各分量，最常见的是与人工神经网络(Artificial Neural Networks，简称ANNs)进行交互使用。

当前，WBDs在PLF中的应用仍在评估中。文献[7]对WBDs在概率可再生能源预测中的一些应用进行了研究，但只有少数文献对PLF中的WBDs进行了研究，而且都是利用ANNs进行预测。文献[8]提出了一种新的集成方法，该方法中母小波和分解层次是不同的，通过偏最小二乘回归将各个结果聚合起来形成集成预测。文献[9]将负荷时间序列通过小波分解成3个分量，并对每个分量应用3个ANNs，为了重建最终的负荷预测，只提出了一种估计预测总体方差的方法。文献[10]将确定性ANNs应用于负荷分量，使用Bootstrapping添加有关预测不确定性的信息。

这些文献研究主要存在以下不足：①使用的是人工神经网络，因此没有其他模型与用于PLF的WBDs相结合；②使用离散小波变换(Discrete Wavelet Transform，简称DWT)来分解负荷时间序列；③通过Bootstrapping或评估点预测的方差来建立概率预测；④概率预测是根据可靠性或清晰度进行评估的，但没有适当的分数用于全面量化概率预测的性能[11-12]。

对于问题④，本文采用一个严格恰当的分数来综合评价负荷概率预测的准确性，并使用特定的图表和指标分别评估概率预测的可靠性和清晰度。本文提出一种新的协同预测系统，以解决问题①～③。该系统采用QRFs进行重要负荷分量的概率预测，用RF进行非重要负荷分量之和的确定性概率预测。每个模型返回预测样本组合以构建最终的负荷预测，避免分位数交叉。

本文使用2014年全球能源预测竞赛(2014 Global Energy Forecasting Competition，简称GEFCOM 2014)[6]公布的实际负荷数据进行仿真分析，并考虑几个概率基准，以便对所提方法的有效性进行全面评估。

1 概率预测系统

本文提出的协同预测系统包括4个步骤，如图1所示。

图1 协同预测系统程序示意图

步骤1：在原始负荷时间序列的WBD中，分离与典型负荷季节性(如每日或每周季节性)相关的特定频率对应的负荷分量。WBD可以捕捉到负荷时间序列的季节性，从而分别处理不同的光谱内容。本文比较了4种不同的WBDs(DWT，WPT，SWT和DT-CWT)，它们以不同的方式分割原始时间序列的光谱内容。具体而言，选择DWT作为基准小波分解，其他3个分解克服了DWT的一些主要缺点，提高了预处理的性能。WPT对沿整个光谱内容的频率进行均匀分解，SWT和DT-CWT则保证了分解对沿时间序列移动的不变性。步骤1的输入是负荷时间序列P，输出是N个负荷分量P(1)，…，P(N)。

步骤2：N个负荷分量被标记为J个重要负荷分量P(s1)，…，P(sJ)和K个非重要负荷分量P(ns1)，…，P(nsK)，其中N=J+K。重要负荷分量满足：①包含负荷时间序列分析中与典型季节性对应的频率；②能量含量高于原始负荷时间序列能量含量的阈值百分比。

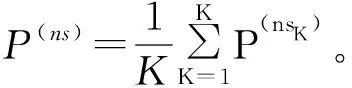
2 基准和误差指数

2.1 基准

本文提出8种概率基准。前3种基准不考虑负荷时间序列的预处理，可以评估用WBD预处理负荷时间序列是否能够提高预测的准确性。第4和第5种基准没有使重要和非重要负荷分量的处理多样化，可用于评估重要和非重要负荷分量的处理多样化是否会提高预测的准确性。第6种基准中用一个确定的模型来计算重要负荷分量之和，用一个概率模型来计算非重要负荷分量之和，因此可评估将概率模型应用于重要分量和确定性模型应用于非重要分量是否优于其他模型。第7种基准主要研究的是与GBRT交互的WBDs，而不是QRFs。第8种基准是一个初步的模型，仅供参考。

(1)QRF基准(版本1)：第一个QRF基准(QRF-B1)改编自文献[13]，直接将单个QRF应用于原始负荷时间序列，以便根据预测分位数构建负荷概率预测。

(2) QRF基准(版本2)：第二个QRF基准(QRF-B2)改编自文献[13]，将单个QRF应用于在[0，1]范围内规范化的负载时间序列，这种标准化可能有助于获得更准确的预测。在这个基准中，所有的外部定量预测因子也都在[0，1]范围内被标准化，对负荷时间序列的平均值(或最大值)的规范化可以返回非常相似的结果，本文中不显示以避免冗长的表示。

(3)GBRT基准：GBRT基准(GBRT-B)基于用于分位数回归的GBRT方法，以适应概率框架，本文是利用R语言中的gbm包开发的。

(4)带WBDs的QRF基准(版本1)：DWT-QRF基准(DWT-QRF-B)、WPT-QRF基准(WPT-QRF-B)、SWT-QRF基准(SWT-QRF-B)和DT-CWT-QRF基准(DT-CWT-QRF-B)将相应的WBD应用于原始负荷时间序列，所有分量都通过不同的QRF进行处理。在实施过程中，不执行步骤2，也不使用确定性预测方法处理任何分量，而是直接按照步骤4进行负荷预测重建。通过试验，DT-CWT-QRF-B在所考虑的所有场景和周期中都优于其他3个QRF基准。因此，本文只将DT-CWT-QRF-B的结果添加到比较分析中。

(5)带WBDs的QRF基准(版本2)：通过将相应的WBD应用于原始负荷时间序列，提出另一种DWT-QRF基准(DWT-QRF-B2)，WPT-QRF基准(WPT-QRF-B2)，SWT-QRF基准(SWT-QRF-B2)和DT-CWT-QRF基准(DT-CWT-QRF-B2)。在这些基准中，通过不同的QRF来处理重要负荷分量和非重要负荷分量之和。实际上，只用到步骤3中的概率预测方法，根据步骤4重构最终负荷预测。通过试验可知，在所有考虑的场景和周期中，WPT-QRF-B2和DT-CWT-QRF-B2优于其他两个基准。因此，本文只将WPT-QRF-B2和DT-CWT-QRF-B2的结果添加到后面的比较分析中，以避免冗余。

(6) 带WBDs的RF/QRF基准：包括基准DWT-RF/QRF-B，WPT-RF/QRF-B，SWT-RF/QRF-B和DT-CWT-RF/QRF-B。在这些基准中，WBD用于负荷时间序列(如步骤1所示)，并且重要负荷分量是个性化的(如步骤2所示)。在步骤3中所采取的操作是相反的：RFs应用于重要负荷分量，QRF应用于非重要负荷分量之和，最后按照步骤4进行最终负荷预测重建。在试验中，DT-CWT-RF/QRF-B在所有考虑的场景和周期方面都优于其他3个基准，因此只将DT-CWT-RF/QRF-B添加到比较分析中。

(7)带WBDs的GBRT基准：带WBDs的基于GBRT的基准(即DWT-GBRT-B，WPT-GBRT-B，SWT-GBRT-B和DT-CWT-GBRT-B)，包括将GBRT用于WBDs产生的重要负荷分量的分位数回归，以及将GBRT用于非重要负荷分量的确定性回归。在试验中，DT-CWT-GBRT-B在所有考虑的场景和周期方面都优于其他3个基于GBRT的基准，因此只将DT-CWT-GBRT-B添加到比较分析中。

(8)初步基准：初步基准(N-B)是基于负荷的持久性的[14]。假设负荷在整个预测提前期内保持恒定，并且每个预测分位数是最后一个观测值(即预测起点处的负荷)，则该基准可以提供一个无偏见、易于复制的参考。

2.2 误差指数

本文主要利用弹球损失(Pinball Loss，简称PL)来比较预测结果。PL是一个严格正确的分数，同时解决了预测的可靠性和清晰度问题。

对于给定的预测范围和分位数水平，PL计算公式为

(1)

总PL是通过Q分位数水平求和并通过预测总数U求平均得到的，PL是一个正的、反向分数，因此较小的PLs表明了更好的概率预测。

采用可靠性评估从概率预测中得到预测区间的一致性，通常通过可靠性图或平均绝对覆盖误差(Average Absolute Coverage Error，简称AACE)指数来进行评估。

本文考虑用可靠性图综合评价方案的可靠性，并用AACE给定负荷预测和标称覆盖率，AACE(百分比)是标称覆盖率和估计覆盖率之间的平均绝对差：

(2)

其中，较小的AAACE值表示更可靠的预测。

采用清晰度评估从概率预测中获得的预测区间的宽度，通常是通过预测区间归一化平均宽度(Prediction Interval Normalized Average Width，简称PINAW)来进行评估。给定U个预测、一个标准值P和标称预测间隔率ρ，该间隔率下的PINAW：

(3)

越小的PPINAW值表示预测越清晰。本文考虑了两个标称预测间隔率(0.1和0.9)下的PPINAWs，并且P是训练期间的最大观测负荷。

3 仿真分析

下面介绍仿真中使用的数据以及使用所提方法得到的预测结果，并与通过基准模型得到的结果进行比较。日前(1～24 h)提供每小时分辨率的负荷预测，此外，在αq=0.01,0.02,…,0.99时，对于每个预测值有Q=99个分位数。所提方法包括DWT-QRF/RF-M,WPT-QRF/RF-M,SWT-QRF/RF-M和DT-CWT-QRF/RF-M，分解层级数为4，以便根据每日季节性分离分量。

3.1 数据特征

本文使用的数据是由GEFCOM 2014的第一个任务1区提供的，预测系统根据2005年1月1日至2010年9月30日的每小时数据进行训练，测试期为2010年10月1日至2011年9月30日(即预测实例)。

在两种不同的场景下分别进行仿真。第一种场景(SC1)下，不使用温度作为RF和QRF的外部预测因子，以便在只有历史负荷可供预测的情况下校验预测性能。第二种场景(SC2)是一个基于温度的场景，使用GEFCOM 2014组织者提供的25个气象站的平均温度作为外部预测因子，以提高预测性能[6]。在这两种情况下，对一天中的一小时、一周中的一天、一个月中的一天和一年中的一个月使用日历进行定性预测，这些日历预测值与文献[14]相同，负荷及温度数据集统计参数见表1。

表1 负荷及温度数据集统计参数

3.2 方法的实施

下面主要讨论QRFs和RFs在MATLAB中的训练和运行，而GBRT是在R语言中训练和运行的。

建立一年每小时预测所需的平均时间(即8 760个预测实例)如表2所示。

表2 平均计算时间

3.3 不考虑温度情况下的场景(SC1)

SC1仿真结果显示，所提方法在较小的预测周期(1 h和6 h)情况下要优于基准模型，在24 h的预测周期下二者差距较小。对于1 h, 6 h和24 h的预测周期，最优方法的PL分别比最佳基准值小13.5%,4.2%和0.2%；在24天的预测期内，WPT-QRF/RF-M的PL最小，比最佳基准(即DT-CWT-QRF-B2)小1.5%。

场景SC1下WPT-QRF/RF-M，WP-QRF-B2和QRF-B2预测方法的损益以及日前水平的提前时间如图2所示。将其与基准WPT-QRF-B2进行比较，以评估不同方法处理重要和非重要负荷分量的影响；与QRF-B2比较以评估WBD对预处理负荷时间序列的影响。由图2可知：当预测周期长达12 h甚至超过19 h时，WPT-QRF/RF-M要优于WPT-QRF-B2；在日前水平上QRF-B2性能不及带WBD的方法。

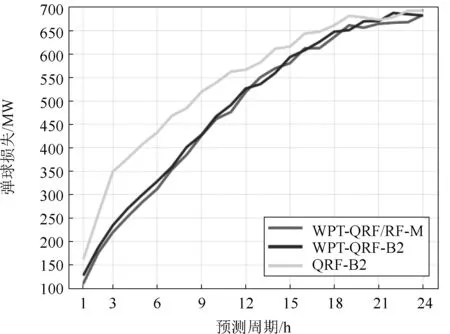
图2 场景SC1中WPT-QRF/RF-M，WPT-QRF-B2和QRF-B2预测方法的损益以及日前水平的提前时间

所提方法可以产生1 h和6 h预测周期的最可靠预测结果，而GBRT-B是24 h预测周期时最可靠的方法。WPT-QRF/RF-M，WPT-QRF-B2和QRF-B2在3个预测周期内的可靠性如图3所示。WPT-QRF/RF-M覆盖率在较高水平上往往被低估，而WPT-QRF-B2和QRF-B2覆盖率总是被高估。DT-CWT-RF/QRF-B在所有考虑的预测周期中是最清晰的方法，但其可靠性较差，从而PL较大。

WBD预处理可提高预测性能，但随着预测周期的增加，这些优势往往会减少。比较最差的方法(即DT-QRF/RF-M)和最好的没有WBD的QRF基准(即QRF-B2)，前者的PL在1 h, 6 h和24 h的周期内分别减小约29.5%，26.5%和1%。将GBRT-B与DT-CWT-GBRT-B进行比较发现，WBD预处理提高了最终负荷预测的性能。这进一步表明，WBDs可以改进概率负荷预测。

分析所提方法的结果和以相同方式处理负荷分量的方法(DT-CWT-QRF-B，WPT-QRF-B2和DT-CWT-QRF-B2)的结果可知，这3个预测周期内的最佳方法都优于最佳基准。但是，最差的方法(即DWT-QRF/RF-M)无法在24 h预测周期内提供小于最佳基准的PL。这表明，对重要和不重要负荷分量进行多样化处理，可以最大限度地缩短预测周期，但性能会随着预测周期的增加而下降。无温度情况(SC1)所获结果如表3所示。

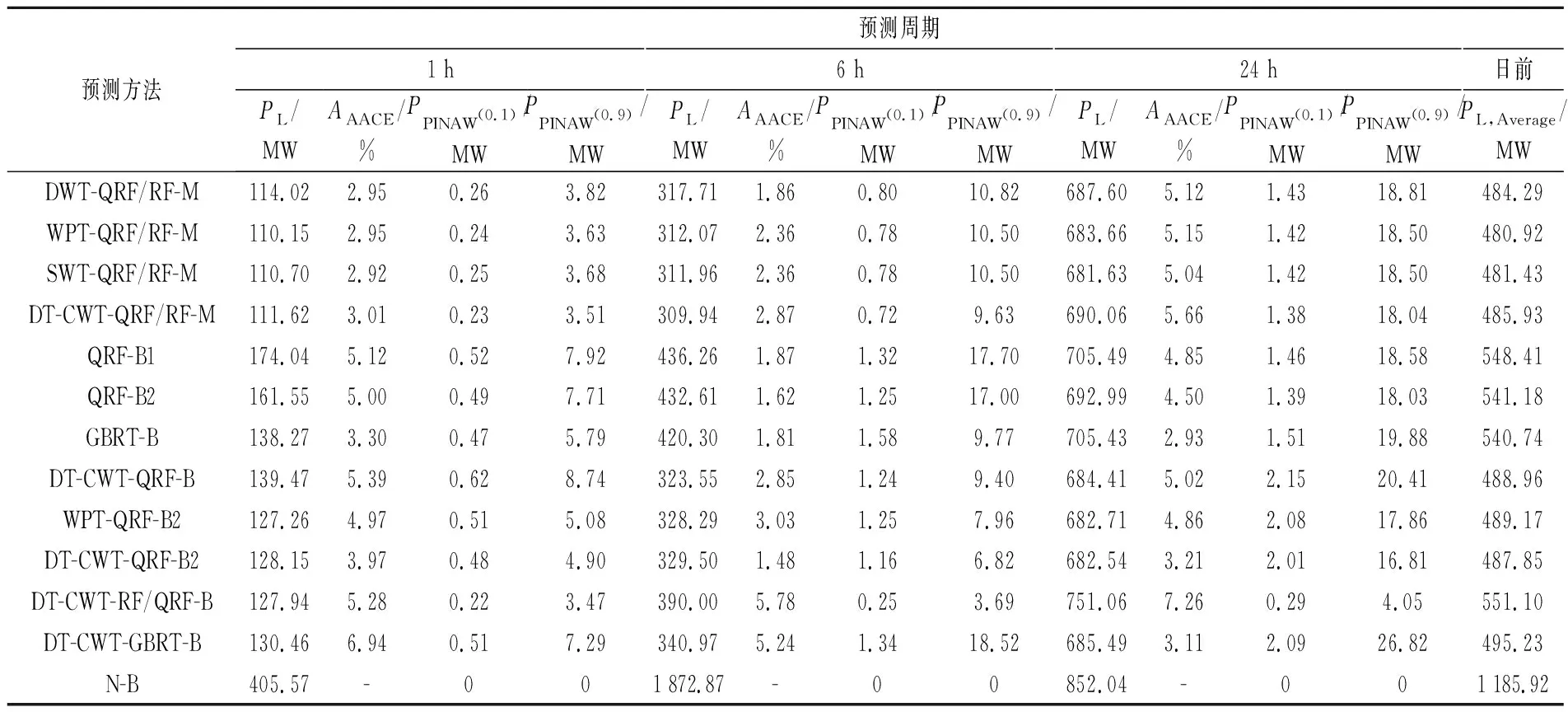
表3 无温度情况(SC1)所获结果

3.4 考虑温度的场景(SC2)

考虑温度的场景下(SC2)的结果如表4所示。所提方法仅在较短的预测周期(1 h和6 h)内优于基准，但在24 h预测周期内，其要优于带WBD的QRF基准。参照最佳基准，最佳方法的PL将减少7.1%(1 h预测周期)，6%(6 h预测周期)，而24 h预测周期的PL则会增加2%。在一天24个预测周期内，SWT-QRF/RF-M的PL最小，比最佳基准(即DT-CWT-QRF-B2)的PL小约1%。

表4 考虑温度的场景下(SC2)的结果

场景SC2下WPT-QRF/RF-M，WPT-QRF-B2和QRF-B2预测方法的损益与日前预测周期的关系如图4所示。由图4可知，WPT-QRF/RF-M仅在10 h内优于WPT-QRF-B2，QRF-B2的准确度低于带WBDs的方法。

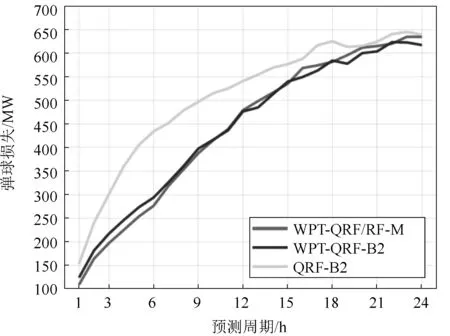
图4 场景SC2中WPT-QRF/RF-M, WPT-QRF-B2和QRF-B2预测方法的损益与日前预测周期的关系

所提方法可以产生最可靠的1 h预测周期的预测结果，而基于GBRT的基准是最可靠的6 h和24 h预测周期下的预测方法。

所用方法中最差的(即DWT-QRF/RF-M)在1 h， 6 h和24 h的预测周期内，PL分别以25%，14.4%和1.2%的比例优于没有WBD的最佳QRF基准(即QRF-B2)。

即使底层模型是GBRT，应用WBD预处理也会提高其准确性，在基于温度的场景中还会进一步提高性能。与场景SC1相反，最佳方法并不总是优于以相同方式处理负荷分量的基准(即DT-CWT-QRF-B，WPT-QRF-B2和DT-CWT-QRF-B2)。特别是，在24 h预测周期内，这些基准的表现要优于所提方法。对重要和不重要负荷分量进行多样化处理，可最大限度地缩短预测周期，但预测性能会随周期的增加而下降。

4 结语

本文评估了WBDs在PLF中的应用，提出了一种基于WBDs的协同预测系统。该系统将重要负荷分量和非重要负荷分量进行分离，分别通过QRFs和RF进行预测，并将所提方法与采用不同模型处理负荷分量的系统、WBD为预处理负荷时间序列的系统以及其他相关基准进行比较。最后，根据GEFCOM 2014年提供的实际数据，通过数值仿真分析验证了所提方法的有效性。所提方法最大的改进是可在最短的预测周期内获得，其中负荷时间序列的WBD提升了预测性能，在1 h的预测周期内，PL减少了29.5%。在未来一天的预测水平上，WPT-QRF/RF-M和SWT-QRF/RF-M的预测结果略好于其他方法，但PL减少不到2%。下一步将进一步研究WBD与其他概率模型的集成，以及基于WBD的新PLF系统的开发等。