基于Particle模型轴流泵固液两相流数值模拟和磨损特性研究
2021-07-15陈松山沈家伟吴志峰钱忠裕周晓润
徐 杰,陈松山,沈家伟,吴志峰,钱忠裕,周晓润
(扬州大学,江苏 扬州 225127)
中国水资源丰富,河流众多,但大部分河流含沙量较高,其中黄河年均含沙量为37.8 kg/m3[1-2],从多泥沙河流中取水的泵站,泥沙的存在不仅对水泵运行参数有显著影响,而且会导致水泵的磨损,机组效率和可靠性下降,危及机组安全运行并造成频繁检修,造成经济损失。因此研究泥沙颗粒对泵装置的影响具有重要意义。
目前国内外在这方面主要研究对象为离心泵和水轮机,汪家琼等[3]运用CFX的Particle模型对离心泵进行数值模拟,结果表明叶片压力面和吸力面的尾部磨损较为严重。黄先北等[4]采用颗粒轨道模型和Tabakoff磨损模型对单吸离心泵进行研究,得到了不同条件下颗粒运动轨迹和磨损规律。张家荣[5]对灯泡贯流式水轮机进行数值模拟,不同浓度不同粒径下泥沙在水轮机组中的分布规律。李远余[6]对高比速混流式水轮机进行数值模拟,揭示了水轮机的磨损位置主要是蜗壳底部、固定导叶和活动导叶头部、转轮进出水边及叶片下侧三角区。王杰等[7]采用欧拉-拉格朗日多相流模型对离心泵内的水沙两相流进行模拟,结果表明泥沙颗粒主要集中在叶片出口表面附近。李昳等[8]分析了不同固相颗粒度和颗粒直径对泵外特性的影响,结果表明当颗粒直径增大或浓度变大时最高效率点会向小流量区域偏移。
以上研究主要针对离心泵和水轮机,然而中国大多数泵站选用的都是轴流泵机组,因此研究轴流泵的固液两相流具有重要意义。本文针对轴流泵进行研究,采用Particle模型和非均相模型以流体为连续相,泥沙颗粒为离散相对竖井贯流泵装置进行固液两相流数值模拟,探讨轴流泵的固液两相流及其磨损特性。
1 计算模型与方法
1.1 计算模型
根据实际竖井贯流泵站1∶1造型并进行数值模拟,其主要设计参数:设计流量Q=36.8 m3/s,转速n=67 r/min,叶轮直径D=3900 mm,固相的浓度Cv=2%~10%,固相即泥沙颗粒的直径d=0.2 mm~1.0 mm,固相的密度ρ=2650 kg/m3等。计算区域见图1,包括进水池、进水流道、叶轮、导叶、出水流道,出水池。
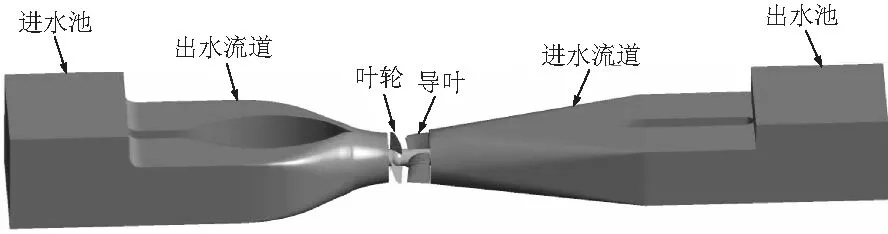
图1 固液两相流竖井贯流泵装置模型
1.2 泥沙受力模型
研究竖井贯流泵装置的固液两相流动,即是研究泥沙颗粒与流体之间的相互作用。正是泥沙颗粒在液体中运动时受到的力决定了其运动特征。这些力主要有重力、阻力、虚拟质量力、压力梯度力、Basset力、Saff man力、Magnus力[9]等,由于本文所研究的泥沙浓度和沙粒直径都较低,可以忽略虚拟质量力、Basset力、Saff man力、Magnus力的影响,其所受重力、阻力和压力梯度力表达式如下:
(1)重力:
(1)
式中:ρp为颗粒密度;dp为颗粒粒径。
(2)阻力:
(2)
式中:CD为阻力系数;ρf为流体密度;uf为流体速度的张量分量;up为颗粒速度的张量分量。
(3)压力梯度力:
(3)
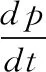
1.3 数值计算方法
文中运用流场分析软件ANSYS-CFX,采用Particle模型对流竖井贯流泵装置内部流场进行固液两相流数值模拟,采用非均相流模型,对于连续流体,采用RNGk-ε湍流模型;对于离散颗粒相,采用离散相零方程模型。由于固相浓度低于20%,相间拖拽力采用Wen-Yu模型[10],忽略非曳力因素影响。求解采用高精度差分格式和方根RMS残差格式,求解精度设为10-4。
1.4 边界条件设定
对于边界条件,计算域的进口采用体积质量流量,然后通过水与泥沙颗粒的体积分数控制它们在流体混合物中所占的比例,计算不同泥沙颗粒体积分数下的流场状态;出口边界条件类型为开放式边界条件;对于水设置为无滑移壁面边界,泥沙颗粒设置为自由滑移壁面边界。
2 计算结果与分析
2.1 模型验证
采用RNGk-ε湍流模型分别对清水工况和泥沙颗粒粒径d=0.2 mm、浓度Cv=2%的含沙水进行数值模拟,并与真机清水实验对比其结果见图2。

图2 实验值与模拟值对比
在清水介质下,模拟值与实验值最大扬程误差为0.1 m,最大效率误差为3.45%,且都出现在较大流量下,在设计流量附近扬程误差为0.01 m,效率误差为2.52%。可以发现外特性模拟值与试验值具有良好的一致性,验证了模型的准确性。从总体上看轴流泵在含沙水介质下,其扬程和效率均略有下降。
2.2 叶片磨损分析
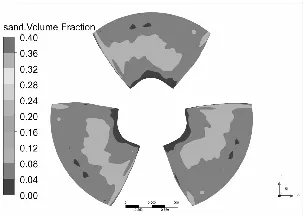
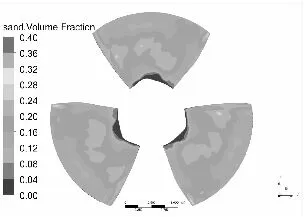
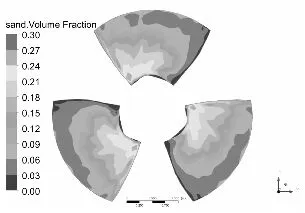
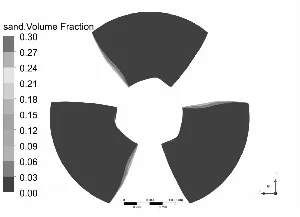
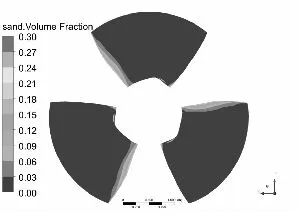
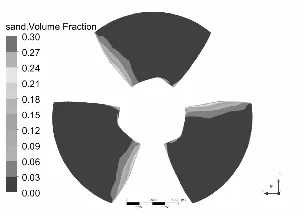
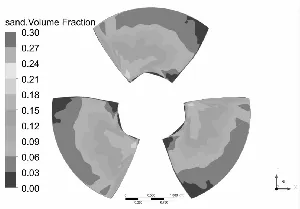
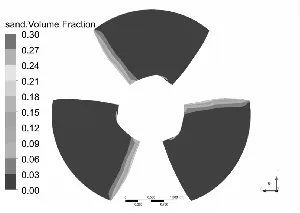
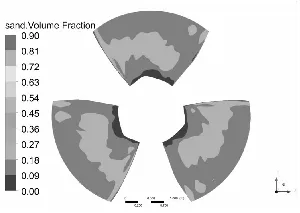
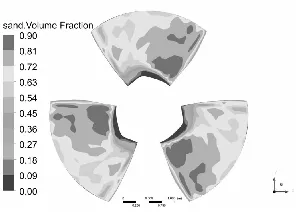
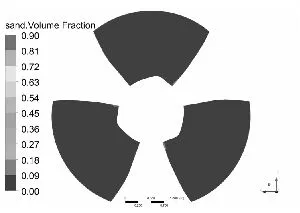
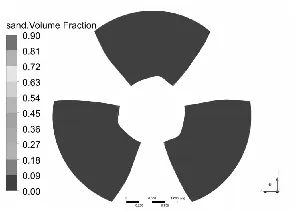
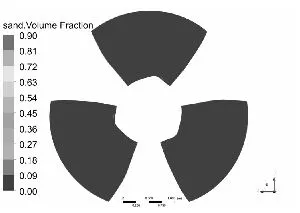
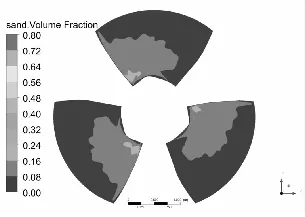
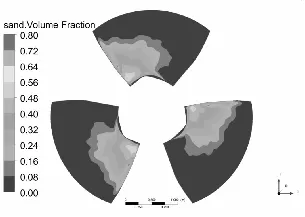
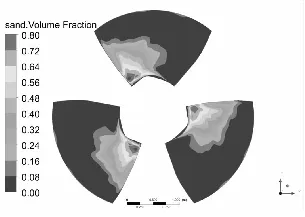
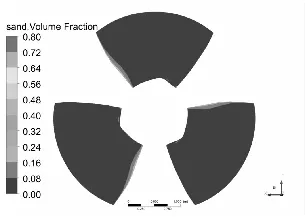
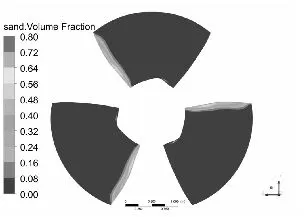
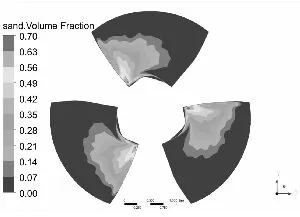
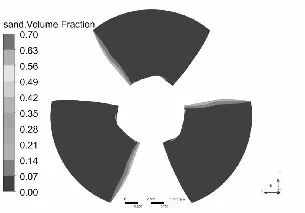
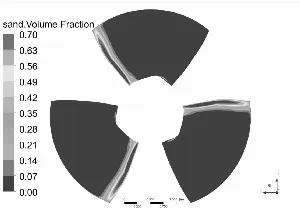
水泵叶片是最重要也是最容易被严重磨损的部件[11-12],图3和图4分别为泥沙颗粒粒径d=0.2 mm下,不同浓度和泥沙浓度Cv=6%下,不同粒径的不同工况叶片表面泥沙分布情况。
Cv=2%
Cv=6%
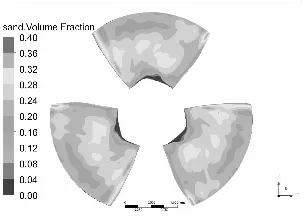
Cv=10%

Cv=2%
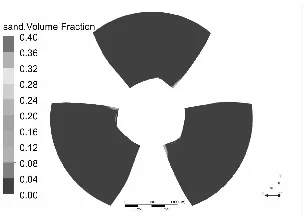
Cv=6%
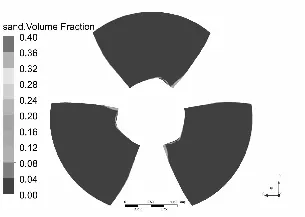
Cv=10%

Cv=2%
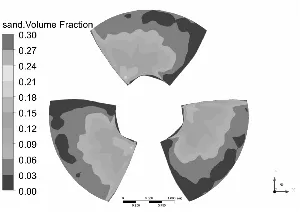
Cv=6%
Cv=10%
Cv=2%
Cv=6%
Cv=10%

Cv=2%
Cv=6%

Cv=10%

Cv=2%
Cv=6%

Cv=10%
d=0.2 mm

d=0.6 mm
d=1.0 mm
d=0.6 mm
d=0.6 mm
d=1.0 mm
d=0.6 mm
d=0.6 mm
d=1.0 mm
d=0.2 mm
d=0.6 mm

d=1.0 mm

d=0.2 mm

d=0.6 mm
d=1.0 mm
d=0.2 mm

d=0.6 mm
d=1.0 mm
从总体上看叶片工作面泥沙浓度高于背面,小流量下叶片工作面泥沙浓度高于大流量工况,这可能是由于小流量下流速较低,产生的离心力不强,泥沙颗粒不易被甩出叶轮域所造成的,另一方面流速较低,泥沙颗粒所具有的动能较小,不易嵌入叶片表面所以小流量下叶片背面几乎没有泥沙分布。从图中可以发现在相同粒径下,叶片表面泥沙浓度随浓度增高而增高,而且叶片工作面高泥沙区域有所增加,但总的分布规律不变。叶片背面浓度也有所提高,且分布区域随浓度升高明显增大。
同样在相同浓度下叶片表面泥沙浓度随沙粒粒径增高而增高,这是由于沙粒粒径增高其所受到重力和阻力都会增大,沙粒也越容易沉积。除小流量外叶片工作面上的泥沙随沙粒粒径增高而越往叶片出口边根部聚集,小流量下则相反。
泥沙颗粒对叶片的磨损分为摩擦磨损和碰撞磨损两种形式。根据文献[13]实验结果表明叶片上的摩擦磨损远大于碰撞磨损,故可以忽略碰撞磨损,摩擦磨损的表达式如下:
(4)
式中:WSL为摩擦磨损率,μm/h;τk为剪切应力,Pa;usk为固相切向速度,m/s。
对于Ni-Cr白口铸铁各相关系数取值如下:
Asl=4.236×1014;Bsl=180;Csl=490;nsl=-3.861。
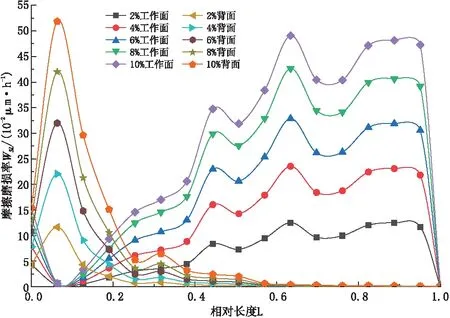
从式(4)中可以看出摩擦磨损与剪切应力、泥沙浓度、泥沙颗粒粒径及切向速度有关[14]。以设计流量Q=36.8 m3/s为研究对象,在一张叶片上从轮毂到轮缘选取3个截面见图7,从而分析整张叶片的磨损情况,并定义3个截面的相对长度为L。

图5 叶片截面截取图

(a)截面1
(b)截面2
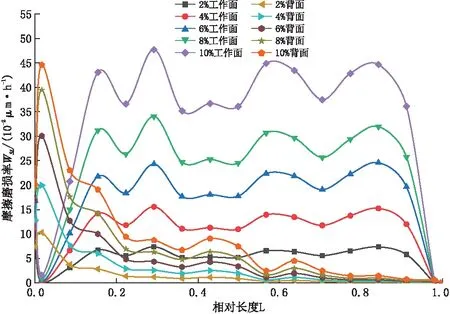
(c)截面3
从图中可以发现叶片各截面的摩擦磨损的分布规律与其泥沙浓度分布规律相似,在叶片相对长度为0~0.2处即叶片进水边,背面磨损率大于工作面;在叶片相对长度为0.6~1.0处即叶片出水边,工作面磨损率大于背面。由于工作面上的泥沙随沙粒粒径增高而越往叶片出水边根部聚集,所以轮缘处(截面3)工作面与背面磨损率差值随粒径增大而增大。在同一粒径下,各截面的磨损率随浓度增大而增大;在同一浓度下,各截面的磨损率随泥沙颗粒的粒径增大而增大,且其增量要高于因浓度改变而造成的增量。
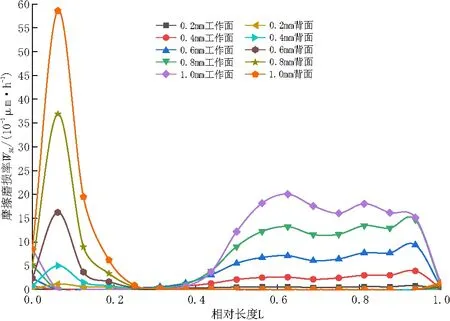
(a)截面1

(b)截面2

(c)截面3
3 结论
(1)泥沙颗粒随着其粒径的增大越往叶片出口边根部分布,而泥沙浓度的变化不会对其分布位置有明显的影响。
(2)叶片的泥沙磨损规律与其表面泥沙浓度分布规律一致,呈现出工作面主要在叶片出水边,背面主要在叶片进水边,它们是叶轮的关键易磨部位。
(3)在高浓度含沙水下条件,叶片工作面磨损率高于背面,所以应注重叶片出水边防磨处理;在高粒径含沙水下条件,叶片工作面磨损率低于背面,所以应注重叶片进水边防磨处理,从而延长叶轮使用寿命。
(4)在低浓度下(Cv≤10%),泥沙粒径是较浓度影响泥沙磨损更为显著的关键因素。
