考虑截齿损耗的多传感信息融合煤岩界面感知识别

2021-07-15王海舰黄梦蝶高兴宇卢士林

煤炭学报 2021年6期

王海舰，黄梦蝶，高兴宇，卢士林，张强

(1.桂林电子科技大学机电工程学院，广西桂林 541004; 2.山东科技大学机械电子工程学院，山东青岛 266590)

如何实现煤岩界面的预先、精准识别是阻碍综采工作面快速、高效开采的瓶颈问题。近年来，随着我国煤炭开采环境、工况趋于复杂，采煤工作面经常出现随机走向的岩石断层，传统的轨迹跟踪记忆截割方法已无法满足煤岩走向突变工况的智能化开采。鉴于目前现有的矿山机械装备及开采技术水平，对煤岩界面的精准识别及智能化、无人化开采的迫切需求日益突出:① 采煤机截割硬岩，势必造成滚筒负载和截割能耗增大、截齿磨损损耗加剧，降低采煤机的截割效率和开采进度，同时，截割硬岩过程中产生的剧烈振动和冲击严重影响采煤机整机的稳定性[1-3];② 采煤机截割岩层会导致原煤中大量夹杂矸石，造成后续煤、矸分选工作量加剧以及原煤热值的降低[4];③ 截齿截割硬岩过程中产生的火花和瞬时高温易引发煤尘或瓦斯爆炸，严重威胁工作人员的生命安全和财产安全[5-6]。

煤岩界面的有效感知识别能够为采煤机提供精准的截割轨迹，实现采煤机避开岩石截割的同时，最大程度的保证煤炭的高效、高质和高量开采。近年来众多专家学者围绕煤岩界面的感知识别问题，展开了大量深入的研究。根据采煤机截割煤岩过程中截割特征信号的变化，部分专家学者提出了基于采煤机截割信号表征的煤岩识别模型，如截割力识别模型、振动频谱识别模型、截割红外识别模型、截割声发射识别模型以及截割电流识别模型。田立勇等[7]通过分析采煤机截割不同煤岩介质时惰轮轴的受力，建立采煤机截割路线的智能预测系统，实现采煤机截割轨迹的实时修正;ZHANG等[8]采用加速度传感器测试放顶煤时的振动信号，将振动信号转换成固有模态函数实现特征提取作为输入，训练整个深层网络的权值并搜索全局最优解，识别精度较高;张强等[9]分析得到采煤机截齿截割煤岩过程中在齿尖一侧均产生突兀的点状闪温区，且截岩时高温区范围与闪温瞬态峰值明显大于截煤过程;杨文萃等[10]推导出声波在水、煤、岩3种介质传输时，在水煤、煤岩2个界面传播、反射的回波公式，构成路径传输煤岩识别声学模型;姜庆学等[11]通过提取和分析采煤机截割煤岩过程中截割电机的有功功率信号，根据有功功率的微小变化进行煤岩的快速识别。

采煤机截割煤、岩过程中的各特征信号虽然在一定程度上能够反映当前的截割介质，但井下实际工况复杂，各种开采机械、运输机械运行噪声严重，开采、运输过程中自身均伴有明显的振动，采煤机截割过程中截齿截割负载、滚筒负载转矩受截割工况、煤岩层自身断裂、破碎等情况影响严重。因此，利用单一截割特征信号实现煤岩界面的识别精度较差，可信度不高，严重时甚至出现失真现象。

随着技术的不断发展，多传感信息融合技术广泛应用到矿山开采与煤岩界面感知识别中。LEI等[12]采用并行拟牛顿算法神经网络和Dempster-Shafer证据理论，提出了一种智能多传感器数据融合的识别方法，通过分析6种截割工况的振动加速度和电流信号，采用融合算法实现截割工况的有效识别;WANG等[13]通过测试煤岩截割过程中的振动、电流、声发射和红外信号，基于最小模糊熵原则，建立多传感信息融合煤岩识别模型。基于多传感信息融合的煤岩识别方法虽然克服了单一信号的缺陷和弊端，有效提高煤岩识别结果的可信度及精度，但该类方法对截割特征信号样本种类、数量需求大，模型维度高，识别结果反馈时效性差。

考虑到煤岩物体特性的差异，部分专家及学者提出了一系列基于煤岩物理特性的识别模型，如雷达探测识别模型、超声波识别模型、图像识别模型以及太赫兹时域光谱识别等。王昕等[14]采用探地雷达方法进行煤岩界面探测，建立了煤岩界面的分层介质模型，结合雷达方程分析了雷达波在该模型中的散射规律，提出了煤岩界面雷达回波强度计算方法;李力等[15]采用改进S变换方法对超声波检测煤岩界面的仿真与实验反射回波信号进行处理，利用时间幅值包络曲线方法分离混叠回波，为煤岩界面的识别提供技术支撑;XUE等[16]采用剪切、灰度变换、对比度增强、中值滤波等方法对综放工作面煤岩崩落的原始图像进行处理，抽取煤岩图像的灰度直方图并计算灰度，实现对煤岩特征的有效识别;WANG等[17]提出了一种基于太赫兹时域光谱技术的煤岩界面识别方法，根据煤岩中不同组分对太赫兹波段的不同响应，采用洛伦兹模型拟合太赫兹波段煤岩的介电特性，实现煤岩界面的快速、稳定和准确识别。利用煤岩的纹理特征、灰度特征以及视觉图像等特征虽然可实现对煤岩界面的精准识别，但现有研究普遍采用实验模拟，煤岩图像的获取条件比较理想，而井下实际开采工作面粉尘浓度大、采光效果差且富含降尘水雾，如此复杂、恶劣的实际工况根本无法获取具有清晰表面纹理或灰度特征的煤岩图像;再者，利用探地雷达、超声波等技术进行煤岩界面的感知和识别虽然不受开采环境影响，但远距离探测往往造成识别效果相对较差，识别精度不高。

综上所述，如何实现开采过程中煤岩界面的精准识别，为采煤机提供精准的截割轨迹，仍是目前矿山煤炭开采亟需解决的瓶颈问题。笔者通过分析采煤机截齿处于不同磨损状态下截割煤岩时，其振动信号、电流信号、声发射信号以及红外闪温信号的差异性，建立截齿不同磨损程度下的截割特征信号样本数据库，以最小模糊熵为优化目标，优化求解截齿处于不同磨损程度的多特征信号隶属度函数，从而有效提高煤岩界面的融合识别精度，对实现采煤机自动化高效开采以及无人化智能采煤具有重要的研究意义。

1 多信息融合煤岩界面识别实验台

1.1 煤岩截割特征信号分析

截割介质的变化对截割特征信号的变化会产生显著影响，采煤机在截割煤、岩过程中，截割滚筒与煤、岩产生剧烈碰撞和摩擦，采煤机的滚筒振动、截割电流、截割声发射以及截割红外闪温信号均能不同程度的反应当前的截割介质。

1.1.1截割振动信号

采煤机滚筒截割煤岩过程中，截齿与煤岩产生剧烈碰撞和摩擦，导致滚筒及摇臂发生明显的振动，利用三向振动传感器检测采煤机截割不同比例煤岩界面时的振动信号(图1)，发现滚筒在进给方向(x)、垂直方向(y)以及轴向(z)3个方向上的振动随煤岩比例的变化发生变化，通过进一步分析发现滚筒垂直方向(y)振动幅度的变化随截割煤岩比例的变化具有显著的规律性，因此，采用采煤机滚筒截割煤岩过程中y轴的振动信号作为多信息融合识别系统的特征信号。

1.1.2截割电流信号

采煤机滚筒的动力传动系统如图2所示，主要由截割三相异步电动机、滚筒机构以及多个传动齿轮构成。由于煤岩介质的物理特性不同，采煤机滚筒在截割不同比例煤岩过程中，受到的截割阻力差异很大，而滚筒负载的变化将直接影响采煤机截割电机电流的大小，因此，可以通过采煤机截割电机电流的变化实现采煤机滚筒截割过程中煤岩截割比例的分析和识别。

1.1.3截割声发射信号

采煤机在截割煤岩过程中，煤、岩受截齿的挤压和冲击而导致受力变形，在煤岩自身体内原有或新产生的裂纹处形成应力集中并快速扩展，其内部贮存的能量以弹性应力波的形式释放并向外传播，因此，根据声发射信号的强弱、幅度的大小可以分析采煤机截割过程中的煤岩比例情况。但煤、岩介质均属于非弹性体，声发射信号在其传播过程中会发生波动能量损失，因此，当声发射传感器位置固定不变时，采煤机滚筒处于不同位置截割煤岩时，其声发射信号振幅的衰减程度会随着距离的增大而增大，需要考虑采煤机与测试传感器之间的距离对声发射信号强度的影响。

采煤机在截割煤岩过程中，其位置和姿态均会发生改变，如图3所示。

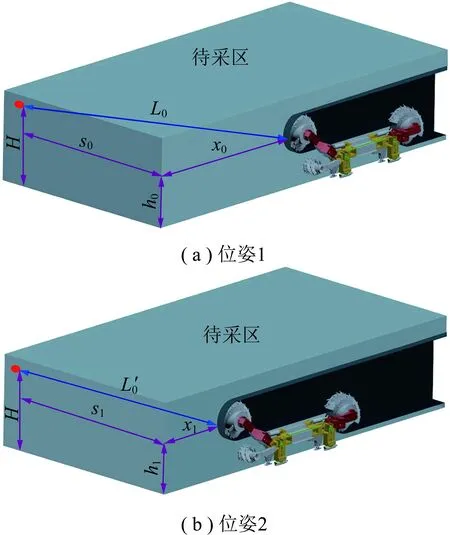
图3 采煤机不同位姿状态下声发射信号检测Fig.3 AE signal detection of a shearer in different positions

由图3可知，采煤机在不同位姿截割状态下，其截割声发射信号产生位置与声发射检测传感器的距离分别表示为

(1)

式中，L0，L′0为采煤机处于不同截割位置时声发射源与声发射传感器的直线距离，m;H为声发射传感器的安装高度，m，通常为固定值;h0，h1为采煤机前滚筒中心距地面的高度，m;x0，x1为采煤机处于不同位置时滚筒前端声发射源距声发射传感器安装平面的铅锤距离,m;s0，s1为声发射传感器与采煤机当前开采截面的铅锤距离，m。

综合应力波传播衰减理论、品质因子Q理论，可以得出声发射信号在煤岩体传播过程中的振幅变化函数为

(2)

式中，A(L)为声发射信号自发生位置传播L距离后的振幅，mV;A0为声发射信号产生时的初始振幅,mV;α为声发射的衰减系数;f为声发射信号的频率，Hz;v为声发射信号在介质中的传播速度，m/s;Q为煤岩介质的品质因子。

结合式(1)，(2)可得到单位距离ΔL的振幅衰减程度为

(3)

根据式(3)可以得到采煤机不同位姿状态下截割煤岩过程中的真实声发射信息，作为煤岩界面识别的特征信号。

图4 截齿不同截割工况的红外图像及温度特征Fig.4 Infrared image and temperature characteristics under different cutting conditions of picks

1.1.4截割红外闪温信号

采煤机在开采过程中，截齿与煤、岩产生剧烈碰撞和摩擦，造成截齿齿面温度场的瞬时显著变化，而截齿的瞬时闪温值受采煤机位姿状态影响很小，可忽略不计。利用高速的红外热像仪采集截齿截割不同比例煤岩过程中的瞬时闪温特征，如图4所示，其中，Tmax为闪温峰值。由图4可以看出，截割工况不同时，截齿齿尖瞬时闪温区的温度场差异很大，瞬时闪温峰值也各不相同，通过大量实验室测试结果可知，截割过程中，岩层比例越大，其瞬时闪温峰值越高，利用这一特征，可以实现煤岩界面的感知识别。

1.2 煤岩界面识别实验台搭建

采煤机煤岩截割实验台的搭建要综合考虑采煤机的机械结构，并以截割理论、相似理论、相似系数为基础。本文主要研究根据不同煤岩比例截割过程中多信号的表征差异来实现煤岩界面的有效识别，因此搭建的采煤机煤岩截割实验台主要实现采煤机的行走、截割等相似功能，而无需根据相似理论和相似系数对采煤机煤岩截割实验台对各机构进行设计。根据滚筒式采煤机的主要机械结构特征以及各特征信号的采集需求，建立采煤机煤岩截割实验台的机械系统、数据采集与控制系统以及上位机数据分析系统如图5所示。

图5 采煤机煤岩截割实验台Fig.5 Coal-rock cutting experimental station of a shearer

采煤机煤岩截割实验台的截割电机为380 V三相异步电动机，额定功率为0.55 kW，额定转速为1 500 r/min，蜗轮蜗杆减速器主要用于降低采煤机滚筒的转速，增大滚筒的负载转矩，其减速比为38∶1。滚筒上共安装4支神东天隆公司生产的U85型截齿，滚筒截割直径为320 mm，截割深度为60 mm，滚筒转速为60.53 r/min。实验台的数据采集系统包括声发射信号采集系统、红外热像采集系统以及振动与电流测试系统三大模块，用于测试采煤机滚筒截割不同比例煤岩时的声发射信号、红外闪温信号、振动信号及电流信号。

1.3 煤岩试件的制备

为了便于表达不同比例的煤岩界面，定义采煤机滚筒截割煤的弧长占滚筒与煤岩总接触弧长的比例的比值为“截煤比”。如图6所示，L1和L2分别为采煤机滚筒截割煤、岩的弧线长度，则采煤机滚筒截割煤的弧长占煤岩总接触弧长的比例为L1∶(L1+L2)，即为“截煤比”。

图6 煤岩截割比例Fig.6 Coal-rock cutting proportion

想要实现煤岩界面的精准识别，就要获取不同“截煤比”煤岩试件截割过程中的多信号特征，从全煤到全岩试件，可以把煤岩的比例进行不断的细致划分，煤岩比例划分的越细致，则获得的不同截煤比的多传感特征信息越完善，构建的煤岩识别模型精度越高。但过度的精细分割容易导致数据处理和分析工作量过大，数据训练的难度、信息融合的维度以及模型的计算量大大增加，甚至容易由于数据量过大或维度过高导致识别模型无法正常工作。综合考虑上述2点，笔者共构建7种不同截煤比的煤岩试件，其截煤比分别为0∶1(全岩),1∶5,1∶3,1∶2,2∶3,4∶5和1∶1(全煤)，每种截煤比的煤岩试件浇筑5块，浇筑成型后待截割实验的7种截煤比煤岩试件如图7所示。

图7 不同截煤比煤岩试件Fig.7 Coal-rock specimens with different coal cutting proportions

为了准确分析煤岩试件的性质，需要对浇筑煤岩试件的煤、岩物理力学性质进行测定。考虑到性质测定实验对试件的尺寸要求，采用标准试件模具分别浇筑实验所需数量的煤、岩标准试件，标准试件为直径50 mm、高度100 mm的圆柱体，煤、岩试件各制备12个。煤样中，煤、水泥、粘合剂的配比为4.0∶1 .0∶0.1，岩样中，沙子、水泥、粘合剂的配比为3.5∶1.0∶0.2。采用单轴实验对煤、岩标准试件的单轴抗压强度、弹性模量、泊松比、高径比以及密度进行测定，如图8所示。最终得到模拟煤、岩层的材料性质测定结果分别见表1。

图8 煤岩试件性质测定实验Fig.8 Property determination experiment of coal and rock specimens

表1 模拟煤、岩层材料性质测定结果Table 1 Determination results of material properties for simulated coal or rock seam

2 考虑截齿损耗的隶属度函数优化

2.1 截齿损耗对截割特征信号影响分析

采煤机截割煤岩过程中，滚筒上各截齿与煤、岩发生连续碰撞和摩擦，随着开采时长的增加，截齿的磨损程度也不断加剧，根据截齿截割过程中的磨损特征，可将其分为新齿、轻微磨损、一般磨损、严重磨损和磨损失效5个阶段，如图9所示。而由于磨损失效状态下的截齿已完全不适用于采煤机截割，因此，本文主要研究新齿、轻微磨损、一般磨损和严重磨损4个磨损状态下截齿的截割信号特征。新齿，即安装后未进行煤岩截割的截齿;轻微磨损的截齿受煤岩的碰撞冲击，其齿尖由尖锐状过渡到略微圆滑状态;一般磨损的截齿较轻微磨损截齿其齿尖的凸起度明显下降，但仍然保持较好的截割性能;而严重磨损的截齿其齿尖已近乎磨损殆尽，截齿截割性能明显下降，各磨损状态截齿如图10所示。

图9 不同磨损程度截齿对应的磨损量及截割效率Fig.9 Wear loss and cutting efficiency of picks with different wear degree

图10 不同磨损程度截齿Fig.10 Peaks with different wear degree

随着截齿磨损程度的加剧，采煤机滚筒的截割效率加速退化，与此同时，截齿磨损程度的变化会对截割过程中的各特征信号产生显著的影响。通过构建的煤岩截割实验台开展实验测试，采用新齿、轻微磨损、一般磨损、严重磨损4种磨损程度的截齿分别截割截煤比为1∶2的煤岩试件得到截割过程中的振动信号、电流信号、声发射信号及红外信号特征样本值分别见表2。

表2 不同磨损程度截齿截割过程中多特征信号数据Table 2 Multi characteristic signal data in cutting process with different wear degree of picks

由表2不同磨损程度截齿截割过程中各特征信号的数据可以看出，新齿状态与严重磨损状态下的振动加速度方根幅值和电流有效值分别相差0.040 4g(g为重力加速度)和85 mA，新齿状态与严重磨损状态下的声发射小波重构能量与红外闪温值分别相差5.58和1.40 ℃，通过开展30次重复试验，发现随着截齿磨损程度的加剧，振动加速度方根幅值及电流有效值明显增大，而声发射小波重构能量和红外闪温值随着截齿磨损程度的加剧不断降低。因此，如果仅根据某一种截齿磨损状态下的多截割特征信号样本构建煤岩界面的融合识别模型，不具备普适性，煤岩界面识别结果容易造成很大的误差，导致识别精度不高。

2.2 不同磨损程度截齿截割特征信号分析

为了分析不同磨损程度截齿截割煤岩过程中各特征信号的变化规律，利用构建的煤岩截割实验台，分别采用新齿、轻微磨损、一般磨损、严重磨损4种磨损程度的截齿截割7种不同截煤比的煤岩试件，测试、采集截割过程中的振动信号、电流信号、声发射信号及红外闪温信号如图11所示。

图11 不同磨损程度截齿截割7种截煤比煤岩试件特征信号Fig.11 Characteristic signals of peaks with different wear degree while cutting coal-rock specimens with seven coal cutting proportions

由图11可以看出，截齿在截割不同截煤比煤岩试件时，其振动信号、电流信号、声发射信号及红外闪温信号均随着截煤比的减小而显著增大，且各个截割信号相邻2个截煤比的特征值存在一定交集，即2者并不是相互独立的，具有一定程度的模糊性。此外，对比同一信号在不同磨损程度截齿截割过程中的特征值可以看出，随着截齿磨损程度的变化，各截割信号的特征值发生显著的变化，其中，振动加速度方根幅值和电流有效值随着截齿磨损程度的加剧而显著增大，这是由于在进给速度、滚筒转速以及截割深度恒定的工况下，由于截齿磨损的加剧，截齿截割、破碎煤岩的能力下降，截割过程中阻力明显增大，产生的振动与冲击显著增强;而声发射小波重构能量和红外闪温值随着截齿磨损程度的加剧不断降低，这是由于随着截齿磨损的加剧，截齿表面逐渐钝化，截齿与煤岩接触的表面受力逐渐趋于均匀，截齿截割过程中的瞬时闪温区逐渐增大，闪温峰值逐渐减小。因此，想要实现不同截齿磨损状态下煤岩界面的精准识别，需要充分考虑截齿磨损对多截割特征信号的影响，需根据截齿实际的磨损程度，实时分析各截割特征信号反映的真实煤岩比例特征。

2.3 基于最小模糊熵的隶属度函数优化

定义煤岩界面识别系统的样本模糊集为X={x1,x2,…,xn}，其对应的隶属度函数为μj(x)，当μj(x)取值为0或1时，其对应的第j个集合Aj为分明集，模糊熵值为0;当隶属度μj(x)⊂(0,1)时，其模糊熵的表达式为

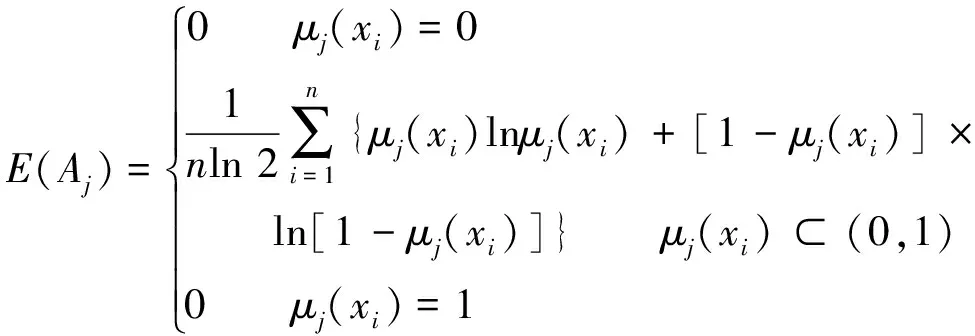
(4)

式中，n为模糊系统中所有特征样本的总数;xi为模糊集X中的第i个特征样本;μj(xi)为第i个特征样本对第j个子集Aj的隶属程度。

煤岩识别系统不同截割比例状态的模糊集为{全煤,截煤比4∶5,截煤比2∶3,截煤比1∶2,截煤比1∶3,截煤比1∶5,全岩}，分别用集合{A1,A2,A3,A4,A5,A6,A7}表示。对应的各模糊子集的隶属度函数为μ1，μ2，μ3，μ4，μ5，μ6和μ7。

针对隶属度函数的最优确定还没有一套成熟有效的方法，绝大多数隶属度函数的确定方法主要依托经验和实验，常见的隶属度函数有三角形、梯(半梯)形、高斯型以及S型等。其中三角形是最简单的隶属函数，它是用直线形成的，梯形隶属函数实际上是由三角形截顶所得。这2种直线形隶属函数都具有简单的优势，在基于模糊推理的信息融合方法中得到广泛使用，因此，本文采用两端为梯形，其余为三角形的隶属度函数构造方法建立系统的隶属度函数模型，其隶属度函数图如图12所示，图中k1～k7为对应的μj(x)隶属度函数的阈值。

图12 煤岩截割比例隶属度函数Fig.12 Membership function of coal-rock cutting proportion

由于系统的模糊度越大，其模糊熵值越大，因此实现模糊系统中模糊熵的最小化能够实现系统模糊隶属度值的最大化。由图12可知，实现隶属度函数优化求解的本质就是实现对隶属度函数各阈值ki的优化求解。结合式(4)，根据最小模糊熵原则构建模糊系统的隶属度函数优化模型[18-19]:

[1-μj(xi)]ln[1-μj(xi)]}

(5)

根据图12定义的隶属度函数，当下标j为最小值1或最大值7时，其隶属度曲线为梯形，μ(x)的表达式为

当下标j=2，3，4，5，6时，隶属度函数为三角形，μ(x)的表达式为

PSO算法是1种基于迭代模式的求解优化算法，每个粒子代表极值优化的1个潜在最优解，其粒子特征采用位置、速度和适应度值3个指标来表示[20]。假设共有N个粒子，其位置信息均为d维，则每个粒子的当前位置xi、历史最优位置pi、速度vi可分别表示为

xi=(xi1,xi2,…,xid)

(6)

pi=(pi1,pi2,…,pid)

(7)

vi=(vi1,vi2,…,vid)

(8)

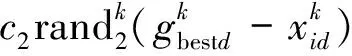
(9)

(10)

式(9)中，PSO算法容易陷入局部最优值，粒子易于趋向同一化，不能直接应用于求解多目标优化问题，因此，本文引入惯性权重系数[21-22]来克服这一问题，即

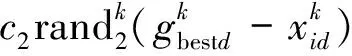
(11)

其中，w为非负数，称为惯性权重系数或惯性因子，用来平衡算法的全局搜索能力和局部搜索能力，w较大时，全局搜索能力较强;w较小时，局部搜索能力就强。为了实现搜索速度和搜索精度的平衡，通常在优化前期获得较高的局部搜索能力以获取合适的种子，而在后期为提高收敛精度需要保证系统具有较高的局部搜索能力。因此，惯性权重系数w的取值不宜为固定常数，本文采用线性递减惯性权重方法获取算法的惯性权重系数w:

(12)

式中，wmax为最大惯性权重;wmin为最小惯性权重;t为当前的迭代次数;Tmax为算法的迭代总次数。

PSO-最小模糊熵多传感特征隶属函数优化求解过程是以不同截煤比煤岩试件截割过程中的多信号特征样本为基础，以最小模糊熵为优化准则，结合粒子群优化算法对隶属度函数多目标阈值进行优化求解，最终得到模糊度最小的隶属度函数。各截割特征信号模糊熵值的迭代优化曲线分别如图13(a)～(d)所示,可以看出，不同磨损程度截齿的各截割特征信号样本迭代优化过程中，在80次迭代步数内均达到收敛，收敛速度较快。根据优化后得到的隶属度函数阈值求解结果构建截齿不同磨损程度时多特征信号的隶属度函数图，如图13(e)～(h)所示,可以看出，各截割特征信号的隶属度函数图随着截齿磨损状态的改变发生显著变化，截齿轻微磨损、一般磨损以及严重磨损状态下的阈值优化结果较新齿发生明显的偏移，表明截齿在不同磨损状态下，分别独立对应适宜获取高精度识别结果的隶属度函数，采用单一新齿状态下的隶属度函数无法保证截齿处于不同磨损状态下截割时，对煤岩界面的准确感知识别。图13(e)～(h)得到的隶属度函数优化结果为之后准确计算截齿不同磨损状态下截割特征信号的隶属度，实现多特征信号D-S融合决策奠定基础。

3 基于D-S的煤岩界面融合识别

3.1 基本概率分配函数

定义m1,m2,m3和m4分别为振动信号、电流信号、声发射信号和红外闪温信号的基本概率分配函数，结合图13优化求解得到的各特征信号不同截齿磨损程度的隶属度函数，构造各证据体赋予其各模糊子集的基本概率赋值mi(Aj)以及证据体的不确定性描述mi(Θ)的求解公式分别为

(13)

(14)

其中，μi(Aj)为证据体Ei对截煤比识别框架中命题Aj的隶属程度;δi为第i个证据体对具有最大隶属度及次大隶属度的两个命题的差值，该值从最大隶属度的突出程度角度反映系统识别的可靠性;γi为除最大值命题外，第i个证据体对其余命题隶属度的方差，反应决策结论的可靠性;φi为第i个证据体的权值，用来提高煤岩界面识别的正确性。由于融合模型中证据体包含多个截割特征信息，不同信号识别过程中的灵敏度和可靠性存在很大差异，因此，不同的证据体权值分配对融合决策识别结果的精确程度具有重要影响。δi与γi的数学表达式分别为

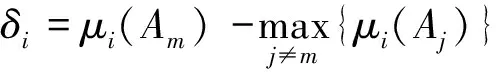
(15)

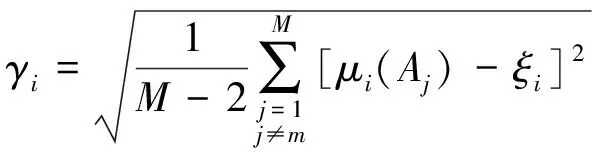
(16)

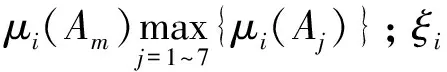
图13 最小模糊熵迭代优化曲线及优化后隶属度函数Fig.13 Iterative optimization curves based on minimum fuzzy entropy and optimized membership functions

3.2 D-S证据理论信息融合规则

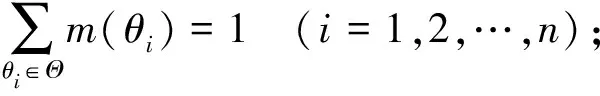
则称m(θi)为事件θi定义在2Θ上的基本概率分配函数，m(θi)为证据支持命题θi发生的程度，而不支持任何θi的真子集。当m(θi)>0时，则称θi为证据的焦元。所有焦元的集合称为核[24]。

(17)

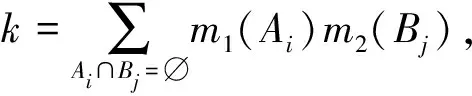
通过式(17)可以看出，D-S证据理论信息融合技术就是将2个或2个以上单一信任函数的概率分配函数，通过计算得到新的基本概率分配作为最后的决策依据。由此可以推导出多信任函数的证据组合规则为

m={[(m1⊕m2)⊕m3]⊕…}⊕mn

(18)

式中，m1,m2,…,mn分别为同一识别框架2Θ上信任函数Bel1,Bel2,…,Beln的基本概率分配函数;⊕为正交求和。

3.3 D-S证据理论融合决策准则

为了实现对采煤机截割过程中煤岩界面的精确识别，避免采用单一信号进行识别时信度比较低等缺陷和不足，采用多规则“与”判定的决策方法对煤岩界面进行识别，其各识别决策准则为

准则2:Bel(Am)-Bel(Aj)>ε，Bel(Am)-mi(θ)>ε(ε>0且ε∈R);

准则3:mi(θ)<λ(λ>0且λ∈R)。

准则1用来表明识别命题结果具有最大的信度;准则2说明识别结果的信度与其他任意命题的信度差值要大于阈值ε;准则3证据的不确定性必须小于限值λ，ε与λ的取值需根据实际情况来确定。多规则“与”判定决策方法要求识别结果必须同时满足上述3个准则，缺一不可，如若以上3个规则不能同时满足，则判定与决策终止，无法确定煤岩界面识别结论。

3.4 基于识别结果可信度的截煤比识别优化

由于本文隶属度函数是根据定义的7种截煤比构建，因此，识别结果只能是7种截煤比之中的一种，但实际煤岩截割比例经常存在处于2种截煤比之间的情况，因此，想要得到准确的煤岩界面识别结果，还要根据识别结果的信度值对不同截煤比进行优化，从而得到更为精确的识别结果。

通过大量实验结果分析可知，识别结果对不同截煤比的信度值在一定程度上反映了实际煤岩比例对定义的截煤比的趋近程度。图14反映了部分识别采样点具有最大信度、次大信度以及第三大信度的截煤比识别结果，可以看出，实际煤岩轨迹在各采样点均分布在具有最大信度和次大信度的截煤比识别结果之间，且相对接近于具有最大信度的截煤比识别结果，对于次大信度截煤比识别结果具有一定程度的趋向性，且最大信度和次大信度的差值越大，识别结果对具有次大信度值的截煤比的趋向性越小，真实的截煤比越逼近具有最大信度值的截煤比识别结果。反之，识别结果对具有次大信度值的截煤比趋向性越大。因此，识别结果信度值的大小很大程度地反映了与真实煤岩比例的逼近程度。

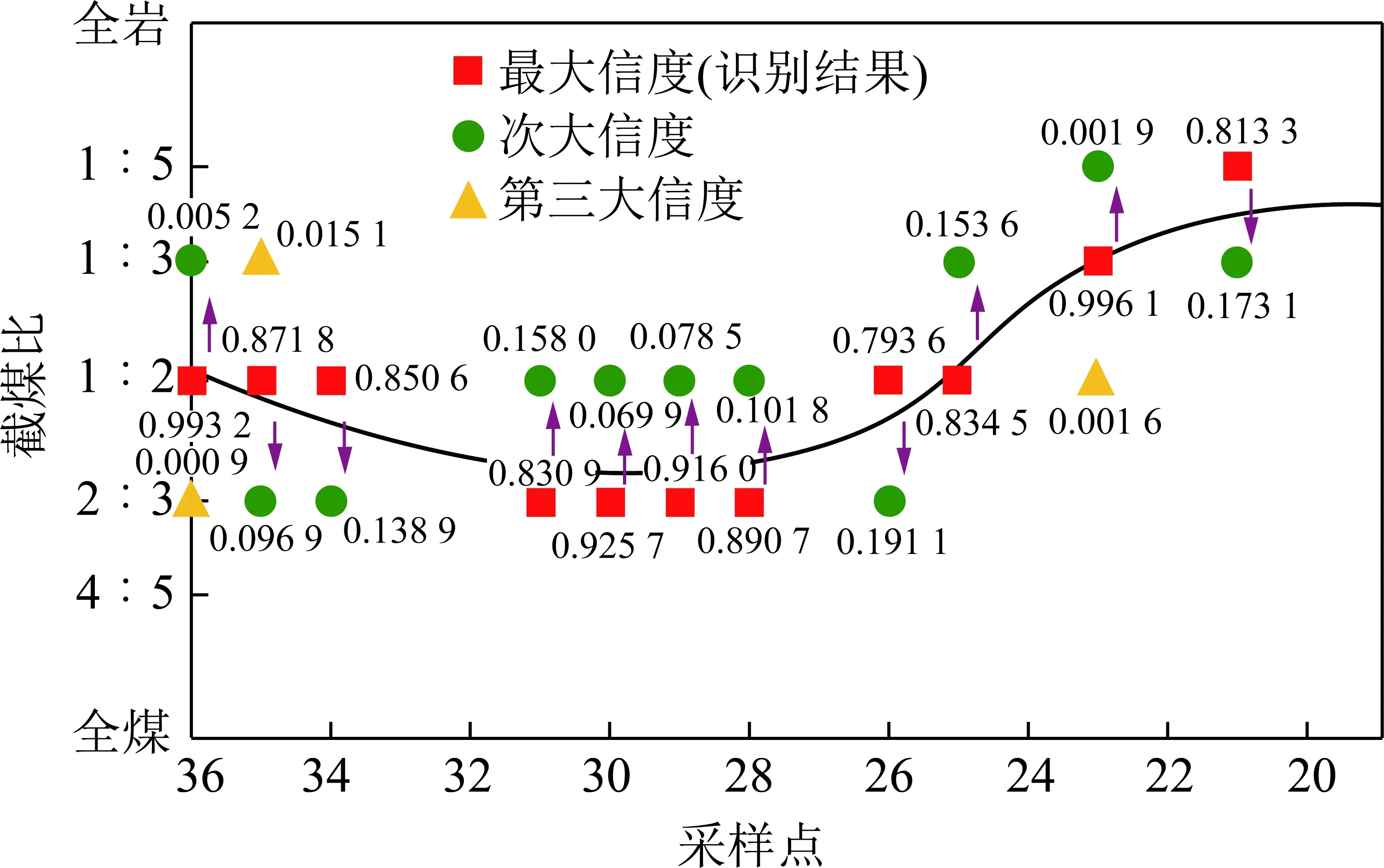
图14 截煤比识别结果信度分布及趋向性分析Fig.14 Reliability distribution and trend analysis of coal cutting proportion’s identification result

若定义第i组样本融合结果中拥有最大信度目标的信度值为mi(Aj)，拥有次大信度目标的信度值为mi(Ak)，Aj，Ak为2个相邻识别目标的截煤比值，用Li表示当前样本采样点的截煤比修正值，则有

(19)

通过式(19)，可以将煤岩界面识别结果由固定的7种截煤比进一步精确化，使其更加逼近真实的煤岩轨迹。

4 实验验证与精度分析

4.1 实验分析

考虑到实际煤岩界面的不确定性和随机性，实验室浇筑4块具有相同随机煤岩走向分布界面的截割试件，试件中煤、岩的成分、配比与本文浇筑的标准试件一致。分别采用新齿、轻微磨损、一般磨损和严重磨损4种状态下的截齿截割浇筑的随机走向煤岩试件，如图15所示。截割过程中分别测试振动信号、电流信号、声发射信号以及红外闪温信号，每个试件截割过程中采集30组特征样本，利用图13优化后的截齿不同磨损程度的隶属度函数，计算各个样本对不同截煤比的隶属程度，基于构建的D-S证据理论融合规则，对不同磨损程度的多特征信号进行融合，并根据式(19)对各采样点的识别结果进行优化修正，得到不同磨损程度截齿截割时的识别结果分别如图16所示。

图15 随机煤岩试件截割实验Fig.15 Cutting experiment of random coal-rock specimen

图16 不同截齿磨损状态下截割特征信号Fig.16 Feature signals under different peak wear degrees

采用定量分析方法分析不同磨损程度截齿截割时的识别结果精度，如图17所示，煤岩试件的总面积表示为Sz，煤岩界面轨迹识别结果的煤层残余量为Sc,岩层侵蚀量表示为Sq，则煤岩界面的识别精度表示为(Sz-Sc-Sq)/Sz×100%。

图17 煤层残余量与岩层侵蚀量定量分析Fig.17 Quantitative analysis of coal residual and rock erosion

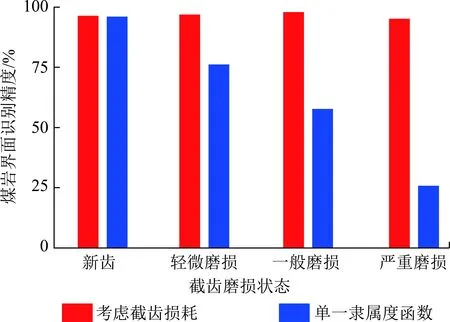
图18 截齿不同磨损状态识别精度对比分析Fig.18 Recognition accuracy comparison for different wear degree of picks

图18为考虑截齿损耗与未考虑截齿损耗的煤岩识别结果精度对比，可以看出，在新齿状态下，2种工况的识别精度基本处于持平状态，而随着截齿磨损程度的加剧，基于单一优化隶属度函数的煤岩界面识别结果精度明显降低，而考虑截齿损耗的煤岩界面识别方法，根据截齿的磨损状态，自适应的选择对应的优化隶属度函数，从而能够持续得到高精度的识别结果。

4.2 工业性实验结果与精度分析

为了验证构建的考虑截齿损耗的多信息融合煤岩界面感知识别模型的识别精度，开展现场工业性实验，根据相似原则浇筑工业实验煤壁。煤壁全长70 m，宽4 m，高3 m，其中主要部分以煤炭为主，硬度为F3，局部煤壁添加沙子、水泥以及特殊骨料等，硬度为F5，表示煤层中局部分布的岩层，整个煤壁物理结构特性与所选定煤矿非常接近。浇筑的岩层共分为2部分，一部分为水平走向分布岩层，一部分为随机走向分布岩层，水平走向分布岩层为等高1.5 m的线性平直岩层，用于截割过程中提取不同截煤比的特征样本信号，建立煤岩截割特征样本数据库，获取各特征信号的优化隶属度函数;随机走向分布岩层用于验证识别模型的精确性和可靠性，其随机走向分布的岩层在煤壁中的分布如图19所示，岩层全长9 m，厚度为1.2 m，最大高度为2.7 m。

图19 随机走向岩层分布Fig.19 Distribution of random rock stratum

实验采用的采煤机型号为MGN500/1130-WD，双滚筒采煤机，滚筒直径为1 800 mm，截割深度为 800 mm，适用于采高为1 800～3 860 mm的硬或中硬煤层。分别采用新齿、轻微磨损、一般磨损和严重磨损4种状态下的截齿截割浇筑的煤壁，截割过程如图20所示。测试过程中采煤机牵引速度为15 m/min，采煤机滚筒中心高度为 1 800 mm，截割深度为600 mm。结合实验室实验的对比分析方法，分别得到考虑截齿损耗及基于单一优化隶属度函数的煤岩界面识别精度，见表3。由表3可知，截齿损耗对煤岩截割特征信号的影响显著，截齿不同磨损程度状态下，如果采用单一的隶属度函数进行计算、融合与识别，识别精度差异性显著，而根据截齿的实际磨损程度，匹配对应的隶属度函数，能够保证持续、高精度的煤岩界面识别结果，为采煤机截割提供精准的煤岩界面轨迹。