扇形喷嘴射流行为的数值模拟研究
2021-07-15
(1.辽宁石油化工大学 石油天然气工程学院,辽宁 抚顺 113001; 2.中国石油天然气股份有限公司辽宁销售仓储分公司 设备工程部,辽宁 沈阳 110000)
随着水射流技术的发展,高压水射流技术已广泛应用于工业清洗、除锈与机械切割等工艺中[1-3]。喷嘴作为水射流工艺中转化射流能的主要元件,其性能的好坏直接影响着高压水射流技术的实际应用[4]。喷嘴按形状可分为针形喷嘴、扇形喷嘴和异型喷嘴等,其中扇形喷嘴由于其喷嘴形状可以产生平坦均匀的扁平射流,射流致密性好,而且射流扩散角变化范围很广,因此成功应用于高压水射流中[5-6]。任小增通过实验方法研究了扇形喷嘴的射流特性及磨损行为,分析讨论了扇形喷嘴磨损的影响因素和减磨措施[7]。欧阳联格等研究了非结构参数如入口压力、靶面距离和倾斜角度对射流特性的影响,解决了高压扇形喷嘴的非结构参数的匹配问题[8]。Jeffery和Joshua等采用实验方法对扇形喷嘴射流的运动特性和稳定性进行了研究[9-10]。
本文以扇形喷嘴射流行为为研究对象,采用数值模拟方法,研究不同参数如扇形喷嘴入口压力、收缩角(入口直径)、V型切槽半角对扇形喷嘴射流行为的影响,得到不同参数对扇形喷嘴内部及外部射流特性的影响规律,研究结果对扇形喷嘴的设计具有一定的指导意义。
1 模型建立
1.1物理模型
扇形喷嘴结构示意图如图1所示,其中影响性能的主要参数包括收缩角β、入口直径D、射流出口段直径d、射流出口段长度和V型切槽的半角α。本文假设扇形喷嘴收缩段长度L和射流出口段直径d为恒定值,通过改变喷嘴入口直径D来调节扇形喷嘴的收缩角度。为了分析不同参数变化对扇形喷嘴射流特性的影响,表1给出了本文数值模拟研究的主要参数和扇形喷嘴结构参数。
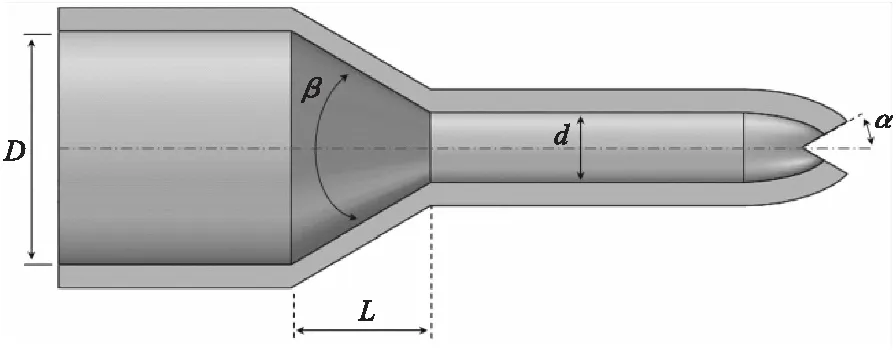
图1 扇形喷嘴结构示意图

表1 数值模拟参数及数值
1.2数学模型
1.2.1控制方程
由于扇形喷嘴射流过程属于湍流,故采用三维Navier-Stokes方程作为数值模拟求解过程的控制方程,并用标准k-ε湍流模型建立封闭控制方程组。
不可压缩流体的连续性方程:
(1)
动量方程:
(2)
湍动能k方程:
(3)
湍动能耗散率ε方程:
(4)
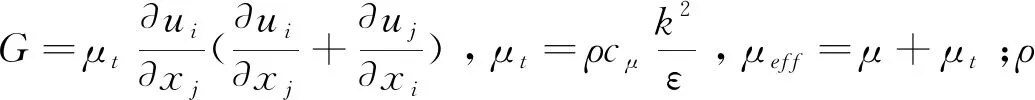
1.2.2边界条件及网格划分
扇形喷嘴及射流区的边界条件设置如图2所示。扇形喷嘴入口设置为压力入口,设定水的体积分数为1,即初始状态喷嘴内部充满水;出口设置为压力出口,压力值设为1个大气压;喷嘴内壁设置为壁面,其他喷嘴外部区域均设置为压力出口。外流场区域的长度设置为0.5 m。由于扇形喷嘴内流体区域结构比较复杂,因此本文采用四面体网格和六面体网格相结合的方式对整个流体区域进行网格划分。其中,喷嘴内部和射流冲击区采用六面体网格划分,喷嘴出口处采用四面体网格进行划分,计算区域网格划分如图3所示。整个流体区域划分网格的总数量约为118万。

图2 扇形喷嘴及射流区的边界条件设置
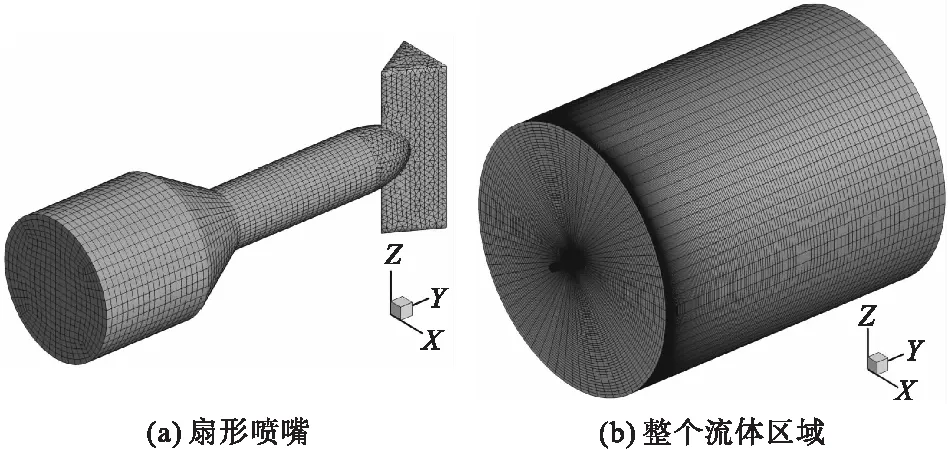
图3 扇形喷嘴和整个流体区域网格划分
1.2.3 求解过程
本文计算过程中压力-速度耦合算法采用Coupled,对于梯度、压力、动量和体积分数的空间离散,分别采用Least squares cell based、PRESTO、Second order upwind和GeoFraction方法。当连续方程的质量源项和各速度分量的相对残差值小于1.0×10-4时认为收敛。数值模拟过程中采用VOF(Volume of Fluid,简称VOF)两相流模型模拟气-水两相相互作用,其中空气设置为主相,水设置为第二相。
2 数值模拟结果及分析
2.1 入口压力的影响
在扇形喷嘴结构参数固定的条件下,入口压力的大小对扇形喷嘴射流特性影响很大。本文分别对入口压力P为5、10和15 MPa的扇形喷嘴射流特性进行仿真分析。图4~图6分别给出了不同入口压力条件下YOZ截面(视线垂直于V型槽)、XOY截面(视线平行于V型槽)和XOZ截面(压力出口)内扇形喷嘴射流的速度云图。其中,喷嘴入口直径D为8 mm,V型切槽半角α为30°。由图4可知,高压的水通过扇形喷嘴出口后,在YOZ截面内形成了扇形分布的射流。随着入口压力的增加,扇形喷嘴射流核心区的最大速度显著增大,入口压力为5、10和15 MPa时的最大速度分别达到了96、134和166 m/s,且在距离喷嘴0.5 m处的射流冲击宽度(沿Z方向的冲击宽度)略有增加。图5为XOY截面内速度云图,此时高压水经过扇形喷嘴后在XOY截面内形成一个冲击宽度很窄的带状射流,且随着入口压力的增加,扇形喷嘴射流核心区的最大速度增加。图6给出了压力出口处(XOZ截面内)速度分布云图。由图6可知,高压水经过扇形喷嘴后在压力出口截面内形成了沿X方向冲击宽度很小,而沿Z方向冲击方向很宽的狭长带状射流区域。同时可以看出,随着入口压力增加,扇形射流沿Z方向的冲击速度增大,冲击宽度变化不显著。

图4 不同入口压力条件下YOZ截面内速度云图

图5 不同入口压力条件下XOY截面内速度云图

图6 不同入口压力条件下XOZ截面内速度云图
图7(a)和图7(b)分别为YOZ截面内射流核心处和距扇形喷嘴出口Y=0.1 m处水的速度分布。由图7(a)可知,高压水经由扇形喷嘴喷出过程中,水的流速实现了两次加速过程。第一次加速发生在喷嘴收缩段处,由于喷嘴截面变小,在拐角处水的流速达到最大值;此后,水在扇形喷嘴圆柱段内持续加速,在喷嘴出口处随着截面收缩实现第二次加速。由图7(b)可知,在距扇形喷嘴出口Y=0.1 m处,随着入口压力的增大,水的流速最大值由87 m/s增加至152 m/s。
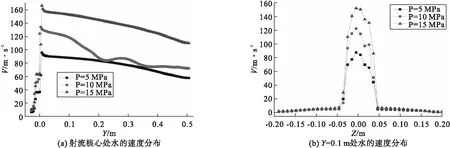
图7 不同入口压力条件下水的速度分布
2.2 入口直径的影响
图8~图10分别给出了不同入口直径D条件下YOZ截面、XOY截面和XOZ截面(压力出口)内扇形喷嘴射流的速度云图。其中,喷嘴入口压力P为10 MPa,V型切槽半角α为30°。由图8~图10可知,入口直径D变化对扇形喷嘴外流场区域射流特性影响并不明显。随着入口直径的增加,扇形喷嘴射流核心区域(外流场区域)流速最大值先减小后增加,其最大值分别为134.2、131.6和134.0 m/s。

图8 不同入口直径条件下YOZ截面内速度云图

图9 不同入口直径条件下XOY截面内速度云图

图10 不同入口直径条件下XOZ截面内速度云图
入口直径D变化主要影响的是扇形喷嘴内部射流特性。图11给出了不同入口直径条件下扇形喷嘴内部速度分布云图。由图11可知,由于扇形喷嘴入口直径D的改变,喷嘴圆柱段内的速度发生了显著变化。当入口直径较小时,速度最大值区域主要集中在喷嘴圆柱段中心;当入口直径增加至8 mm时,速度最大值区域向喷嘴圆柱段壁面处扩大;当入口直径增大至10 mm时,速度最大值区域又向喷嘴圆柱段中心集中。

图11 不同入口直径条件下扇形喷嘴内部速度云图
图12(a)和图12(b)分别为YOZ截面内射流核心处和距扇形喷嘴出口Y=0.1m处水的速度分布。由图12可知,与改变入口压力相比,改变入口直径D后,水由扇形喷嘴出口进入到外流场区域后,随着入口直径的增加,沿Y方向上的速度值衰减很快;沿Z方向上,在Y=0.1 m处射流核心处流速最大值变化并不明显。
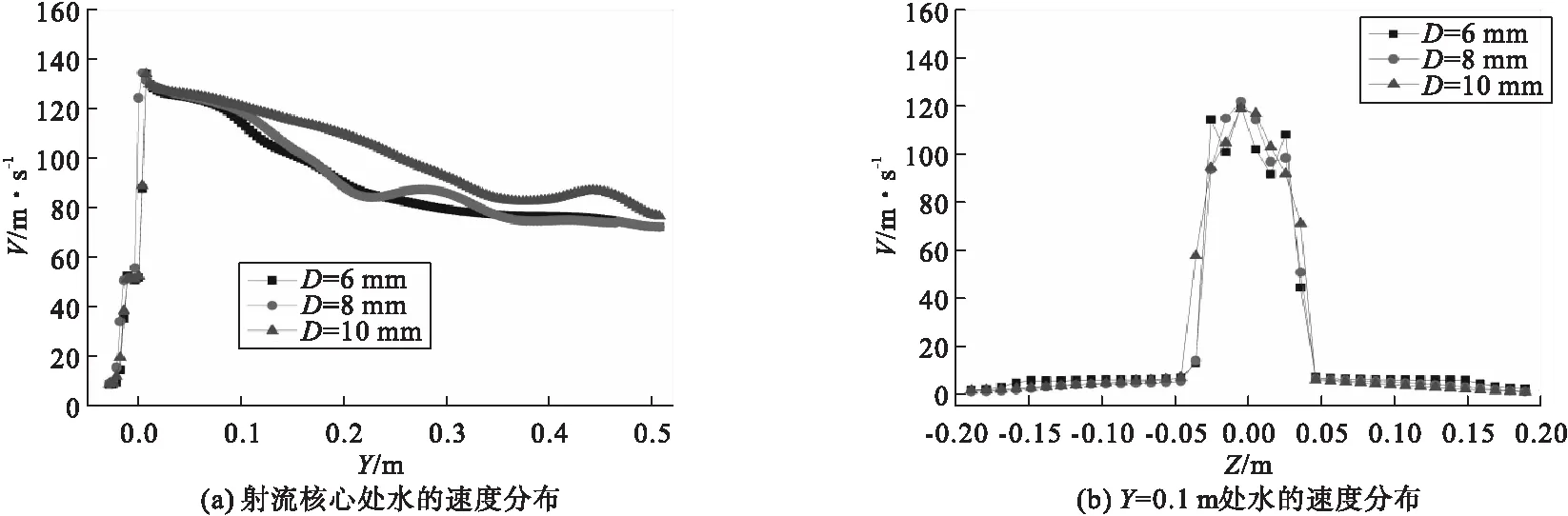
图12 不同入口直径条件下水的速度分布
2.3 V型切槽半角的影响
图13~图15分别给出了不同V型切槽半角条件下YOZ截面、XOY截面和XOZ截面内扇形喷嘴射流的速度云图。其中,喷嘴入口压力P为10 MPa,入口直径D为8 mm。由图13和图14可知,当V型切槽半角由30°增加至60°时,YOZ截面内扇形喷嘴射流核心区域内速度最大值由134 m/s增加至 139 m/s。XOY截面内速度变化不显著。由图13和图15可知,V型切槽半角的增加显著降低了扇形喷嘴射流的冲击宽度,且射流冲击区域内速度显著增加。当V型切槽半角由30°增加至60°时,扇形喷嘴射流的冲击宽度由0.34 m降低至0.12 m。

图13 不同V型切槽半角条件下YOZ截面内速度云图

图14 不同V型切槽半角条件下XOY截面内速度云图

图15 不同V型切槽半角条件下XOZ截面内速度云图
图16(a)和图(b)分别为YOZ截面内射流核心处和距扇形喷嘴出口Y=0.1 m处水的速度分布。由图16(a)可知,当V型切槽半角为30°时,外流场区域内水的流速衰减显著;当V型切槽半角逐渐增大时,外流场区域内水的流速衰减强度减弱。由图16(b)可知,当V型切槽半角由30°增加至60°时,距扇形喷嘴出口Y=0.1 m处水的速度最大值由122 m/s增加至133 m/s。由此可知,V型切槽半角减小有利于增大扇形喷嘴射流的冲击宽度,降低水的冲击速度。
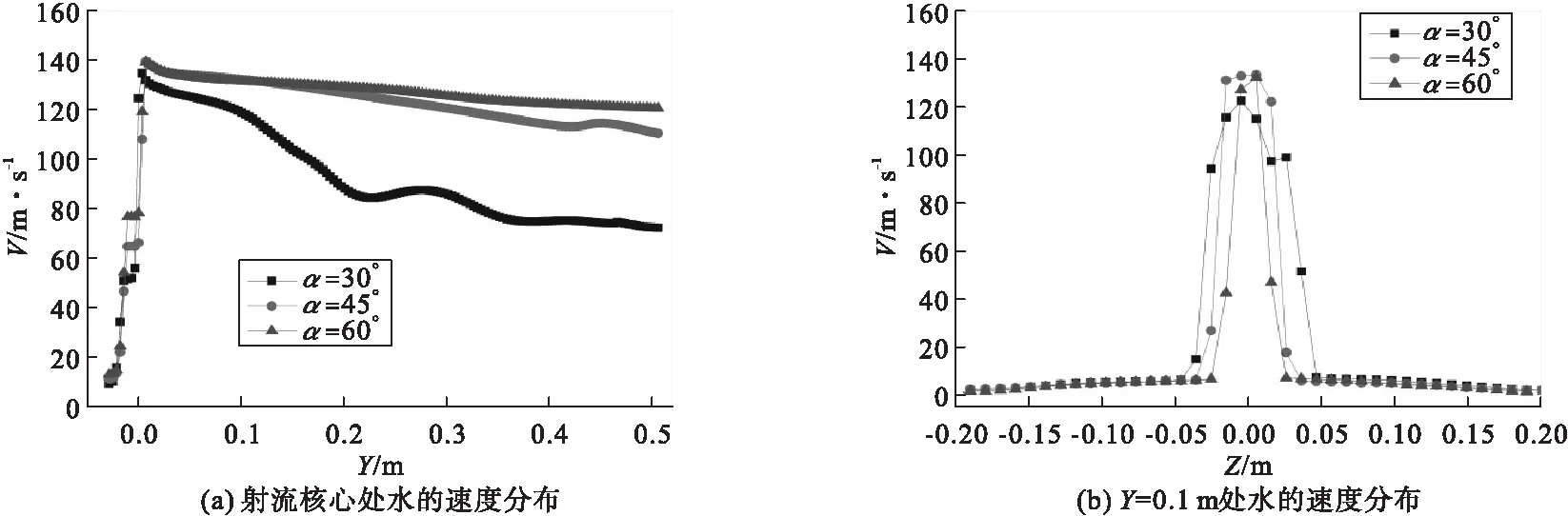
图16 不同V型切槽半角条件下水的速度分布
3 结 论
本文以高压扇形喷嘴射流行为为研究对象,采用数值模拟方法对不同的入口压力、入口直径(收缩角)和V型切槽半角条件下扇形喷嘴特性进行分析,得到以下结论:
(1)扇形喷嘴的主要参数,即入口压力、入口直径(收缩角)和V型切槽半角对扇形喷嘴内部及外部流场均具有一定的影响,各参数的变化对扇形喷嘴射流特性起着十分重要作用。
(2)入口压力和V型切槽半角对扇形喷嘴外流场影响显著。在本文参数范围内,增大入口压力可显著增加射流冲击核心区域内水的速度,但射流冲击宽度变化不显著;增大V型切槽半角可显著减小射流的冲击宽度,但射流核心区内水的流速显著增大。
(3)在本文参数范围内,扇形喷嘴入口直径(收缩角)的增加对外流场区域内射流特性影响不明显,但却显著改变了喷嘴内部的流动特性。
