盘式电机气隙漏磁与空载气隙磁密的解析计算

于慎波， 江爽， 夏鹏澎

(沈阳工业大学 机械工程学院，沈阳 110870)

0 引 言

轴向磁场盘式永磁电动机因其具有高转矩惯量比，结构紧凑，效率高，功率密度大等优点，因此适用于电动汽车驱动，新能源发电等领域。

在盘式永磁电机的分析与设计阶段，可以利用有限元软件进行仿真分析，但仿真过程需要较长的时间进行，这时候就需要用到解析法对盘式永磁电机进行初步分析。不管何种结构电机，该电机的漏磁系数与空载气隙磁密都是对该种电机进行初步分析需要考虑的。等效磁网络法是一种将磁路问题转化为电路问题来进行分析的方法。其中，等效磁网络模型中的电阻代表磁阻，电流代表磁通，电动势代表磁动势。这种方法对于轴向磁场、径向磁场、混合型磁场全都适用，相较于磁网络法来说，解析建模过程更加简单而且便于理解；相较于有限元法来说，不需要对复杂的电机本体进行实体建模，能更快高效地解决问题。文献[1]采用该方法对一台径向磁场永磁电机进行了分析，计算了电机在不同气隙长度,不同极距和不同剩磁密度下的气隙磁密及漏磁系数，并且经过了有限元仿真计算的验证，但该文献没有考虑端部漏磁。文献[2]采用该种方法分析计算了单定子单转子轴向磁场盘式电机不同气隙长度和极弧系数下的漏磁系数，并且经过了有限元仿真计算的验证，该文献考虑了端部漏磁。文献[3]计算了横向磁通永磁直线电机定转子在不同位置下的气隙磁导，由此建立了该电机变磁导等效磁网络模型，基于此模型解析计算出电机的空载反电势。文献[4]建立了无刷双馈电机的等效磁网络模型，基于此模型分析了电机在不同工况下的运行特性，并通过实验进行了验证。文献[5]采用精确子域模型法解析计算了一台10极12槽不等宽不等厚Halbach部分分段径向永磁同步电机的空载气隙磁密，并且考虑了齿槽效应。文献[6-8]给出了空载气隙磁密分布解析公式，利用此公式可以直接算出轴向磁通永磁电机任何位置的空载气隙磁密的大小。该公式由三部分组成：永磁体产生的气隙磁密、齿槽效应函数、端部效应修正函数。文献[9]基于一个永磁直线电机模型，介绍了一个基于傅里叶分析的永磁体产生的气隙磁通密度分布方程。文献[10]完全利用二维有限元进行曲线拟合出轴向磁通永磁无刷直流电机的端部效应函数曲线，并将平均半径处的气隙磁密曲线利用有限元与解析算法进行对比，结果比较吻合。文献[11]在文献[10]的基础上提出了利用虚拟等效直线电机模型的概念推导端部效应修正函数解析公式。本文首先对盘式电机的磁路进行了分析，解析求出气隙磁场中的各种漏磁磁阻，提出利用等效磁网络法求解盘式电机气隙漏磁系数。通过函数的变形并利用二分法优化计算去求解该种电机端部效应修正函数，并利用解析法求解考虑开槽效应的平均半径处的空载气隙磁密。最后，通过有限元法进行了对比验证。

1 轴向磁场盘式永磁电机等效磁网络模型

轴向磁场盘式永磁电机结构示意图如图1所示。电机模型参数如表1所示。该电机额定功率为5 kW，额定转速为450 r/min。

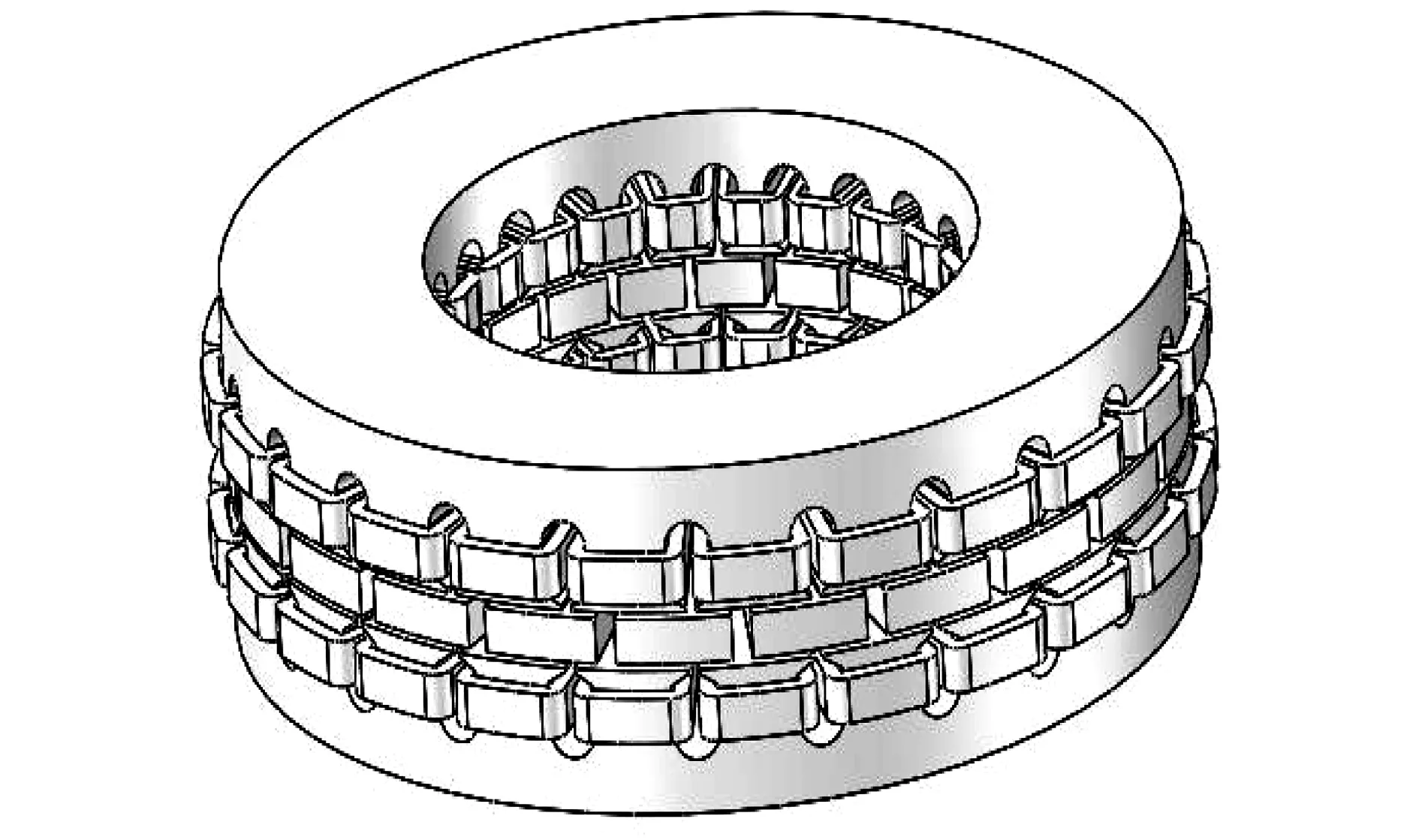
图1 盘式永磁电机结构示意Fig.1 Construction of disc PM motor

表1 电机参数

由于盘式电机的对称性，在对电机的磁路进行分析时，不需要对整机的磁路进行分析，只需在一个极距单元来进行分析。如图2所示为一个极距单元下的盘式电机磁路模型图。其中，回路①表示气隙主磁通，回路②表示永磁体边缘漏磁磁路(分为3种情况漏磁，分别是沿永磁体圆周方向漏磁，沿永磁体内圆周边缘漏磁，沿永磁体外周边缘漏磁)，回路③表示相邻永磁体之间的漏磁磁路。由图2所示的盘式电机磁路图可以得到如图3所示的盘式电机等效磁网络图。在图3中，Φr为永磁体虚拟内禀磁通，Φm为永磁体向外磁路提供的总磁通，Φg为气隙主磁通，Rg为气隙磁阻，Rc为电枢电阻，Rm为永磁体自身磁阻，Rmo为永磁体外周边缘漏磁，Rmi为永磁体内周边缘漏磁磁阻，Rmr为永磁体沿圆周方向漏磁磁阻，Rmm为相邻永磁体之间漏磁磁阻，Fad为电枢反应产生的电动势。

图2 盘式永磁电机磁路模型Fig.2 Magnetic circuit model of disc PM motor

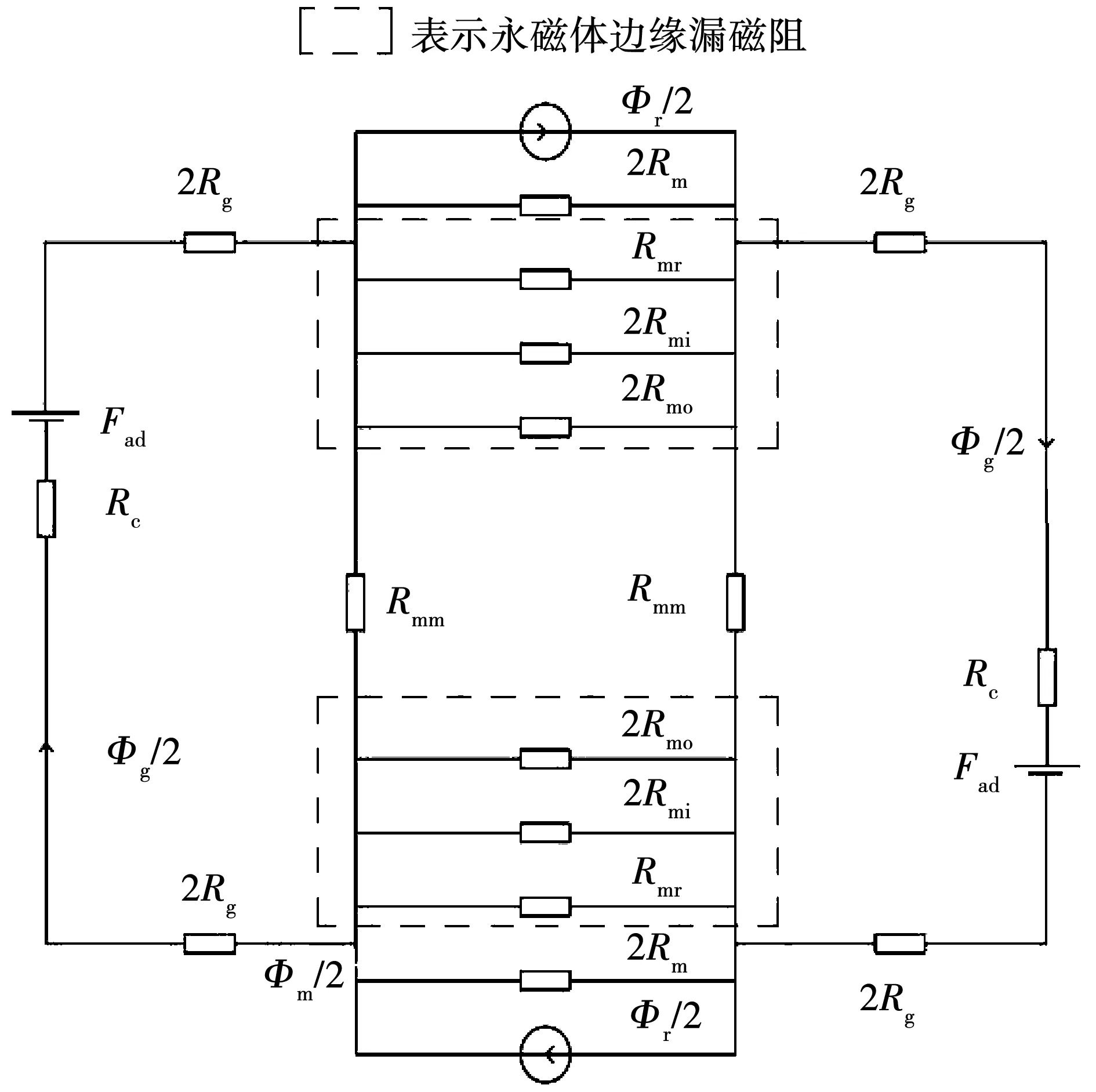
图3 盘式永磁电机等效磁路网络Fig.3 Equivalent magnetic circuit of disc PM motor

考虑到磁路对称性，可以将图3简化为图4。在对模型进行简化时，可以认为Rc=0，Fad=0。

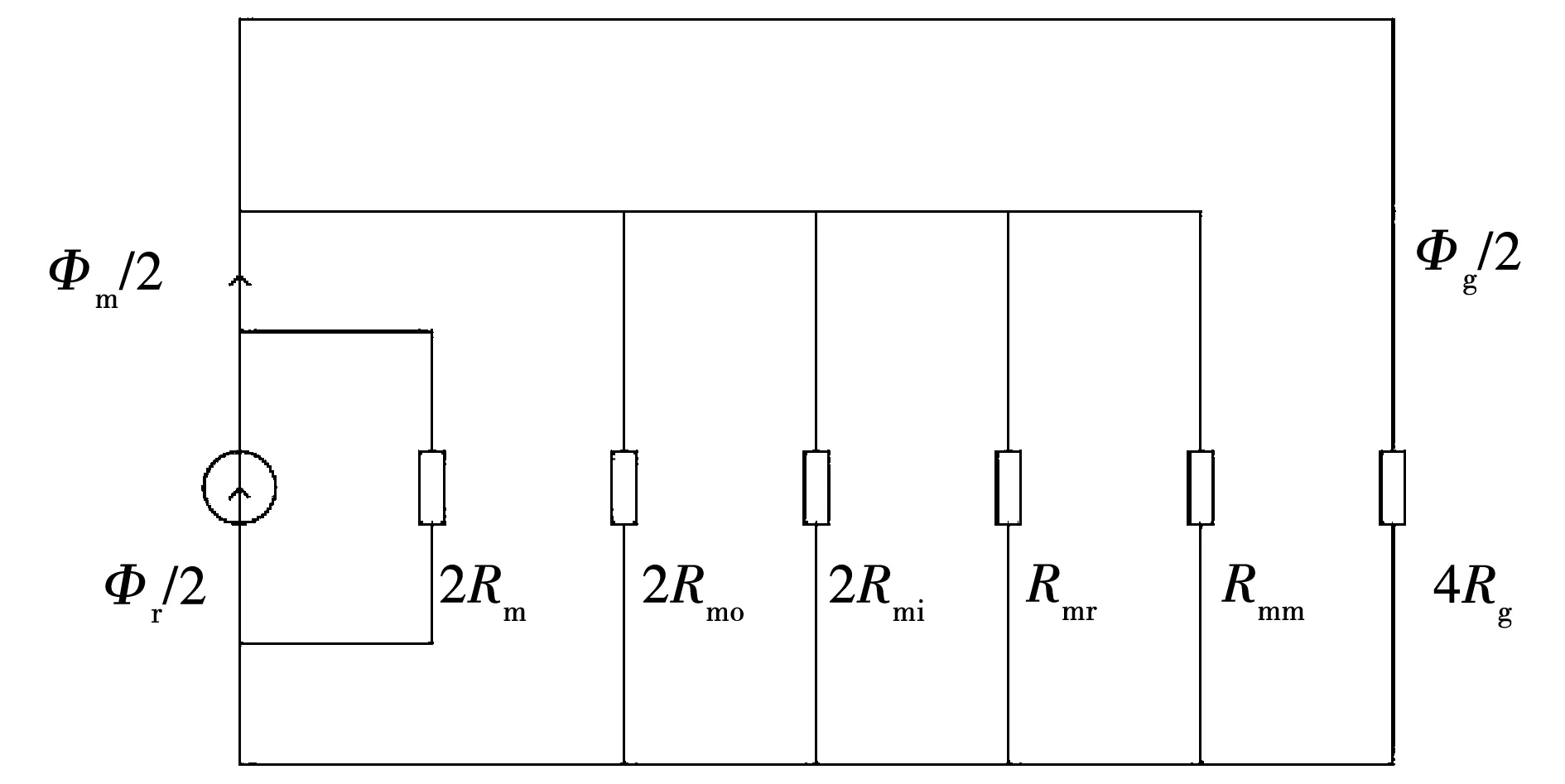
图4 盘式永磁电机简化磁网络Fig.4 Reduced magnet circuit of disc PM motor

根据图4所示的简化等效磁路网络图，可以得到：

(1)

(2)

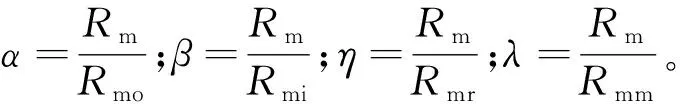
(3)

平均气隙磁通密度为

(4)

式中：Ag为气隙面积；Am永磁体轴向面积；αp为极弧系数。

2 各部分磁阻的计算

2.1 永磁体内磁阻Rm以及气隙磁阻Rg

永磁体内磁阻Rm和气隙磁阻Rg可以表示为：

(5)

(6)

(7)

(8)

式中：Am为每极永磁体的充磁方向截面积；Aeff为考虑边缘效应时每极气隙有效截面积；hm为永磁体厚度；μ0为真空磁导率；μr为永磁体相对磁导率；αp为极弧系数；p为极对数；Dmo为永磁体外直径；Dmi为永磁体内直径；g′为考虑开槽效应后的气隙长度。

由于存在开槽效应，在槽口处的气隙长度会发生变化，所以需要用卡特系数kc去表示实际气隙长度g′。卡特系数kc计算方法[9]为：

(9)

g′=kcg。

(10)

式中：ωs定子齿宽；τs为槽距。

2.2 其他漏磁磁导的计算

文献[12]介绍了如何利用圆弧直线法求解双气隙电机漏磁磁导，由此我们可以直接得到电机的其他漏磁磁导。

永磁体内周边缘漏磁磁导可以表示为

(11)

永磁体外周边缘漏磁磁导可以表示为

(12)

本文使用的电机两永磁体极间距离的一半大于气隙长度，因此永磁体沿圆周方向漏磁磁导可以表示为

(13)

相邻永磁体之间漏磁磁导可以表示为

(14)

将式(11)到式(14)表示的磁导分别求倒数，即可得到各自的漏磁磁阻。

3 空载气隙磁密解析

在对电机进行空载气隙磁密数学模型的建立时，当考虑齿槽效应和端部效应的情况下，半径r处的空载气隙磁密可表示为[7]

B(r,θ)=Bslotless(r,θ)ξ(r,θ)τ(r)。

(15)

式中：Bslotless(r,θ)表示忽略齿槽效应和端部效应时半径r处永磁体产生的气隙磁密；ξ(r,θ)表示考虑开槽的相对气隙磁导函数；τ(r)表示考虑定子极外半径和内半径附近端部效应的端部效应修正函数。

Bslotless(r,θ)=

(16)

式中：n为气隙磁密谐波次数；αp(r)为半径r处的极弧系数。对于常规扇形永磁体，αp(r)=αp。

3.1 端部效应修正函数τ(r)解析

端部效应修正函数τ(r)的表达式为[8]

(17)

(18)

式中：Ro为定子外半径；Ri为定子内半径；ψ为与电机参数相关的参数。

如图5为有限元法仿真得到的磁极中心线气隙磁密图，由图可以看出在径向距离为80～115 mm范围内气隙磁密保持不变，即τ(r=80～115 mm)=1，取r=85代入式(18)，分析得出ψ的取值范围为1≤ψ≤4。利用二分法优化计算，取ψ=1、2、3、4，得到图6。取ψ=1.7、2、2.3，径向位置取72～82 mm,得到图7。从图7中可以看出ψ=2为最佳值。

图5 磁极中心线气隙磁密曲线图Fig.5 Air gap flux density in the radial center line of one pole

图6 ψ分别取1、2、3、4时磁极中心线气隙磁密与有限元仿真对比图Fig.6 Comparison of air gap flux density in the radial center line of one pole between FEM and analytical method when ψ is taken as 1,2,3,4

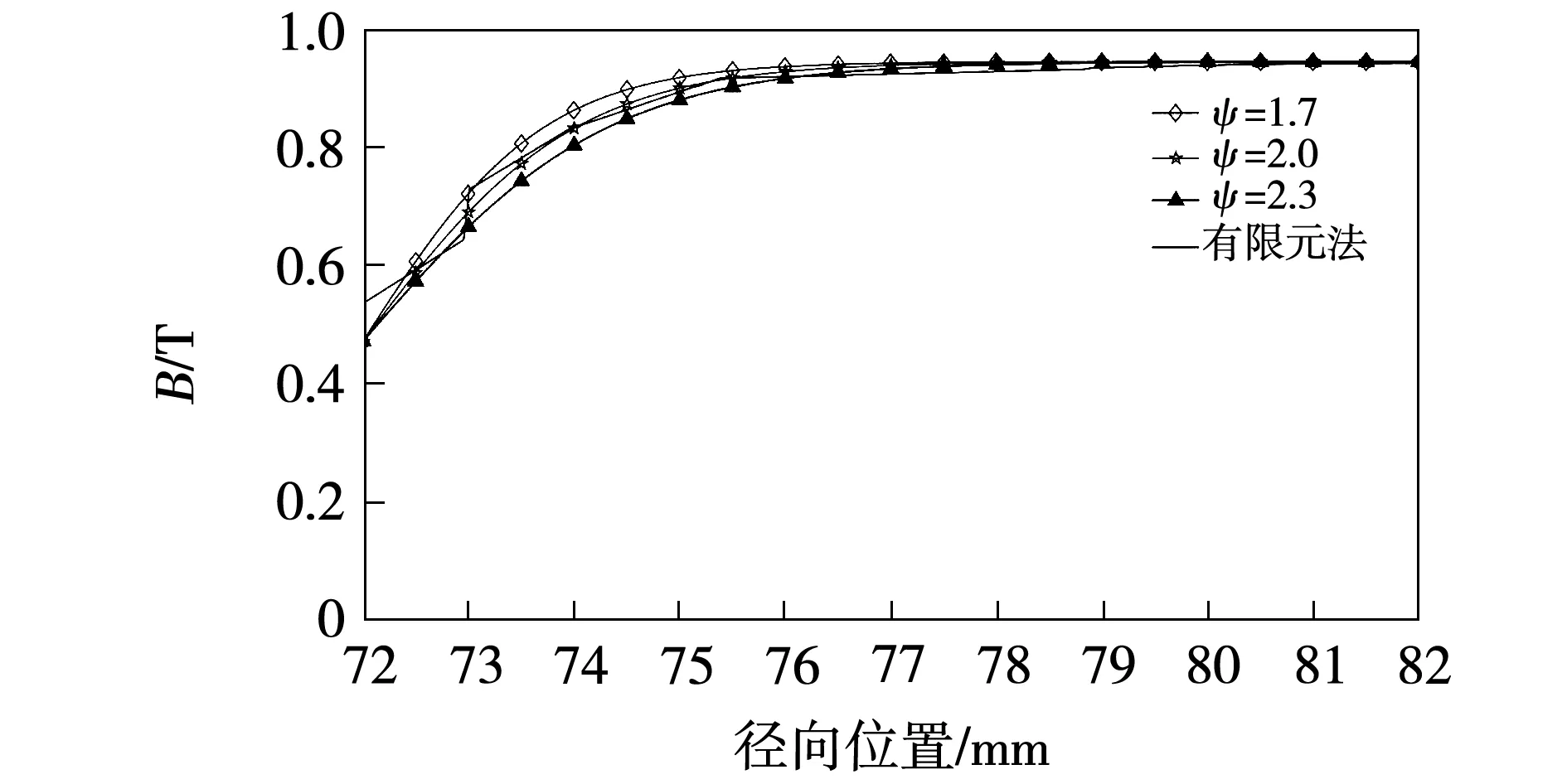
图7 ψ分别取1.7、2、2.3时磁极中心线气隙磁密与有限元仿真对比图Fig.7 Comparison of air gap flux density in the radial center line of one pole between FEM and analytical method when ψ is taken as 1.7,2,2.3

由此可以得出盘式永磁电机的端部效应修正函数曲线如图8所示。

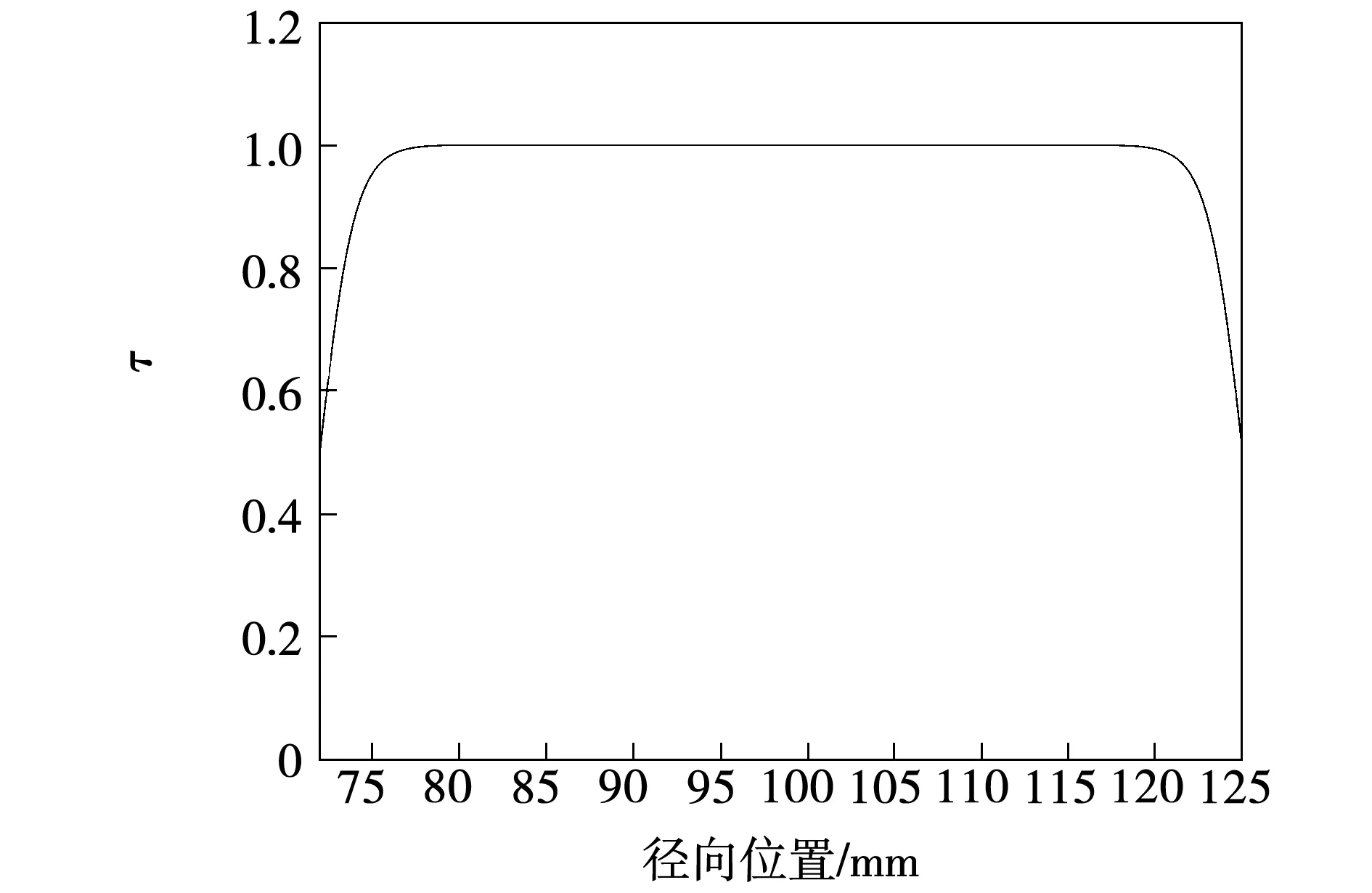
图8 端部效应修正函数曲线Fig.8 Analytical results for end effect correction function

3.2 考虑开槽的相对气隙磁导函数ξ(r,θ)解析

定子开槽会导致槽口部分的气隙磁密发生变化，这是由于槽口区域的气隙长度大于非槽口区域的气隙长度，从而使得槽口部分的气隙磁阻大于非槽口区域的气隙磁阻。文献[13]给出了气隙中和槽口部分的磁通路径的求解方法：将其分别等效为平行直线与四分之一圆弧。

文献[11]给出了一个槽距内考虑开槽的相对气隙磁导函数，在此基础上，扩展到24个槽距内考虑开槽的相对气隙磁导函数，即

(19)

(20)

其中：k=0，1，2，…，23；b0表示槽口宽度。将式(20)代入到式(19)中，得到平均半径处考虑开槽的相对气隙磁导函数曲线，如图9所示。

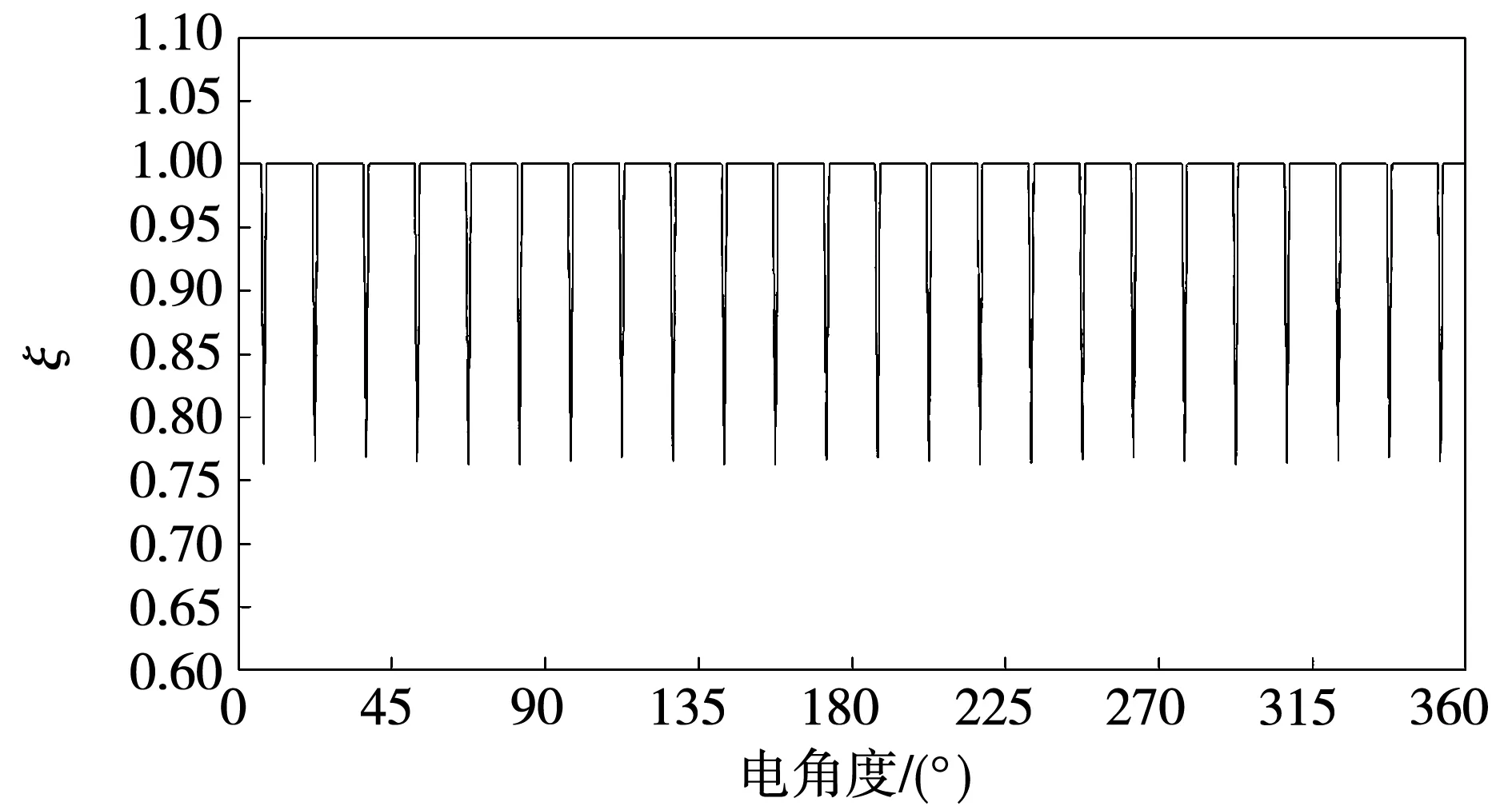
图9 平均半径处考虑开槽的相对气隙磁导函数曲线Fig.9 Relative air gap permeance function curve considering slotting at average radious

4 有限元仿真验证

本文以一台22极24槽轴向磁场盘式永磁电机为例, 首先是针对盘式永磁电机进行三维建模。在针对盘式电机的空载气隙磁场进行有限元仿真分析时，永磁体的充磁方向的设置是沿轴向的。对于永磁体的充磁方向具体在软件中的设置就是：“N”极的“X，Y”方向设置为“0”，“Z”方向设置为“1”；“S”极的“X，Y”方向设置为“0”，“Z”方向设置为“-1”。图10给出了有限元仿真计算结果的空载情况下的三维磁通密度分布云图。如图11所示为盘式永磁电机三维气隙磁密图。

图10 空载下的三维磁通密度分布云图Fig.10 Three dimensional magnetic flux density distribution nephogram under no load

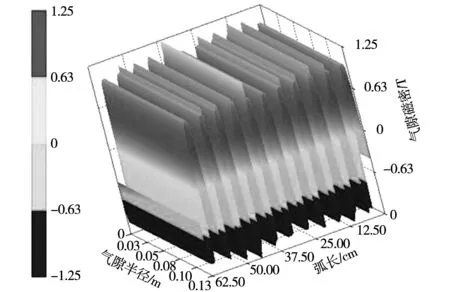
图11 盘式永磁电机三维气隙磁密图Fig.11 Three dimensional air gap flux density of disc motor

4.1 气隙漏磁系数和平均气隙磁密的验证

有限元法算出的气隙漏磁系数为1.139 7，而用等效磁网络法算出的漏磁系数为1.101 6，误差为3.34%。有限元法算出的平均气隙磁密为0.780 4 T，而用等效磁网络法算出的平均气隙磁密为0.751 8 T，误差为3.66%。

4.2 端部效应修正函数曲线验证

为验证验证本文所提出的端部效应修正函数，又选取了一个20极30槽，定子外径为200 mm，定子内径为128 mm的双定子单转子盘式电机，对其磁极中心线气隙磁密进行仿真，图12为有限元与解析法计算磁极中心线气隙磁密对比图。说明端部效应修正函数适用于不同尺寸、不同极槽配合、不同结构类型的轴向磁场盘式永磁电机。

图12 有限元与解析法计算磁极中心线气隙磁密对比图Fig.12 Comparison of air gap flux density in the radial center line of one pole between FEM and analytical method

4.3 平均半径处气隙磁密函数验证

当径向位置在平均半径处，τ(r)=1。图13是利用解析法和有限元法计算平均半径处的气隙磁密对比图。

从图13可以看出有限元与解析法对比的结果基本吻合，特别是在齿槽效应引起的气隙磁密发生突变的地方能较好的对应上，这说明了考虑开槽的相对气隙磁导函数是切实的。用有限元法算出气隙磁密的平均值为0.780 4 T，解析法算出的气隙磁密的平均值为0.761 1 T，误差为2.47%。综上，说明本文采用的解析法计算空载气隙磁密是可行的。

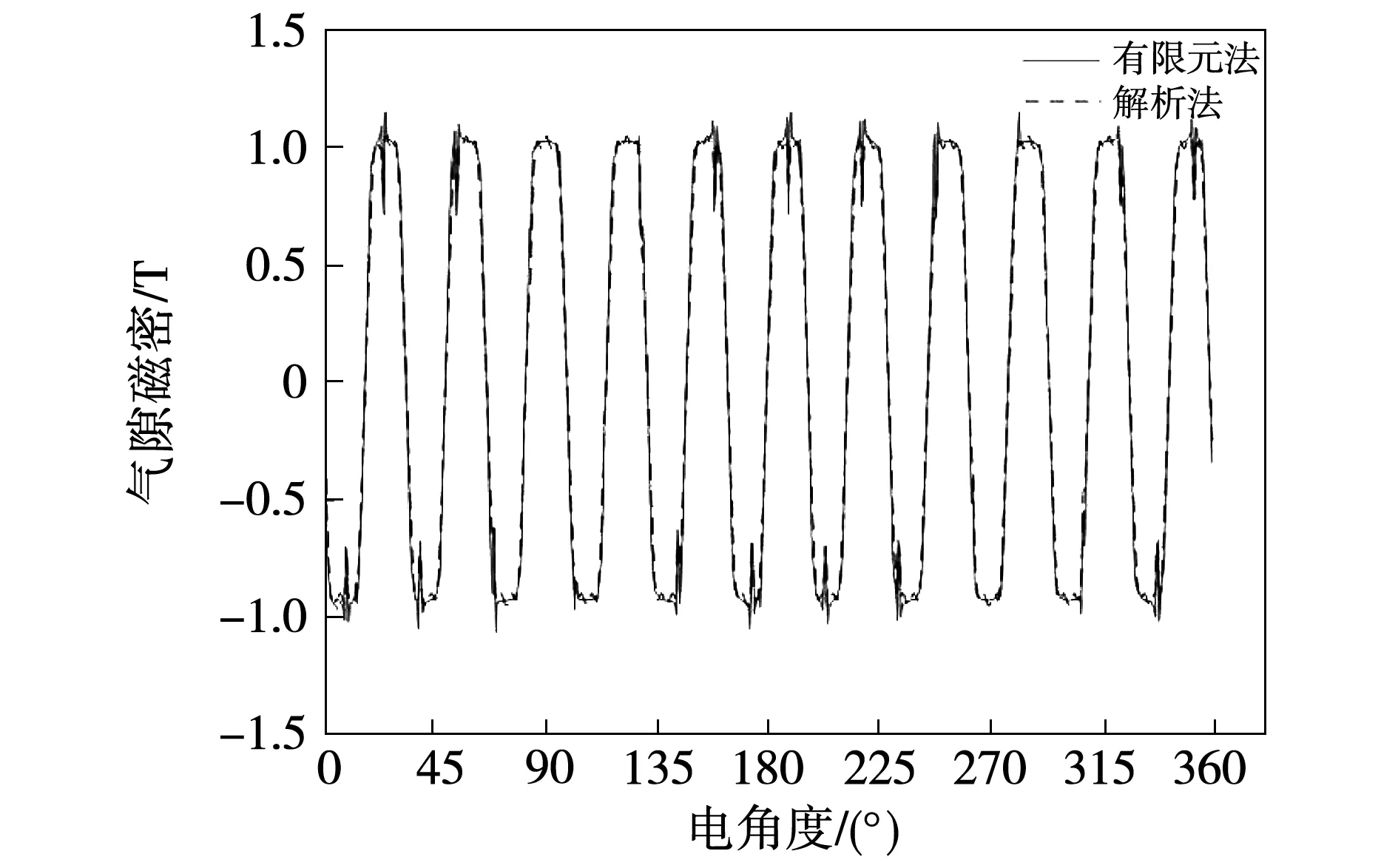
图13 有限元与解析法计算平均半径处气隙磁密对比图Fig.13 Comparison of air gap flux density at average radius between FEM and analytical method

5 结 论

本文针对一台22极24槽的轴向磁场盘式永磁同步电机，利用解析法与有限元法计算了气隙漏磁系数，端部效应修正函数，槽数为24槽的齿槽效应函数、完整的空载气隙磁密函数。

1)本文利用等效磁网络法建立了双定子单转子盘式永磁电机的等效磁路网络模型，利用圆弧直线法求出了该电机的各种漏磁磁阻，解析计算出气隙漏磁系数和平均气隙磁密，解析法与有限元法所计算的气隙漏磁系数和平均气隙磁密的误差分别为 3.34%和3.66%。

2)经过推导得出新的端部效应修正函数，然后运用二分法优化计算，确定了未知参数ψ，得到了解析法绘制的端部效应曲线图。推导出的端部效应修正函数适用于不同尺寸、不同极槽配合、不同结构类型的轴向磁场盘式永磁电机。

3)利用解析法计算出24个槽距下的相对气隙磁导函数和考虑齿槽效应的平均半径处的空载气隙磁密分布，并与有限元法得到的磁密曲线进行了对比，其气隙磁密的平均值的误差为2.47%。