基于液晶空间光调制器的复振幅全息显示进展

隋晓萌， 何泽浩， 曹良才， 金国藩

(清华大学 精密仪器系 精密测试技术及仪器国家重点实验室，北京100084)

1 引 言

三维显示作为信息呈现的重要手段，能够展现出物体位置关系与不同视角的信息，并让场景具有一定的深度感，是一种精确和真实的显示技术。目前较为广泛应用的视差型三维显示还存在分辨率低、视场角小、辐辏与调焦不匹配等不足，难以提供真实的三维感观，容易造成人眼视疲劳。全息显示技术通过记录和再现物光波的波前，可重建出具有深度信息的真三维图像，其加载的数据量大，符合人眼的观察习惯。全息显示技术与光电技术和计算机技术相结合，有广阔的应用前景与发展潜力，对制造业、医疗、军事、教育和娱乐等领域的发展有着重要的意义，是目前信息呈现领域的研究热点之一。

全息术(Holography)的概念在1948年由英国物理学家Dennis Gabor提出[1]。传统的全息技术包括记录和重建两个过程。记录过程是将相干光分束，一束作为物光照射需要记录的物体，一束作为参考光与物光发生干涉。物光波的振幅和相位携带着物体表面特征相关的信息，物光和参考光干涉产生的条纹则包含了物光波的振幅和相位信息并被记录在感光材料上。在重建过程中使用相同的光源照射感光材料，读出记录下的振幅和相位信息并重建出与原物相同的三维图像。

随着计算机技术与显示器件的发展，传统全息中的波前记录过程可以在计算机中实现，即计算全息技术(Computer-generated Holography，CGH)[2-3]。计算全息包含波前计算、波前编码与波前重建三个过程。通过数值计算的方法实现物光波的波前计算，得到该复振幅波前在全息图平面的数学描述，随后将全息图平面的复振幅分布编码为与显示媒介相匹配的全息图函数。在光学重建的过程中，全息图函数被转移至显示媒介，通过相干光照射显示媒介重建出物光波前[4-5]。传统显示媒介多为静态媒介，如透明玻璃板、衍射光学元件等。近年来，以液晶空间光调制器为代表的动态显示器件发展迅速，产生了空间光调制器实时调制入射光波的动态重建物光波前模式。

计算全息技术的优势主要表现在3个方面：(1)能够避免复杂的干涉记录光路，简化全息图的生成过程。波前计算只需获得全息图物光波前的数学表达，可生成真实物理世界不存在的物光波。(2)计算全息摆脱了记录介质的限制，全息图函数可以数字形式复制、储存和传输。(3)计算全息使计算机与数字化器件被引入光学处理与光学调控领域，开创了计算机介入光学过程的波前调控模式。因此计算全息在三维显示[6]、光学操纵[7]、光束整形[8]、光学加密[9]、光学激发[10]等方面具有广阔的应用前景。

空间光调制器作为全息图的承载媒介之一因其具备数字编码与动态调控能力而受到广泛关注，因此基于空间光调制器的全息显示一直是全息三维显示研究的关键内容[11-14]。但空间光调制器大多仅能实现单一振幅或相位调制，制约其在全息显示领域的深入应用。目前最为广泛应用的振幅型与相位型空间光调制器分别为数字微镜器件(Digital Micromirror Device, DMD)与硅基液晶(Liquid Crystal on Silicon，LCoS)。数字微镜器件是由多个小型反射镜面组成的高速光开关阵列，通过控制微镜的翻转频率实现对入射光场的振幅调控，多用于编码振幅型全息图。由于振幅型全息图的计算需在计算机中模拟生成物光波与参考光波的干涉光场并只保留振幅项，其重建时共轭像与原始物体同时重建，光能利用率低。相位型空间光调制器的设计与加工则主要基于硅基液晶技术，通过液晶排列层中液晶的旋向与入射光的偏振态实现相位调制。相位型全息图的生成需在计算机中模拟记录物体的衍射场，并仅保留衍射场相位使用均匀振幅重建。为使计算衍射场更加接近均匀振幅场，通常在计算时对记录物体添加随机相位使其高低频成分均能充分扩散，导致重建结果中产生散斑噪声。除此之外，由于空间光调制器调制动态范围和精度有限，全息图的实际显示能力无法达到理论的计算效果[15]。

随着高分辨率液晶空间光调制器与双相位的复振幅编码方法的发展，复振幅全息显示近来受到广泛关注。相比相位型全息图与振幅型全息图，复振幅全息具有一些显著优点：(1)高运算效率。为最大限度地利用空间带宽积，由复振幅波前转换为相位型全息图的过程大多依赖优化算法，计算耗时长。而复振幅全息图的振幅得以保留，不同空间频率的衍射场相对强度信息可通过振幅项表征。(2)高空间带宽积。复振幅全息图同时保留物光波前的振幅与相位，充分利用现有显示器件的空间带宽积，最大程度还原物光波的传播场。(3)高重建精度。复振幅全息图能够有效避免因振幅编码或相位编码而引入的重建噪声，如振幅型全息图的孪生像问题与相位型全息图的散斑问题[16]。基于上述优点以及近年来显示器件、编码算法与重建系统的发展，复振幅全息成为三维显示的重要发展方向。

本文从双相位的复振幅全息技术、相位干涉的复振幅全息技术以及空间光调制器级联调控复振幅全息技术等3个方面对基于液晶空间光调制器的复振幅全息的原理进行分类，对其研究进展进行概述，并对复振幅全息的发展提出了展望。

2 双相位全息图

2.1 双相位分解原理

1978年，Hsueh与Sawchuk 提出将任何复振幅量Aeiφ振幅归一化至0≤A≤1 后，均可分解成为两个具有相同均匀振幅的分量[17]：

(1)

其中α=cos-1A且0≤α≤π/2。由此得出，使用两个纯相位分量，可以合成复振幅场：

H=h1+h2=eiθ1+eiθ2，

(2)

即通过两幅相位型全息图的相干叠加，可恢复出全息图平面的复振幅场，如图1所示。

图1 均匀振幅圆内的复振幅分解原理Fig.1 Principle of complex modulation in the unite circle

基于双相位分解原理，演化出两种复振幅全息的编码思路。一种为将分解的双相位分量逐个像素穿插排列，使得相邻像素在衍射传播的过程中相干叠加，即双相位全息图。由于其双相位分量相干叠加时存在空间错位，需依靠空间滤波系统消除部分空间频率才能重建复振幅波前。另一种为将分解的双相位排布在不同空间光调制器或同一空间光调制器的不同区域，通过特定的光路设计使双相位分量干涉，即相位干涉复振幅重建。相位干涉的复振幅理论上可重建理想复振幅场，重建精度高，不依赖空间滤波。

2.2 早期的双相位全息图方法

双相位分解的方法被提出后，相位型全息图的加工与编码尚不成熟。Hsueh与Sawchuk将分解的双相位分量作为一个复振幅单元内的两个子单元，运用迂回相位[18-19]的方法进行相位编码(图2)。

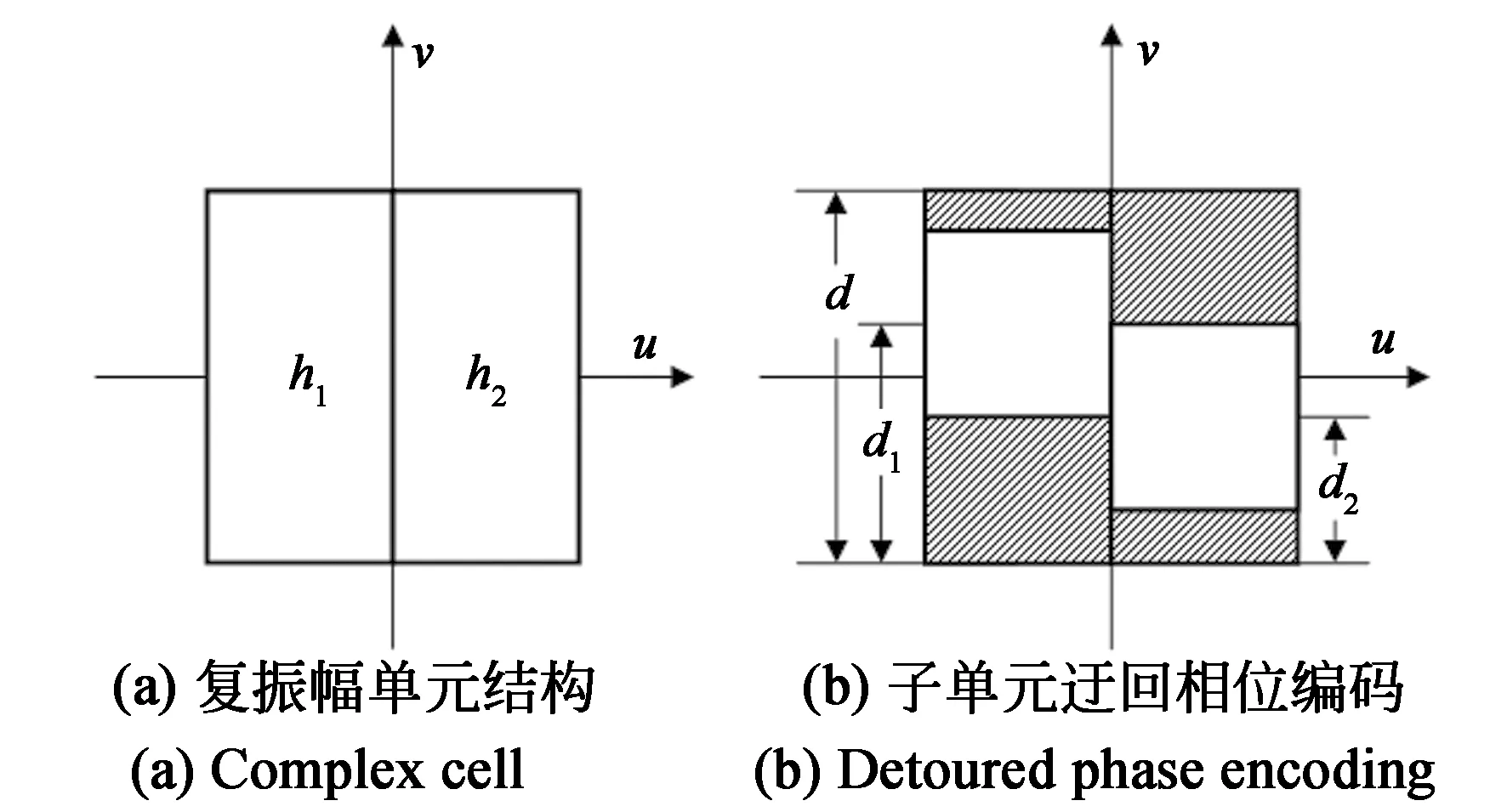
图2 迂回相位编码双相位全息图[17] Fig.2 Double-phase hologram encoded by detoured phase[17]

迂回相位编码的基本原理为在全息图调制单元内设矩形窗口，窗口内透过率为1，窗口外透过率为0。通过矩形窗口的参数调制复振幅场，矩形窗口的面积可编码振幅信息，矩形窗口的偏移量可编码相位信息。由于双相位分量具有相同均匀振幅，因此使用相同面积矩形窗的不同偏移量调制双相位的子单元：

d1=d(φ+α)/2π，

(3)

d2=d(φ-α)/2π.

(4)

经此编码后的全息图即为双相位全息图。以这种调制单元与子单元结构为基础的双相位编码方式在此后一段时间内占据主导位置，并对双相位的衍射光学元件(Diffractive Optical Element, DOE)设计产生了影响[20]。

2.3 空间光调制编码的双相位全息图

随着数字化调控器件的革新与发展，空间光调制器具备了对输入光场的相位像素化调控的能力，相位调制的分辨率与调制精度得到了突破性的提升，由此产生了将双相位全息图编码到空间光调制器上的复振幅全息调控方案，双相位分量在空间光调制器上的排布方式也成为相位型空间光调制器广泛应用以来的主要研究方向。这一时期内，随着对双相位全息图研究的推展，研究者们发现，影响双相位全息图重建质量的主要因素包含两方面：其一为双相位分量在全息图中空间排布错位，重建时带来了噪声；其二为针对相同采样数目的物光场，双相位全息图编码所需的像素数目更多，调制单元尺寸更大，因而重建时空间分辨率较低。因此，如何设计出具有最低错位噪声、最高空间分辨率与最简计算流程的双相位排布方式成为这一阶段内需要解决的核心问题。

1991年， Florence与Juday 将双相位全息图初步编码到相位型空间光调制器上[21]。在该工作中，双相位的排布方式仍保留了早期调制单元与子单元的结构，如图3(a) 所示，先由空间光调制器像素组成双相位分量的子单元，再由双相位子单元构成复振幅调制单元。该编码方法可以保证使用空降光调制器编码双相位后复振幅光场沿水平与竖直方向采样间隔仍保持一致，但一个复振幅调控单元占用像素数目过多，导致对全息图空间带宽积的利用率较低，重建场的空间分辨率较低。

2002年，Arrizón对复振幅单元结构进行改进[22]，双相位子单元改为左右分布的各一个像素，复振幅单元也相应变为了由两个像素组成的矩形单元(图3(b))。这一改进不仅极大地提升了空间分辨率，更简化了编码计算的复杂程度。但矩形复振幅单元结构对复振幅场沿水平与竖直方向上的采样间隔不一致，对其重建结果带来较大的影响。同年，Arrizón与Sanchez-de-la-Llave 对此进一步改进[23]，由4个像素组成复振幅单元如图3(c)，即为巨像素(Macro Pixel)，在一个复振幅单元内双相位分量沿对角线交错排列。该巨像素结构既能够保持全息图对复振幅场的水平与竖直方向采样间隔相等，同时通过不同方向的错位补偿，极大地减小了双相位全息图的错位噪声[24]。但由于该方法中一个复振幅的巨像素包含4个空间光调制器像素，双相位编码对复振幅光场进行了降采样，空间带宽积的利用率仍旧相对较低。

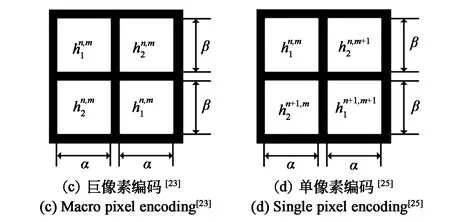
图3 空间光调制器的双相位编码方式Fig.3 Double-phase encoding on the spatial light modulator

2014年，Mendoza-Yero等人提出了一种单像素操作与采样的双相位编码方法[25]。将复振幅光场按照空间光调制器参数离散采样并依据双相位原理分解：

(5)

(6)

(7)

将分解后的双相位分量通过互补的二元光栅进行像素级采样，该二元光栅是透过率为0或1的像素棋盘格，采样后的双相位分量相加即为一幅相位型全息图：

(8)

其中θn,m可表示为：

θn,m=φn,m+(-1)n+mcos-1(An,m) .

(9)

图4为基于二元光栅采样的单像素双相位编码方法的计算流程。编码后的双相位全息图像素排布如图3(d) 所示，采样后的双相位分量交错分布。

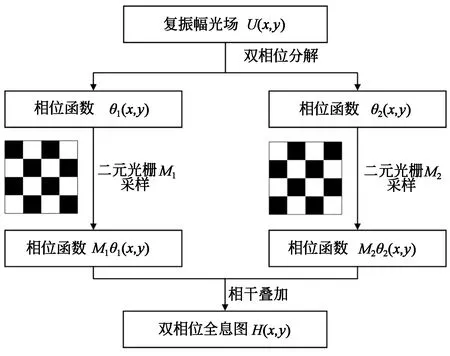
图4 二元光栅采样的双相位图编码流程图[25]Fig. 4 Encoding flow chart of the binary grating sampled double-phase hologram[25]

该方法实现了有限尺寸全息图的双相位分量的最紧凑排布，是目前为止对全息图空间带宽积利用率最高的一种方案。棋盘格采样的方法保证了从物体到全息图的运算过程中采样点数始终一致，极大地降低了运算的复杂性，提升了运算效率，是保证双相位全息图能够运用于实时全息显示的关键性一步，成为目前最广为使用的编码方法。但由于该方法中运用了互补采样，由双相位恢复的复振幅受相邻像素近似的影响，局部重建精度略低于巨像素方法。

2.4 双相位全息图的错位噪声

对双相位全息图重建质量造成影响的主要因素，在于每个复振幅调制单元内的双相位分量存在空间错位，无法完全相干叠加[20]。不论在单像素编码方法还是巨像素编码方法中，像素错位带来的噪声虽得到了抑制，但仍无法完全消除。错位的双相位分量在傅里叶变换后可具有固定的线性相位因子，因此对于填充因子为1的空间光调制器，重建的双相位全息图在频域可分解成信号项与噪声项两项加和的形式[23,26]：

H(u,v)=HS(u,v)+HN(u,v)，

(10)

其中HS(u,v) 为信号项：

(11)

HN(u,v) 为噪声项：

(12)

ES(u,v) 与EN(u,v) 为两项在频域的外包络函数：

学生由被动变主动。工科的理论课程多数以教师的讲解为主，学生作为知识的接受方一直处于被动的位置，如果教师讲授时理论推导和数学公式过多，而又没有相应的实践环节运用于检验，往往导致学生注意力不集中，学生仅仅记住了结论，学习效果不理想。针对这一现象，我们通过机械创新设计大赛，助推学生变被动接受为主动探索，迫使学生认真复习所学知识，起到举一反三、触类旁通作用，从而提高学生的实践运用与动手能力。

ES(u,v)=4αβsinc(αu)sinc(βv)×
cos(παu)cos(πβv)，

(13)

EN(u,v)=4αβsinc(αu)sinc(βv)×
sin(παu)sin(πβv)，

(14)

由此可得出，信号项的外包络函数将信号项限制在近轴低频区域，噪声项的外包络函数将噪声分散在信号的四周(图5)。

(a)信号项包络函数(a) Signal envelope function

由于噪声项分布在信号项四周，双相位全息图重建时需依靠空间滤波，遮挡大部分噪声项。但由于包络函数分布特性，空间滤波也无法完全消除全部位移噪声。且由于空间滤波消除了全息图频谱中的大多高频成分，双相位全息图空间带宽积因此受限，图像细节与空间分辨率较复振幅场重建受损。韩国KAIST大学Kim等人通过权重因子调整噪声项强度[27]，从而抑制错位噪声，扩大空间带宽积。清华大学与剑桥大学提出了带宽受限的双相位全息图[26，28]，通过双相位全息图信号项与噪声项包络函数定义带宽限制函数，提升双相位全息图的光学重建的空间带宽积与空间分辨率。并提出双相位全息图的时分复用方法，降低错位噪声对重建结果的影响。

2.5 双相位全息图应用于全息显示

双相位全息图由于其运算效率高、具备振幅与相位带宽、重建质量高，在全息显示上具有广泛深入的应用。如图6所示，基于双相位复振幅全息显示系统包含复振幅重建与物光波重建两部分。经过扩束准直的均匀强度平面波经分束器入射到相位型空间光调制器，经空间光调制器调制后的波前空间滤波，在4-f系统后焦面得到全息图的复振幅分布。复振幅波前在自由空间中传播一段距离，即可重建物光波波前。

图6 双相位全息图光学重建系统Fig.6 Optical setup for the reconstruction of double-phase hologram

双相位全息显示在光学重建上面临部分与相位型全息图重建相似的挑战。为消除空间光调制器反射光直流量，东南大学的Qi和Chang等人先后在双相位的空间滤波部分引入闪耀光栅分离零级光，进一步提升重建质量[29-30]，并在物体上添加二次球面相位简化显示系统，实现单透镜或无透镜双相位全息显示[31-32]。

双相位全息图由于其无需迭代，具有较高的计算效率。因为在三维全息显示，尤其实时显示方面，具备显著优势。2013年，北京理工大学的Li等人率先使用双相位全息图实现多层动态全息显示(图7)[33]。但由于双相位的带宽限制，在计算时无法使用随机相位，因此在基于双相位的多层的全息显示中，具有较为严重的层间串扰问题。为解决该问题，Li等人运用随机相位与迭代算法，实现连续三维物体的分层运算与双相位彩色重建(图8)[34]。

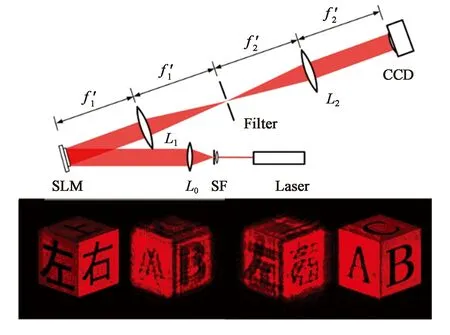
图7 双相位多层动态全息显示[33]Fig. 7 Dynamic multi-plane holographic display based on double-phase holograms[33]

图8 双相位彩色三维全息显示[34]Fig.8 Color three-dimensional holographic display based on double-phase holograms[34]

2017年，剑桥大学微软研究院的Maimone等人，基于双相位全息图原理提出大视场的全息虚拟现实与增强现实技术，开发出可变焦的大视场彩色近眼显示样机[35]。运用点源法与双相位编码实现复振幅全息波前的计算，使用GPU并行运算加速实现动态交互场景的实时运算与显示，并采用全息光学元件实现紧凑近眼显示系统的设计与搭建。图9为近眼显示系统与真三维重建结果。

(a)双相位近眼显示系统(a) Near-eye display system

3 相位干涉复振幅全息

依据双相位分解的原理可以得出，两个具有相同振幅的相位场严格相干叠加可恢复出原复振幅场。由此演变出复振幅全息图的另一种形式：相位干涉，即通过同一空间光调制器的不同分区或不同空间光调制器，使具有相同振幅不同相位的调制波前发生干涉，恢复复振幅波前。

3.1 单空间光调制器的相位干涉

使用单空间光调制器不同分区进行干涉的代表性工作，包括2012年韩国三星先进技术研究院[36],使用二元光栅耦合双相位分量，重建出二维复振幅全息图(图10)。为增强相位耦合，将4-f系统中的球面透镜替换为柱面透镜，达到了信噪声比为90%以上的重建效果。

(a)分区全息图(a) Divisional hologram

另一代表性工作为2012年德国SeeReal公司提出的复振幅实时显示系统(图11)，使空间光调制器相邻像素调制的光场经过结构半波片与双折射板进行空间上的光学组合，实现了多层场景的实时显示。定制的像素化光学元件，经过预先校准，保证重建中像素级干涉的实现[37]。

(a)多层光学重建(a) Multi-plane optical reconstruction

使用单空间光调制器的相位干涉复振幅全息需要在光学重建中实现空间光调制器自干涉，多依赖光路设计与特定元器件设计。其重建结果具有较高的理论精度，实际光学重建的过程中面临元件对准与光能利用率优化等挑战，还存在较大的发展空间。

3.2 空间光调制器组合的相位干涉

使用空间光调制器组合的相位干涉复振幅全息系统大多以泰曼格林干涉仪为雏形设计与搭建[38-39]。如图12，将干涉仪的反射镜替换为空间光调制器，两干涉臂内的入射平面波分别经不同空间光调制器调制为双相位分量。由此，两空间光调制器上载的相位分布在干涉光合束后相干叠加，在指定深度重建出全息图平面的复振幅场。

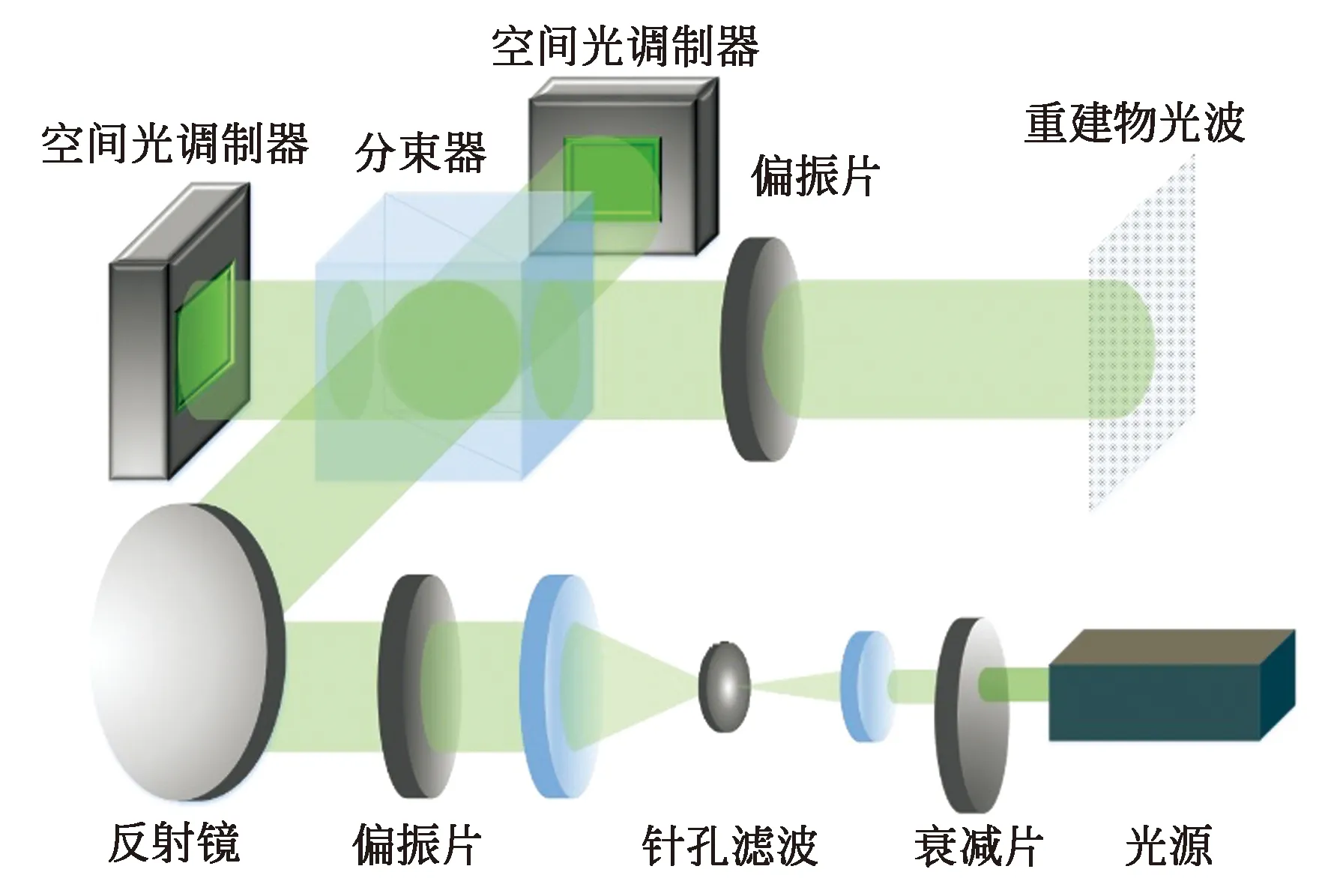
图12 相位干涉的复振幅全息重建系统Fig. 12 Complex holographic reconstruction based on phase interferometry

由于相位干涉的复振幅全息系统由干涉仪演变而来，因此它对环境的敏感度较高，重建要求两干涉臂的臂长严格相等[40]，细微的臂长波动都会对重建结果带来较大的影响。此外，相位干涉的复振幅重建要求两空间光调制器的出射光实现像素级的对准。受重建系统的苛刻条件影响，相位干涉的重建结果较难实现质量突破。

2016年Kreis基于泰曼格林干涉仪结构搭建相位干涉复振幅全息系统[41]。提出使用矩形单元格图案校准双空间光调制器的姿态，实现像素单元级别上的对准，并重建三维复振幅全息图(图13)。

(a)光学重建系统(a) Optical reconstructing system

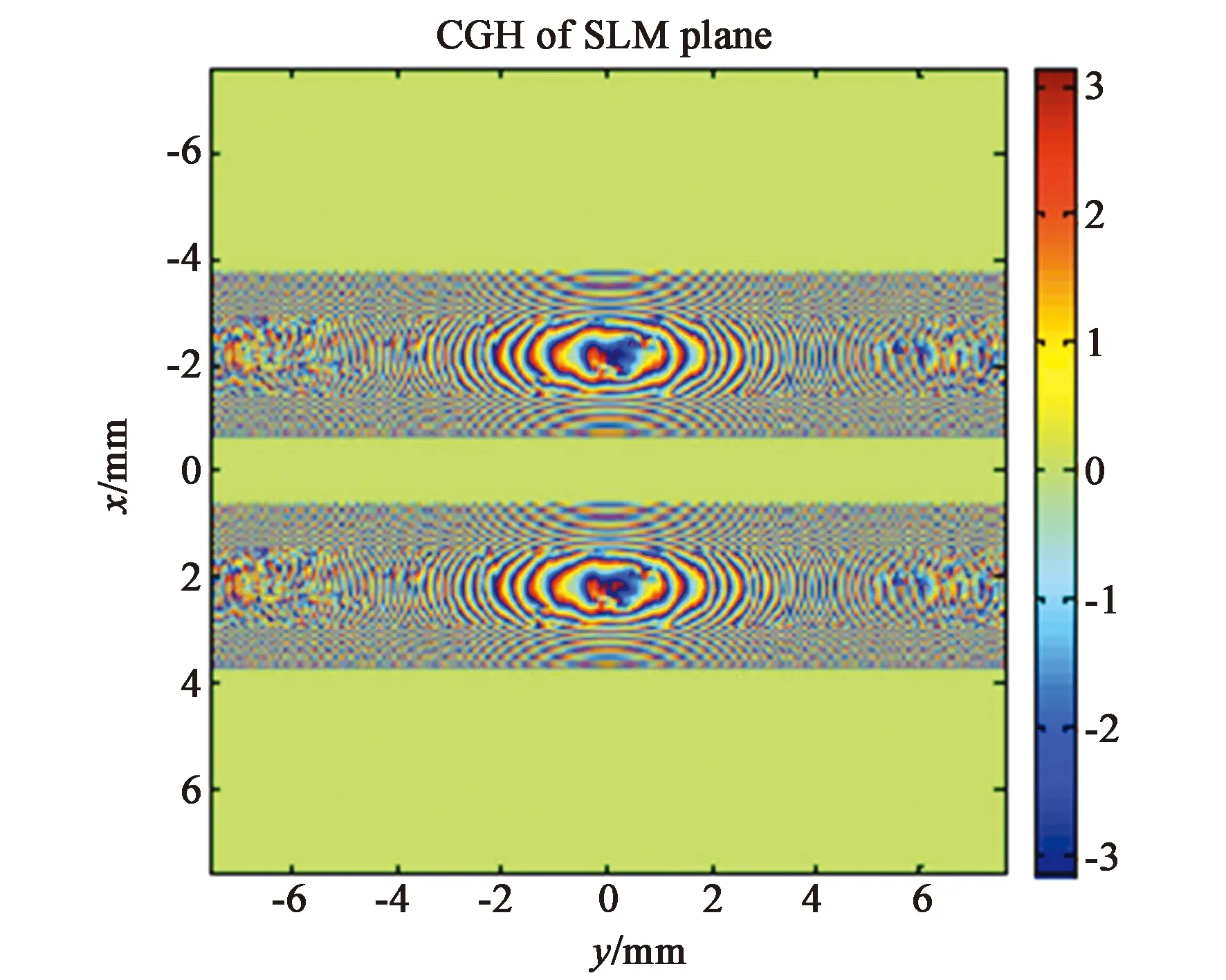
2021年，斯坦福大学与英伟达公司提出了基于硬件反馈循环的相位干涉复振幅全息系统。通过探测重建光场强度带入优化算法，通过迭代循环矫正空间光调制器上的相位分布，重建出具有高精度的复振幅全息图(图14)[42]。将该方法计算循环引入相位干涉，提供了一种实现相位干涉的新思路，极大地提升双相位分量的对准精度，使复振幅全息的重建质量产生跨越式提升。

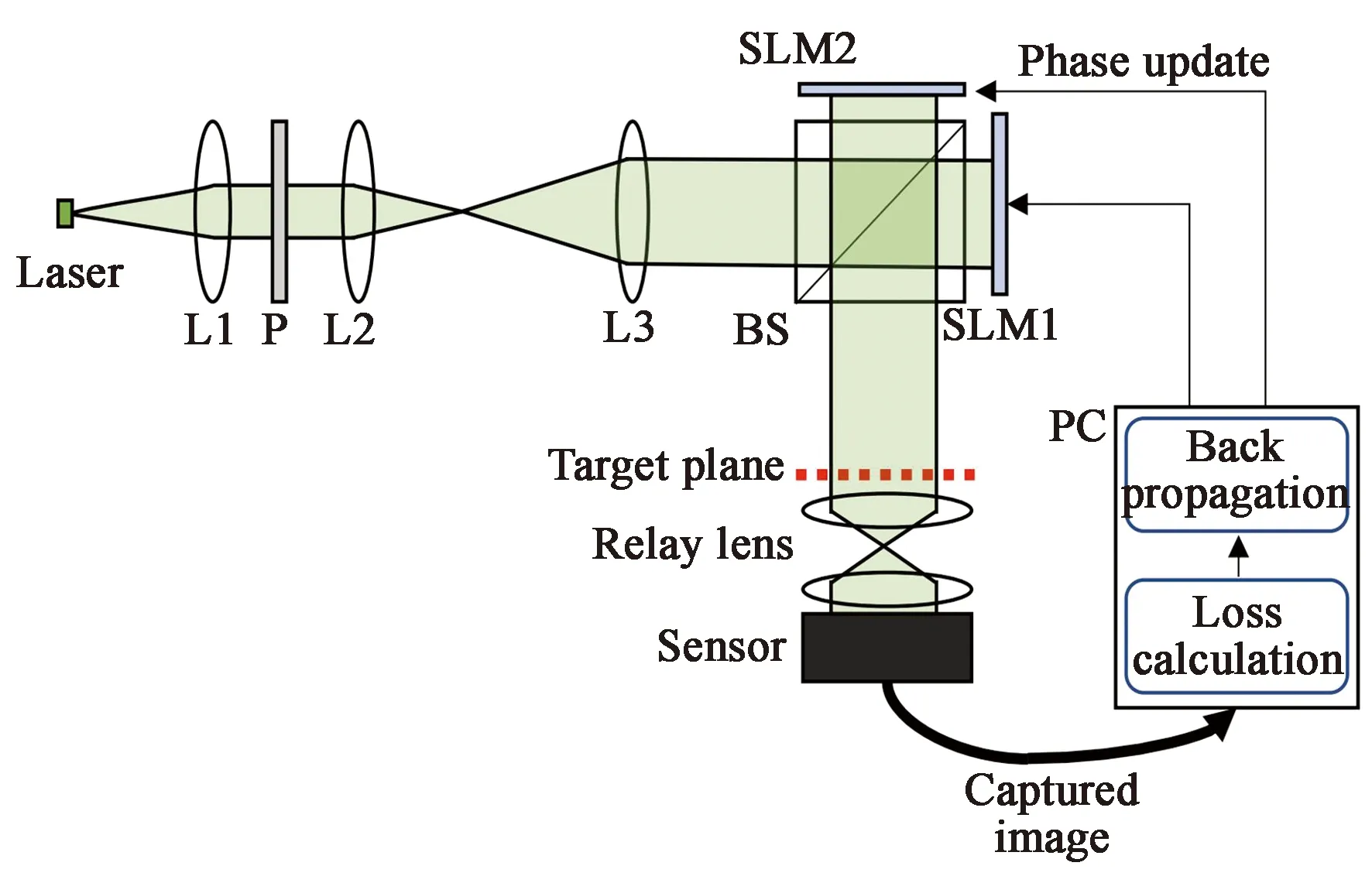
(a)硬件循环相位干涉系统(a)Camera-in-the-loop phase interferometric system

4 其他复振幅调制方案

随着全息显示的快速发展致使其对复振幅编码技术的需求与日俱增，也产生了其他复振幅调制的方案。

从相位型空间光调制器恢复复振幅场的角度出发，2014年Shibukawa等人通过在复振幅场频域添加数值随机相位掩膜版编码复振幅光场，成功恢复出编码光场的振幅与相位[43]。2019年，Shimobaba等人提出误差扩散与双相位组合的方式编码复振幅光场[44]，实现了无需空间滤波的直接衍射重建。

从振幅型空间光调制器恢复复振幅场的角度出发，2011年Liu等人提出了振幅型空间光调制器分区耦合的方案[45]，通过位移调控相移并在重建傅里叶平面内使用光栅耦合，重建出复振幅场。2021年，Jiao等人运用数字微镜器件冗余的编码自由度调制输入场的相位[46]，实现振幅型器件的复振幅重建。

此外，也可以通过组合空间光调制器对输入光波的振幅与相位依次级联调控，如1996年Neto等人使用一个振幅型空间光调制器与一个相位型空间光调制器依次调控振幅与相位[47]，建立不同振幅与相位输入值对应的复振幅查找表(Look Up Table, LUT)。2011年 Makowski等人使用两个相位型液晶空间光调制器组合调控(图15)[48]。调整入射与出射第一个空间光调制器的偏振态从而实现振幅调控，再入射到第二个空间光调制器实现相位调控。

(a)光学重建(a) Optical reconstruction

以超颖表面为代表的新型显示材料与显示元件迅速发展，为计算全息的波前调控与波前编码提供了新角度与新手段[49-50]。随着显示器件的革新，未来复振幅全息方案将日趋多样化，并最终向振幅与相位独立自由调控的目标迈进。

5 总结与展望

本文介绍了以双相位原理为主体的复振幅全息技术的进展，包括双相位全息图、相位干涉的复振幅全息及其他复振幅全息方案，分析不同复振幅调控方案的优势与挑战，并得出以下结论：

(1)复振幅调控是一个长久以来备受关注的领域，能够同时独立地调控光场的振幅与相位是人们对光场调控与操纵的重要目标。全息由于其通过复振幅波前记录与恢复理想物光波的特性，对编码、记录、显示的器件提出了处理与调控复振幅光场的需求，因此复振幅全息显示是全息显示的终极发展方向。

(2)近年来复振幅全息在算法、器件与系统层面均取得了跨越式的发展，以双相位为主的复振幅运算与编码方法兼备了高运算效率与高重建精度，有望实现高分辨率和大视场的真三维实时全息显示。以空间光调制器为代表的数字显示器件在向更多像素数目、更小像素尺寸与更高刷新速率快速发展，为复振幅显示技术的突破创造了条件。同时，超颖表面等新型光学元器件的发展，为复振幅调控器件创造了更多可能性。计算机技术的高速发展使得相对传统的相位干涉方法能够从光学上实现复振幅全息显示，克服了干涉系统应用于显示领域时存在的定位精度严格和稳定性受限等不足。

(3)复振幅全息对现有全息技术的算法、器件与系统也提出了更高的要求。复振幅全息在扩展空间带宽积的同时也极大地增加了计算全息的运算数据量，对复振幅光场的调控要求器件具备独立调控多阶振幅与相位的能力，算法与器件噪声的大幅降低致使复振幅全息对光路噪声的可控性有了极高的要求。

(4)未来复振幅全息的调制手段将日趋多样化，针对不同的显示应用场景，采用不同的调制和显示器件、设计适配的显示系统与运算算法将是未来复振幅全息显示的发展方向。