两栖机器人海流发电涡轮结构优化设计*

石欣平，肖 莉，张尚盈,2※

（1.武汉工程大学机电工程学院，武汉 430205；2.武汉誉琼科技有限公司，武汉 430205）

0 引言

水陆两栖机器人能够代替人类完成陆地及水下等复杂环境中的侦查、勘探等任务，需要具备灵活、小巧的特点以及优越的通讯和续航能力[1]。两栖机器人的续航大多采用自身携带能源的方式，其中包括一次电池、二次电池、燃料电池及热机等[2]。这种续航方式往往会增加机器人的体积与负重，降低机器人的运动敏捷性，且这种方式可利用的能源十分有限，往往无法实现在较深水域的长时间勘探工作。某大学研制的AQUA系列两栖六足机器人，其自身携带的镍氧电池仅可以维持不间断操作2 h[3－4]；Eric Stackpole与David Lang推出的用于水下摄影的机器人Open ROVs，其采用的锂电池可以为自身续航3 h。未来，两栖机器人的续航能力将是影响其综合性能的关键因素。国内某研究所通过采用多孔介质材料作为耐压壳体的表层，降低了航行阻力，使自主水下机器人在外形和电池容量不变的情况下提高了续航能力[5]。

利用海洋自然环境条件[6]，针对可下潜1 000 m海洋中长时间工作的水陆两栖机器人，本文设计了一种可以为机器人续航的海流能发电涡轮结构。选取了某经典系列翼型中的几种不同翼型进行了动力特性的分析，分析了叶片数量与轮式结构对海流发电涡轮输出功率的影响。

1 涡轮翼型选取

1.1 涡轮翼型特征

为了得到更高输出功率的海流能发电涡轮，需选取升阻比较大的翼型进行涡轮建模[7－8]。NACA 6系列翼型是某系列经典翼型，是具有较高的最大升力系数的一类层流翼型，这类翼型在一定升力系数范围内具有低阻力特性，在非设计工况下也具备较好的性能[9]。在NACA 6系列翼型中，63、64、65三种翼型具有不同的厚度分布，其厚度分布使0升力下的最小压力位置分别在弦长的0.3、0.4、0.5处，翼型数据显示，在低雷诺数流动中，63系列翼型具有更加优秀的动力特性。

故选取相对厚度相同的NACA 63系列中的63－215、63－415、63－615翼型进行特征比较，如图1所示。这3种翼型的设计升力系数分别为0.2、0.4、0.6，不同的设计升力系数导致翼型相对弯度也有所不同，设计升力系数越大的翼型，其相对弯度越大。

图1 不同设计升力系数的翼型几何特征

1.2 涡轮翼型动力特性分析

将翼型坐标导入ICEM进行计算域及网格的划分，如图2所示。C为翼型弦长100 mm，计算域边界AFE、DE的边界条件为速度入口，流速为1.5 m/s，边界AB、BD的边界条件为压力出口，翼型airfoil的边界条件为壁面，生成网格数量为61 686，且网格经过独立性检验，质量良好。

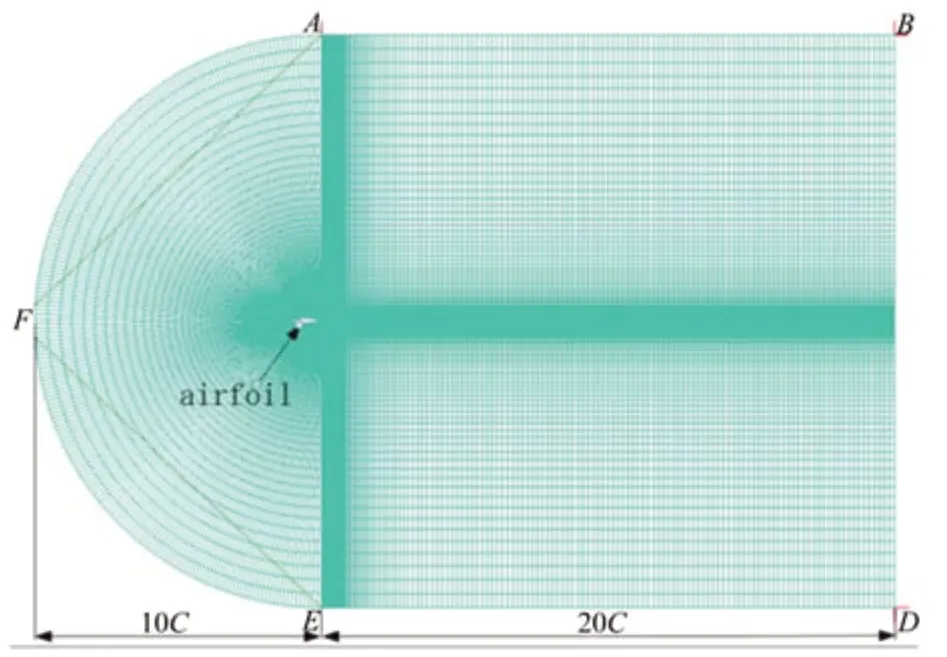
图2 计算域网格

SST k－ω模型具备k－ω模型近壁区的计算优点以及标准k－ε模型远场计算的优点，同时，模型中的湍流黏度考虑了湍流剪切应力的传递过程，更适用于翼型的计算。故本文采用SST k－ω模型进行数值模拟，得到的各翼型不同攻角下的升阻力系数比，如图3所示。由图可以看出NACA 63－615翼型具备较高的升阻比，当攻角α＜6.5°时，翼型升阻比随着攻角的增大而稳步增大；当攻角α＞6.5°时，翼型升阻比随着攻角的增大而减小，因此，该翼型的最佳攻角为6.5°。

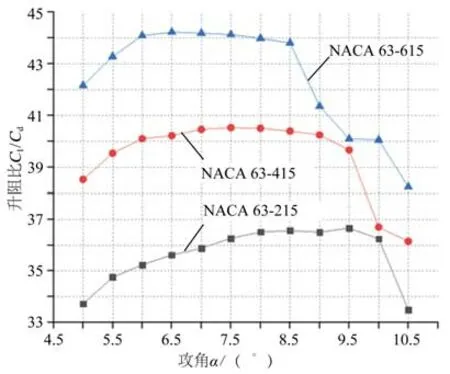
图3 翼型升阻比

2 涡轮结构的优化设计与建模

2.1 叶片的优化设计与建模

根据Wilson优化设计理论[10－11]，现将叶片分为多个微元，并引入普朗特叶尖损失修正参数F，可表示为：

其中，f为中间变量，可表示为：

式中：B为叶片数量；R为叶轮半径，取0.12 m；r为微元处半径；φ为入流角。

引入叶片轴向诱导因子a；周向诱导因子b，两变量关系为：

且有功率系数CP：

式中：λ0为叶轮叶尖速比；λi为半径r处叶素的叶尖速比。

以式（4）为目标函数，式（1）～（3）为约束方程通过最优化函数fmincon求解各叶素弦长C及扭角β并进行修正，其设计流程如图4所示。

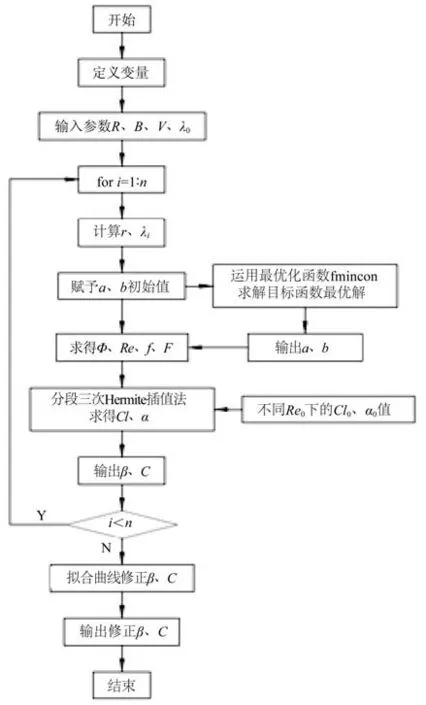
图4 叶片设计流程

以原始翼型动力中心（弦线上距离翼型前缘1/3处）为原点进行坐标变换，具体变换公式如下：

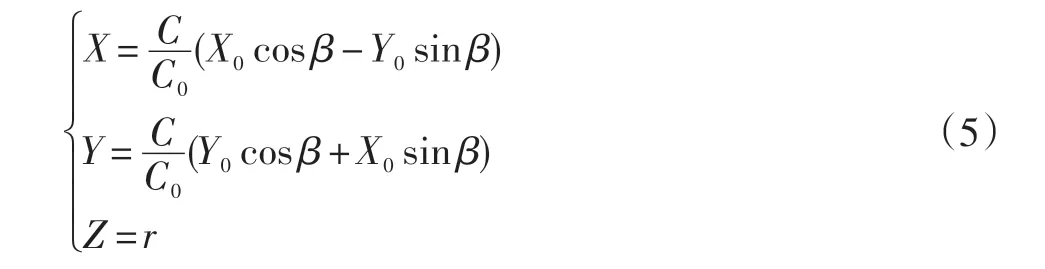
式中：C0、X0、Y0为原始翼型的弦长与坐标参数。

根据变换后的翼型坐标参数可得到各叶素与叶片的模型如图5所示。

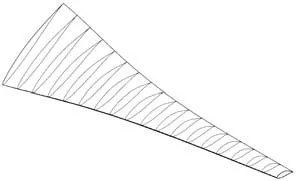
图5 叶素与叶片模型

2.2 涡轮轮周的优化设计与建模

为了减轻外缘轮周的重量并降低卡门涡街效应的影响，将轮周的截面形状进行优化，如图6所示，将竖直端面用1/4椭圆代替，该椭圆的长半轴为15 mm、短半轴为10 mm。

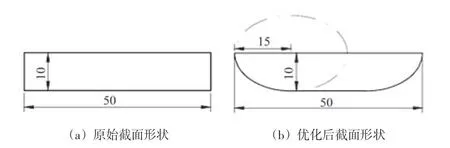
图6 轮周截面形状

根据参考文献[12]，3～5叶片中低速叶轮的叶尖速比一般为2～4，这里取叶尖速比为3，建立3～5叶片的海流发电涡轮模型如图7所示。

图7 海流发电涡轮模型

3 海流发电涡轮动力特性分析

采用MRF（多重参考）模型进行数值模拟，将计算域划分为外部静止域与内部旋转域两个区域[13]，具体划分情况及边界命名情况如图8所示，其中D为海流发电涡轮直径260 mm。对内外两个流体域均进行非结构网格的划分，生成100万网格，网格质量良好且经过独立性检验。

图8 计算域划分及边界命名

设置静止域入口处inlet边界条件为速度入口，流速为1.5 m/s，出口处outlet边界条件为压力出口，外部wall＿out边界条件为壁面，静止域与旋转域的交界面为interface，旋转域沿Y轴方向逆时针旋转，转速为358 r/min，海流发电涡轮外表面wall＿in边界条件为壁面，其运动状态与旋转域保持相对静止。采用在旋转流计算中，计算结果更符合真实情况的Realizable k－ε模型进行计算，结果如表1所示，四叶片海流发电涡轮具有最大输出功率。

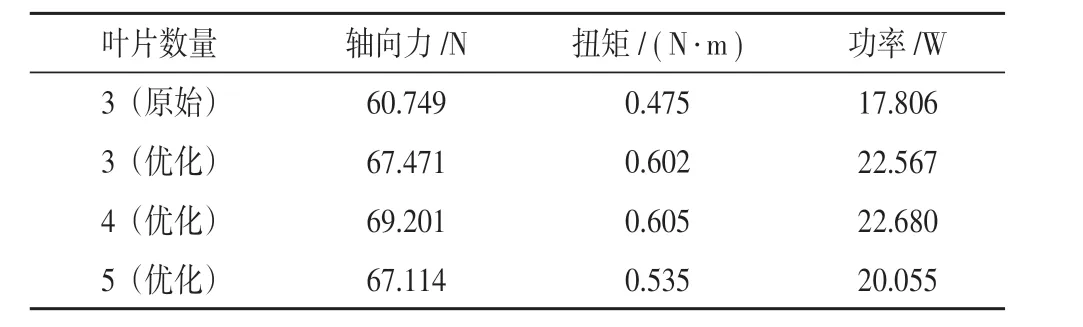
表1 数值模拟结果

功率公式：

式中：Cp为四叶片海流发电涡轮的捕能系数，代表该结构捕获能量效率的高低；ρ为海水密度，取1 025 kg/m3；A为叶片扫掠面积；v为海流速度，取1.5 m/s。

经计算可得捕能系数Cp＝0.290，接近横轴水轮机的平均捕能系数0.3，该结果表明，海流发电涡轮结构的捕能效率良好。

图9所示为海流发电涡轮的速度云图以及叶片表面所受压强的分布情况，迎流面靠近叶尖处有压强最大值，背流面靠近叶尖处有压强最小值，这表明叶片叶尖处的压差值最大即海流发电涡轮的动力主要来源于叶尖。此外，湍流主要分布在涡轮背流面的叶根及轮周边缘处，通过图9（a）与（b）的对比，可以看出优化后的外缘轮周处湍流明显减少，海流发电涡轮的输出功率得到了明显提高。

图9 速度云图与压强分布

4 结束语

本文针对水陆两栖机器人的水下续航问题，将两栖机器人水下发电结构与陆地行进结构合二为一进行了优化设计，提供了一种新的解决方案。通过Wilson优化设计理论，求得了各叶素弦长与扭角的最优解，对各叶素弦长与扭角曲线的拟合与修正，以及对原始翼型坐标的变换，得到了动力特性优良的叶素单元及叶片模型，对轮周截面形状的优化，大大降低了卡门涡街效应的影响。仿真结果表明，该海流发电涡轮结构具有较高的输出功率，捕能效率良好，能够提高水陆两栖机器人在水下工作时的续航能力。