特种汽车轮边减速系统齿轮传动力学特性分析
2021-07-14武之剑朱学斌李浩鹏
李 阳,武之剑,朱学斌,李浩鹏
(泰安航天特种车有限公司,山东泰安 271000)
0 引言
特种汽车一般采用主减速器和轮边减速系统两级减速来适应低速、高扭等复杂工作环境下的使用要求。轮边减速系统作为簧下组件,其受力环境更为复杂。
齿轮系统的模型根据研究内容不同有多种分类,如动载系数模型、齿轮副扭转振动模型、传动系统模型和完整齿轮系统模型[1-4]。扭转振动模型因其更简易的计算方法,常被用于齿轮的传动轴较大和轴承对齿轮支撑较大的齿轮进行建模。本文以汽车轮边减速系统齿轮为研究对象,建立单级齿轮动力学模型,基于Runge-Kutta法编程求解,分析单级齿轮的传动力学特性,为复杂环境下特种汽车轮边减速系统性能设计提供理论基础。
1 建立动力学模型
将图1所示的轮边减速系统齿轮副简化为图2所示的受力简图。其中r1、r2分别为主、从齿轮的基圆半径;I1、I2分别为主、从动齿轮的转动惯量;θ1、θ2分别为主、从动齿轮的扭转角位移;T1、T2分别为作用在主、从动齿轮上的扭矩;k(τ)为时变啮合刚度;Cg为齿轮副的啮合阻尼;e(τ)为轮齿副的啮合综合误差。

根据牛顿第二定律可以得到系统的运动微分方程组:

定义主、从动齿轮沿着啮合线上位移的分别为x1、x2,则:

两个啮合齿轮的等效质量表示成mi=Ii/ri2。联合式(1)、(2),进一步简化可得:

式中:mi为齿轮的当量质量,i=1为主动齿轮,i=2为从动齿轮;Fi=Ti/ri为齿轮i上作用的啮合力;κ(τ)为齿轮啮合过程中的时变啮合刚度;f(x)为齿侧间隙函数[5]。
将齿轮系统的传动误差设为s,用相对位移表示为:

联合式(1)、(4)简化可得:

式中:齿轮副等效质量m=m1m2/(m1+m2);F(τ )为系统受到的激励。
激励函数如下:

齿轮的时变啮合刚度k(τ)是随时间变化的周期函数,表示为傅里叶级数[6],取一阶谐波分量,则时变啮合刚度为:

式中:k0为齿轮啮合过程中的平均啮合刚度;ka为齿轮系统时变啮合刚度波动幅值;φh为初相位。
齿轮刚度与综合啮合误差初始相位之间的关系为:φh=φe+π,将式(6)、(7)代入式(5),得到系统微分方程:

选取如下无量纲参数:

则系统微分方程的无量纲化形式为:

x1、x2分别表示齿轮过程中传动误差[7]的无量纲位移和速度,可得齿轮传动系统的状态方程:
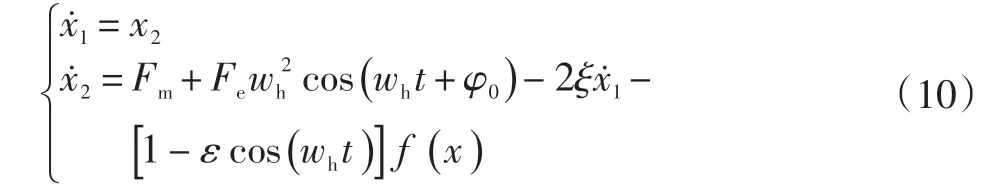
2 基于Runge-Kutta法的动力学模型分析
基于Runge-Kutta法将齿轮系统的动力学状态方程编程,在求解过程中运用ode-45函数将齿轮系统运动微分方程中的高阶方程转化为低阶方程。令Fm=0.1,Fa=0.2,ε=0.1,wn=1,同时取初始条件x1=0、x2=0。通过改变齿侧间隙的值,得到系统在不同齿侧间隙下的位移、速度图像的分岔图,通过分析比较,获得齿轮在不同间隙下的动力学特性。
图3所示为D=1时系统随阻尼比ξ的值变化的分叉图,从位移图中可以看出随着阻尼比的增大,齿轮系统的运动状态也会发生变化:当阻尼比ξ<0.056时,系统运动状态比较混乱,产生混沌运动,运动极不平稳,振动、冲击比较大;0.056<ξ<0.12时,系统混沌状态减弱,振动、冲击减小,系统相比较ξ<0.056的运动较平稳;ξ=0.12时产生分岔,系统基本稳定;ξ=0.32时系统集中为1个岔,系统开始平稳运行。
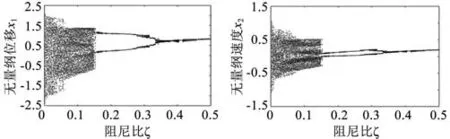
图3 齿侧间隙D=1速度—阻尼比图像
图4 所示为D=0.8时系统随阻尼比ξ的值变化的分岔图。随着阻尼比的增大,齿轮系统的运动状态发生变化:当阻尼比ξ=0.04时,系统运动状态比较混乱,产生混沌运动,运动极不平稳,振动、冲击比较大;0.04<ξ<0.15时,系统混沌状态减弱,振动、冲击减小;ξ=0.15时产生分岔;ξ=0.33时系统集中为1个岔,系统开始平稳运行。
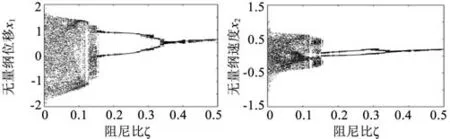
图4 齿侧间隙D=0.8时速度—阻尼比图像
图5 所示为D=0.5时系统随阻尼比ξ的值变化的分岔图,随着阻尼比的增大,齿轮系统的运动状态发生变化:当阻尼比ξ<0.035时,系统运动状态比较混乱,产生混沌运动,运动极不平稳,振动、冲击比较大;0.035<ξ<0.18时,系统混沌状态减弱,振动、冲击减小;当ξ=0.34时系统产生2个分岔,系统基本稳定;ξ=0.39时系统集中为1个岔,系统开始平稳运行。
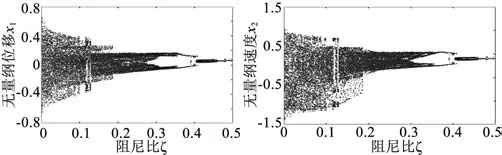
图5 齿侧间隙D=0.5时速度—阻尼比图像
图6所示为D=0.2时系统随阻尼比ξ的值变化的分岔图,随着阻尼比的增大,齿轮系统的运动状态发生变化:当阻尼比ξ<0.08时,系统运动状态比较混乱,产生混沌运动,运动极不平稳,振动、冲击比较大;0.08<ξ<0.13时,系统混沌状态减弱,振动、冲击减小;ξ=0.15时系统集中为1个岔,系统开始平稳运行。

图6 齿侧间隙D=0.2时速度—阻尼比图像
再利用齿侧间隙值为定值时,通过改变阻尼比的值来分析系统的稳定性,当齿侧间隙值为1时,改变阻尼比ξ的值得到系统的运动相图如图7所示。

图7 不同阻尼比下齿轮运动相图
图中,当齿侧间隙为定值时,齿轮系统随着阻尼比ξ的不断增大,齿轮系统的运动状态也在不断的改变,阻尼比很小时,系统处于混沌状态,系统的冲击、振动极大,系统处于极不稳定状态。随着阻尼比的增大,系统的混沌状态逐渐减弱,振动、冲击较小,系统逐渐趋于平稳;当系统的阻尼比增大到一定值时,系统的混沌状态基本消失,齿轮系统的运动和冲击都较小,系统趋于稳定的运动状态。
综上所述,当齿轮的齿侧间隙为定值时,齿轮系统在刚进入啮合时不稳定,在某一个瞬间会达到非常不稳定的状态,随着时间的推移在齿轮系统会在某一时刻处于稳定运转的状态。当齿轮系统的齿侧间隙不断增大时,齿轮系统的冲击也会随着齿侧间隙的增大而变大,系统的混沌状态也就越严重。
3 结束语
本文通过对特种汽车轮边减速系统齿轮传动力学特性分析得出以下结论。
(1)随齿轮系统的齿侧间隙不断增大,齿轮系统的冲击变大,系统的混沌状态也就越严重;
(2)当齿轮的齿侧间隙为定值时,齿轮系统在刚进入啮合时不稳定,在某一个瞬间会达到非常不稳定的状态,随着时间的推移在齿轮系统会在某一时刻处于稳定运转的状态;
(3)随阻尼比的增大,系统逐渐趋于平稳,系统的混沌状态基本消失,齿轮系统的运动状态趋于稳定。
