并联机构支链误差耦合分析

赵俊杰，周晓静，雷俊松

（1.河北工业职业技术学院宣钢分院，河北张家口 075100；2.珠海格力电器股份有限公司，广东珠海 519000）

0 引言

并联机构已经广泛应用于实际生产中，如数控加工、精密装配、航天等领域。精度的高低是评价机构性能的重要指标之一[1]，故对并联机构精度研究十分必要。张国庆[2]利用矢量链法和数值法对六自由度机器人进行了标定和分析；樊锐[3]对6PUS并联机构运用最小二乘法进行了整机标定；张文昌[4]使用激光跟踪仪对Delta机构进行了运动学误差标定；黄田[5]利用矢量链法对一种含有平行四边形机构进行了误差分析，并对误差进行了灵敏度分析；汪劲松[6]利用D－H法对Stewart机构建立了误差模型，但是上述理论是通过不同的方式建立起机构定平台到机构末端点的单支链误差方程，并没有关于研究分析各个支链误差耦合之后末端点的精度问题，即没有研究并联机构各支链误差耦合。目前对于并联机构精度问题国内外主要学者侧重于使用不同的方法建立机构误差模型，同时使用不同算法进行误差参数辨识。本文以三自由度并联机构[7]为研究对象，将各个支链叠加后的误差分别加入到该机构正解解析法和数值法中，对比分析结果一致，说明该方法的有效性，进而使用该方法对Stewart机构进行分析。

1 三自由度并联机构误差耦合分析

1.1 误差模型

本文所研究的三自由度并联机构是由动平台、静平台以及连接动静平台的3条支链所组成的，具体如图1所示。3条支链互呈120°对称，每条支链是由支柱、滑块、平行四边形结构支链组成，安放在立柱上的滚珠丝杠通过电机带动，使得立柱上的滑块上下移动，滑块同时通过转动副连接平行四边形结构的一端的短杆，平行四边形结构另一端的短杆通过转动副连接到动平台上，3条支链相互作用，使动平台能够进行三自由度移动。

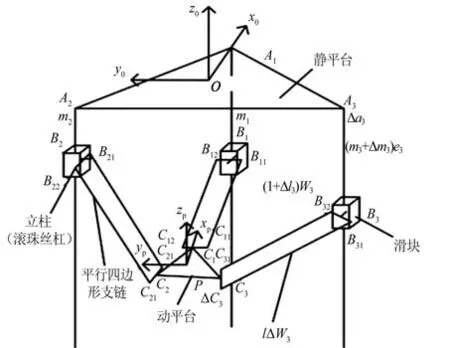
图1 三自由度并联机构坐标系

首先建立坐标系。静平台定参考坐标系{O}建立，xy平面为静平台上3个顶点理想位置所构成的平面，x轴指向A1，z轴方向垂直于xy平面并朝上，y轴满足右手定则，坐标系的原点O位于静平台中心。坐标系{Oi}建立，坐标系{Oi}和坐标系{O}原点完全重合，坐标系{O1}和坐标系{O}各轴方向一致，坐标系{O2}和{O3}分别绕坐标系{O}的z轴逆时针旋转2π/3和4π/3。顶点坐标系{Ai}建立，其坐标系的原点为静平台3个Ai顶点，坐标系{Ai}各个轴的方向和坐标系{Oi}各个轴的方向重合。顶点坐标系各个顶点的名义矢量和误差矢量分别为ai和Δai，坐标系{Ai}的姿态误差矢量为θAi。由点Ai至点Bi的名义值和误差值分别为mi和Δmi。滑块坐标系{Bi}建立，原点为铰链转动轴心Bi，坐标系{Bi}各个轴的方向和坐标系{Ai}各个轴的方向重合。点Bi坐标系名义矢量和误差矢量为bi和Δbi，坐标系{Bi}的姿态误差矢量为θBi。平行四边形结构端点铰链坐标系{Bij}建立，原点为铰链转动轴心Bij，其中y轴与两铰链中心线连线重合，箭头的方向由Bi指向Bij，z轴指向静平台，x轴满足右手定则，两铰链转动中心名义值及误差值分别为e和Δbij。动平台定参考系{P}建立，原点P位于动平台中心，xy平面平行于静平台，x轴指向C1，z轴垂直于动平台向上，y轴满足右手定则。坐标系{P1}和坐标系{P}重合，坐标系{P2}是绕坐标系{P}的z轴旋转2π/3而形成的，坐标系{P3}是绕坐标系{P}的z轴旋转4π/3而形成的。坐标系{P}相对于静平台定参考系{O}的误差矢量为θ。铰链坐标系{Ci}建立，原点为动平台铰链转动轴心Ci，坐标系{Ci}各个轴向方向和坐标系各个轴向{Pi}重合，点Ci坐标系名义矢量和误差矢量为ci和Δci，坐标系{Ci}的姿态误差矢量为θci。铰链坐标系{Cij}建立，原点为点Cij，其y轴与两铰链中心轴线连线重合，箭头方向是由转动副指向铰链，两铰链转动中心名义值及误差值分别为e和Δcij。连杆li的方向是由Bij指向Cij，平行四边形结构的长杆杆长的名义值和误差值分别为L和ΔLi，方向单位矢量的理论值和误差值分别为wi和Δwi。

在坐标系O－xyz下，根据矢量链法建立机构位姿闭环约束方程[5]。

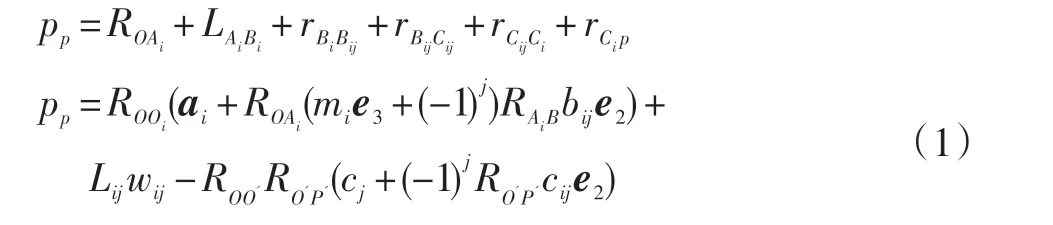
式中：i＝1，2，3；j＝1，2；e2＝[0，1，0]T；e3＝[0，0，1]T。

对式（1）进行1阶摄动得[6]：

式中：Δpp为点P的3×1阶位置误差，Ri为指静平台坐标系{O}相对于坐标系{Oi}的转换矩阵。

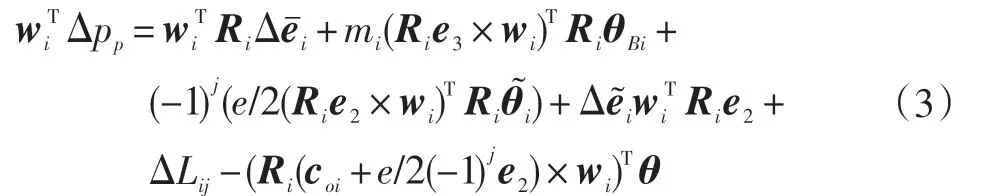
根据式（3）中j的不同取值，可知每条支链都有两个方程，将第i条支链的两个平行四边形的方程分别相减得式（4）：

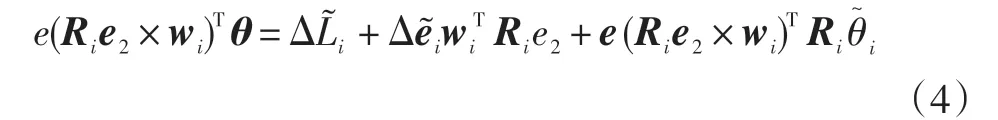
根据式（3）中j的不同取值，可知每条支链都有2个方程，将第i条支链的2个平行四边形的方程分别相加，并加式（4）中的θ代入得：

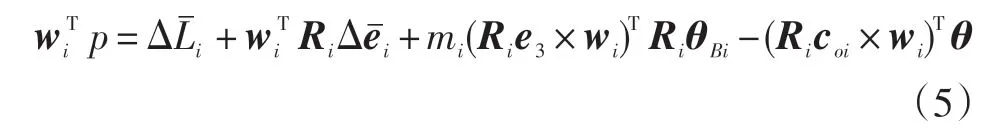
通过对式（5）分析得知，θBizRie3在（Rie3×wi）上投影为0，由此得出影响姿态的误差源个数总共为30个，分别是

1.2 并联机构正解

机构正解是指已知其驱动量的大小，通过计算求解得机构末端位置和姿态[2]。并联机构正解一般有2种方式：（1）解析法，即利用并联机构杆长和位置关系建立多元二次方程组；（2）数值法，利用数值迭代的方法逐步逼近机构的位置。解析法的特点是计算快、能够求出所有解，但缺点是因其是求多元二次方程组，求解的难度是随着未知数的个数增加，对于多自由度机构求解比较困难；数值法的特点是求解方法相对简单，但求解速度要比解析法慢。本文利用2种方法求解了三自由度并联机构。

（1）解析法

根据三自由度机构的位置关系可以建立一组三元二次方程组，如式（6）所示。

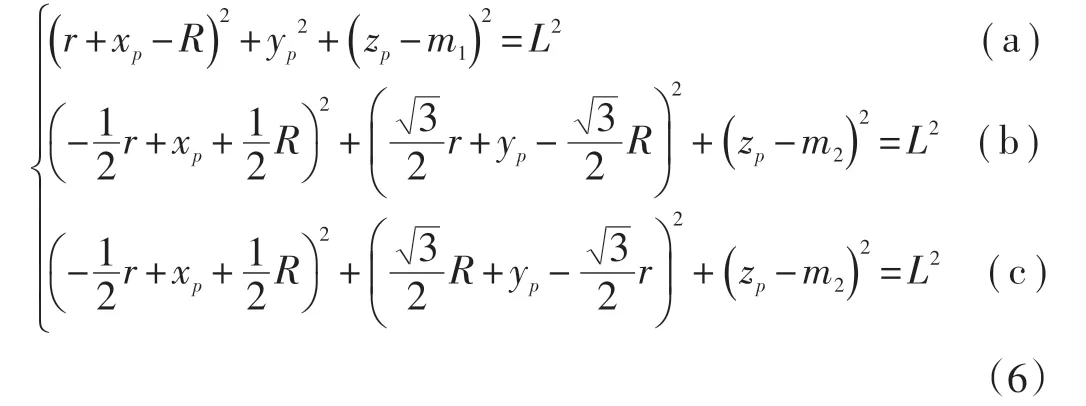
由式（6b）、（6c）得：

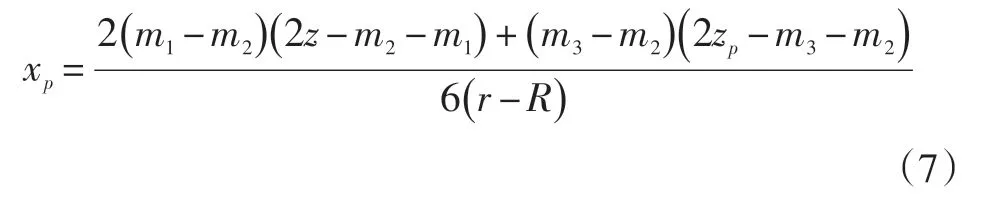
将xp代入式（6b）、（6c）得：

把xp和yp代入到式（6a）中得：

其中：

（2）数值法

正解步骤如下。首先给出一组位置坐标，并对其进行位置反解，将反解出的滑块位移和输入滑块位移进行相减，若相减之后的值达到设定的精度要求则记录该点位置；若没有达到，利用相减的差值和代入之前位置坐标的雅可比逆矩阵相乘，便得到一组修正位置，将得到修正位置和之前的位置坐标相加得到新的位置，对该位置继续求解滑块位移。数值法正解流程如图2所示。

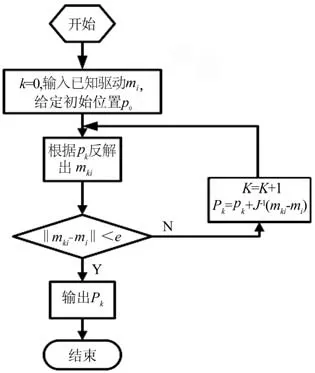
图2 并联机构正解流程

三自由度并联机构尺寸如下，定平台直径为1 500 mm，动平台直径为700 mm，平行四边形结构，长杆长度为750 mm，短杆长度为200 mm。在给定的工作空间z＝－600 mm，xy在圆r≤20 mm上选取72个点。利用Matlab对其进行2种正解方法验证，其中数值法精度设定为0.000 001 mm。计算结果如图3所示，其中横坐标代表测试点，纵坐标为根号下x、y、z 3个方向误差平方和，即从中可以知道，无论是解析法还是数值法，都能准确地得到机构的位置，还存在误差的原因是计算机计算精度所致。

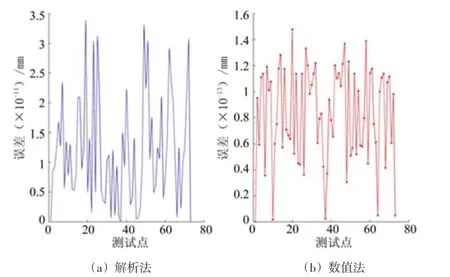
图3 三自由度并联机构正解误差

1.3 误差耦合分析

本文只探讨误差耦合对于机构精度的影响，误差的随机性不在此次研究范围内，所以将三自由度并联机构的各个误差值设定为定值[7]。具体值如表1所示。

表1 三自由度并联机构误差值 mm

将以上各个单链的误差（共30个）参数代入式（5）各条支链误差方程中，并进行全局坐标转换，此时可以得到3条支链在全局下的坐标误差，再将每条单链上的误差代入到三自由度正解的2种解法中。解析法误差耦合如图4所示，把各个单链累计后的误差带入该机构正解方程，即式（6）中，由于支链误差的存在改变了正解方程，将不含误差的驱动量代入方程中，可以得到此时该机构将各支链误差耦合之后末端位置的误差。数值法误差耦合如图5所示，将各条支链上的误差转换为各条支链上的驱动误差，最终将驱动误差通过数值法转换为末端的位置误差。继续使用正解中的72个点进行分析，其结果如图6～8所示，其分别代表了每条支链上不同方向的误差和经过耦合代入正解中的各个轴向的误差。通过观察，发现2种正解方法得出的耦合误差结果相同，相互印证了利用正解方法代入求出机构末端位置误差的有效性；其次，通过分析对比发现，并联机构耦合之后的误差小于各支链方向性的误差，即通过耦合后，各个方向上的误差对于动平台的误差影响会降低，这也可解释并联机构的精度要比串联机构精度高的原因。

图4 解析法流程

图5 数值法流程

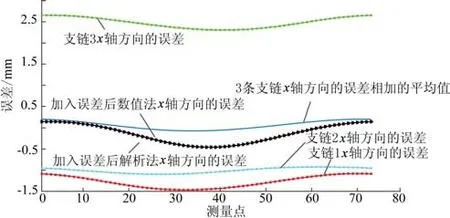
图6 三自由度并联机构x轴误差

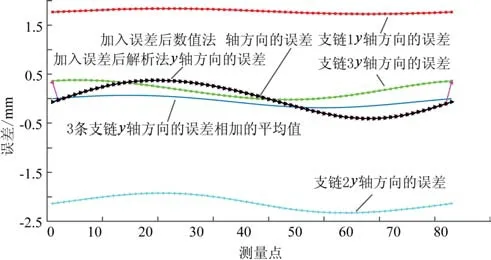
图7 三自由度并联机构y轴误差

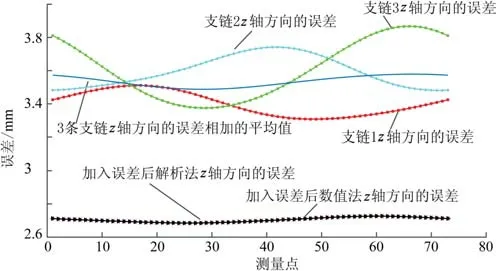
图8 三自由度并联机构z轴误差

通过分析可以得出如下结论：并联机构经过耦合后，机构的结构可以消除一部分误差；耦合的误差要比各个支链相加要小很多；耦合之后的误差大小和各个支链误差相加后并没有明显的联系。

2 Stewart机构误差分析

Stewart机构是并联机构中使用比较多且比较成熟的机构，在第1节中利用正解的2种算法已经证明了该方法的有效性，本节将误差加入到Stewart机构的正解中去，研究其误差耦合特性。首先对机构进行介绍，Stewart机构是由动平台、静平台以及连接动静平台的6条支链构成。按照铰链形式的不同，其可以被分为6－UPS、6－SPS或是6－UCU等。本文针对6－UPS机构进行研究，如图10所示。该机构静平台直径为540 mm，动平台直径为480 mm，最短杆长为500 mm，最长为900 mm。由于Stewart机构的位置正解是求一组六元二次方程组，求解较困难，采用数值法对其进行求解。在z＝610，x＝20 cosα，y＝20 sinα上选取72个点进行正解验证。其中误差杆长精度设定为0.000 001 mm。结果如图9所示，图中可以清晰地看出数值法对于求解Stewart机构的有效性。

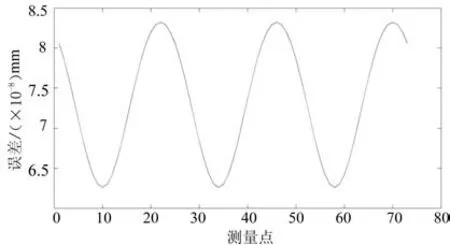
图9 Stewart机构正解平均误差图

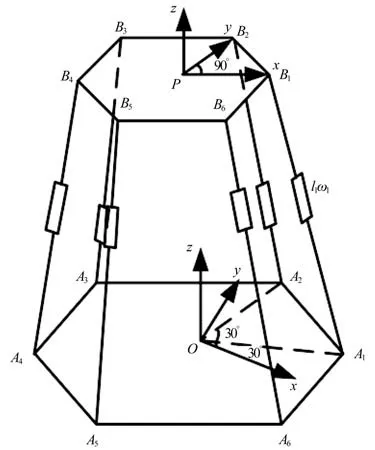
图10 Stewart并联机构坐标系

图10 所示为采用矢量法对其进行误差建模。首先在静平台建立根坐标系{O}，坐标系{O}原点位于静平台中心点，x轴和点A1呈30°夹角，z轴指向上方，通过右手定则便可以获得y轴的方向。建立坐标系{Oi}，其中xy平面不变，绕z轴旋转使x轴指向静平台上的各个铰点。规定各个铰点理想坐标为a，误差为Δa。各个理想杆长为l实际杆长为Δl。动平台坐标系{Op}建立，规定动xy平面和动平台平面重合z轴垂直于动平台指向上方，x轴和点b呈－30°夹角。建立坐标系{Ooi}，其中xy平面不变绕z轴旋转使x轴指向动平台上的各个铰点。在坐标系O－xyz下，根据矢量链法建立机构位姿闭环约束方程，如式（10）。

对式（10）进行1阶摄动得：

对式（11）进行分析，每条支链有7个误差分别是Δaix、Δaiy、Δaiz、Δli、Δbix、Δbiy、Δaiz，总共有6条支链，所以误差源总共为42个。

同三自由度并联机构一样，只分析误差耦合对于机构动平台的影响，所以误差的随机性不在此次考虑中。规定机构的误差如表2所示。

表2 Stewart并联机构误差值 mm

将表中的误差代入到Stewart机构的数值法正解中，即流程图求解杆长的方程中，继续使用正解中的72个点进行分析。结果如图11～14所示。

图11 Stewart机构x轴误差

从图11～14可以看出，不同的单链经过误差耦合之后，动平台端的误差都要比单链最大的误差小，同三自由度并联机构一起分析，可以得出如下结论：并联机构经过耦合后，机构的结构可以消除一部分的误差；耦合的误差要比各个支链相加要小很多；耦合之后的误差大小和各个支链误差相加后并没有明显的联系。

图12 Stewart机构y轴误差

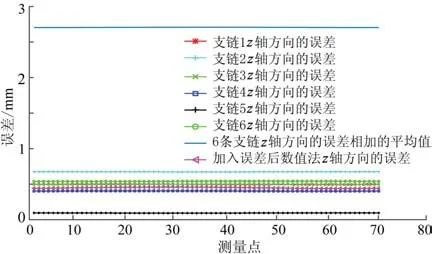
图13 Stewart机构z轴误差

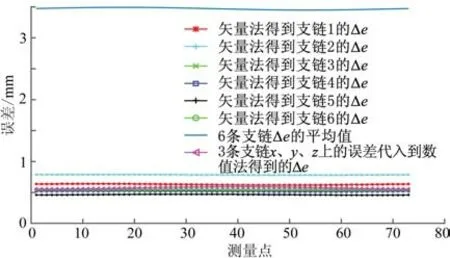
图14 Stewart平均误差

3 结束语

本文针对一种三自由度并联机构，将不同的误差代入各条支链模型中，从而计算出各条支链误差。并联机构正解方法一般为解析法和数值法，本文将计算出的各条支链的误差用不同的方式代入到正解中，可以得到含有误差的末端点位置。对比两种不同的带有误差的正解末端点，发现其基本一致，从而相互验证将误差加入正解中得到各条支链耦合后机构末端点的位置误差。其次，分析Stewart机构的误差模型，并将带有误差的各条支链代入到数值法中，得到含有各条支链误差耦合的Stewart末端点位置误差。最后，分析了两类耦合后的机构，发现通过耦合后，末端点的误差远远小于各条支链的误差和，说明并联机构本身可降低各条支链的误差。