基于排队论水平循环吊篮式立体车库存取车策略研究

杨剑尧，肖志权

（武汉纺织大学机械工程与自动化学院，武汉 430200）

0 引言

立体车库作为一种高自动化的设备，是一种集存车、取车一体化的智能化综合性系统，目前的结构形式主要有垂直循环式、巷道堆垛式、垂直升降式、水平循环式等[1]。随着立体车库的发展，研究其存取车策略、如何提高车库的运行效率、减少顾客等待时间等问题，成为众多学者研究的课题[2－3]。如陈桢等[4]利用遗传算法对立体车库库位的分配策略进行了研究；鲁立等[5]提出社会最小等待时间的出入库优化算法，将其应用于存取车策略优化；张芳芳等[6]基于排队论对升降横移式立体车库控制策略进行了研究；杨晓芬等[7]建立存取策略数学模型，并获得了车库不同存取策略下的存取车时间。由于不同形式的立体车库的工作原理及所选用函数的不同，其存取车策略和结果也会相应地不同。

基于排队论的理论原理，以水平循环吊篮式立体车库为研究对象，相对传统方式的自动化立体车库，只是将车辆随机地存入和取出，而利用排队论建立不同的存取策略数学模型，并分析在不同实际存取车情况下（存远大于取、存取相当、存远小于取）的车辆平均存取时间，确定较优的车辆存取方式，为车库的存取控制和管理决策提供参考。

1 水平循环吊篮式立体车库类型及结构特点

水平循环类立体车库的运行特点是利用一个水平循环运动的车位系统存取车辆，适宜建于地形狭长的场所，既减少了进出车道，又提高了土地利用率[8]。水平循环类立体车库可分为方形循环类立体车库和圆形循环类立体车库两大类。方形循环类循环系统以方形运动的方式实现上下层车位的交换，这种形式的循环系统需要两台驱动电机；圆形循环类循环系统以圆形运动的方式实现上下层车位的交换，这种形式的系统只需要一台驱动电机，对制造成本的控制有一定减少。

以圆形循环类立体车库中的水平循环吊篮式立体车库为研究对象，该类车库的许用高度或深度较小，适用于狭长场所，对地形适用性强。其车库结构示意图如图1所示。在牵引构件链条上，每隔一定距离安装一个载车吊篮，通过电机的减速转动带动传动机构，动力系统的传导使链条系统水平循环转动。在循环运动过程中，载车吊篮也将随着链条做循环运动，从而实现车位之间的交换。

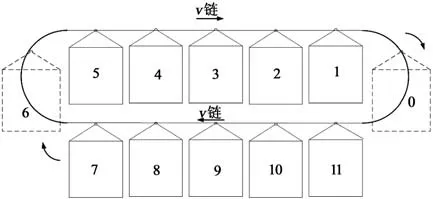
图1 12车位吊篮式立体车库停车设备示意图

2 存取车模型建立

2.1 存取车策略

排队论概述及存取策略排队论是研究要求获得某种服务的对象所产生的随机性聚散现象的理论，其广泛应用于服务系统，常出现于医院、银行、火车售票等场所。排队论的目的是为建立正确设计与有效运营决策系统的数学模型提供必要的科学依据，为管理者在系统服务管理决策上提供有利参考[9－10]。

根据水平循环吊篮式立体车库的物理框架结构特点，考虑到车位的随机分配以及车辆每次所存取的车位不同的问题，以车库存取系统存取车位总时间最少为目的，其中对选择最优存取车位的方法是以选择离存取出入口最近的目标车位，以其到达出入口的最短时间为选择原则，从而实现存取系统总时间最短的目的。

存取车策略分为3种，定义如下。

（1）存车优先策略。当用户完成存取车操作后，不论存取，系统通过计算将离存取车出入口最近的空车位转动到出入口处，以供下一位用户直接存入，无需等待。

（2）交叉存取策略。当同时几位用户需要存取车操作时，若前一位用户为存车操作，本次系统将变为取车策略，下一次系统将变为存车策略；若前一次用户为取车策略，存取原理与前者相同，依次循环交叉存取，其中存取都通过系统的计算选取最优的车位（如存车时，选取最近的空车位）。

（3）原地等待策略。当用户完成存取车操作后，车位将原地不动，等待下一位用户进行存或取车操作，其中对最优车位的选择方式为若用户进行存车操作时，系统将选取离出入口最近的空车位。

2.2 存取车策略排队模型

车库作为一个典型的随机离散排队服务系统，排队论也同样适用于车库服务系统，用户存放时间和操作时间都是离散变量，车库存取系统时间的确定同时与所选取的车位有关。车辆的存放时间和操作时间都为单一互不影响的变量，可以假定为符合泊松流分布的随机变量，泊松分布定义为：

式中：λ为单位时间内客户出现的平均次数；P( N＝k)为单位时间内客户出现k次的概率。

不同的存取车策略在不同的存取车场合的存取效率也各不相同，在车辆流量较大的场所，如繁华中心的写字楼，上下班时段就会出现不同的存取情况（上班时段，存车比取车多；下班时段，取车比存车多）。现实的车辆存取情况按车流量可分为3个时段：存车高峰（存远大于取）、存取车数量相当（存取相当）、取车高峰（存远小于取）。不同存取策略各有优势，适应不同的存取场合，为了在不同的时段选择出适用于该时段的存取车策略，以存取车总时间为目标函数，对存取车策略进行选择。具体参数说明如表1所示。

表1 参数说明

2.3 存取车策略数学模型

2.3.1 存车优先策略数学模型

按该种策略，用户选择第n车位号进行存（取）车操作时，存取1次所用时间t(n)为：

存取k次所用的总时间∑t为：

式中：k(n)为存取k次后共存取n车位号的次数。

2.3.2 交叉存取策略数学模型

交叉存取策略的存取时间与前一次、当前次以及下一次用户的存取选择有关，所以存取顺序和存取组合也会有不同的改变。

当前一次为存车操作，本次为取车操作，下一次将会是存车操作，其所用时间ta为：

当前一次为存车操作，本次为存车操作，下一次将会是存车操作，其所用时间tb为：

当前一次为取车操作，本次为存车操作，下一次将会是取车操作，其所用时间tc为：当前一次为取车操作，本次为取车操作，下一次将会是取车操作，其所用时间td为：

存取k次所用的总时间∑t为：

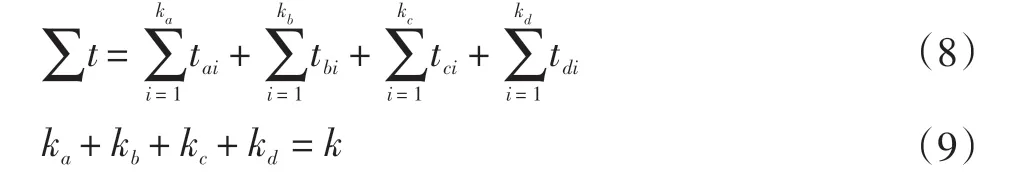
式中：tiq为用户存车过程中选择最优车位所用时间；tic为用户取车过程中选择最优车位所用时间；ka、kb、kc、kd分别为不同情况下对应的存取次数。

2.3.3 原地等待策略数学模型

原地等待策略存取时间与前一次和当前次用户的存取选择有关，存取的组合也不同。

当前一次为存车操作，本次为取车操作，然后吊篮就会原地等待下次用户操作，

其所用时间te为：

当前一次为存车操作，本次为存车操作，然后吊篮就会原地等待下次用户操作，

其所用时间tf为：

当前一次为取车操作，本次为存车操作，此时直接存车，其所用时间tg为：

当前一次为取车操作，本次为取车操作，然后吊篮就会原地等待下次用户操作，

其所用时间th为：

存取k次所用的总时间∑t为：式中：ke、kf、kg、kh分别为不同情况下对应的存取次数。

3 数学模型仿真分析

基于排队论的基础，利用MATLAB编写不同情况下的存取车策略的存取时间，用于计算和选择不同条件下的最优存取车策略。

调用MATLAB中Poissrnd函数生成用户存取时间t1序列和用户操作时间t2序列，分别服从参数为λ1和λ2的泊松分布，再调用Randi函数生成当前次存车序列c和取车序列j，将序列c与序列j重新组合并调用Randperm函数，将序列重新打乱生成当前次随机存取序列w。其中“1”为存车，“2”为取车；利用相同的原理生成前一次的存取车序列d和初始化车库中有无车序列m，将上述数据作为输入数据；其中调用Find函数对存取车过程中对最优车位（如存车时选择离出入口最近的空车位）进行选择。其程序流程框图如图2所示。

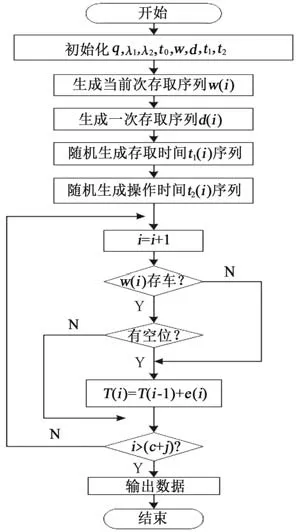
图2 程序流程

在车库初始化的基础上，分别模拟了3个时段的3种不同存取车策略的存取情况，设定存取车次q＝60、λ1＝40、λ2＝30；其中当前次存车序列c和取车序列j中的元素数量之和为60；而由MATLAB中Randi函数生成的当前次存取车序列w与前一次存取车序列d之间并不是没有关联，当前次的存取情况将成为下一次用户操作的前一次存取情况，所以将当前次存取序列w的存取情况相应存入到前一次存取序列d中。

设置参数存车序列c和取车序列j的元素数量分别为40和20，分别为存车数量和取车数量，模拟出存车高峰期时段（存远大于取）情况，其存取车总时间如图3所示。由图中的仿真结果可以看出，在车辆存车高峰时期3种策略，存车优先策略平均存取时间为82 s，交叉存取策略平均存取时间为56 s，原地等待策略平均存取时间为65 s，原地等待存取策略相对存车优先策略平均节约20.7%的时间，而交叉存取策略相对原地等待策略平均节约13.8%的时间。

图3 存车远大于取车总时间散点图

设置参数存车序列c和取车序列j的元素数量分别为31和29，分别为存车数量和取车数量，模拟出存取车数量相当（存取相当）情况，其存取车总时间如图4所示。由图中的仿真结果可以看出，在车辆存取相当时期3种策略，存车优先策略平均存取时间为91 s，交叉存取策略平均存取时间为87 s，原地等待策略平均存取时间为77 s，交叉存取策略相对存车优先策略平均节约4.4%的时间，而原地等待存取策略相对交叉存取等待策略平均节约11.5%的时间。

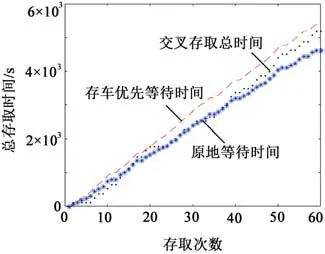
图4 存取车相当总时间散点图

设置参数存车序列c和取车序列j的元素数量分别为20和40，分别为存车数量和取车数量，模拟出取车高峰期时段（存远小于取）情况，其存取车总时间如图5所示。由图中的仿真结果可以看出，在车辆取车高峰时期3种策略，存车优先策略平均存取时间为148 s，交叉存取策略平均存取时间为113 s，原地等待策略平均存取时间为107 s，交叉存取策略相对存车优先策略平均节约23.6%的时间，而原地等待存取策略相对交叉存取等待策略平均节约5.3%的时间。

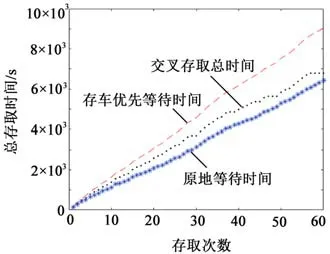
图5 存车远小于取车总时间散点图

综上所述，不同情况下的不同存取策略之间的差别较为明显，在存车高峰时，交叉存取策略要优于另两种策略，但交叉存取策略较原地等待策略差别不大；在其他两种车辆存取情况下，原地等待存取策略要优于另两种策略。

4 结束语

机械立体车库的应用为日益增加的机动车停车难问题提供了有效的解决途径，为适应多种停车场所，水平循环式立体车库也相继发展出现，而立体车库的不断发展，自动化程度也越来越高。考虑到管理者的管理决策以及用户的存取车体验，本文以水平循环吊篮式立体车库为研究对象，基于排队论的理论原理，对车库的存取车策略进行研究，希望能够为提高车库的存取效率提供参考。