高空滑索运动仿真分析
2021-07-14王英杰罗金良
王英杰,罗金良
(南华大学机械学院,湖南衡阳 421001)
0 引言
轨道滑索是一类中小型的游乐项目。在开始阶段,将机械设备和游戏者置于最高点,并给予一定的初始速度,设备与游戏者将在重力的作用下,沿着轨道滑落直至停止。此类设施,运动速度较快、刺激性强,深受青少年的喜爱。然而,在追求刺激与享受的同时,此类游乐设施的危险性也在成比例增加。近年来,游乐设施安全事故频繁发生,作为一种特种设备,其安全事故往往非常严重,造成的社会影响也很恶劣[1-3]。因此,设备的安全性与稳定性一直是设计者们关注的问题。目前对于游乐设施的研究已经比较成熟,在十几年前运动学和动力学仿真技术就已经应用在游乐设施设计阶段[4]。滑索轨道作为一种游乐设施,在考虑设备自身结构稳定的同时,还需要考虑游乐设施对游客自身安全的影响。
本文将高空滑索轨道作为研究对象,将预设计的轨道简化为一条空间曲线,并建立滑行器的动力学模型,通过MATLAB计算,对滑行器在轨道上的运动特性进行分析研究。通过此方法来分析轨道,不需要建立准确的滑索轨道和滑行器的三维模型,相较于ADAMS运动仿真更加便捷高效。
1 轨道滑索建模
轨道滑索系统由固定曲线型轨道和滑行器组成,滑行器可在曲线轨道上从高处到低处惯性滑行。
1.1 滑索轨道建模
滑索轨道的初步设计必须考虑滑索轨道周围的地理环境以及满足人体安全规范的速度、加速度安全规范等因素。本文建立的轨道滑索曲线几何模型如图1~3所示。滑索轨道主要由水平区、下降区、缓冲区3个部分组成,最大高度差为7.8 m。在水平区,系好滑行器后,给予游客一定的初始速度,在重力作用下,游客在下降区自由下落至最低点处,并于缓冲区减速并停止。

图1 滑行轨道正视图Fig.1 Front view of sliding track

图2 滑行轨道侧视图Fig.2 Side view of sliding track

图3 滑行轨道俯视图Fig.3 Top view of sliding track
为方便MATLAB计算,将滑行轨道简化为一条样条曲线。将样条曲线均分为10 000段,计算滑行器在通过每段曲线末尾时的速度、加速度以及所需要的时间曲线。
1.2 滑行器建模
滑行器由车架、主轮轮组、侧轮轮组等部件组成,如图4所示。车架与主轮及侧轮轮组连接,提供前进向的滑行自由度。车架下方悬挂保险带座椅,可以限制性地摆动。滑行器通过行走轮组与曲线轨道接触连接。
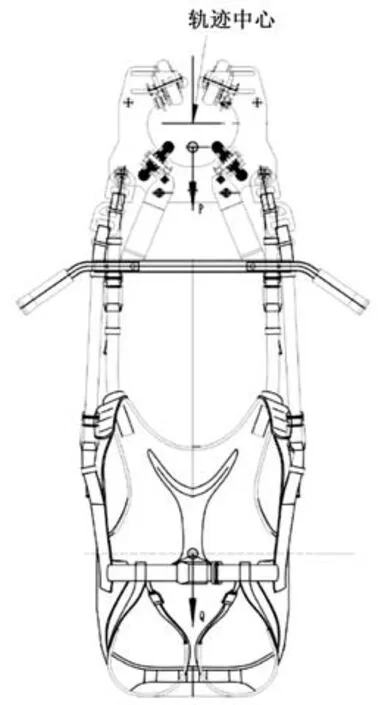
图4 滑行器三维模型Fig.4 3D model of glider
2 轨道滑索动力学模型
滑行器从高处到低处惯性滑行,经过弧形轨道时,滑行器会对运行轨道产生离心荷载,产生惯性冲击。通过对轨道滑索的动力学分析,可优化轨道滑索结构设计、曲线轨道弯曲半径设计。通过分析轨道滑索的动力特性,设计时可提高乘客乘坐的安全及舒适度。
计算滑行器从第i到i+1点的速度,根据滑行器的能量守恒定律[5],i计算点:

式中:Eid为动能;Eip为势能;m为滑行器及人体质量,kg;vi为i点滑行器滑行速度,m/s;g为重力加速度,9.8 m/s2;Hi为滑行器高度,m。
i+1计算点:

式中:Ei+1d为动能;Ei+1p为势能;Ei、i+1g为重力摩擦损失;Ei、i+1n为向心力摩擦损失;vi+1为滑行器i+1点速度,m/s;Hi+1为滑行器i+1点高度,m;cosγi、cosγi+1为滑行器法线(垂直于滑行轨道)方向余弦;si、i+1为滑行器i和i+1点重心轨迹线长度,m;Ri、Ri+1为第i点及i+1点曲率半径。
根据能量守恒定律:

结合式(1)~(7)可得:

曲线段的加速度为:

3 运动仿真计算
3.1 ADMAS运动仿真
滑索轨道在ADAMS中的建模不同于普通的实体建模,不需要建立与实际完全相同的物理模型,只需将滑行器行走轮中心的轨迹曲线作为ADAMS中的滑索轨道样条曲线。由于ADAMS中建立的滑索轨迹曲线只是为了模拟滑行器及人体的运动情况,因此不需要建立准确的滑索轨道立柱模型。之后,还需要对滑索轨道样条曲线添加对地面的固定约束,否则在后续仿真过程中,轨道曲线会在重力作用下竖直下滑。
ADAMS多体动力学分析可得出滑行器部件间荷载、相对速度及加速度关系。ADAMS运动仿真主要是对滑行器在ADAMS中进行建模并添加约束,施加载荷。其中滑行器的三维模型是通过SOLIDWORKS导入到ADAMS中,并且添加线性接触、固定、移动等约束。通过两对行走轮多点接触的模拟,还原滑行器在运动过程中的运行工况。行走轮与轨道曲线模型模拟接触,行走轮与滑行器模拟刚性固接,滑行器与座椅块铰接,并通过设置阻尼荷载模拟两部件间摩擦作用[6-7]。滑行器及人体相关的参数如表1所示。

表1 滑行器相关参数Table1 Relative parameters of the glider
本文选取滑行器座椅中心为测试点,人体坐标系为参考方向[8]。如图5所示,人体正前方为+X方向,竖直向上为+Z方向,左手方向为-Y方向。

图5 人体坐标系Fig.5 Human coordinate system
设置终止时间为50 s,步数为1 000,经过多次运动仿真,得到最符合实际滑行过程的运动特性如图6所示。

图6 滑行器速度、加速度曲线Fig.6 Speed and acceleration curves of the glider
在水平区域给予滑行器及人体初始速度2 m/s,使滑行器及人体在重力的作用下沿着滑索轨道呈顺时针下滑。根据图中ADMAS仿真所得的滑行器速度曲线可知,滑行器在下滑大约46 s时达到滑行轨道最低点,在大约48 s时缓冲结束。但由于滑行器自身在滑行器缓冲结束之时仍存在自身侧向摆动的速度,因此在滑行器停止前进时,滑行器的合速度不会随之减小到0。根据滑行器运动特性曲线,可以获得滑行器及人体在滑行轨道滑行至不同位置的加速度情况,由此可以计算出人体在该位置的受力情况[9-10]。
3.2 MATLAB运动计算与验证
利用MATLAB进行滑行器的运动计算,只需要获得滑行轨迹的空间坐标。滑行轨迹是一条不规则的样条曲线,将曲线尽可能多地均分为若干段(本次计算是将滑行轨迹样条曲线均分为10 000段),每段可以近似看成是平滑的圆弧,根据式(8)求得每一段的速度大小,再将所得的速度代入公式t=s/vˉ,计算出每一段所需要的时间,由此可以获得时间-速度曲线如图7所示。
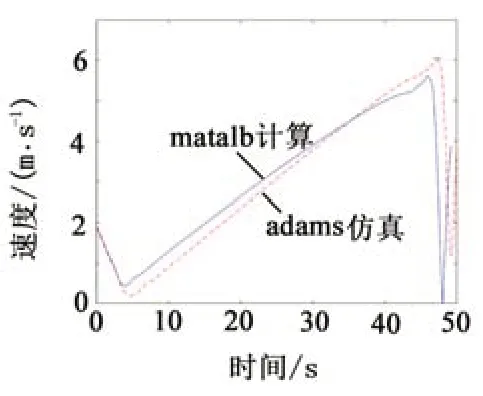
图7 滑行时间-速度曲线Fig.7 Sliding time-speed curve
将求得的速度代入式(9),求出加速度-时间曲线如图8所示。

图8 滑行加速度-时间曲线Fig.8 Sliding acceleration-time curve
通过MATLAB计算所得到的速度、加速度与滑行器滑行样条曲线上的点是一一对应的,因此可以进一步获得滑行器在不同位置处的受力情况。通过比较ADAMS运动仿真结果可以得知,MATLAB计算所得的滑行器运动特性曲线与ADAMS运动仿真求得的滑行器运动特性曲线基本一致,从而也验证了利用MATLAB计算滑行器运动特性这一方法的准确性。这一结果对于滑行轨道的设计具有很重要的参考意义,因而建立更加准确的滑行器动力学模型也更为重要。
4 结束语
本文根据预设计的滑行轨道的几何形状,计算出滑行轨道各段的长度、高度、曲率,采用ADAMS运动仿真和MATLAB计算两种方法,获得滑行器在滑行轨道不同位置处的运动特性曲线。结果表明,通过MAT⁃LAB求得的运动特性曲线与ADAMS仿真所求的运动特性曲线基本吻合,但是由于本文通过MATLAB方法计算的滑行器速度是沿着滑行轨道切向方向的,忽略了由于滑行器作曲线运动时产生的离心运动,因此也忽略了由于滑行器自身的侧向振动所造成的动能损失,因此本文所建立的滑行器动力学模型仍有很大的完善空间。
