基于和声搜索算法的公交线路规划方法研究
2021-07-14王景升
周 杨,王景升
(中国人民公安大学,北京 100038)
随着车辆保有量的增加,城市交通压力不断增大,交通管理部门对公共出行方式越发重视。公交系统作为城市公共出行系统的骨架,连接城市的不同分区,在整合城市资源、提高城市路网运行效率等方面起到了重要作用。公交线路设计优化需要解决居民换乘、等车耗时和公交运行成本等问题,涉及城市居民出行、便利、安全、环保和效益等方面,是城市公交系统的重点课题。我国关于公交线路的研究起步较晚,从20世纪80年代初开始,逐步形成建立数学模型,利用算法对模型求解的问题解决模式。
公交线路规划问题可以视作最优化问题,目前广泛使用的既有Dijkstra(迪克斯特拉)算法和Floyd(弗洛伊德)算法等最短路径算法,也有动态规划算法、蚁群算法、粒子群算法、遗传算法以及和声搜索(harmony search, HS)算法等全局性搜索算法。较为传统的最短路径算法可以与图论方法相结合,计算场景内节点之间的最短线路[1-2]。全局性搜索算法通过引入不同参数对模型进行调节,在计算量较大时,拥有更强的全局搜索能力[3-4]。在大数据智能化的条件下,融合遥感技术、电子信息技术等技术理论,分析现有城市交通公交线路节点,以确定公交线网的优化方向,例如:运营者运营成本最低,公交线路服务能力最大,居民换乘次数最少,出行时间最短等。再根据优化方向建立线路或线网优化的数学模型,结合约束条件选择算法求解,进一步分析结果,进而得出公交线路或线网优化方案。
但在实际应用过程中,部分算法表现出一些不足。最短路径算法无法同时考虑换乘次数和服务人数等问题,在解决多目标决策问题时表现不佳;智能搜索算法依赖参数设置,在不同适用条件下的计算能力有所差异,如:遗传算法扩展性大,搜索能力强,但计算空间有限,易早熟收敛,形成局部最优[4];粒子群算法只利用最优粒子传递信息,计算速度快,但缺乏速度的动态调节,易导致收敛精度低或不易收敛,不能有效解决组合优化问题。
本文利用和声搜索算法,基于不同算例和约束条件进行公交线路规划计算,并通过与遗传算法计算结果进行对比,验证其实用性。
1 和声搜索算法
和声搜索算法是一种新近问世的启发性全局搜索算法。灵感源自乐师创作和声的过程。在音乐演奏中,乐师凭借记忆对不同乐器发出的音调进行选择性调整,最终获得“完美和声”。Zong等[5]首先提出和声搜索算法,该算法结构简单、需要调整的参数少、求解速度快、鲁棒性强、全局搜索能力强且通用性高,在解决组合优化问题上具有优势。
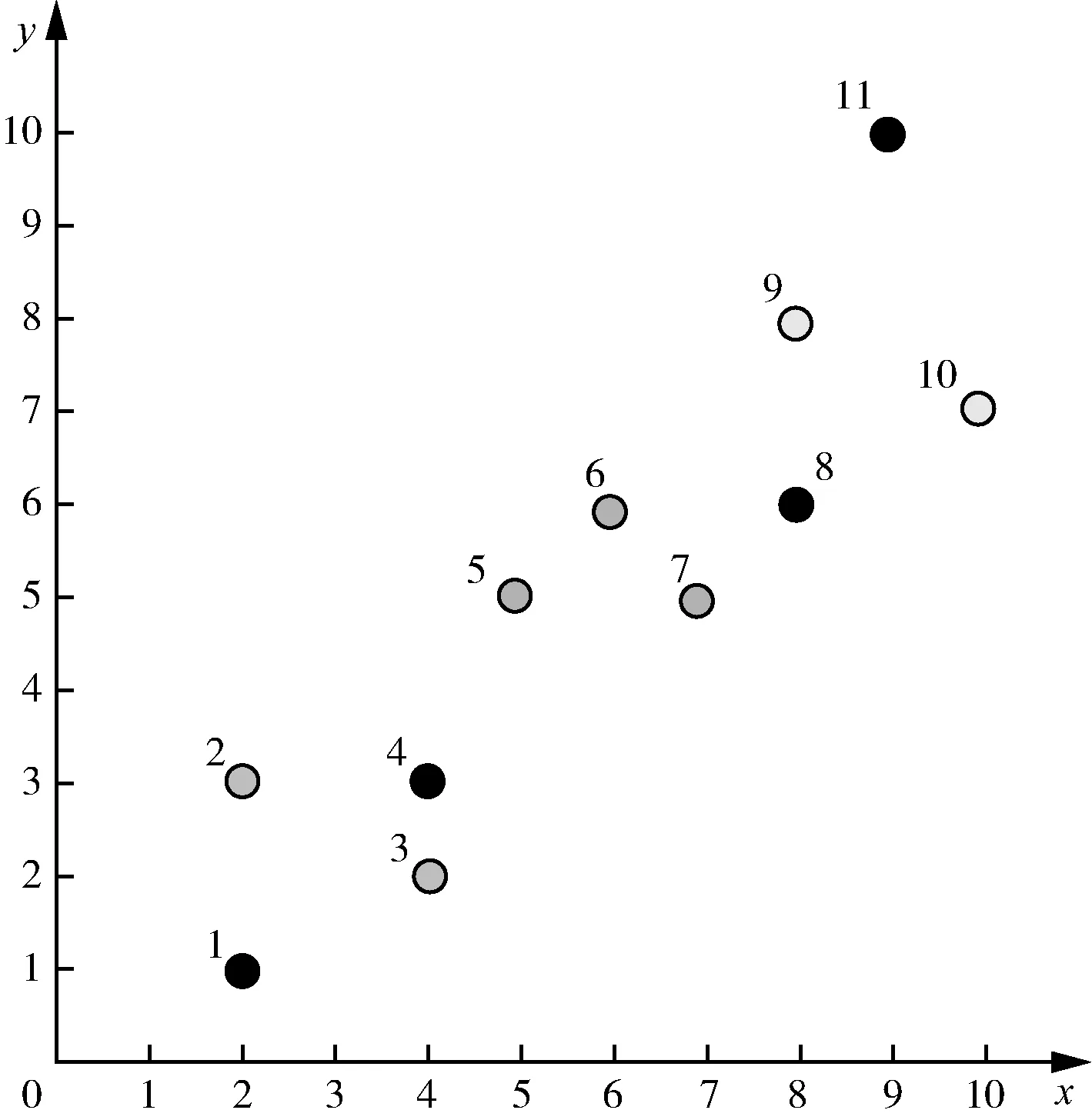
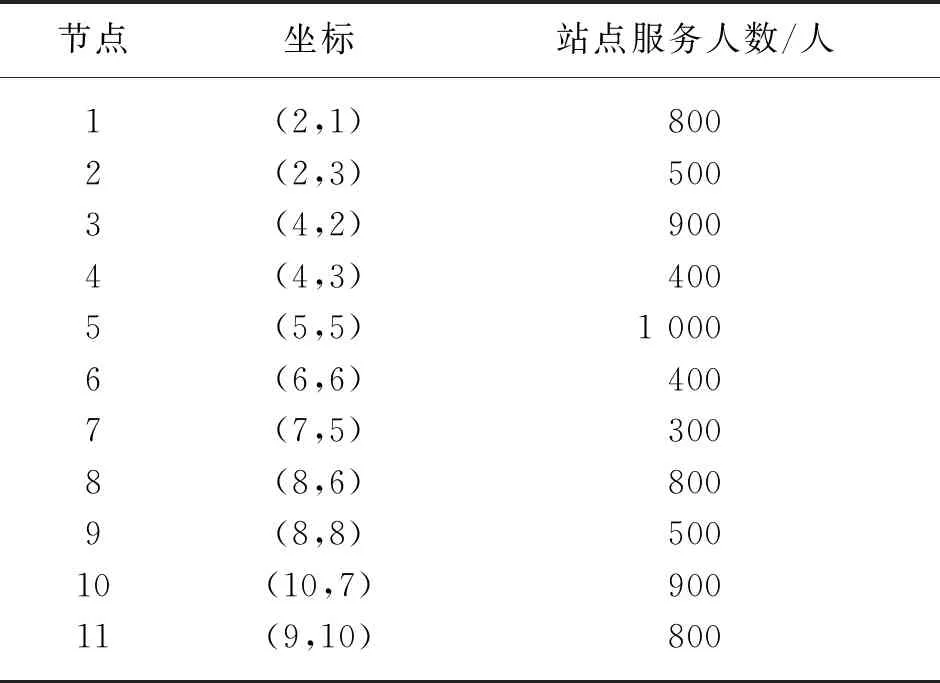
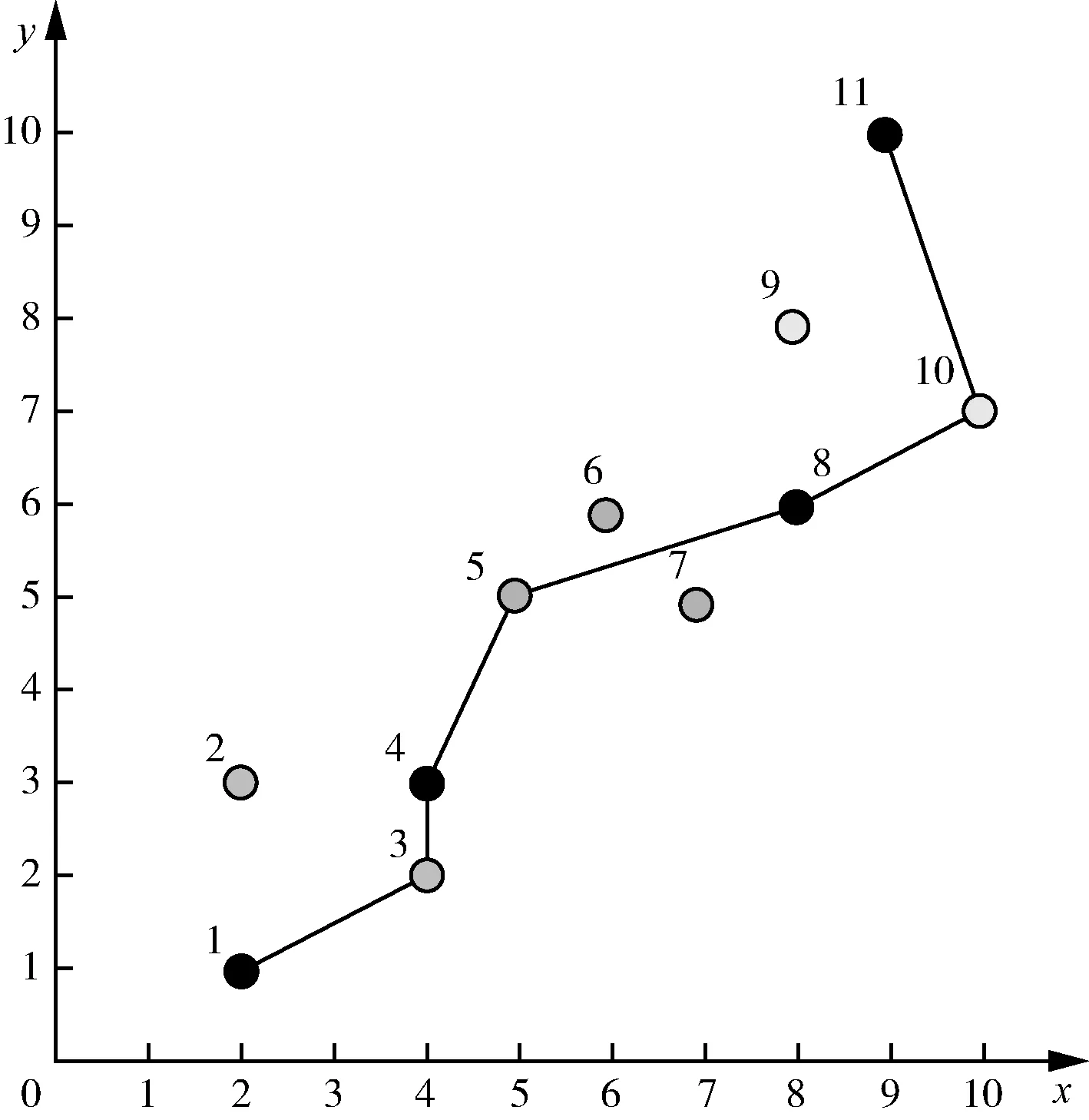
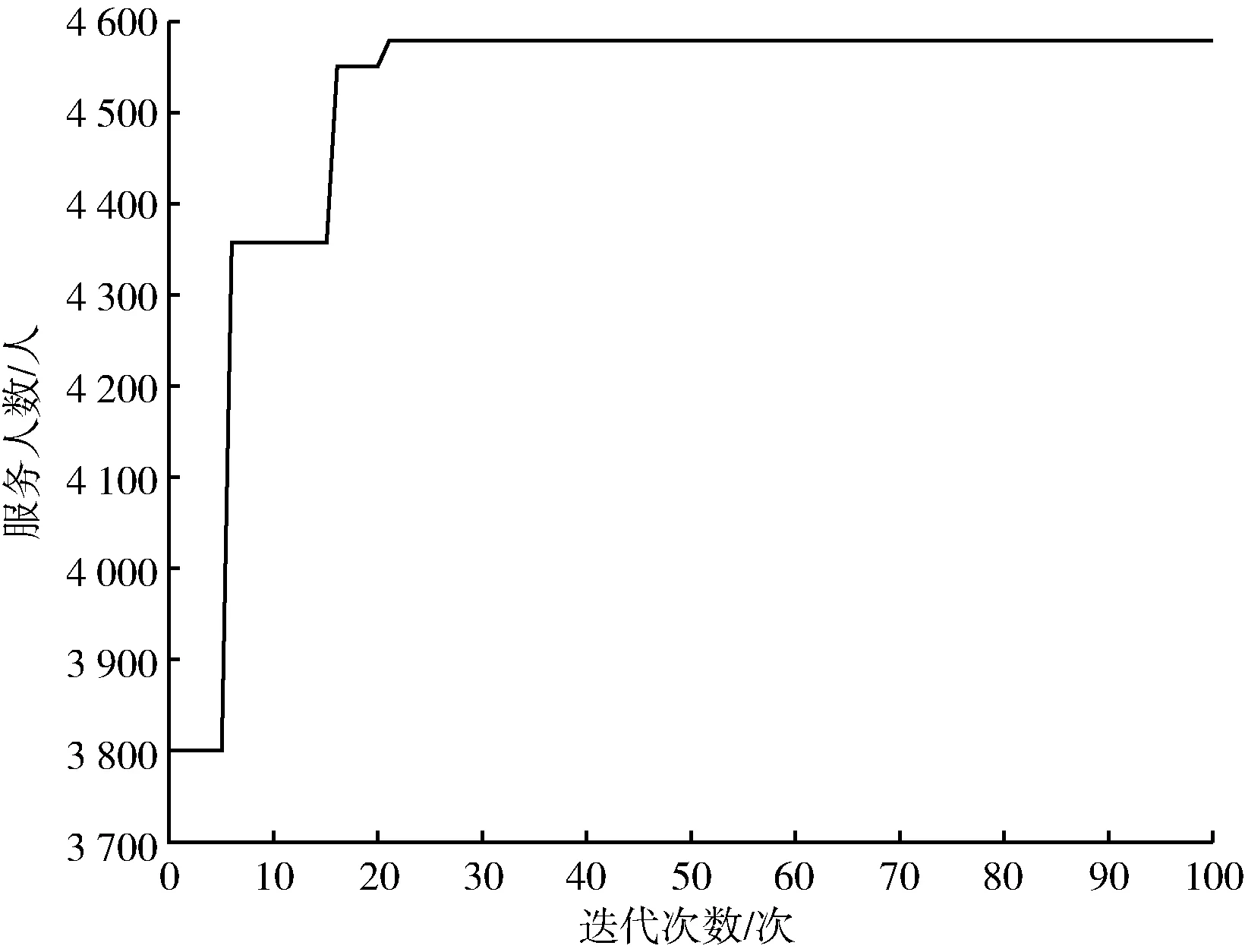
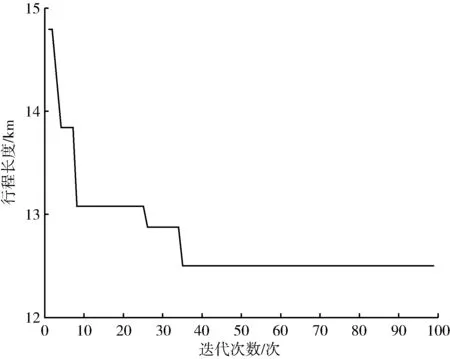
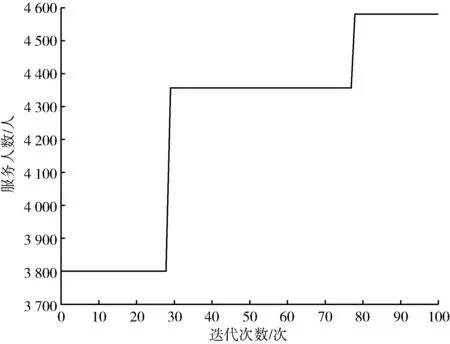
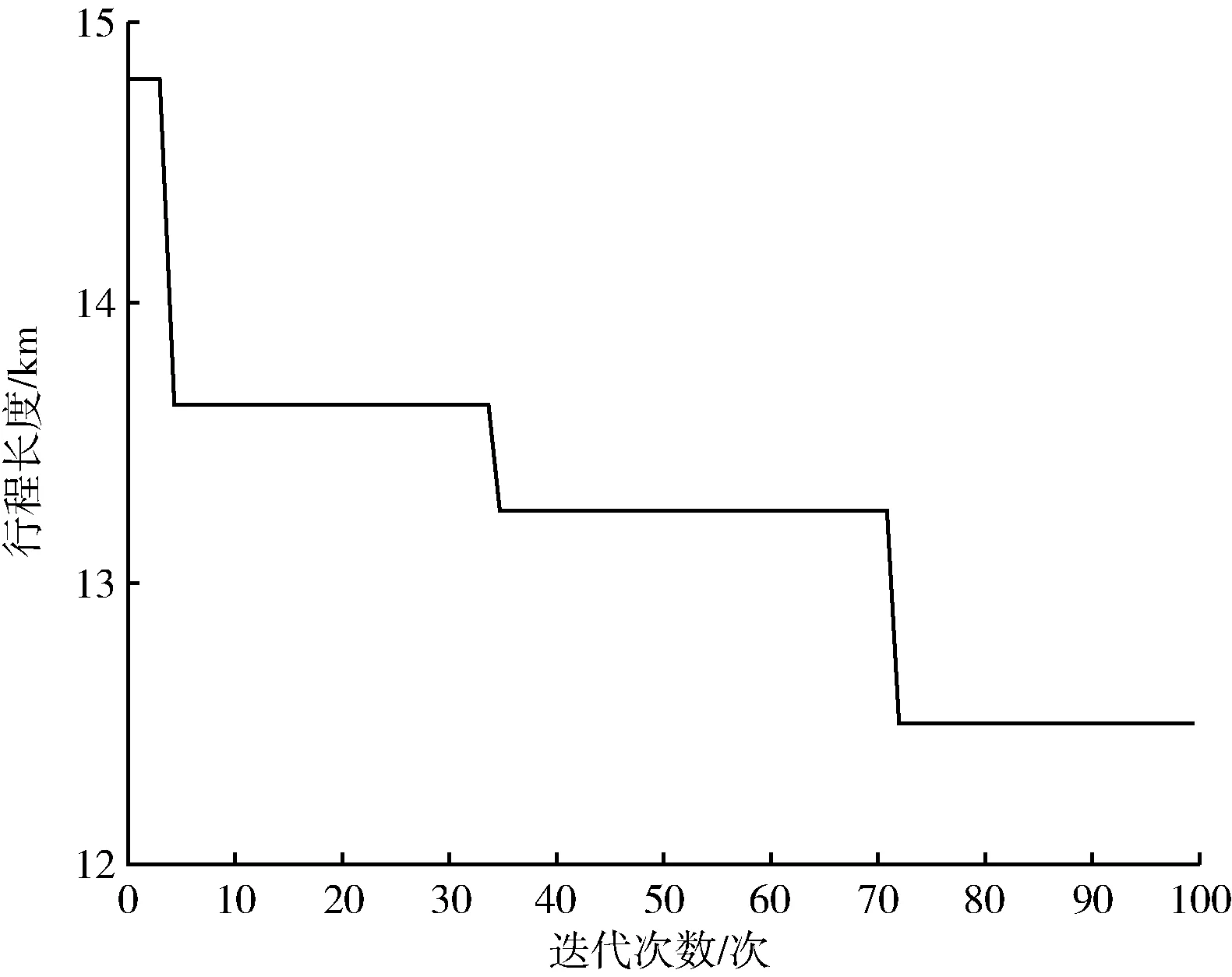
算法将乐器i(i=1,2,…,n)类比为目标方案中的第i个变量,产生的和声Hj(j=1,2,…,n)视为优化问题的第j个解向量,对和声的评价即为目标函数的函数值。算法首先产生HMS(harmony memory size,和声记忆库大小)个解,将其放入和声记忆库(harmony memory,HM),类比乐师的初始记忆,作为目标方案的初始解。之后随机产生(0,1)的参数rand1和rand2,并引入和声记忆库取值概率(harmony memory considering rate, HMCR)和微调概率(pitch adjusting rate,PAR)。若rand1 有别于其他启发式算法,和声搜索算法的优势在于其包含记忆库计算、局部扰动与随机选择的即兴创作过程,在优化算法集约化与多样化的平衡中发挥了重要作用。 和声搜索算法的特征如下:①在所有可能存在的向量中生成新的向量。②针对向量中的每个决策变量进行单独考虑。③不需要对变量进行初始赋值。④算法中无进制转换,计算速度较快。 和声搜索算法流程如图1所示。 图1 和声搜索算法流程 城市公交线路具有停靠节点多、总里程短等特点。在二维坐标系中放置坐标,模拟公交节点,利用Matlab语言,分别以服务总人数M最大、总行程时间T最小为目标函数,采用Matlab 2019a编写和声搜索算法程序并进行计算。和声搜索算法对初始解的依赖性较大,且本试验算例的计算量较小,为避免过早陷入局部最优,因此和声记忆库及其取值概率较小,设置参数HMS为2,HMCR为0.3,PAR为0.1,bw为0.05,N为100。 坐标系节点设置如图2所示,其中点1、4、8、11为固定节点,点2、3、5、6、7、9、10为可以选择经过的节点。点1和点11为确定的起点和终点。 图2 坐标系节点设置 公交线路规划应将服务更多居民作为重要目标之一。当前研究成果中通常将公交站点服务人数作为重要计算指标[3],本试验对规划线路可能经过的节点进行居住人数赋值,路段服务人数计算见式(1)。 (1) 式中,Mi为路段服务人数,人;Pi为路段上各节点服务人数,人/km;Li为路段长度,km;i为节点。 线路服务人数的目标函数见式(2)。 (2) 式中,M为线路总服务人数,人。 节点坐标及站点服务人数如表1所示。 表1 节点坐标及站点服务人数 以每两个固定节点间路段的服务人数作为变量,输入坐标及节点服务人数矩阵,经过计算筛选,得出符合条件的最优路径为1-3-4-5-8-10-11,最大服务人数为4 582人。服务人数最大路径(HS)如图3所示,服务人数适应度曲线(HS)如图4所示。 图3 服务人数最大路径(HS) 图4 服务人数适应度曲线(HS) 模型中的行程时间由换乘时间和行驶时间组成,假设换乘时间为定量,与上下客人数无关。行驶时间为行程长度与平均车速之比。行程时间的目标函数为 (3) 式中,T为行程时间,min;D为公交线路行程长度,km;d(i-1,i)为从第i-1个节点到第i个节点的距离,m;n为最后一个经过的节点;v0为城市公交平均车速,km/h,取35 km/h;t0为平均停靠换乘时间,min,取3 min。 公交线路规划问题属于多目标决策问题,本试验中的不同目标之间具有相对独立性。根据《城市综合交通体系规划标准》(GB/T 51328—2018)[7],公共交通线路非直线系数不得大于1.4,即目标函数的约束条件为:D≤1.4×d(0,n)。 不同目标路径结果如表2所示。 表2 不同目标路径结果 以图2场景中线路不固定的3个路段分别作为3个变量(乐器),通过对可选节点进行组合,并对不同组合结果下的路段长度对比选择,计算得到符合条件的行程最短路径为1-3-4-7-8-9-11,最短行程时间为39.414 7 min。总行程时间最短路径如图5所示,行程长度适应度进化曲线(HS)如图6所示。 图5 总行程时间最短路径 图6 行程长度适应度进化曲线(HS) 本试验采用遗传算法(GA)进行算法效果对比,在相同节点场景下,以相同大小的初始解集进行计算,遗传算法的参数设置如下:种群数Popsize为2,复制概率为0.3,交叉概率PC为0.4,变异概率PM为0.3,N为100。用Matlab进行编程,并绘制两种目标函数情况下的适应度曲线,服务人数适应度进化曲线(GA)如图7所示,行程长度适应度进化曲线(GA)如图8所示。 本试验场景较为简单,两种算法都能够在多次迭代后得到最优解,因此本文以迭代次数作为指标对比两种算法优劣。对比图4与图7,在以最大服务人数为目标函数时,HS约25次迭代后收敛,GA约80次迭代后收敛;对比图6和图8,在以最短行程时间为目标函数时,HS约35次迭代后收敛,GA约75次迭代后收敛。相较于遗传算法,和声搜索算法采用十进制编码,原理简单,容易实现。 图7 服务人数适应度进化曲线(GA) 图8 行程长度适应度进化曲线(GA) 本文以假设条件下的最短行程时间与最大服务人数为约束条件,基于和声搜索算法提出公交线路规划方法,结合算例,对约束模型下的起讫点及部分节点固定的公交线路进行计算筛选,采用遗传算法对同一场景编程计算作为对照。对比试验结果表明,和声搜索算法在收敛速度上明显优于遗传算法,相较于遗传算法的二进制编码,和声搜索的十进制编码方式更适合进行快速计算。和声搜索算法作为最新的智能优化算法,在固定节点公交线路的规划问题上,具有可参考性,类似的规划方法可用于解决班车、校车和定制公交等路线规划问题。 相较于其他常用的最优化算法,和声搜索算法的参数设置较为简单,一般依靠经验确定,在计算量较小的前提下,尝试不同参数可在一定程度上避免陷入局部最优,但在较为复杂的问题上缺乏理论指导,因此,在参数的选择、不同选参条件下的结果对比以及通过融合其他智能优化算法的思想进行算法改进等方面值得深入研究。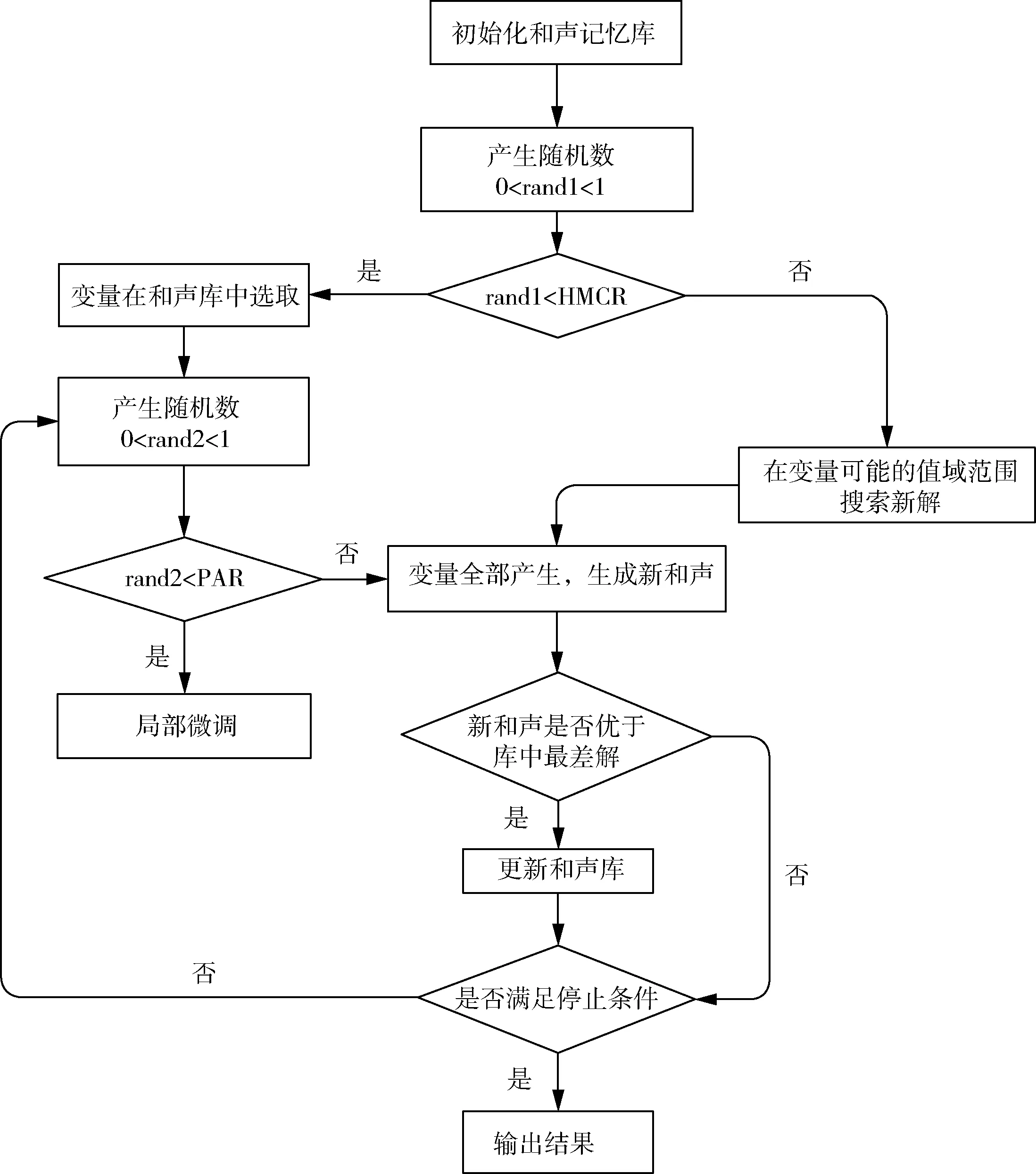
2 线路规划的数学建模与计算
2.1 服务人数
2.2 行程时间
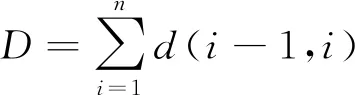


2.3 遗传算法对比
3 总结
