智能汽车仿人转向控制驾驶员模型分析
2021-07-14江浩斌周新宸李傲雪
江浩斌,周新宸,李傲雪
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
随着人工智能与传感器技术的飞速发展,具有高级别驾驶辅助功能甚至自动驾驶功能的智能汽车在不久的将来会越来越多地成为人们出行选择.因此,具有自主驾驶能力的智能汽车将会与人类驾驶员驾驶的汽车共同行使在道路上[1].为了减轻人类驾驶员在面对周围具有自动驾驶功能的智能车辆的不适感,有必要提出一种具有人类驾驶员,特别是熟练驾驶员,操控特征的驾驶员模型,即仿人驾驶员模型.
根据模型输出量不同,可将驾驶员模型分为速度控制、转向控制和速度转向综合控制驾驶员模型[2].本研究的仿人转向控制驾驶员模型属于转向控制驾驶员模型.
转向控制驾驶员模型的构建主要分为参考系统的选取和转向盘转角的生成2个部分.参考系统是指被控车辆在行驶过程中,需要跟踪的目标点或目标方向,一般可以分为非前瞻式参考系统与前瞻式参考系统[3-5].采用非前瞻式参考系统所构建的驾驶员模型通过计算车辆附近的期望路径与自身坐标之间的侧向偏差或是航向角偏差来控制车辆实现道路跟踪.前瞻式参考系统则是通过测算车辆前方期望道路与车辆自身行进方向上的侧向偏差或是航向角偏差来实现自动转向,其过程类似于人类驾驶员开车过程中的预瞄行为.区别于非前瞻式参考系统中目标点仅位于车辆当前位置附近的期望路径上的1点,前瞻式参考系统中的目标点可以为前方路径上的1点(单点预瞄[6])、2点(2点预瞄[7])或多点(多点预瞄[8]).1992年至1993年间H.PENG等[4]通过实车试验验证了基于2种参考系统的道路跟踪方法的控制精度.结果表明:当车速为50 km·h-1以下时,车辆能够很好地完成路径跟踪任务;当车速高于50 km·h-1时,必须引入以预瞄控制为基础的前馈控制量.此后针对自动驾驶车辆转向控制驾驶员模型的研究也大多基于前瞻式参考系开展.
对于转向控制驾驶员模型,转向盘转角生成方式主要可分为基于道路几何与运动学的生成方式、基于动力学的生成方式和基于智能算法的生成方式[5].基于道路几何与运动学的方法常根据Ackerman转角关系来推导车辆转向盘转角,其中较为著名的是纯跟踪算法[9]以及郭孔辉[6]提出的最优曲率预瞄驾驶员模型.后者在前者的基础上引入了车辆运动学的推导过程,赋予了模型中各个参数的物理意义.为进一步提升模型的轨迹跟踪性能,基于动力学的转向盘转角生成方式通过引入车辆线性或非线性运动学模型来推导车辆的转向盘转角[10-11].这种方式虽然能改善驾驶员模型在高速或复杂路面情况下的跟踪性能,但复杂的动力学模型会对控制系统的计算能力有一定的要求.基于智能算法的转角生成方式主要可以分为2类:① 将智能算法与传统的基于动力学或运动学的驾驶员模型相结合,动态调整或最优化驾驶员模型的预瞄距离或是求解转角过程中的权重系数从而提升原有驾驶员模型的控制性能[12-13];② “端到端”的转角生成方式,即采用自然驾驶数据训练的方式,直接将前方道路信息通过神经网络生成转向盘转角从而完成对车辆的转向控制[14].基于智能算法的转角生成方式,特别是“端到端”的转向控制方法,似乎完全再现了人类驾驶员驾驶时的决策过程(直接由前方路面信息推测出车辆转向盘转角),但其对于训练样本的要求较高.在实际驾驶过程中,当遇到训练样本之外的工况时,这种转角生成方式可能存在一定的隐患.
综上所述,在前瞻式参考系统下,基于道路几何与运动学的转角生成方式,因其结构简单且不需要建立复杂的动力学模型就可以完成车辆的转角控制,而广泛应用在实际场合中[15].学者们通过进一步模拟人类驾驶员预瞄行为,如动态决策预瞄距离[16]、采用注视切点的远近两点预瞄行为进行模型构建[17]等方法提升了该类模型的控制性能.上述改进虽然提升了模型的控制精度,但并未与人类驾驶员的实际操纵结果进行比较.
笔者基于最优曲率预瞄驾驶员模型与T-S模糊推理算法,提出一种预瞄点横向与纵向自适应调节的仿人转向控制驾驶员模型.在一封闭城市双车道弯道工况下采集熟练驾驶员驾驶数据,并分析得出仿人驾驶员模型训练目标,通过蚁群算法优化得出仿人驾驶员模型的预瞄点决策规则.对比研究最优曲率预瞄驾驶员模型、预瞄距离自适应调节驾驶员模型、仿人驾驶员模型同熟练驾驶员间行驶轨迹的相似程度.
1 仿人转向控制驾驶员模型
提出的仿人转向控制驾驶员模型由如下2部分组成:基于最优曲率预瞄驾驶员模型构建的转角求解模块和基于T-S模糊推理系统构建的预瞄点决策模块.
1.1 最优曲率预瞄驾驶员模型
最优曲率预瞄驾驶员模型通过假设驾驶员在行驶过程中会通过转向行为使得车辆以一恒定曲率轨迹到达预瞄点,即最优曲率预瞄.为了便于仿真,采用转向半径的计算方法,如图1所示.
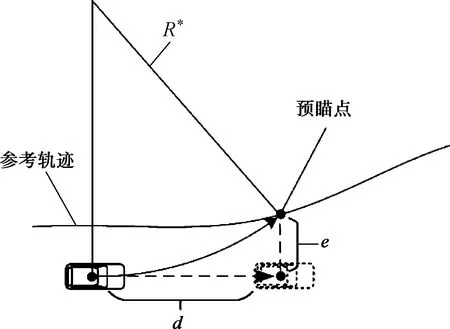
图1 最优转向半径计算
根据图1中的几何关系,基于最优曲率理论的车辆转向半径为
(1)
式中:d为预瞄距离,定义为车辆与预瞄点在当前行进方向上的距离;e为侧向偏差,定义为预瞄点到车辆行进方向上的侧向距离.
在低速小转角的工况下,车辆的转向半径R与转向盘转角δsw之间近似满足Ackerman关系,即
(2)
式中:i为车辆转向传动比;L为车辆轴距.
结合式(1)与式(2),推算出的基于最优曲率理论的车辆理想转向盘转角为
(3)
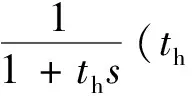
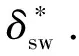
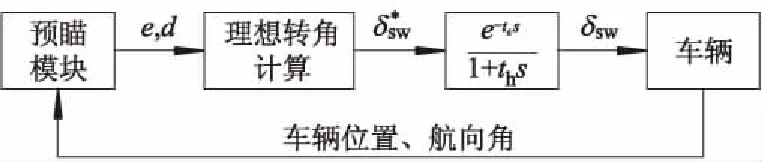
图2 最优曲率预瞄驾驶员模型
1.2 预瞄点决策模块
文献[16]中说明驾驶员的预瞄距离应随车辆速度、道路曲率等条件变化.早期关于弯道视觉注视机制的研究表明,驾驶员在弯道行驶时会注视前方道路的内沿切点(tangent point,TP)[18].K.D.ROBERTSHAW等[19]利用眼动仪采集并分析驾驶员实际注视点数据.试验结果表明,驾驶员在弯道行驶过程中所采取的注视点并不始终为TP,而是会在道路横截方向呈现一定特征分布.
上述研究成果表明,人类驾驶员在弯道行驶时,预瞄点在车辆纵向以及横向上均会发生变化.为模拟人类驾驶员这一特征,本研究构建的驾驶员预瞄点调节机制如图3所示.
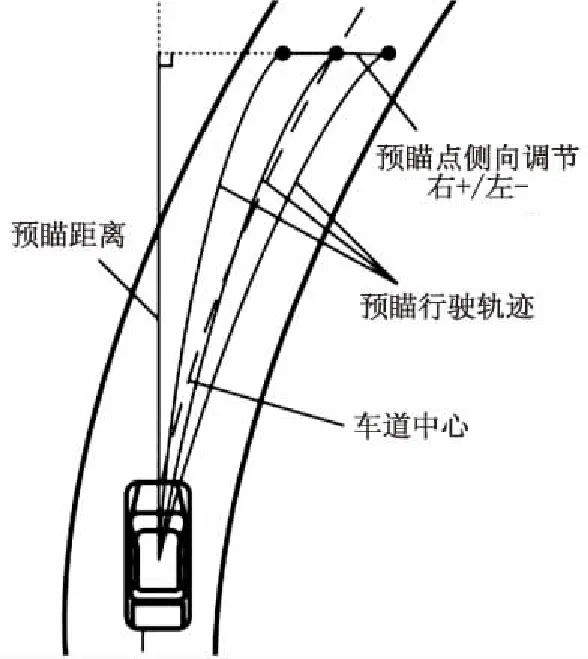
图3 驾驶员预瞄点调节
驾驶员的预瞄点由预瞄距离d与预瞄侧向调节值dl决定.d的变化体现了驾驶员对于预瞄点在纵向位置的调整.dl为车辆当前车道中心上的预瞄点在垂直于车辆航向方向上调整的距离(向右调节为正,向左调节为负),其值的变化体现了驾驶员对预瞄点在横向位置上的调整.
重点研究的是转向控制驾驶员模型,为了排除速度控制的影响,假设车辆以恒定车速通过弯道.综合相关学者的研究结果,在恒定车速下,对驾驶员预瞄点调整行为提出如下假设:① 驾驶员会根据车辆在道路上的位置状态(车辆当前的侧向偏差、偏差的变化速度等)对预瞄点纵向位置进行调节[16];② 道路类型(直路或弯道)会影响驾驶员预瞄点的纵向和横向位置[19];③ 在弯道行驶时,预瞄点的横向位置会受纵向位置影响[17].
针对以上假设,采用0阶T-S模糊算法[20]构建预瞄点决策模块.该模块由纵向和横向预瞄模糊决策模块组成.纵向预瞄决策模块的输入量为车辆当前质心位置与车道中心的侧向偏差ev,车辆当前航向角偏差eα(表征侧向偏差的变化速度),车辆当前位置的道路曲率ρ.横向预瞄决策模块的输入量为ρ与d.对于纵向预瞄决策模块,模糊规则为
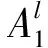

(4)
式中:μAi(·)为各输入量所对应的隶属度函数.
采用如图4所示的三角形式模糊隶属函数,其中车辆当前侧向偏差变化范围为ev∈(0,4)m,航向角偏差变化范围为eα∈(0°,10°),当前道路曲率变化范围为ρ∈(0,0.02)m-1.各输入量均划分为5个模糊子集,其中侧向偏差与航向角偏差为平均划分.对于道路曲率,考虑其为曲率半径的倒数的特征,按照曲率半径大于500 m(M1)、200 m至500 m之间(M2)、100 m至200 m之间(M3)、50 m至100 m之间(M4)和小于50 m(M5)所对应的曲率区间进行划分.
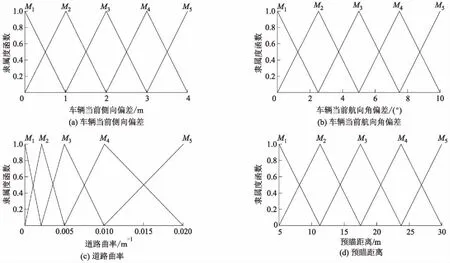
图4 不同输入参数的模糊隶属度函数
对于横向预瞄决策模块,模糊规则形式为
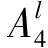
(5)
道路曲率的模糊隶属度划分与纵向预瞄决策模块相同.预瞄距离的变化范围为d∈(5,30)m,同样平均划分为5个模糊子集,如图4d所示.
将所构建的预瞄点决策模块与1.1节中的最优曲率预瞄驾驶员模型进行结合,构成如图5所示的仿人驾驶员模型.在驾驶过程中,预瞄点决策模块根据车路系统所提供的车辆状态(ev,eα,d)与道路信息(ρ), 为驾驶员模型决策预瞄距离d与侧向调整dl,通过最优曲率预瞄模型最终计算得到转向盘转角并完成对车辆的转向控制.由于预瞄决策的模糊规则量较大(5×5×5+5×5共150条),手工制定存在困难,为确保模型具有良好的仿人特性,需要借助实际驾驶员驾驶数据对模糊规则进行优化.
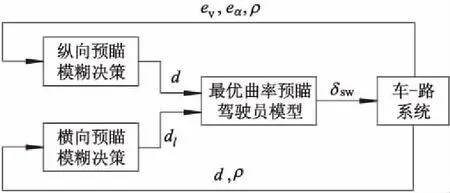
图5 仿人驾驶员模型
2 熟练驾驶员驾驶数据采集及分析
2.1 试验设备及试验场地
驾驶员的操纵特性最终反映为行驶轨迹,因此高精度的弯道行驶轨迹能够在一定程度上表征驾驶员的转向操纵特性.为保证车辆轨迹信息的精确性,采用图6所示的设备进行数据采集.试验车辆为斯柯达明锐汽车,其行驶轨迹由SDI-600GI型号的定位装置记录.该定位装置由全球卫星定位系统(global navigation satellite system,GNSS)与惯性导航系统(inertial navigation system,INS)组成,能够提供±0.01 m的定位精度.

图6 试验车辆及定位装置
试验场地如图7所示,驾驶员在1次弯道行驶时需要经过5个不同的路段,分别为直线路段、第1段定曲率弯道、过渡路段、第2段定曲率弯道与最终的直线路段.试验道路长度大于400 m.
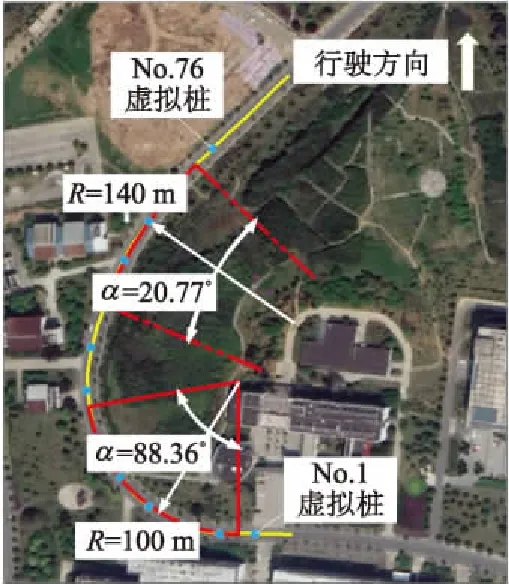
图7 试验场地
2.2 轨迹数据处理方法
试验采集的轨迹信息为20 Hz的时序GPS坐标序列.为了研究车辆位于不同试验路段时在车道上的侧向位置情况,在双车道的中心线上间隔4.24 m共设置了76个虚拟桩(如图7、8所示).通过计算车辆在经过各虚拟桩时,距当前车道中心线的距离,即可得到基于虚拟桩号更新的车辆侧向偏差序列,计算方法如图8所示.
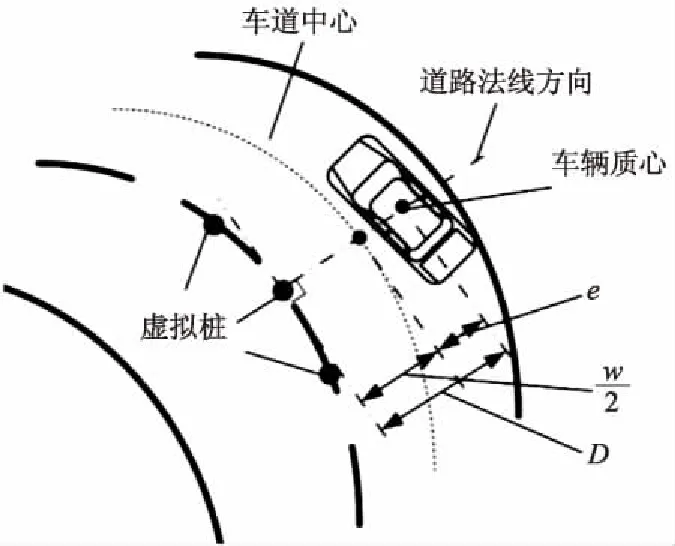
图8 虚拟桩处侧向偏差的计算
虚拟桩处的侧向偏差定义为在虚拟桩处车辆质心与车道中心在道路法线方向上的距离.因此,侧向偏差为
(6)
式中:w为路宽,w=3.2 m;D为车辆和虚拟桩的距离.
基于虚拟桩更新的车辆侧向偏差序列与时序的侧向偏差序列相比,能够有效避免不同次试验间车速偏差对于侧向偏差序列的影响,便于将多组试验的轨迹数据进行对比.
2.3 试验对象与试验过程
为避免在采集行驶数据时引入由于新手驾驶员误操作而产生的误差,试验对象定为5名驾校教练,即具有丰富驾驶经验的熟练驾驶员.这5名驾驶员相关信息如表1所示.
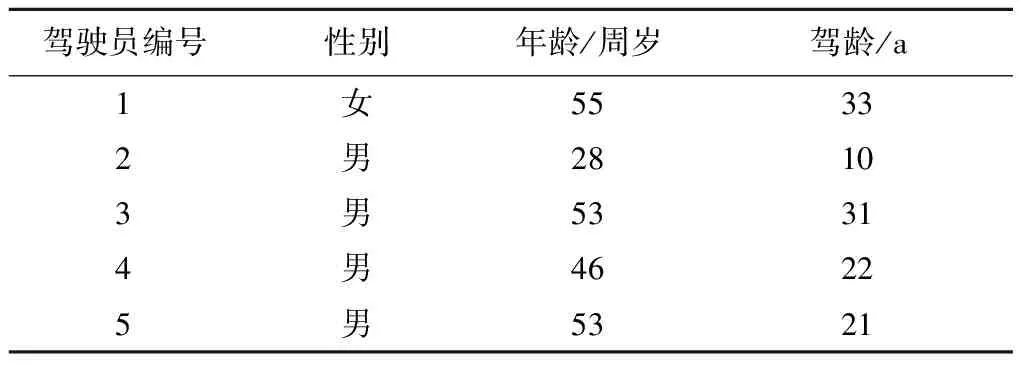
表1 熟练驾驶员相关信息
为忽略纵向速度控制对车辆转向控制的影响,每位驾驶员被要求以特定车速完成试验.试验场地留有足够的距离以保证驾驶员在到达第1个虚拟桩前达到指定车速.在每个特定车速下试验开始前,每位驾驶员都会进行1次额外的行驶来熟悉场地,该数据不会被记录.随后,每位驾驶员将会分别在4个指定车速(20、30、40、50 km·h-1)下各完成6次试验,试验次数总计为120次.
2.4 试验结果分析
汇总分析后的试验数据表明,在同一车速下,5名熟练驾驶员间具有相似的行驶轨迹.为表述这一特征,以车速为40 km·h-1下的行驶轨迹为例,采用各虚拟桩处侧向偏差的箱线图所组成的箱线图序列来表征熟练驾驶员们在行驶过程中的轨迹分布情况,如图9所示.各桩号处箱线图的箱须两端分别为该处侧向偏差去除异常值后的最大与最小值,箱体的上下边沿分别为轨迹分布的75百分位与25百分位,中部的短横线为50百分位.因此,熟练驾驶员在经过各虚拟桩时,50%的侧向偏差会集中在箱体所构成的区域内.
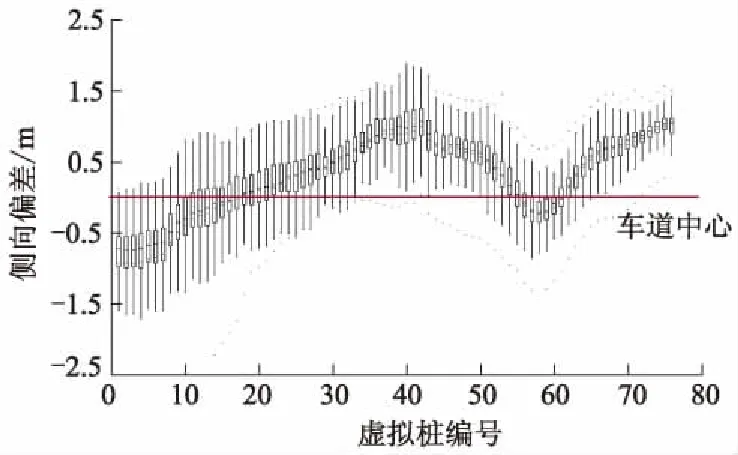
图9 车速为40 km·h-1时的轨迹分布
为使驾驶员模型具有较好的仿人特征,其行驶轨迹应尽可能通过熟练驾驶员的轨迹集中分布区域.为进一步明确优化目标,选取各虚拟桩处轨迹分布的50百分位值作为模型优化的目标轨迹,即图9箱体中短横线所组成的侧向偏差序列.驾驶员模型的轨迹越靠近目标轨迹,则越可能处于熟练驾驶员的轨迹集中分布区域,则被认为具有仿人驾驶特征.各目标车速下的目标轨迹如图10所示.
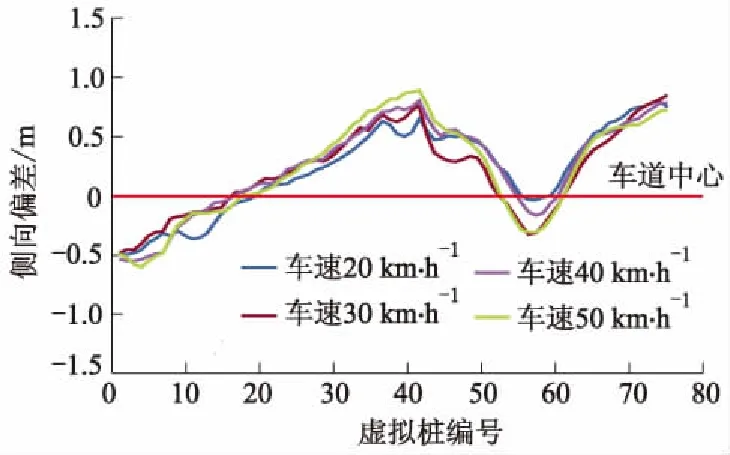
图10 不同车速下的目标轨迹
3 仿人驾驶员模型预瞄规则优化
3.1 蚁群算法优化模糊规则
第1节中所提出的仿人驾驶员模型应当在给定车速下与第2节分析得出的熟练驾驶员目标轨迹相似,而提升驾驶员模型轨迹仿人特性的关键在于横、纵向预瞄模糊决策规则的制定,其可以视为1个优化组合问题.蚁群算法(ant colony optimization,ACO)具有鲁棒性、并行性、正反馈等特性,其对优化组合问题的求解往往能够取得良好的结果[20-22].因此,以熟练驾驶员轨迹为目标,采用蚁群算法对仿人驾驶员模型中的横、纵向预瞄模糊决策规则进行优化.
在优化过程中,驾驶员模型轨迹与熟练驾驶员目标轨迹间的均方根误差(root mean square error,RMSE)被用于评价模型与熟练驾驶员之间的相似性或接近度,可根据下式进行计算:
(7)
式中:Xi为驾驶员模型轨迹在第i虚拟桩处的侧向偏差;Ti为目标轨迹在该处的侧向偏差.
为将蚁群算法应用于模糊规则的优化,构建如图11所示的节点空间.节点空间为m×n的矩阵,节点Pij代表在第j条模糊规则中选择第i模糊规则值,节点矩阵内部值为对应规则值的信息素浓度τij,反映了蚂蚁位于第j列模糊规则时选择第i个模糊规则值的可能性.对于本研究所提出的横、纵向预瞄决策模块对应的节点空间,n为150,其中前125列为纵向预瞄模块所对应的模糊规则,后25列为横向预瞄模块对应的模糊规则.m为5,其中对于纵向预瞄模块,节点从上到下所对应的模糊规则值为[5.00,11.75,18.50,25.25,30.00]m,对于横向预瞄模块,节点从上到下对应的模糊规则值为[-1.0,-0.5,0,0.5,1.0]m.当蚂蚁从第1列至第n列完成1次路径搜索后,即可获得1组完整的模糊规则.
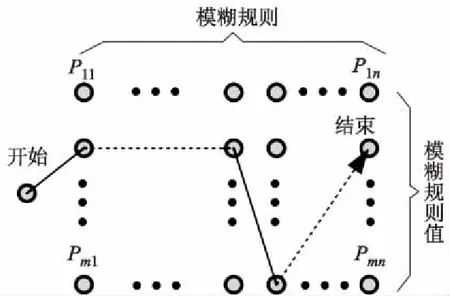
图11 蚁群算法路径搜索
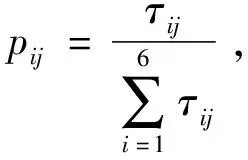
所有蚂蚁完成路径搜索后,按照式(8)对各节点处的信息素浓度进行更新.
(8)
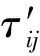
(9)
蚁群迭代次数选为200次,A=50个,k=0.7,信息素的初始值统一设为200.选取所有迭代过程中,RMSE最优的蚂蚁所代表的模糊规则作为最终仿人驾驶员模型的横、纵向预瞄规则.
3.2 仿真及结果分析
通过导入道路GPS信息与卫星地图,在PreScan中构建了与第2节实车试验相同的仿真环境,如图12所示,并在Simulink中完成第1节所述的驾驶员模型搭建.车辆动力学模型选用PreScan中提供的2自由度单车模型,整车质量为1 480 kg,长、宽、高分别为4 425、1 860、1 314 mm,轴距为2 700 mm,前、后轮距分别为1 585、1 580 mm,车辆质心至前、后轴距离分别为1 080、1 620 mm,x、y、z轴转动惯量分别为124、2 242、2 562 kg·m2,前、后轮胎刚度分别为62 191、98 727 N·rad-1.
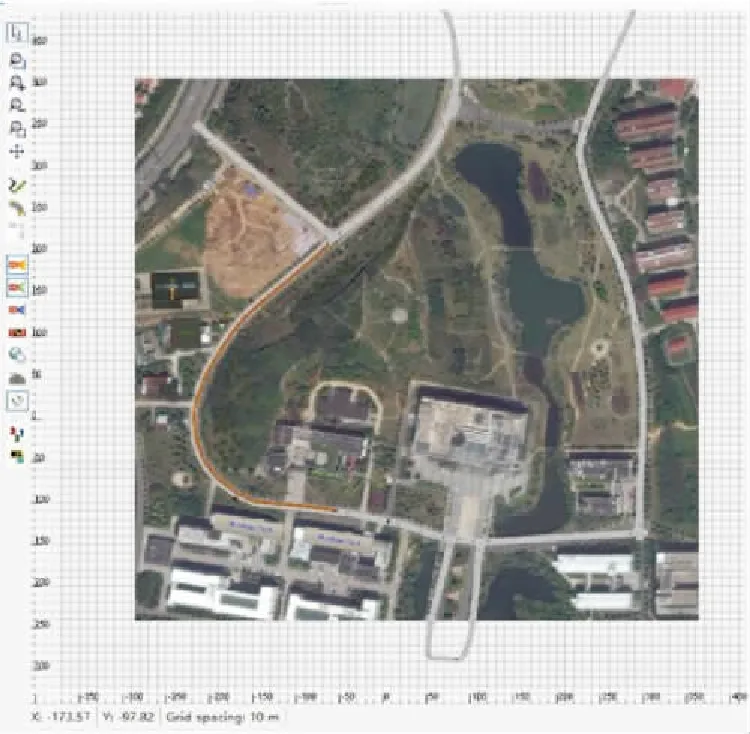
图12 基于PreScan仿真环境构建
车速为40 km·h-1时,经蚁群算法优化过后的仿人驾驶员模型与熟练驾驶员、最优曲率预瞄驾驶员模型轨迹对比如图13所示.其中,最优曲率预瞄驾驶员模型的预瞄距离为遍历所有可行预瞄距离后的最优值.由于熟练驾驶员目标轨迹为虚拟桩处的侧向偏差序列,为便于对比,假定虚拟桩间的侧向偏差为一定值,故轨迹呈阶梯状.为进一步说明预瞄点横、纵向自适应调节的必要性,图中还附加了同样采用蚁群算法优化的预瞄距离自适应(仅对预瞄点进行纵向调节)驾驶员模型轨迹.
从图13可看出:最优曲率预瞄驾驶员模型即使选取整体误差最小的预瞄时间,其轨迹与熟练驾驶员目标轨迹仍有较大区别.预瞄距离自适应驾驶员模型与固定预瞄距离的最优曲率预瞄模型相比,仿人程度有一定改善,但仍然不够理想,尤其是在距起始点行驶距离100 m至200 m的路段.本研究提出的仿人驾驶员转向控制模型,在经过蚁群算法优化后,与熟练驾驶员的行驶轨迹非常相似.以上各模型在不同车速下,与熟练驾驶员目标轨迹间的均方根误差如表2所示.仿真结果显示,仿人驾驶员转向控制模型在各个车速下,仿人程度均有较大提高.
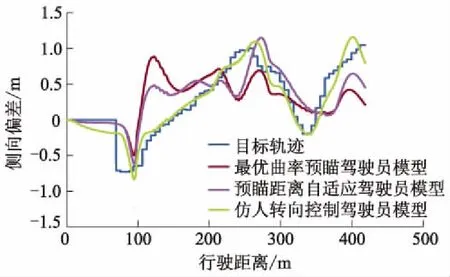
图13 车速为40 km·h-1时的轨迹对比
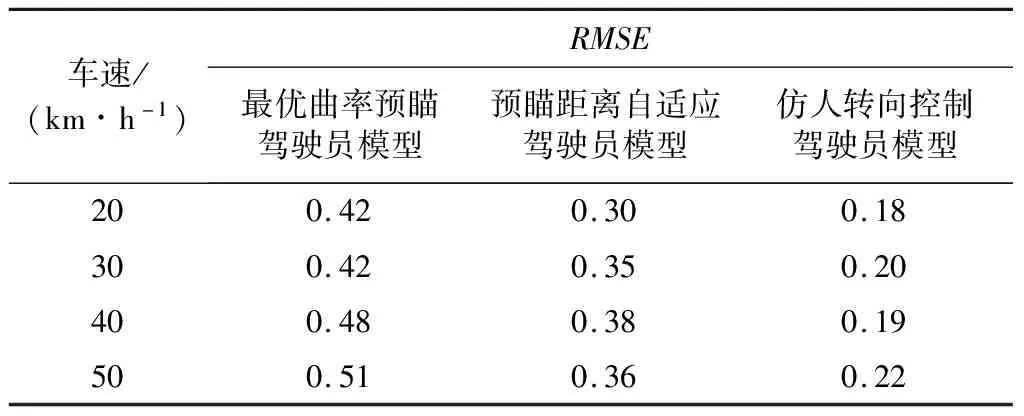
表2 不同车速下RMSE仿真结果 m
为进一步验证提出的仿人转向控制驾驶员模型与对应的优化方法在其他曲率弯道下的适用性,在PreScan中构建了如图14所示的连续多曲率弯道仿真场景,并基于驾驶模拟仪所采集到的熟练驾驶员驾驶轨迹对所提出的驾驶员模型的仿人转向特性进行验证.
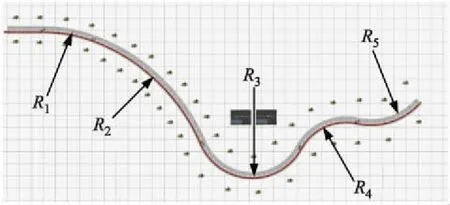
图14 多曲率弯道下的模型适应性验证
所构建的仿真道路共由5段不同曲率的弯道组成,其曲率半径R1、R2、R3、R4、R5分别为120、160、70、43、52 m;对应的弯道偏转角分别为20°、46°、128°、73°、61°,弯道全长384 m.由于存在曲率较大的弯道路段,仿真车速设定为30 km·h-1.驾驶员模型优化前,预先采集了1名熟练驾驶员在该弯道上的行驶轨迹,并将该轨迹作为模型优化的目标轨迹.运用蚁群算法迭代优化100次后,熟练驾驶员目标轨迹、最优曲率预瞄驾驶员模型轨迹与优化后的仿人转向控制驾驶员模型行驶轨迹如图15所示,由于缺乏预瞄点的自适应调节,最优曲率预瞄驾驶员模型与熟练驾驶员目标轨迹差距较大,RMSE为0.58 m.仿人转向控制驾驶员模型在经过优化后明显表现出与熟练驾驶员相似的行驶轨迹,RMSE为0.17 m,仿人转向特性有了显著提升;所提出的仿人转向控制驾驶员模型及优化方法能够适用于多种曲率的弯道驾驶场景.
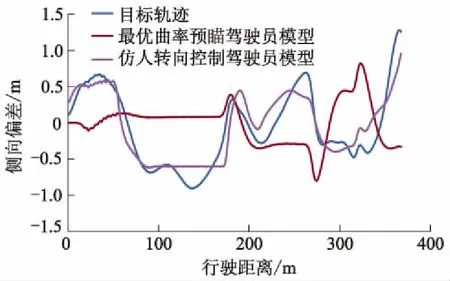
图15 多曲率弯道仿真结果
4 结 论
1)基于最优曲率预瞄驾驶员模型与T-S模糊推理系统,构建了模拟人类驾驶员预瞄点调节机制的预瞄点横、纵向自适应调节的仿人转向控制驾驶员模型.
2)采用蚁群算法,以熟练驾驶员行驶轨迹为目标,对仿人转向控制驾驶员模型中的模糊规则进行优化.优化后的仿人驾驶员模型的仿人程度比最优曲率预瞄驾驶员模型与预瞄距离自适应模型更好.
3)提出的仿人驾驶员转向控制模型在不同的定车速下均能较好地复现出熟练驾驶员的行驶轨迹,同时,提出的驾驶员模型与优化方法可以应用于不同曲率的弯道行驶.
