基于钢锭生产过程换热模型的工艺节能优化
2021-07-14黎涛涛苏福永温治
黎涛涛,苏福永,温治
(1.北京科技大学能源与环境工程学院,北京,100083;2.冶金工业节能减排北京市重点实验室,北京,100083)
近年来,随着钢铁企业的不断发展,钢锭入炉前的保温措施日益完善,钢锭入炉状态与生产工艺密切相关,因此加热工艺需要随着钢锭入炉状态而进行调整,达到节能减排的目的。钢锭入炉前需要先在模具中凝固,XU 等[1]研究了GCr15钢在断面上的凝固过程,并讨论该过程的影响因素;BERTELLI 等[2]开发反传热模型,在确定的冷却条件下,分析了铸件的热过程,避免由热引起的冶金缺陷;CAI等[3]采用EFG模型,求解连铸模具内部的传热问题,发现高热流区直接决定了初始坯壳的生长特性;李昊[4]通过ANSYS 软件模拟空心钢锭凝固过程温度场,确定合适的冷却介质及其换热系数;李龙[5]发现铸坯缓冷过程影响钢坯的表面裂纹的产生;ANSARIDEIFOLI 等[6]采用有限元模型研究了冷却速率对定向凝固炉中多晶硅锭最终组织的影响;SONG 等[7]研究了过热和冷却条件对凝固组织的影响,并改善凝固组织;YANG等[8]采用黏塑性有限元模型进行了热力学模拟,分析了钢锭凝固过程中的应力−应变演化;ZHANG等[9]提出了钢锭在不同凝固阶段的传热限制步骤;而GRESS 等[10]提出了通过求多准则全局极值,求解坯料最佳冷却温度和冷却速率的计算方法;AO等[11]建立了空心侧壁保温单向凝固温度场的数学模型,空心侧壁显著提高了保温效果,抑制了铸件定向凝固侧壁的传热。
钢锭在脱模后通常装入保温罩进行转运,曹先常等[12]研究了热锭保温运输,开发了钢锭保温运输的节能量计算方法;ZHANG 等[13]发现在坯料输送过程中加入保温罩,可有效提高粗轧前坯料的温度均匀性;SOMRIEWWONGKUL等[14]发现增加保温层厚度可以减少钢坯温度的不均匀性。
钢锭在进入均热炉后的换热情况也至关重要,宋小飞等[15]模拟了高温蓄热式均热炉内的流动和传热过程,得到了各工艺参数对钢锭与炉气间对流换热系数的影响规律;隋玲云[16]发现18CrNi3Mo钢的钢锭在均热炉内升温时间以及高温段停留时间对钢锭的影响较大;刘颖等[17]采用CFD 建立蓄热式加热炉内流动−燃烧−传热模型,并通过优化提高钢坯表面热流沿炉宽方向分布的均匀性;GARCÍA 等[18]采用CFD 模拟钢坯在加热炉内加热,并讨论恒定的铸坯发射率对模拟结果的影响;CHEN等[19]提出了一种钢坯加热炉的数值模型,包括钢坯四周热流计算和钢坯内部二维热传导计算;KHOUKIT 等[20]研究了钢坯在加热炉内表面热辐射作用下的温度分布,并采用有限体积法和高斯−塞德尔迭代法对二维稳态热传导方程进行数值求解;GUO 等[21]利用FORGE 软件模拟钢锭的加热过程,以钢锭脱模后的温度场作为加热过程的初始温度场,分析加热过程的温度场,制定了钢锭的加热规范;CHENG 等[22]采用电阻加热法在模具内直接加热坯料,实现热锻过程中的快速加热和逐步变形。因此,在钢锭的生产过程中进行工艺节能的同时也要兼顾热过程对产品性能的影响。
本文综合考虑了蓄热燃烧技术以及钢锭入炉前各阶段热过程对钢锭加热效果的影响,对钢锭系统热过程进行数值模拟,以此为理论基础指导现场的工艺调节。
1 钢锭生产过程换热模型
1.1 钢锭冷却过程数学模型
钢锭冷却过程是指钢锭从浇注结束到装入保温设备为止这一阶段。该阶段在建模时可分为模内冷却和模外冷却2 个部分,同时为减少计算量,对模型进行以下简化:
1)同批钢锭的脱模过程同时进行,忽略该过程的热损耗;
2)忽略各钢锭之间的影响;
3)钢锭的初温为浇注温度,锭模温度为烤模温度且分布均匀;
4)忽略钢锭端面散热的影响和纵向传热;
5)钢锭和铸模为各向同性;
6)传热方面将液态钢水的流动效果考虑到液相导热系数上;
7)相变过程的计算上采用等效热容法处理钢锭的凝固潜热。
1.1.1 钢锭冷却过程的分析
钢锭的冷却过程中,热过程较复杂。首先,在钢锭浇注完毕时,钢锭与锭模紧密相连,传热主要为热传导。随着钢锭在模内冷却,钢锭逐渐凝固,其体积会减小,因此在冷却一定时间后,钢锭与锭模之间将产生缝隙(实际中除了缝隙外,钢锭与锭模之间还有部分黏连),此时的热过程除了热传导外还有辐射换热和自然对流。在实际情况中,自然对流的影响非常小,因此在计算过程中忽略自然对流的影响。图1所示为钢锭在模内冷却和模外冷却过程中的热交换过程示意图。具体的热交换过程包括:

图1 钢锭在模内冷却和模外冷程中的热交换过程示意图Fig.1 Heat exchange process of steel ingot cooling in mould and cooling out mould
1)模内冷却:钢锭内部向表面的导热,钢锭表面与锭模内壁间的辐射换热及其有部分黏连时的导热,锭模内部的导热,锭模外表面与外部空间的辐射和对流换热;
2)模外冷却:钢锭内部的导热;钢锭外表面对外部空间辐射散热和对空气的对流散热。
1.1.2 控制方程及其定解条件
该阶段钢锭控制方程为

式中:ρ为密度,kg/m3;Cp为等压比热容,J/(kg·K);T为温度分布,K;τ为时刻,s;λ为导热系数,W/(m·K)。
模内冷却过程初始条件(τ=0时)为

式中:Ts(x,y)为钢锭的温度分布,K;Tm(x,y)为模内冷却时锭模的温度分布,K;Tm0为烤模温度,K;Ts0为浇铸温度,K。
边界条件为:
1)钢锭中心断面(按对称传热处理)
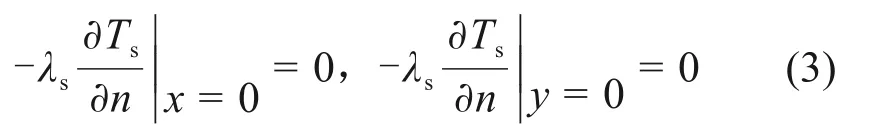
式中:λs为钢锭的导热系数,W/(m·K)。
2)锭模外表面

式中:λm为锭模的导热系数,W/(m·K);∂Ωm为锭模的外边界;εm为锭模的发射率;αm0为环境与锭模外表面的自然对流换热系数,W/(m2·K)。
3)钢锭外表面或模内表面

式中:∂Ωs为钢锭的外边界;∂Ω′m锭模区域的内边界;n为表面法向量;A为辐射换热所占的权重,介于0~1 之间;σ0为黑体辐射常数,取5.67×10−8W/(m2·K4);εs为钢锭发射率;λs为钢锭的导热系数,W/(m2·K);λsm为钢锭与锭模的接触部分的导热系数,W/(m2·K)。
模外冷却过程初始条件(τ=τ1时),为

式中:τ1为钢锭脱模时刻,s;Ts1为模内冷却结束时钢锭的温度分布,K。
边界条件为:
1)钢锭中心断面同式(3)。
2)钢锭外表面τ>τ1时,

式中:αs0为空气与锭模外表面的自然对流换热系数,W/(m2·K)。
1.2 钢锭保温过程数学模型
1.2.1 钢锭保温过程的分析
钢锭的保温过程是在保温设备中的热过程。保温设备内,钢锭不吸收外来热量,靠自身的热量均热。同时,保温罩使钢锭减少自身热量的散失以实现钢锭的热装热送。钢锭和保温设备的墙壁存在热交换,也和漏入的少量空气存在自然对流换热。图2所示为钢锭在保温设备内保温过程示意图,由图2可见:钢锭保温过程的主要热过程主要包含以下几个方面:钢锭内部向外表面导热、钢锭外表面和保温设备之间的辐射和对流换热、保温设备内部导热及其外表面与环境之间的辐射和对流换热。
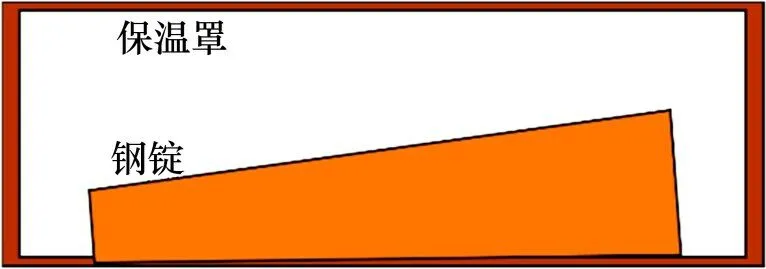
图2 钢锭在保温设备内保温过程示意图Fig.2 Schematic diagram of insulation process of steel ingot in insulation equipment
对钢锭的保温过程进行如下假设:
1)保温罩内钢锭性质完全相同;
2)保温罩在计算过程中只沿其壁厚方向存在温差;
3)保温罩的器壁各层材料之间接触良好;
4)保温罩内钢锭的外部传热条件是相同的。
1.2.2 控制方程及其定解条件
钢锭保温过程控制方程同式(1)。定解条件中初始条件(τ=τ2时),如下:

式中:τ2为钢锭装保温设备时刻,s;Ts2为模外冷却结束时钢锭的温度分布,K;Tb为保温时保温罩的温度分布,K;Tb0为模外冷却结束时保温罩的温度分布,K。
该过程的边界条件如下。
1)钢锭中心断面同式(2)。
2)钢锭外表面

式中:αsa为保温设备内漏入的空气与钢锭间的自然对流换热系数,W/(m2·K);φsb为钢锭与保温罩墙壁间的角系数;Ta为保温罩内空气温度分布,K。
3)保温墙壁内表面

式中:λb为保温罩墙壁的导热系数,W/(m·K);εb为保温墙壁的发射率;φbs为墙壁与钢锭间的角系数;αba为保温设备内漏入的空气和墙壁间的自然对流换热系数,W/(m2·K)。
4)保温墙壁外表面
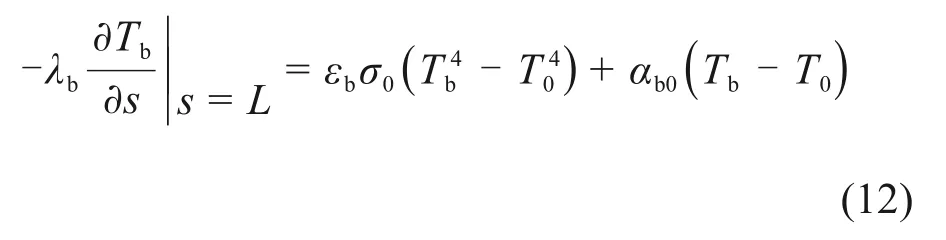
式中:αb0为保温罩外壁面与外部环境的自然对流换热系数,W/(m2·K)。
1.3 钢锭加热过程数学模型
1.3.1 钢锭加热过程的分析
钢锭的加热过程为钢锭入炉至钢锭出炉的过程。在该过程中,均热炉对钢锭进行加热使其符合初轧要求,这一过程是最重要的部分。图3所示为钢锭在均热炉内加热过程示意图。对该过程进行如下简化:

图3 钢锭在均热炉内加热过程示意图Fig.3 Schematic diagram of heating process of steel ingot in soaking pit
1)入炉的钢锭性质相同且温度均匀;
2)炉气为灰气体,其在炉内各处的温度、物性分布均匀;
3)炉墙、炉顶、炉底及钢锭表面均为灰表面;
4)钢锭表面加热条件相同;
5)均热炉所用燃料的发热量、温度和助燃空气温度等参数是定值。
1.3.2 控制方程及其定解条件
钢锭加热过程的控制方程如下。
1)钢锭内部导热方程
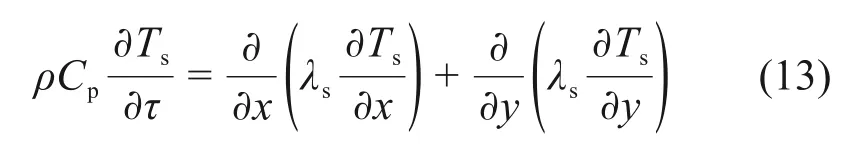
2)炉气温度控制方程

式中:Vf为炉气体积,m3;Cf为炉气比热容,J/(m3·K);Tf为炉气温度,K;Bf为燃料供入量,m3/s;QH为燃料的低发热量,J/m3;ηy为不完全燃烧系数;Cr为燃气比热容,J/(m3·K);Tr为燃气预热温度,K;n为空气过剩系数;L0为理论空气需要量,m3/m3;Cair为空气比热容,J/(m3·K);Tair为空气预热温度,K;Vn为燃烧产物生成量,m3/m3;Cy为烟气比热容,J/(m3·K);Ty为排烟温度,K;εf为炉气的发射率;φfs为炉气与钢锭间的角系数;Fs为钢锭换热表面积,m2;Hfs为炉气与钢锭间的对流换热系数,W/(m2·K);φfw为炉气与炉墙间的角系数;Fw为炉墙换热表面积,m2;Hfw为炉气与炉墙间的对流换热系数,W/(m2·K);Tw为炉墙的温度分布,K。
3)炉墙内部导热方程
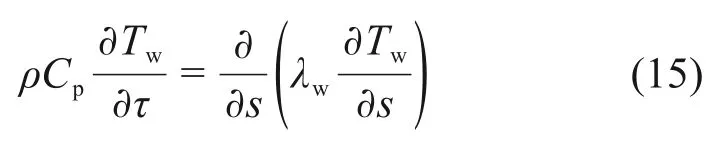
式中:λw为炉墙的导热系数,W/(m·K)。
4)烟气温度控制方程
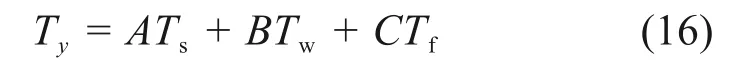
式中:A,B和C均为加权系数,且满足A+B+C=1。
该过程的初始条件(τ=τ3时),为

式中:τ3为钢锭入炉时刻,s;Ts3为保温过程结束时钢锭的温度分布,K。
边界条件如下。
1)钢锭外表面,当τ>τ3时:

式中:φsf为钢锭与炉气间角系数;φsw为钢锭与炉墙之间角系数。
2)炉墙内表面
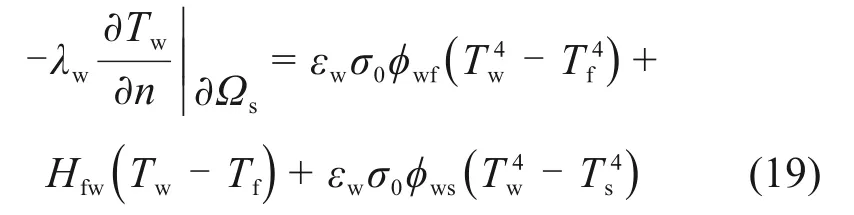
式中:∂Ω′w1为炉墙内表面;εw为炉墙的发射率;φwf为炉墙与炉气间角系数;φws为炉墙与钢锭之间角系数。
3)外表面
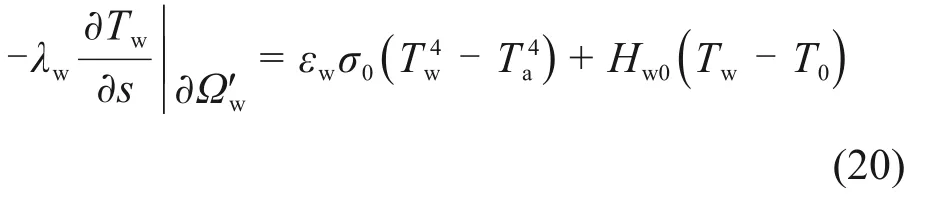
式中:∂Ω′w为炉墙外表面;Hw0为炉墙与环境的对流换热系数,W/(m2·K)。
1.4 钢锭系统热过程数学模型的数值求解
对所建立的钢锭生产过程换热数学模型采用交替隐式差分格式进行离散,并运用追赶法(TDMA)求解。在网格划分上,钢锭和锭模的网格尺寸,网格数量均不相同,为计算方便将求解区域分成4块,分别进行隐式求解,一块计算区域计算完毕后将成为另一计算区域的边界条件,以此迭代,完成对整个计算区域的求解。
2 模型验证
2.1 冷却过程数学模型
采用典型点温度跟踪法,每隔一定时间测量一次钢锭或锭模典型点的温度作为数学模型的验证对比点。在进行实验验证前,模型根据历史生产数据进行调试。本次验证以钢锭1/2高度的横界面为研究对象,采用二维交替隐式TDMA 法进行数值模拟计算,并将各典型点的计算结果与实测数据进行对比分析,统计其绝对误差和相对误差。现场均采用校准后的红外高温计进行测量,并取平均值。
测试工况下模内冷却时间为210 min,模外冷却时间50 min,普通加热法程序计算参数依照实际生产设定。由于钢锭在模内冷却过程中,钢锭表面温度无法测得,故测试了锭模外表面温度,并将外表面温度与程序计算值进行比较,计算结果如图4所示。当钢锭芯部全部凝结完毕后,钢锭通过脱模过程进入模外冷却过程。
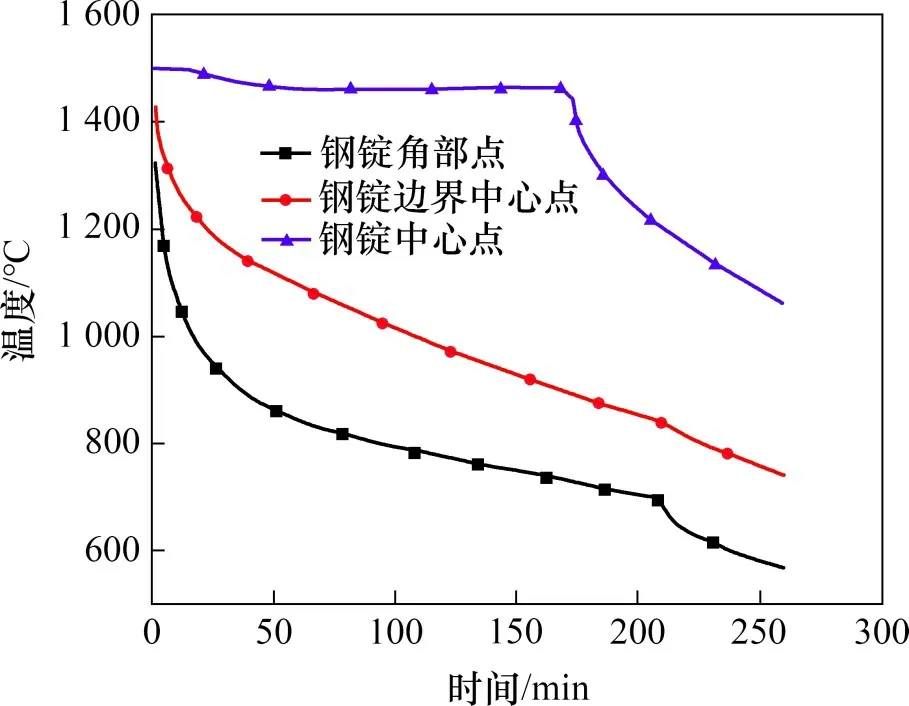
图4 钢锭冷却过程典型点温度计算值Fig.4 Calculation value of typical point temperature during ingot cooling
图5所示为钢锭冷却过程锭模典型点温度计算值与实测值对比。由图5可见:在模内冷却过程中,锭模边界中心点及角部点温度的计算值与实测值最大相对误差为2.1%,在模外冷却过程中,钢锭边界中心点及角部点温度的计算值与实测值最大相对误差为2.6%,符合计算准确度要求。

图5 钢锭冷却过程锭模典型点温度计算值与实测值对比图Fig.5 Comparison of calculated and measured values of typical temperature of ingot mold during cooling process
2.2 保温过程数学模型
由于保温罩与钢锭并不直接接触,直接测量保温罩表面温度很难真实反映钢锭温度变化,因此,掀开保温罩直接测量钢锭表面温度。为减少对保温过程的影响,对保温过程的典型时刻进行测量,并与计算值进行对比,如表1所示。从表1可见:边界中心点温度模拟值与实测值的最大相对误差为2.9%,钢锭保温过程数学模型准确性得到验证。

表1 钢锭保温过程典型点温度测量值与计算值Table 1 Temperature measured and calculated values at typical points in process of steel ingot insulation
2.3 加热过程数学模型
在炉内加热及保温过程温度验证方面,选取典型时刻,将实际测量值与模拟值对比,验证本计算模型的准确性,对比数据如表2所示。从表2可见:程序计算所需加热时间与实际生产所需加热时间基本吻合,且经过保温期后,在相同在炉时间情况下,钢锭出炉温度基本吻合。本模块计算最大相对误差为3.9%,本模块计算准确性得到验证。

表2 普通加热法模型试算与实测对比结果Table 2 Comparison between trial calculation and measurement results of general heating method model
3 生产过程节能优化
为进一步优化现场加热工艺,实现节能减排,运用所建立的数学模型对现有的110号和210 号加热工艺进行了模拟计算,并依据计算结果提出了优化措施。根据相关要求,钢锭出炉标准的断面温差控制在120~150 ℃/m。
3.1 110号加热工艺
表3所示为110 号加热工艺参数以及优化后的参数。以表3中参数分别模拟优化前后的加热工艺。图6所示为110号加热法优化前模拟结果。由图6可见:原加热工艺下,钢锭出炉时断面温差为61 ℃,高于轧制要求,存在优化空间,而优化后的加热工艺,钢锭出炉时断面温差为64 ℃,同样满足轧制要求,证明了本次优化是可行的。
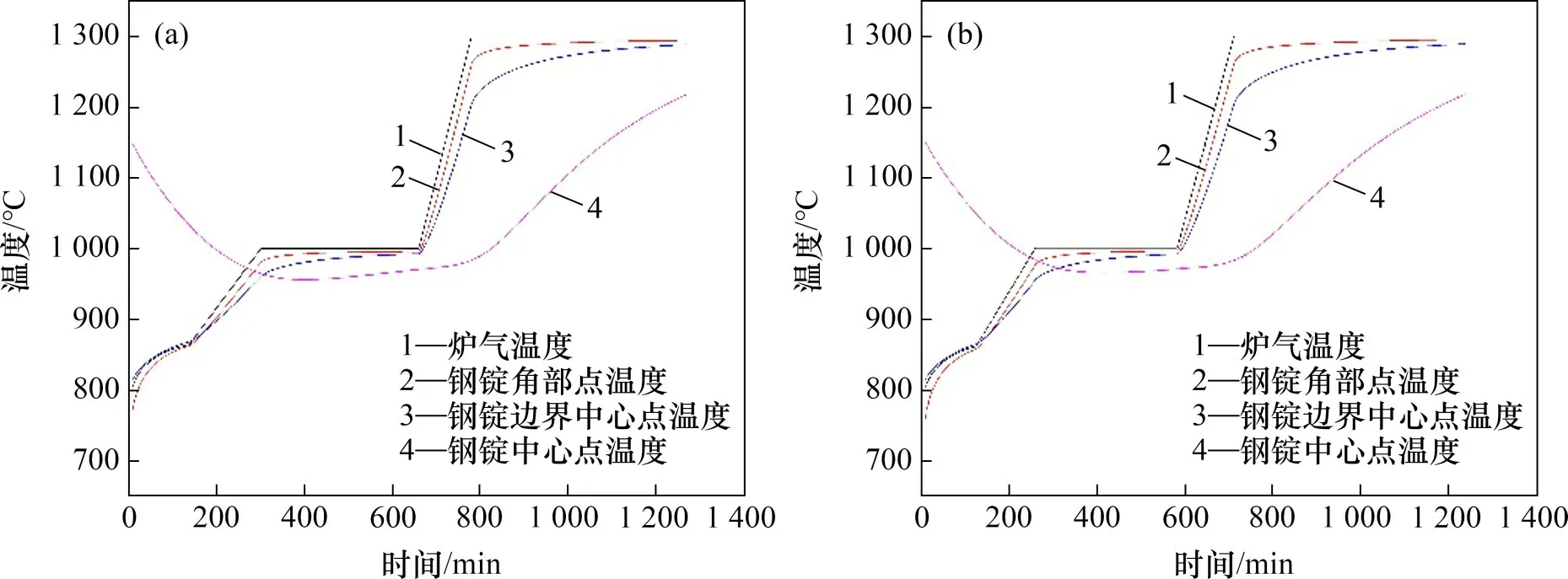
图6 110号加热工艺优化前后模拟结果Fig.6 Simulation results of No.110 heating method before and after optimization
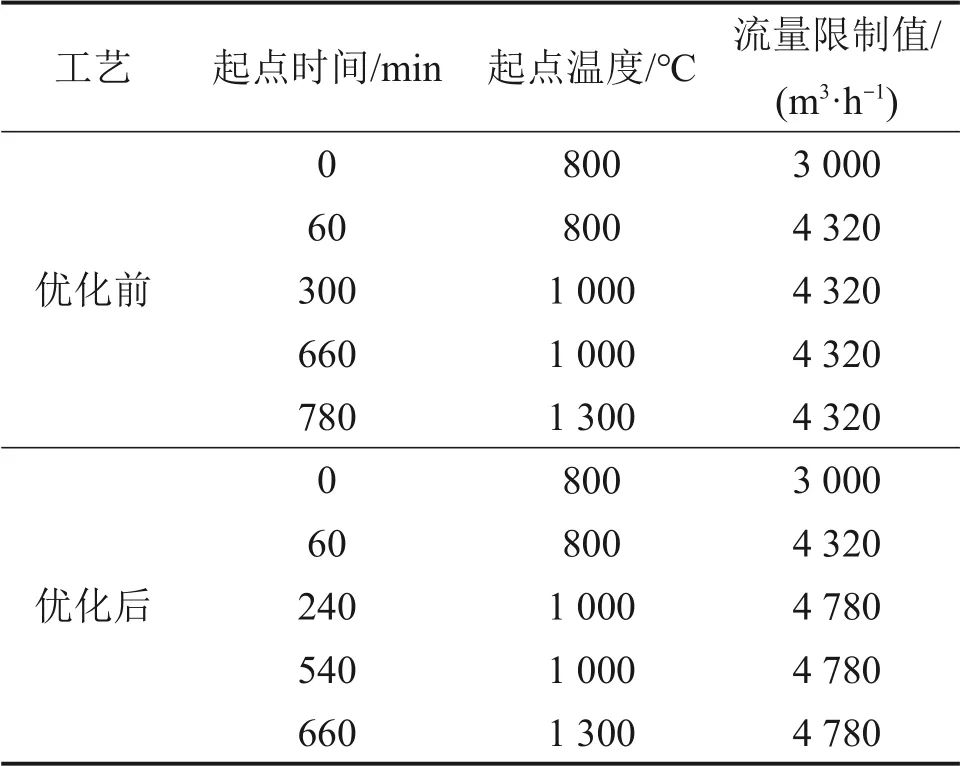
表3 110号加热工艺优化前后操作参数Table 3 Operation parameters before and after optimization of No.110 heating process
将优化后的加热工艺应用于实际生产后,110号加热工艺平均总煤气消耗量由16 848 m3减少到15 108 m3,平均节能率为10.3%,因此,对110 号加热法优化的节能效果显著。
3.2 210号加热法的优化
表4所示为210号加热工艺参数以及优化后的参数。采用表4中参数分别模拟计算了优化前后的加热工艺。图7所示为210号加热法优化前模拟结果。由图7可见:原加热工艺下,钢锭出炉时断面温差为45 ℃,高于轧制要求,且各加热保温段均有优化空间,而优化后的加热工艺,钢锭出炉时断面温差为48 ℃,同样满足轧制要求,证明了本次优化是可行的。
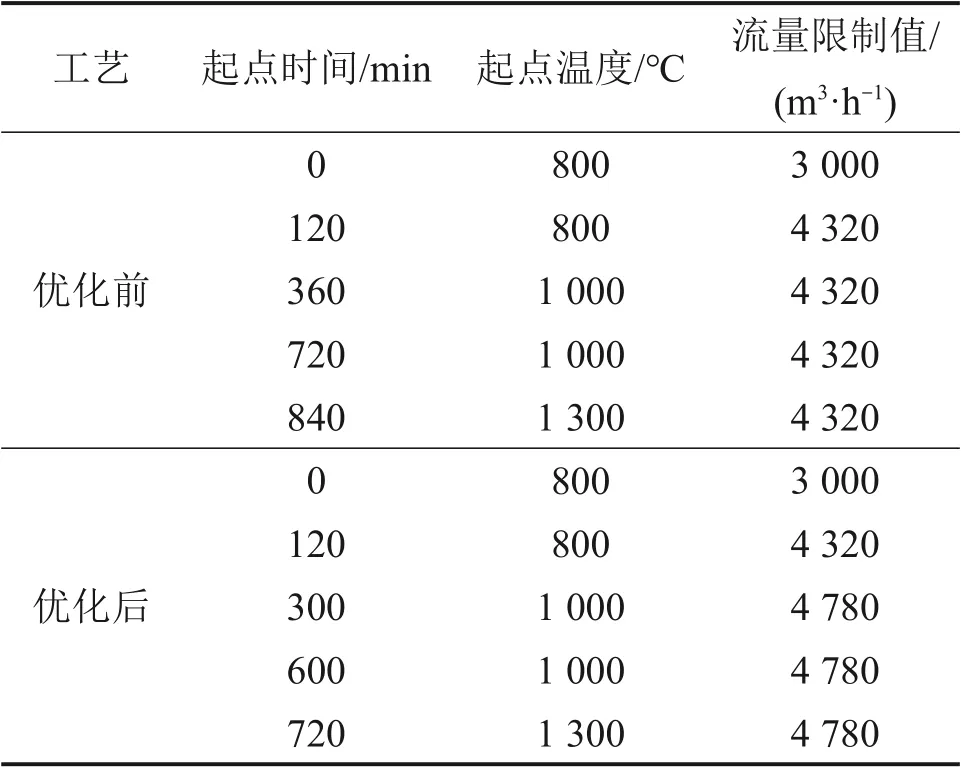
表4 210号加热工艺优化前后操作参数Table 4 Operation parameters before and after optimization of No.210 heating process

图7 210号加热法优化前后模拟结果Fig.7 Simulation results of No.210 heating method before and after optimization
将优化后的加热工艺应用于实际生产后,210号加热工艺平均总煤气消耗量由22 689 m3减少到21 268 m3,平均节能率为6.3%,因此,对210 号加热法优化的节能效果显著。
4 结论
1)采用温度跟踪法对“模内冷却模型”“模外冷却模型”“保温模型”“蓄热体换热模型”以及“钢锭加热模型”进行实测验证,对比模内冷却过程、模外冷却过程和保温过程模型计算值与实测值最大相对误差分别为2.1%,2.6%和2.9%,均在工程要求的允许范围内。
2)针对现有的110号及210号加热法提出了相应的节能优化方案,对110 号和210 号加热法进行优化后,在加热钢锭过程中,平均节能率分别为10.3%和6.3%,均热炉节能效果显著。
