榆树沟台钻孔应变受水位影响分析①

斯 琴， 关冬晓， 郭春生

(新疆维吾尔自治区地震局，新疆 乌鲁木齐 830011)

分量式钻孔应变观测是观测地形变和地应变的一种重要手段，用于研究地球物理过程和地球动力学过程的动态变化[1]。该仪器一般安装在钻孔中，使用特种水泥作为耦合介质，数据观测精度和稳定性都比较高，可以清晰地记录到固体潮汐变化和地震孕育过程中地壳的伸缩变形，适用于观测地应变和固体潮汐变化，为进一步研究地震孕育过程中的地应变变化规律提供了可靠数据，也为地球弹性研究提供了重要的参数指标[2]。因钻孔应变仪具有较高的观测灵敏度，所以其应变观测值也易受到环境干扰因素的影响，尤其是水位，对观测值的影响最大[3-4]。目前，关于水位变化对应变资料的影响，前人也做了很多研究。李广科等[5]整理重庆库区多套钻孔应变仪观测资料，对水位、气压与钻孔应变的关系进行了分析研究；张磊等[6]用地下水位变化获取与地下水抽取有关的信息，研究抽水对洞体应变仪影响，并建立相应的变化模型，对疑似场地环境干扰的数据进行验证；李兴坚[7]、刘川琴[8]等通过对连续多年的水位、应变观测数据进行跟踪分析，发现水位上升会引起应变值的下降变化(压应力增加)，两者呈同步变化。在做数据跟踪分析时，常会遇到如下情况，如水位变化的同时应变值也发生了大幅快速变化，就无法准确地判断应变值发生变化的原因是受水位影响？还是前兆异常？还是两者都有。所以定量分析水位变化对应变观测影响，并建立关系模型，对应变异常判定有很大的帮助，也有利于辅助检验异常的可信度。为了研究榆树沟台钻孔应变受地下水位的影响，本文中通过量化分析建立水位与应变两者的关系模型，为应变在水位影响时段的应变量变化幅度预测变化区间，从而为应变数据异常(水位变化时段)的判定提供量化依据。

1 台站基本情况

榆树沟台位于乌鲁木齐市东部山区，地质构造属于博格达弧型构造的西翼，北部400 m外为山前第一排呈北东走向的向斜构造，以三叠系泥岩、砂岩形成较为开阔平缓的浅山丘陵地貌[9]。山洞开凿在二叠系地层构成的中高山区，山洞完全凿建于二叠系岩层中，岩层走向60°，倾向325°，倾角70°。二叠纪岩层主要由黑灰色的油页岩、页岩、板岩和灰质砂岩层排列构成，由于岩性的抗风化差异，页岩被侵蚀成低地和沟壑，形成突兀的岩墙和陡崖地貌。山洞范围无断层构造，覆岩层厚约20～100 m。山洞旁为水流冲积的河谷，该河谷常年流水，但水流较小。榆树沟台分量钻孔应变仪观测井位于榆树沟山洞内，钻孔孔深34 m，孔径133 m，应变测量探头位于钻孔底部约31.25～33 m处，所在岩石岩性为泥岩和粉砂岩[10]。辅助测量探头安装在同一个钻孔内，温度探头安装深度约井下20 m，水位、气压探头安装深度约井下18.45 m。该台应变仪为RZB-2型四分量钻孔应变仪，采用圆筒式结构，圆筒内安置有应变探头。应变探头由4个依次呈45°的径向位移传感器组成，1#元件的方位角是N49°E。

2 应变与水位变化特征分析

地下水和应力、应变观测研究认为，水位的变化与含水岩体的应力—应变状态变化密切相关[11-13]。整理榆树沟台2015年1月1日～2018年6月30日的分量钻孔应变和水位的日均值数据(图1)，在每年的春季 2～4月，榆树沟分量应变因受春季融雪影响，应变数据呈现先压缩后拉张的明显变化，同期水位数据也出现先上升后下降的变化，两者变化形态比较一致，表现出较好的同步性和规律性，大体呈负相关变化。图1表明，融雪时段，榆树沟台分量钻孔应变对水位变化比较敏感，尤其是NS向、NW向和EW向表现比较突出，而NE向变化不明显，对水位的响应没有其他3个分量那么敏感。

根据每年融雪时段，榆树沟台分量钻孔应变快速压缩变化与钻孔水位加速上升变化表现出很好的同步性变化的特点。本文中采用最小二乘回归分析法研究钻孔应变与水位之间的关系，建立钻孔应变变化量与水位变化量之间的关系模型，并通过检验对该模型进行显著性检验，给出水位变化量对应变变化量的影响程度，最后为应变量在水位影响时段的变化幅度预测理论变化区间，以期为应变数据异常(水位变化时段)的判定提供量化依据。

3 数据处理方法

3.1 最小二乘回归分析

对于给定数据点(xi,yi)，i=1,2,…,n,满足如下关系，

yi=β0+β1xi+εi

. (1)

其最小二乘回归直线,

(2)

令

. (3)

则有

(4)

方差σ2的无偏估计

(5)

相关系数

(6)

3.2 t检验方法

t检验用于回归系数的显著性检验，即检验因变量y对自变量x的影响程度是否显著[15]。

如果变量x对y没有影响和解释作用,那么上面求解出的线性回归方程是没有意义的。因此对回归模型的显著性进行检验，也就是对x的变化是否影响到y进行检验，非常必要。

假设H0：β1=0,H1：β1≠0,当H0成立时，构建T统计量,

(7)

给定显著性水平α，记t为统计量(7)的观测值，若

(8)

则拒绝H0:β1=0，即认为自变量x对因变量y有显著性影响。

给定显著性水平α，在x=x0处，

(9)

4 数据计算及结果分析

4.1 建立回归模型

每年融雪时段，由于榆树沟台分量钻孔应变快速压缩变化与钻孔水位加速上升变化表现出很好的同步性，本文中统计了2015～2018年春季融雪时段水位开始出现大幅上升变化至水位达到最高值时的水位变化量和各分量开始出现压缩变化至压缩变化结束对应的应变观测的变化量(表1～6)。

根据表1～5可以得到榆树沟分量应变各分量的应变变化量与水位变化量的对应关系(表6)。表6中xi与yNSi、yEWi、yNEi、yNWi分别为研究钻孔水位变化量与分量应变NS向、EW向、NE向、NW向应变变化关系的样本点(图2)，4组数据的相关系数分别为0.958 3、0.993 4、0.661 4、 0.986 9，可看出榆树沟台钻孔水位变化量与榆树沟台分量应变变化量相关性比较高。

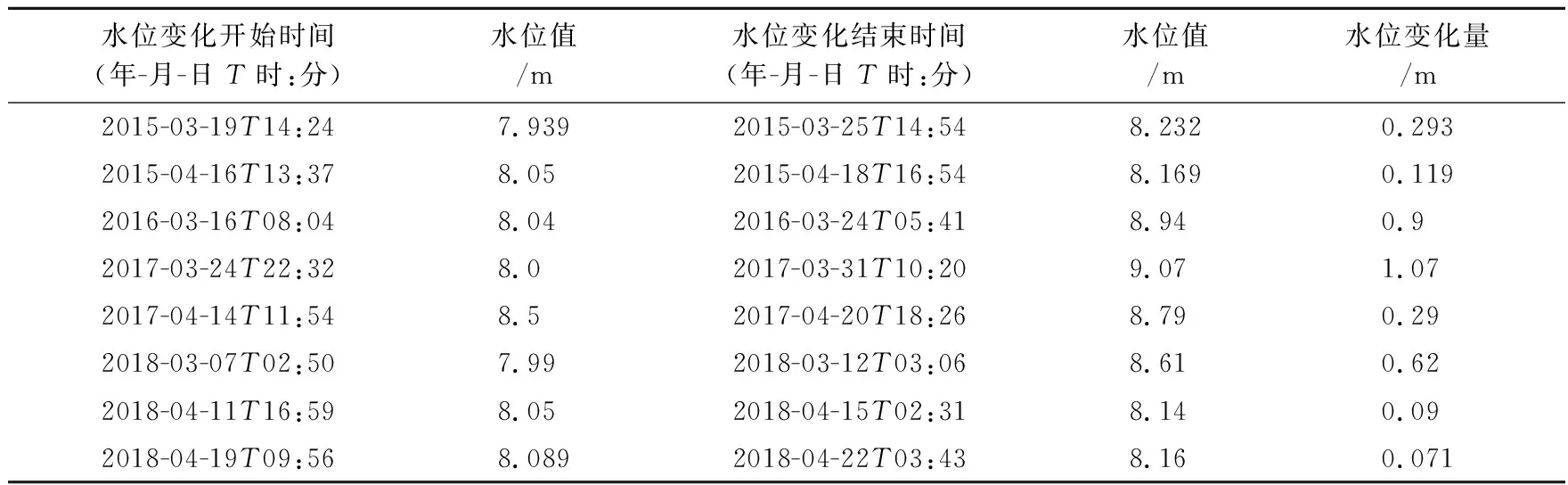
表1 榆树沟钻孔水位变化表

由表6，利用2.1中的最小二乘线性回归分析方法，根据式(2～6)计算得到最小二乘回归直线相关参数及每一组的相关系数(表7)。

表2 榆树沟钻孔应变NS向应变的变化表

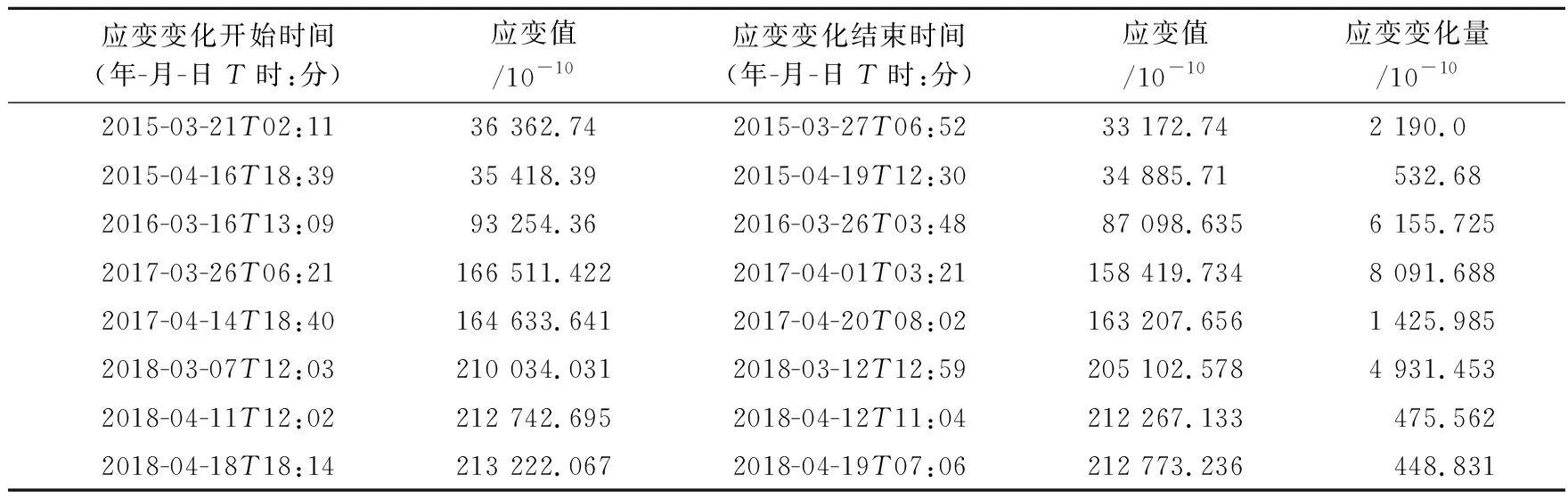
表3 榆树沟钻孔应变EW向应变的变化表

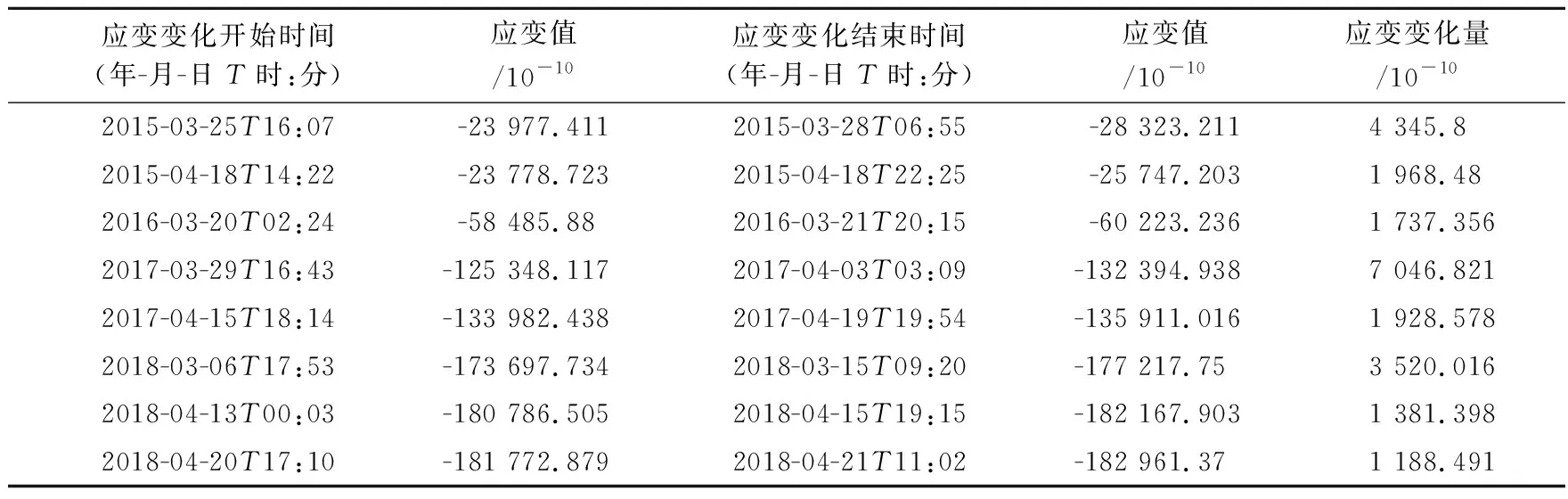
表4 榆树沟钻孔应变NE向应变的变化表

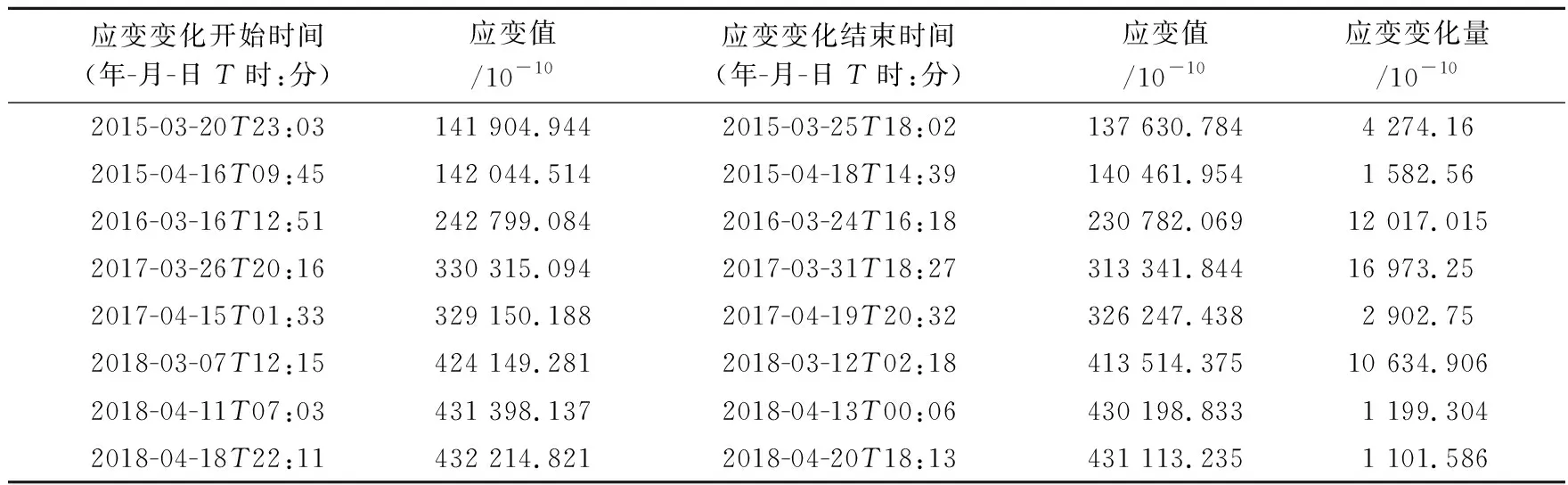
表5 榆树沟钻孔应变NW向应变的变化表

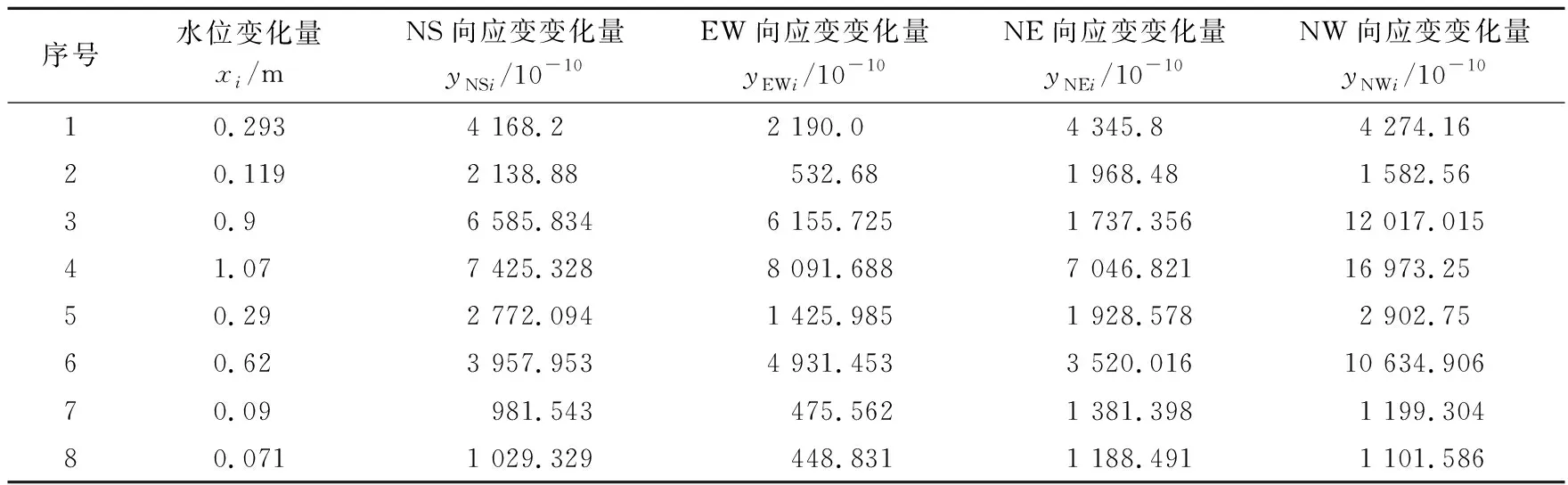
表6 榆树沟钻孔应变和水位变化量对应关系表

表7 最小二乘线性回归结果参数表

由表7可以计算得到榆树沟台钻孔水位变化量与分量钻孔应变NS向、EW向、NE向、NW向应变变化量之间的最小二乘回归直线方程，

(10)

相应的上式方差的无偏估计,

(11)

4.2 回归模型显著性检验

最后利用t检验方法对得到的回归模型(式10)进行显著性检验，依据式(7～8)分别用|tNS|、|tEW|、|tNE|和|tNW|表示回归模型式(10)中的4条直线t的统计量的观测值。假设：H0:β1=0,H1:β1≠0,有n=8，当H0成立时，(1) 对于给定显著性水平α=0.05，t0.025(n-2)=t0.025(6)=2.447，t统计量的观测值|tNS|=8.2162、|tEW|=21.131、|tNS|=15.017均大于t0.025(6)， 则拒绝H0，认为自变量x对因变量yNS、yEW、yNW有显著影响，即水位变化对分量应变NS向、EW向和NW向的应变变化影响显著，置信水平达到了95%。(2) 对于水位变化量与NE向应变变化量的回归直线，给定显著性水平α=0.05，t0.025(n-2)=t0.025(6)=2.447，t统计量的观测值|tNE|=2.159 8t0.025(6)，则在给定的显著性水平α=0.1条件下，自变量x对因变量yNEi有显著影响，即水位变化对分量钻孔应变NE向的应变变化影响显著，置信水平达到了90%。

上述检验结果表明，钻孔水位变化对分量钻孔应变变化影响显著，并且应变变化量和水位变化量的回归直线方程NS向、EW向和NW向的置信水平明显高于NE向，这与实际观测中分量应变NW向对水位变化的响应不是很敏感这一实测结果比较一致。

4.3 应变量变化区间分析

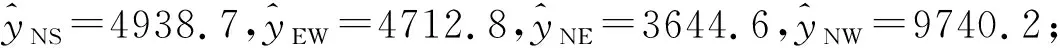
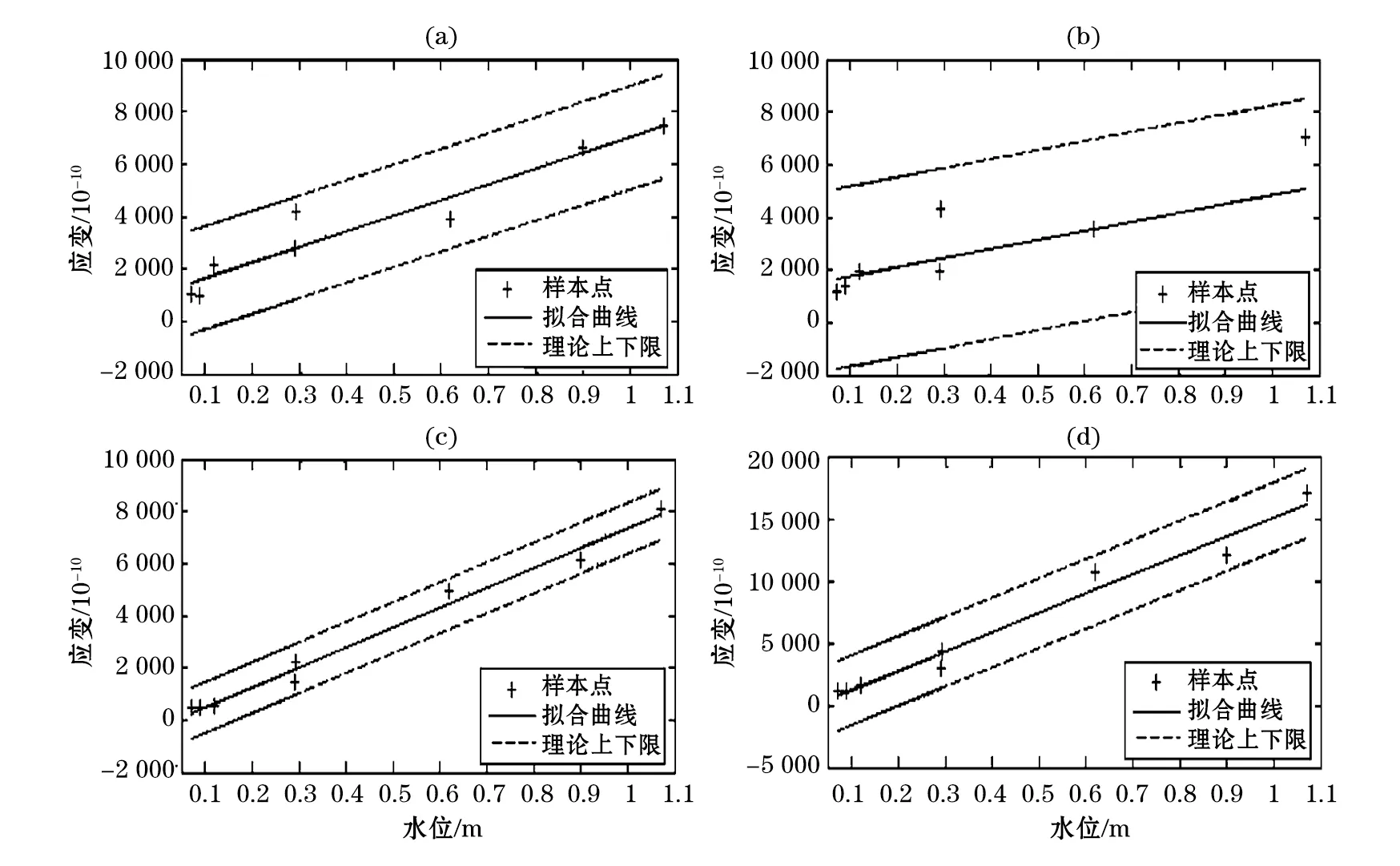
图2 榆树沟分量钻孔应变变化量与水位变化量线性拟合分析结果图(a) NS向 (b) EW向 (c) NE向 (d) NW向Fig.2 Linear fitting results of component borehole strain variation and water level variation in Yushugou station

5 结语

榆树沟台分量钻孔应变观测受春季融雪干扰影响显著，每年年初受春季融雪影响4个分量会表现出不同程度的加速压缩变化。在春季融雪时段，水位加速上升与应变加速压缩变化在时间上具有很好的同步性。统计2015～2018年春季融雪时段水位开始出现大幅上升变化至水位达到最高值时的水位变化量和各分量开始出现压缩变化至压缩变化结束对应的应变的变化量，采用最小二乘回归分析法得出榆树沟台分量钻孔应变变化量与水位变化量之间的回归方程，二者为正相关，即分量钻孔应变受水位影响的程度随着水位变化量的增大而增大。通过回归方程(式10)可以得到任意水位变化量x0对应的应变变化量y0的理论变化区间(图2虚线以内)，这一理论变化区间可以用于辅助判定在水位影响(融雪)时段钻孔应变也出现加速压缩变化的异常信度。得到的回归模型显示榆树沟分量钻孔应变变化在春季融雪时段受水位变化影响显著，可以利用钻孔水位做为辅助资料研究钻孔应变受水位影响的变化幅度。随着观测资料的积累，样本量的逐渐增加，可以对回归模型进行进一步修正和验证。