基于改进A*算法的药房机器人路径规划
2021-07-14姚善化
王 月, 姚善化
(安徽理工大学 电气与信息工程学院, 安徽 淮南 232000)
随着各大医院逐渐引入自动化药房系统,传统的人工取药工作被取药机器人所替代,取药机器人路径规划一直是研究的重点。路径规划算法主要包括Floyd算法[1]、人工势场法、蚁群算法[2]、RRT算法[3]等。A*算法[4]计算量小、路径规划搜索效率高,一直被广泛的研究。传统A*算法在进行路径规划过程中忽略了路径的搜索效率、安全性、平滑度。针对这些问题,很多学者对A*算法进行了改进。文献[5]为了提高路径搜索效率,引入跳点搜索法,但忽视了一些关键点,导致路径平滑度不高;文献[6]针对复杂路况下的路径规划问题,引入二次路径规划对路径进行优化,提升了路径规划效率,但忽略了与障碍物之间的安全间距问题;文献[7]引入扩展A*邻域法来扩大搜索方向,可以寻得一条更优的路径,但计算量增大,降低了A*算法搜索效率;文献[8]为了减少路径搜索的空间,对修改后的估计路径进行加权处理,但忽略了与障碍物之间的安全间距问题。
针对上述存在的问题,提出一种改进A*算法的药房机器人路径规划。首先,根据自动化药房的实际环境,搭建带有起始点、目标点和障碍物信息的栅格地图;其次,在已搭建好的地图上使用有向图法来预防各取药机器人间的碰撞问题;再次,对药房中的药架(在机器人进行路径规划时,将其当做障碍物)进行膨胀处理;最后,为了使路径搜索效率更高、平滑性更好,改进A*算法的评价函数结合几何法和平滑的圆弧来去除多余节点,得到光滑路径。本文所提出的改进A*算法可以优化移动机器人在路径搜索中的平滑度和安全性,同时搜索效率也显著得到提高。
1 自动化药房环境模型建立
采用栅格法搭建自动化药房的模型如图1所示。图1表示一个N*M大小的栅格地图(其中N=20,M=20)。对搭建好的地图进行定义:图中白色栅格为可行驶区域(代表这里无障碍物),反之为不可行驶区域。

图1 栅格地图
根据自动化药房环境采用栅格法对机器人运行环境进行地图建模。针对多机器人在作业过程中会产生相互碰撞的问题,采用双向图法对道路方向进行约束,规定货架间的道路为单行道,每个移动机器人只能在指定的取药空间内活动,且机器人把药物送到取药柜台后只能原路返回,这样可以避免机器人发生迎面碰撞的问题。约束机器人只能在规定的区域内作业,且作业完之后只能原路返回,这样可以避免移动机器人在作业过程中发生赶超碰撞、交叉碰撞的问题。对机器人行驶路线做以下规定:
(1) 每一条边为单行道,且规定机器人能双向行驶(即机器人在规定的取药空间内活动,并在送完药之后只能原路返回);
(2) 各机器人单次只可完成一个任务;
(3) 各机器人以2 m/s匀速行驶。
2 A*算法
2.1 传统A*算法
A*算法作为静态全局路径寻优的标准算法,主要在于估计成本h(x,y)的选取。A*算法的原理是:自规划路径的起始点开始,根据节点的扩展方向,不停地历遍栅格地图,旨在找到一条到目标点最优的搜索方向[9]。A*算法的评价函数为
f(x,y)=g(x,y)+h(x,y)
(1)
路径搜索对估计成本的选取有较高的要求,为了使选择的估计函数实用性和效率高,尽量使选择的估计代价值和实际代价值保持一致。A*算法的估计成本通常有两种表达形式:欧式距离和曼哈顿距离。
欧式距离的计算公式:
(2)
曼哈顿距离的计算公式:
h(x,y)Manhattan=|xn-xd|+|yn-yd|
(3)
其中:(xn,yn)为当前节点(x,y)的坐标;(xd,yd)为目标节点d的坐标。
A*算法在扩展节点时,会遍历周围所有栅格,如图2所示。考虑到在实际自动化药房环境中,机器人驶向特征为正向行驶(正南、正北、正东、正西),选择4个方向的扩展节点,如图3所示。基于这方面的考虑,选择两点间的曼哈顿距离作为估计函数效率更高[10]。

图2 传统A*节点扩展图 图3 改进A*节点扩展图
2.2 改进A*算法
2.2.1 障碍物膨胀处理
传统A*算法在进行路径规划时,考虑的质点问题是机器人本体,像机器人的长、宽、高等外部特征没有考虑在内。但自动化药房中存在很多排药架,药架上也摆满了药物,取药机器人作为特殊的运动体,假如取药机器人在前进的过程中与药架或者其他障碍物没有保持一定的安全距离,那么取药机器人在实际运行中难免与药架等障碍物发生碰撞,严重的话不仅会损坏机器人本体,还会导致药架上的药盒跌落[11]。
基于上述分析,主要对栅格地图中的障碍物(药架)进行膨胀处理。在对障碍物进行膨胀处理的同时,需要将取药机器人的外部特征(长、宽、高等)考虑在内。通常药房机器人的高度在1.2 m,宽度在0.3 m左右,两个药架之间的距离一般在1.2 m左右,一个药架的宽度在0.3 m,因此将药架膨胀半径设定为机器人宽度的一半左右,这样机器人在药房过道中规划出的路径与障碍物的最小距离大于机器人宽度的一半,能够保证取药机器人本体的宽度小于两个药架之间可通行的区域。对障碍物进行膨胀处理旨在帮助取药机器人安全地穿行各药架之间。
2.2.2 轨迹优化
A*算法规划出的路径不仅要符合机器人运行安全规范,避免与障碍物发生碰撞,还要保证路径转折点较少,平滑性高。若规划路径转折较多意味着机器人在实际运行途中需要多次改变运行方向,不仅会降低机器人取药效率,而且还会提高机器人在拐弯时药品滑落的风险。因此,在基于对障碍物的膨胀处理基础之上,提出评价函数引入安全因子,并在转弯处使用圆弧曲线来代替尖锐点来解决转折点较多、碰撞威胁较大的问题,进一步提高A*算法规划路径的可采用性[12-13]。改进的评价函数为
(4)
式中:(x,y)为当前被搜索节点;f(x,y)为估计成本;g(x,y)为实际成本;h(x,y)为启发函数,本文使用Manhattan距离;A为当前点到目标点的距离;a为起始点到目标点的距离;n为药架占总栅格的总数;L为机器人自身所占栅格的数目;N*M为总栅格数量;γ为安全因子。
在完成对A*算法评价函数改进的基础之上,为了使得到的路径更加平滑,使用几何法来剔除路径冗余点与不必要的转折点,结合平滑的圆弧来改进转弯时的尖锐点,对路径进行优化处理。文献[14]通过计算任意两点斜率是否相等来判断路径中三点共线的问题,但忽略了实际情况中斜率可能不存在,或者为0等特殊情况。本文使用三阶行列式面积法解决路径中三点共线的问题。假设路径上的某一节点坐标(x1,y1)以D表示,节点D的前一节点坐标(x0,y0)以C表示,节点D的后一节点坐标(x2,y2)以E表示。则其所围成的三角形面积为
(5)
如果S△等于零时,说明C、D、E三点共线,那么节点D为冗余点,需剔除,路径由C到D再到E直接变为由C到E。

(6)
(7)
(8)
(9)
其中:μ1、μ2、μ3、μ4均为叉积的系数。如果μ1·μ2<0,且μ3·μ4<0,如图4所示,则表示角平分线FI与线段CE相交;如图5所示,则表示线段CE与角平分线不相交。其余两条角平分线与线段CE是否相交也可根据此原理判断。其实只要三条角平分线中的任意一条与线段CE相交,则代表节点C与节点E之间有障碍物,路径仍然是由C到D再到E(不改变其路径);反之,如果三条角平分线和线段CE都没有相交,则代表节点C与节点E之间并无障碍物,连接节点C与节点E,去除冗余节点D,路径由C到D再到E直接变为由C到E[14]。
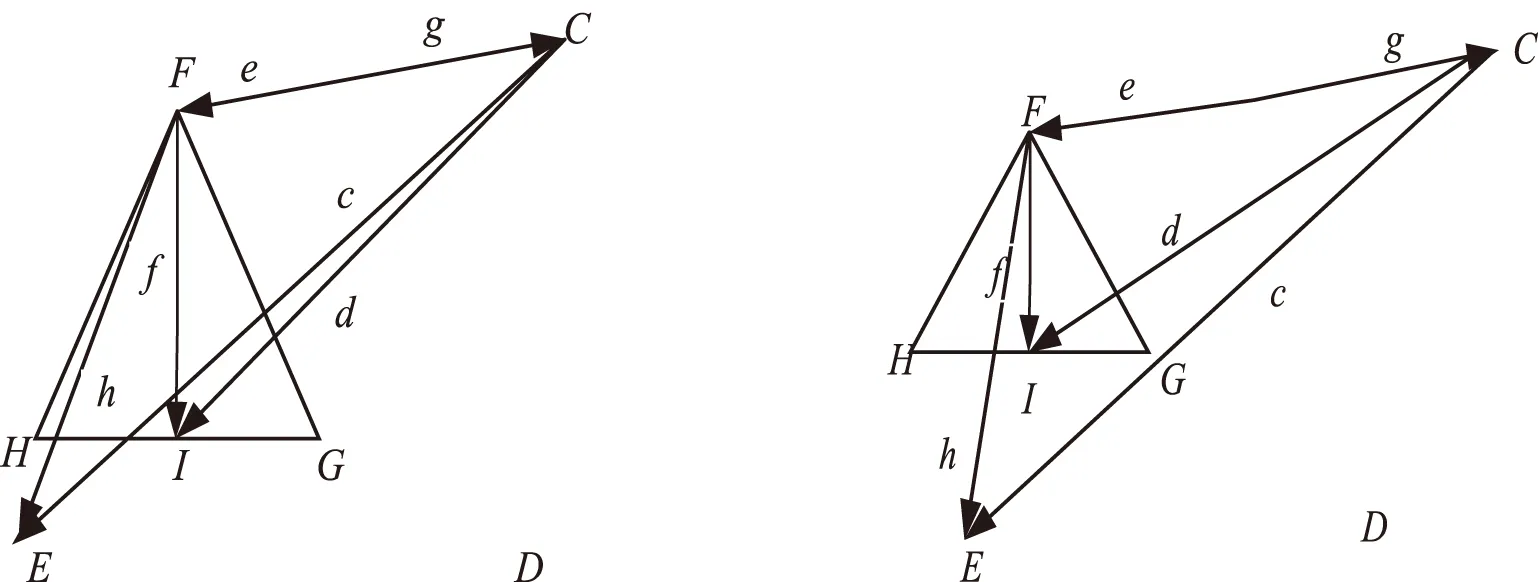
图4 节点之间存在障碍物 图5 节点之间不存在障碍物
3 仿真实验与分析
在栅格地图中为取药机器人设置3组不同起始点与目标点的坐标,且随机产生3个取药任务(任务信息如表1所示),每个任务由一台机器人完成,一旦确定目标点将会开始路径规划。从3个方面分别对标准A*算法和改进后的A*算法进行评价:一是计算时间;二是优化路径长度;三是路径的平滑度。实验分为两组,分别基于简单地图和复杂地图进行。实验结果如表2所示,仿真图如图6和图7所示。

表1 机器人任务信息

表2 实验结果对比
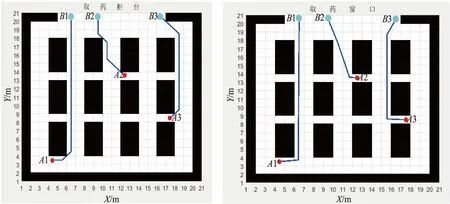
(a)标准A*算法 (b)改进A*算法图6 基于简单地图的仿真实验结果

(a)标准A*算法 (b)改进A*算法图7 基于复杂地图的仿真实现结果
图6和图7中A1、B1代表的是第一个机器人的起始点与目标点,A2、B2、A3、B3分别代表的是第二个、第三个机器人的起始点与目标点。不考虑各取药机器人任务下达等时间问题。从图6和图7中可以明显看出,改进后的A*算法所规划的路径比标准A*算法所规划出的路径能够与障碍物保持安全距离,路径更加平滑,在优化路径的同时,也能节约规划的时间。
4 结 语
为解决自动化药房中取药机器人路径规划问题,提出一种对障碍物进行膨胀处理的改进A*算法,该算法可以有效地优化机器人路径规划,提高机器人工作效率。为验证算法的有效性,在构建栅格地图的基础上,设计了两组具有不同起始点、目标点和障碍物的仿真实验。经仿真验证,改进的A*算法可以增强路径搜索灵活性和安全性,提高其搜索效率,在实际自动化药房路径规划系统中具有一定的现实意义。
