基于贝叶斯模型的羊绒羊毛识别
2021-07-14朱耀麟张春风穆婉婉
朱耀麟 张春风 武 桐 穆婉婉
(西安工程大学,陕西西安,710048)
目前羊绒纤维与羊毛纤维的鉴别方法有显微镜检测法[1]、近红外光谱法[2]、DNA检测法[3]、图像处理与计算机视觉的方法[4]。当前的研究热点是图像处理与计算机视觉技术这个方向。周剑平等提出了一种利用贝叶斯网络和电镜扫描图像结合的方法鉴别羊绒羊毛纤维[5]。首先对纤维图像进行图像预处理,步骤为先二值化,然后确定边界线,再分割纤维图像;在分割后的边缘图像中提取纤维的鳞片高度和纤维直径,最后将提取到的特征输入到贝叶斯网络分类。由于只提取了鳞片长度和纤维细度两个参数,没有考虑其他参数对鉴别的影响,具有一定的局限性[6]。杨建忠等研究了羊绒和羊毛电镜扫描图像的表面形态,测量了鳞片周长、鳞片面积、鳞片厚度、纤维直径、鳞片高度等几个直观指标,再通过计算得到鳞片的内方形因子和外方形因子等2个相对指标[7]。彭伟良等首先对羊毛和羊绒的电镜扫描图像进行阈值分割,再提取羊绒羊毛纤维的直径、鳞片面积、鳞片周长等几何参数,对这些参数进行统计分析,建立纤维种类判鉴别模型[8]。上述研究者的方法都只分析利用了单一特征参数或者几个简单的特征参数结合,对多个特征参数缺少统计分析,因此在鉴别精度上有一定的局限性。当前,鉴别精度高、重复性较好的鉴别系统基本都是基于扫描电镜(SEM)[9],因为SEM图像景深大、分辨率高,所得到的显微图像结构清晰、纹图较明显,在图像分类和目标检测中具有很好的效果。
1 研究方法
本研究以SEM图像为基础,首先对SEM图像进行预处理,然后提取纤维骨架特征参数,再对羊绒羊毛纤维特性参数的分布进行统计分析,比较各个参数间的相关性和正判率,从而选择最合适的鉴别参数,最终利用这些参数建立贝叶斯模型[10-11]。该系统对羊绒羊毛进行检测的流程如图1所示。
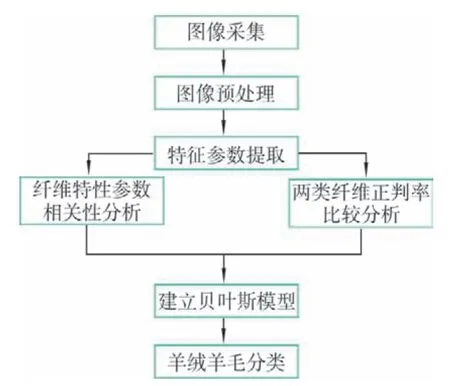
图1 算法流程
1.1 纤维图像的骨架提取
直接拍摄的原始图片中会存在很多干扰因素,例如图片背景的亮度不均匀,存在杂质、噪声等情况。为更准确方便地提取纤维的特征参数,需要对图片进行预处理,去除与特征参数无关的一些因素和干扰,只保留纤维最主要的特征部分。
羊绒纤维SEM图像骨架提取如图2所示。首先通过调整原始图像的灰度值对图像进行增强,增强后的图像如图2(b)所示。然后使用全局阈值方法将纤维图像二值化,如图2(c)所示。二值化后纤维的轮廓和特征都得到了明显的增强,但是噪声也被增强了,所以要对纤维图片进行去噪。首先通过孔洞填充的方法将纤维区域的黑色像素去除,然后分别计算各个封闭区域的像素个数,只保留最大面积区域,去除小面积区域,从而达到去除噪声的目的,效果如图2(d)所示。直接对图2(d)进行细化,会得到一个如图2(e)所示的毛刺效果图。提出建立两个纤维骨架模板,首先对噪声去除后的图2(d)进行闭运算,得到一个包含纤维轮廓所有信息的背景模板,如图2(f)所示。再对原始图像进行闭运算得到轮廓图像,然后进行二值化,可以得到原始模板,如图2(g)所示。把原始模板和背景模板进行叠加后得到叠加效果,如图2(h)所示。最后再进行细化操作得到最终细化效果,如图2(i)所示。

图2 羊绒纤维SEM图像骨架提取
1.2 特征参数的提取
对羊绒和羊毛的纤维样本进行特征参数提取。羊绒羊毛纤维的直接特征参数有纤维直径、鳞片密度、鳞片高度、鳞片周长、鳞片面积。相对特征参数有面积比、周径比、径高比、方形度,它们都可以通过直接特征参数计算得到。面积比Ad=A/d²,A为纤维的鳞片面积,d为纤维的直径;周径比Pd=P/d,P为纤维的鳞片周长;径高比dh=d/h,h为纤维的鳞片高度;方形度SR是指鳞片与正方形的近似情况,SR=A/(P/4)²。
在测量纤维的直径时,认为纤维两侧的边缘线是平行的,先得到纤维的中轴线,然后每隔5个像素,做中轴线的垂线,这些垂线与纤维的两侧边缘线存在交点,每对交点的距离作为纤维的直径。测量鳞片面积时将鳞片区域块内的部分填充为白色,统计封闭区域块内部像素个数作为鳞片面积;将区域块分别提取出来,统计区域块边缘像素个数作为周长。假设纤维中轴线与鳞片边缘的交点有N个,L为中轴线长度,鳞片高度则为L/(N-1)。具体如图3所示。

图3 特征参数的测量
1.3 两类纤维的误判率分析
提取羊绒羊毛纤维图像各500幅,对它们的特征参数进行统计分析。图4为羊绒、羊毛的鳞片高度特征分布直方图。

图4 鳞片高度特征分布图
从图4可以容易地发现羊绒羊毛纤维鳞片高度的分布为正态分布,拟合度分别为0.974和0.643,得到的拟合方程见式(1)。通过拟合方程计算可得羊绒鳞片高度的拟合参数为y0=0.007 85、w=0.160 41、xc=13.130 21,A=0.886 99,羊毛鳞片高度的拟合参数为y0=0.012 39、w=0.263 69、xc=10.537 01、A=1.213 14。

式中:y0表示基线函数,A为拟合曲线与x轴面积,xc为鳞片高度,w为纤维分布的对数均方差。
图4能清楚直观地看到羊绒和羊毛的鳞片高度存在的差异,以羊绒羊毛鳞片高度为例,研究鳞片高度对羊绒羊毛纤维鉴别的影响因子。鳞片高度的特征分布曲线差异如图5所示。
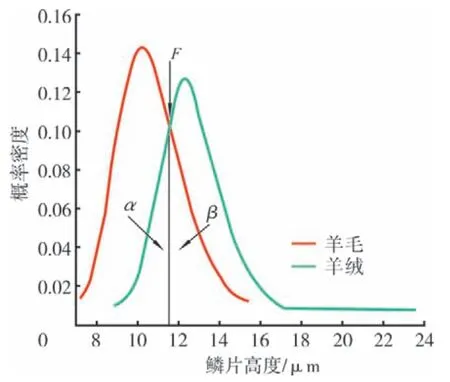
图5 鳞片高度特征分布对比
将羊绒羊毛鳞片高度特征分布图的拟合曲线进行叠加,能够发现两曲线交于F点。当鳞片高度大于F点横坐标时,羊绒的概率密度大于羊毛概率密度;当鳞片高度小于F点横坐标时,羊毛的概率密度大于羊绒概率密度。通过计算得到F点横坐标为11.743μm。选择F点为羊绒羊毛的判别点,当鳞片高度大于11.743μm时,认为是羊绒纤维;当鳞片高度小于11.743μm时,认为是羊毛纤维。图5中,设羊绒拟合曲线与x轴和直线x=11.743形成的区域为α,表示羊绒被错判成羊毛的概率;设羊毛拟合曲线与x轴和直线x=11.743形成的区域为β,表示羊毛被错判成羊绒的概率,通过计算得到α=0.256,β=0.406,Ac=α+β=0.662。进而引入正判率γ,见式(2)。

计算得到鳞片高度的正判率为0.505。根据以上原理,得出纤维直径、鳞片密度、鳞片周长、鳞片面积、周径比、面积比、径高比、方形度的正判率分 别 为0.869、0.752、0.504、0.497、0.756、0.703、0.683、0.396。正判率大小排序为:纤维直径>周径比>鳞片密度>面积比>径高比>鳞片高度>鳞片周长>鳞片面积>方形度。
1.4 鳞片特征相关性分析
提取了羊绒羊毛各500个样本的鳞片特征,对这1 000个样本的鳞片特征参数进行了研究,如图6所示。由图6(a)可知,纤维直径d越大,鳞片周长P也随着变大,它们的相关系数R=0.857,鳞片周长和纤维直径呈正比关系,拟合方程为P=18.964+2.621d。由图6(b)可知,纤维直径d和鳞片高度h的相关系数R=0.119,两个参数不相关。由图6(c)可知,鳞片面积A随着鳞片周长P的增大呈非线性递增,拟合曲线方程为A=598.214-586.028/[1+e(P-75.227)/25.102],两 个 参 数的相关系数R=0.969。

图6 参数相关性
将所有参数之间的关系进行统计,得到参数间相关系数见表1。纤维的鳞片直径越大,鳞片面积和鳞片周长也越大,因此在选择参数的时候应该剔除掉鳞片面积和鳞片周长,以便于简化鉴别工作量。由表1可知纤维直径、鳞片高度、鳞片密度、面积比、周径比、径高比、方形度这7个特征参数间的相关性较小,如果我们单从相关性上选择参数,应该选择这7个参数作为鉴别指标。

表1 特征参数间相关系数表
2 试验部分
本研究所用纤维试样取自陕北的绒山羊,由榆林科学技术局提供。对羊绒羊毛纤维进行梳洗、筛选、制样,然后利用扫描电子显微镜拍摄羊绒和羊毛纤维的图片。制样方法采用GB/T 14593—2008《山羊绒、绵羊毛及其混合纤维定量分析方法》。采用的试验设备为FEI Quanta450FEG型台式扫描电子显微镜,放大倍数为1 000倍。
统计分析1 000个羊绒羊毛样本特征参数的分布,依据在参数间相关性小、正判率高的前提下,参数尽量少的原则,选择了纤维直径、鳞片高度、鳞片密度、面积比、周径比、径高比6个参数建立贝叶斯模型。
将纤维直径、鳞片高度、鳞片密度、面积比、周径比、径高比6个特征参数组成特征向量x=(x1,x2,x3,x4,x5,x6)。设纤维为羊绒时的条件 为ω1,纤 维为羊毛时 的 条件为ω2,则P(ωi|x)(i=1,2)是x=(x1,x2,x3,x4,x5,x6)属于ωi的 条 件概率。
设P(ω1|x)<P(ω2|x)时,判定纤维为羊毛,反之判定纤维为羊绒。假设两种纤维的概率相同,即P(ω1)=P(ω2),则P(ω1|x)与P(ω2|x)的大小可以通过比较P(x|ω1)与P(x|ω2)的大小来实现。特征参数的权系数λj可由正判率γj计算得到,见式(3)。

经计算,纤维直径、鳞片高度、面积比、周径比、径高比、鳞片密度的权系数分别为0.216、0.093、0.183、0.187、0.153、0.168,权系数大小关系为:纤维直径>周径比>面积比>鳞片密度>径高比>鳞片高度。权系数越大,参数鉴别能力越强。

运用采集到的羊绒羊毛纤维样本各500个,对建立的六参数贝叶斯模型进行验证,并且与传统的只利用纤维直径、鳞片周长和鳞片面积等简单参数的鉴别模型进行对比,具体的鉴别效果见表2。试验结果表明,通过这6个特征参数建立的贝叶斯模型识别精度比传统的只利用纤维直径、鳞片周长和鳞片面积等简单参数识别精度高得多,接近95%,达到了预期的效果。

表2 六参数模型和传统模型正确率比较
3 结论
本研究过程分析了很多羊绒羊毛纤维的特征参数,对纤维特征参数的分布进行了统计分析,对各特征参数间的相关性进行了分析,还研究了各参数对羊绒羊毛正判率的影响,最终选择了纤维直径、鳞片密度、鳞片高度、周径比、面积比、径高比6个参数建立了贝叶斯模型。结果表明,本方法对鉴别羊绒羊毛纤维有着很高的精确度。而且,由于检测性质的相似性,此方法还可以用在狐狸毛、兔毛等其他动物毛发中,有着很大的应用前景。
