大跨径小半径曲线桥梁转体结构设计

陈爱荣

［上海市政工程设计研究总院（集团）有限公司，上海市200092］

0 引言

桥梁转体施工按旋转方向可分为平转法、竖转法以及平竖转相结合的工法[1]。一般平转法桥梁平面线形通常为直线或大半径曲线。近年来，逐步出现了小半径曲线桥梁的转体施工，相比之下，小半径曲线桥梁的转体结构设计更复杂。对于跨径较大的桥梁，转体结构的稳定性往往成为设计关注的重点。本文以宁波市轨道交通4号线跨铁路转体桥为例，介绍大跨径小半径曲线悬浇桥梁转体结构的设计要点。

1 工程概况

宁波市轨道交通4号线在右转出江北大道后，小角度（约30°）斜交上跨萧甬铁路、杭甬客专，线路曲线半径仅350 m。

跨铁路节点桥现状桥位见图1。

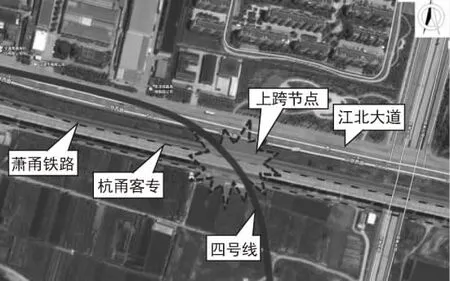
图1 跨铁路节点桥现状桥位

萧甬铁路交叉段为路基段，采用混凝土轨枕，有碴轨道；杭甬客专为高速铁路，设计时速350 km/h，交叉段为高架桥，总宽约12 m。为了减小本工程对既有线路的影响，桥梁方案采用跨径布置为68 m+138 m+95 m=301 m的预应力混凝土刚构桥，主跨1孔跨越现状铁路，北侧承台边缘（墩号QJ01D027）距萧甬铁路中心线9.1 m，南侧承台边缘（墩号QJ01D028）距杭甬客专中心线20.9 m，满足铁路保护施工安全距离要求。先在铁路两侧浇筑桥墩及主梁，浇筑完毕后，进行转体施工，转体就位后合龙成桥。

跨铁路节点桥平面布置如图2所示。

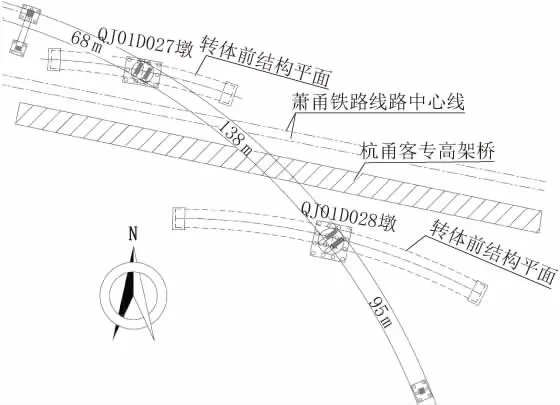
图2 跨铁路节点桥平面布置图

2 主要技术标准

（1）最高运行速度v=80 km/h。

（2）车辆：B型车，6辆编组，轴重不大于14 t。

（3）线路：双线，线间距为4.2 m。

（4）桥梁宽度：11 m。

（5）设计使用年限：100 a。

3 转体结构设计

3.1 总体设计

转体结构由上转盘、球铰、下承台、转体牵引系统组成[2]。在转体过程中，上转盘、下承台通过球铰传力，呈现多维受力状态，均需布置双向多层预应力钢束。

QJ01D27墩转体质量约7 700 t，T构总长100 m，转体角度19°，上转盘平面为φ12 m圆形，厚2.5 m，下承台平面为14 m×19.4 m矩形，厚3.5 m，下设12根直径2.0 m钻孔灌注桩基础；QJ01D28墩转体质量约14 600 t，T构总长172 m，转体角度40°，上转盘平面为φ15 m圆形，厚3.0 m，下承台平面为19.4 m×19.4 m矩形，厚4.0 m，下设16根直径2.0 m钻孔灌注桩基础。上转盘、下承台间布置撑脚及砂箱，转体完成后浇筑厚0.8 m的封铰混凝土。

转体牵引系统由中心对称的2束钢绞线组成，钢束锚固于上转盘内部，如图3所示。QJ01D027墩转体启动牵引力739 kN，选用11-φs15.2钢绞线，启动时钢绞线应力480 MPa，安全系数为3.8；QJ01D028墩转体启动牵引力1 511 kN，选用21-φs15.2钢绞线，启动时钢绞线应力514 MPa，安全系数为3.6。

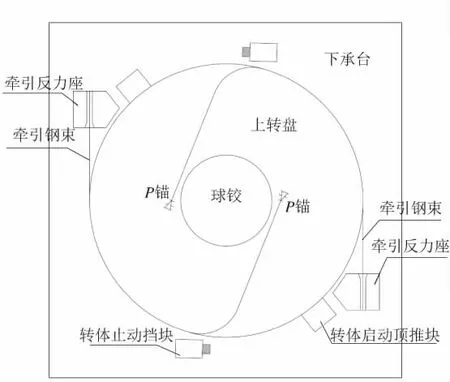
图3 转体牵引系统示意图

3.2 球铰的选用

球铰一般采用厂家成套产品，可以根据转体吨位确定球铰的材料及尺寸。

球铰材料有钢材及混凝土2种，混凝土球铰一般适用于转体吨位6 500 t以下的桥梁，本桥转体吨位较大，故选用钢球铰。

根据转体吨位，可按表1选用球铰的磨心支承半径R1，再按表2选用球铰的半径R。

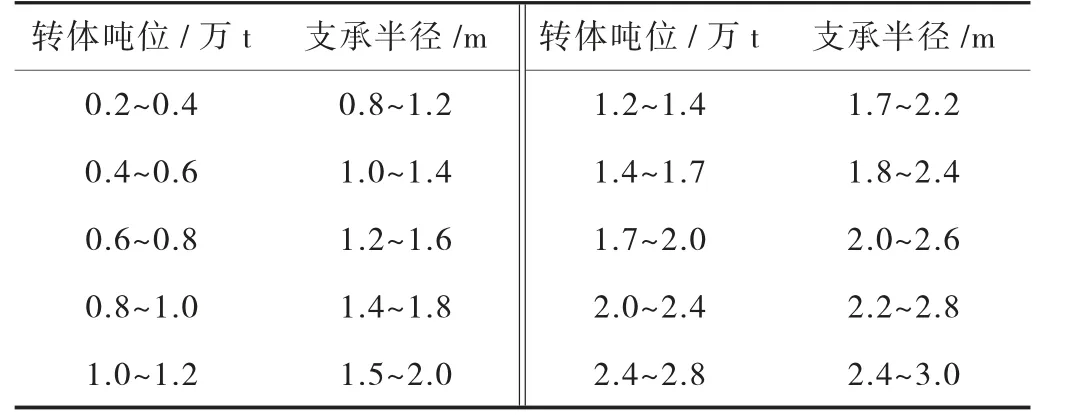
表1 不同转体质量下的球铰支承半径取值范围

表2 不同支承半径的球铰半径取值范围

本桥转体墩位分别为7 700 t和14 600 t，故相应的球铰磨心支承半径R1和球铰半径R分别选用1.5 m、7 m和2 m、8 m，设计过程中实体建模分析，保证球铰在转体时全程受压且不被压坏。

3.3 转盘中心预偏设置

曲线桥上部结构自重会引起横向不平衡弯矩。本桥位于小半径曲线上，最大悬臂状态下墩底横向偏心弯矩QJ01D027墩为50 085 kN，QJ01D028墩为251 410 kN，偏心弯矩过大。配重平台因配重量小，力臂较短而平衡偏心弯矩能力有限，故需通过设置转盘中心预偏以抵消曲线梁上部结构恒载横向偏心。横向预偏值可通过墩底横向不平衡弯矩除以转体质量求得，方向与横向不平衡弯矩引起的偏心方向相同。

通过计算，本桥QJ01D027墩转盘中心设置0.8 m横向预偏心，QJ01D028墩转盘中心设置2.5 m横向预偏心，桥墩采用矩形空心截面，横向立剖面单侧变宽以调整偏心，如图4所示。

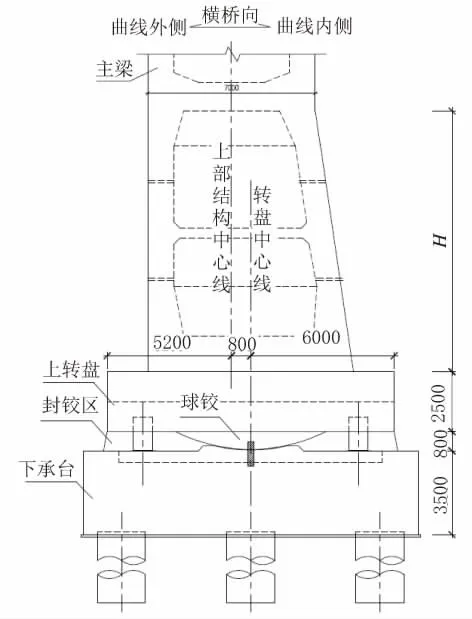
图4 转盘中心预偏设置示意图（以QJ 01D027墩为例）（单位：mm）

3.4 悬浇阶段稳定性分析

转盘中心横向预偏为基于T构施工至最大悬臂状态时设置，对于施工至各节段的悬臂状态则会存在与偏心设置方向反向的弯矩；考虑悬臂浇筑施工的先后顺序、风荷载的方向、施工机具的布置等因素也会造成荷载的不对称，故需对悬浇各节段的抗倾覆稳定性进行验算。

3.4.1 计算模型

采用计算软件Midas/Civil建立悬浇阶段曲线杆系模型，进行悬臂浇筑施工模拟。下部结构建至上转盘为止，在球铰位置处施加固结边界条件，计算模型如图5所示。

图5 悬臂浇筑阶段模型（以QJ 01D027墩为例）

3.4.2 计算荷载

计算荷载主要考虑引起悬浇阶段转体结构倾覆风险的荷载。

自重：混凝土容重按26 kN/m3计算，软件自动计算。

风荷载：分别考虑9级风（25 m/s）与百年一遇风（31.3 m/s）在施工过程中引起的横向风荷载、纵向风荷载以及风举力。风举力P=CLwA，式中：w为基本风压；A为水平投影面积；CL为风举力系数，取0.75[3]。

挂篮荷载：取悬臂施工最大节段质量的40%计算，作用点位于下一节段中间位置。

施工误差荷载：考虑施工节段时产生±2.5%的质量误差。

3.4.3 工况组合

3个因素在Y1模型上对F值的响应值的影响由大到小依次为：一次项>二次项>交互项，由P值可以看出一次项对实验结果的影响是极显著的；3个因素在Y2模型上对F值的响应值的影响由大到小依次为：二次项>一次项>交互项，从P值反映的结果来看，实验结果受二次项影响较为显著，交互项对结果的影响相对较弱。由回归P值可以看出，Y1模型显著，Y2模型极显著，说明由这2个模型代替实际实验点进行分析途径可行，结论可信。

假定转体结构纵桥向重心线两侧分别为A、B侧，横桥向重心线两侧分别为C、D侧，如图6所示。

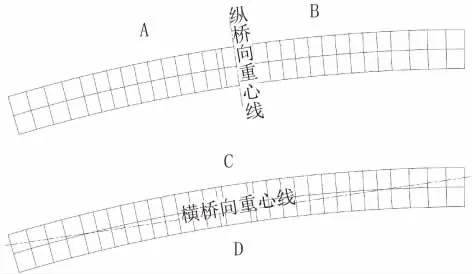
图6 转体结构重心线划分

验算悬臂浇筑阶段抗倾覆稳定性时考虑如下4种荷载工况：

（1）A侧恒载重102.5%+B侧恒载重97.5%+对称挂篮+A侧箱梁多浇筑1/2节段+A侧有50 kN施工机具+顺桥向9级风载+B侧风举力。

（2）A侧恒载重102.5%+B侧恒载重97.5%+对称挂篮+顺桥向百年一遇风载+B侧风举力。

（3）C侧恒载重102.5%+D侧恒载重97.5%+对称挂篮+A侧箱梁多浇筑1/2节段+A侧有50 kN施工机具+横桥向9级风载。

（4）C侧恒载重102.5%+D侧恒载重97.5%+对称挂篮+横桥向百年一遇风载。

工况（1）、工况（2）为纵桥向重心线单侧最不利布置工况；工况（3）、工况（4）为横桥向重心线单侧最不利布置工况。

3.4.4 结果分析

转体结构抗倾覆失稳力矩为T=R’×F，其中：R’为球铰体系的环道半径；F为转体结构球铰以上部分的总重。提取4种工况下施工每个节段时球铰底部的轴力F以及2个方向的弯矩Mx、My，计算合弯矩M=（Mx2+My2）×0.5，即可求得抗倾覆稳定系数k=T/M=R’×F/M，如图7所示。

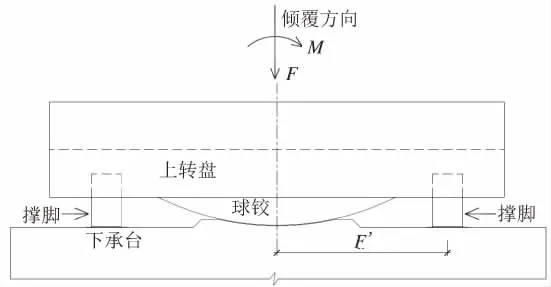
图7 悬浇阶段抗倾覆失稳图示

QJ01D27、QJ01D28墩在4种荷载工况下施工每个节段时抗倾覆稳定系数的变化规律如图8、图9所示。

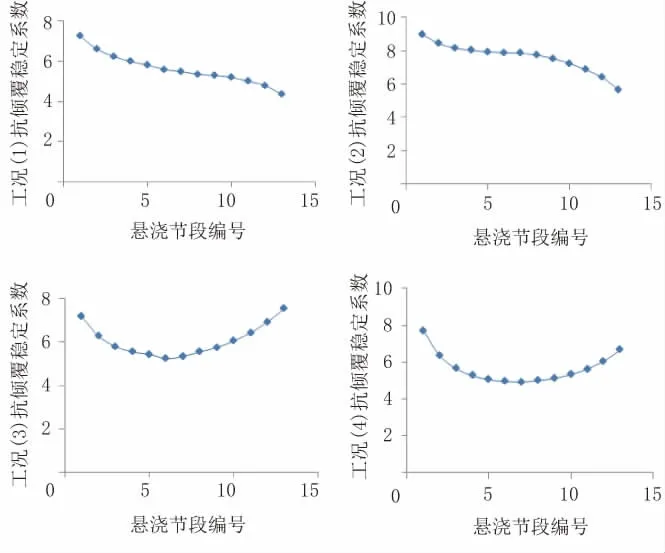
图8 QJ 01D27墩各工况下抗倾覆稳定系数变化图

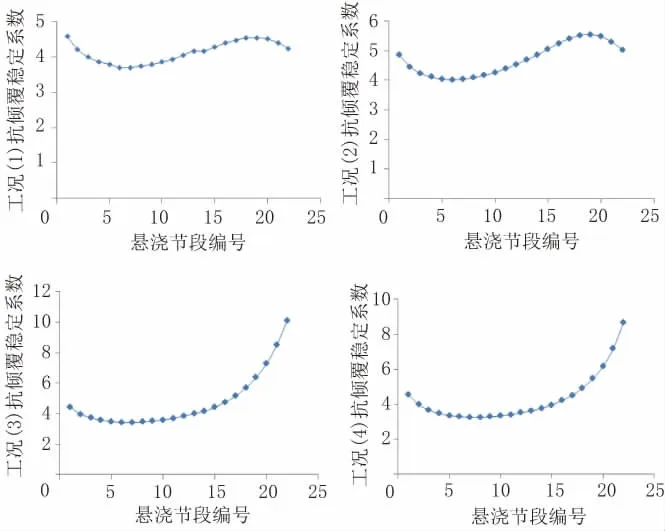
图9 QJ 01D28墩各工况下抗倾覆稳定系数变化图

由图8、图9可知，本桥4种最不利工况下，悬浇阶段结构的抗倾覆稳定性均能满足规范要求。分析抗倾覆稳定系数随悬浇节段的变化规律发现，纵向不平衡荷载作用下（工况（1）、工况（2）），抗倾覆稳定系数整体呈现正弦曲线变化规律，最小值在1/4跨或全跨附近；横向不平衡荷载作用下（工况（3）、工况（4）），抗倾覆稳定系数呈现近似抛物线变化规律，先减小再增大，最小值在1/4跨或半跨附近。对于悬浇阶段结构的抗倾覆稳定性验算，本文推荐选取悬浇至1/4跨、半跨以及全跨时的受力状态进行计算分析。

3.5 转体阶段稳定性分析

转体结构除了要满足悬浇阶段的抗倾覆稳定性要求，还需满足转体阶段的抗倾覆稳定性要求。转体过程中，球铰发生如图7所示的倾覆失稳模式，以撑脚为轴发生倾覆失稳。

倾覆荷载考虑9级风（25 m/s）在施工过程中引起的横向风荷载、纵向风荷载以及风举力，上部恒载剩余偏心按配重调偏后0.2 m计，并考虑撑脚下移10 mm引起的重心附加偏移。撑脚与环道的几何相对位置如图10所示[4]。

图10撑脚与环道的几何相对位置关系

图10 中参数间有如下关系：

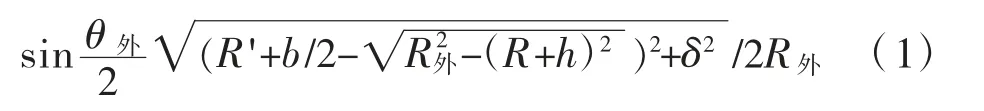
式中：R外为撑脚外边缘的旋转半径，其表达式为：

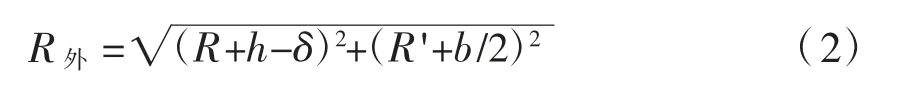
转体结构的重心位置偏不利地取于梁顶，通过撑脚下移值10 mm计算得到球铰发生的转角θ外，可得重心附加偏移值：

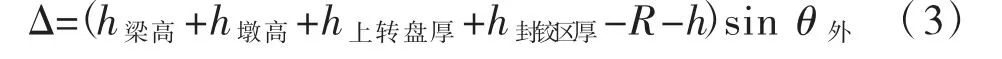
分别计算转体阶段横向和纵向的抗倾覆稳定系数。横向风荷载及相应风举力引起的倾覆弯矩为M横，纵向风荷载及相应风举力引起的倾覆弯矩为M纵，则转体阶段的横向抗倾覆稳定系数k横、纵向抗倾覆稳定系数k纵分别为：

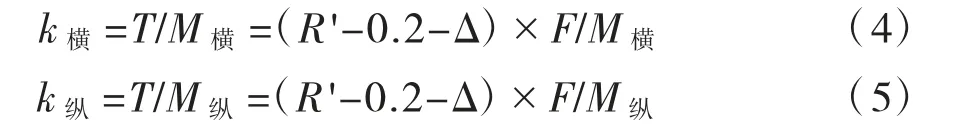
本桥转体阶段QJ01D27墩横向抗倾覆稳定系数k横为32.7，纵向抗倾覆稳定系数k纵为56.3；QJ01D28墩横向抗倾覆稳定系数k横为42.7，纵向抗倾覆稳定系数k纵为75.0，均能够满足抗倾覆稳定要求，且富余很大。分析结果不难发现，设置转盘预偏及配重调偏后的转体结构，不平衡弯矩已大大降低，只需施工精度控制得当，一般不会发生转体阶段的倾覆失稳。

4 结 语

本文基于宁波市轨道交通4号线工程跨铁路转体桥，从转体结构的总体组成、球铰的选用、转盘预偏心的设置、悬浇阶段结构的稳定性、转体阶段结构的稳定性等方面阐述了大跨径小半径曲线转体桥转体结构的设计要点、计算方法等，总结了此类桥梁悬浇阶段结构的抗倾覆稳定性规律，提出悬浇阶段结构的抗倾覆稳定性验算关键节点为施工1/4跨节段、半跨节段以及最终节段；转体阶段结构的抗倾覆稳定性系数一般富余较大，不会发生转体阶段的倾覆失稳。所得结论可为同类工程项目提供参考。