基于粒子云方法研究地磁场对运动电子束的时空分布影响

冯明航，付松，倪彬彬，雷良建，焦鹿怀

（武汉大学电子信息学院，武汉 430072）

0 引言

地球空间存在大量的带电粒子束结构[1-2]，一般而言，自然的电子束往往可以由波粒相互作用产生的粒子沉降或者等离子体不稳定性引起[3-6]。这些粒子束中的带电粒子往往具有很高的动能和很强的方向性，因此不但可以影响空间天气和空间环境[7]，还可能通过总剂量辐射损伤、单粒子效应和充放电效应等对运行在地球空间的人造天体造成潜在的重要危害[8-10]。长期以来，空间环境中的带电粒子束尤其是电子束一直是空间物理学的重要研究内容，科学家通过天基、地基观测，理论分析以及数值模拟来研究电子束在空间环境中的形成、演化以及消亡等关键过程[11-12]，希望能够准确预测电子束的时空分布来降低或者避免其对人造天体的危害。

研究电子束在地球空间环境所起作用的一个重要问题是，电子束在传输过程中自场效应以及对背景地磁场的响应的空间电荷效应耦合结果，将如何影响电子束的结构形态以及电子束本身的相空间演化[13]。一般而言，电子束在运动过程中，带电粒子相互之间受库仑斥力影响，会产生横向结构上的发散以及纵向结构上的拉伸；此外带电粒子受外在电磁场所产生的洛伦兹力影响，会沿外在电场方向加速并围绕外在磁场发生偏转[14]。以上多种效应耦合在一起，构成了研究电子束空间电荷效应的物理机制背景。针对此复杂的多物理机制耦合问题，常用的研究方法有：1）基于电荷中和的电子束传输线性解析理论，以求解电子束包络方程为手段研究电子束空间电荷效应的演化问题[15]；2）基于单粒子运动方程的试验粒子方法，以求解带电粒子的单粒子运动方程来描述典型粒子的运动轨迹[16]。方法1 对于电子束传输的低阶线性和单一物理过程可以给出非常直观的物理解释，例如无背景场的电子束空间电荷效应问题，但是对于研究非线性物理过程和多物理机制耦合过程则比较乏力；方法2可以很好地描述单一参考粒子对外加电磁场的运动响应，但是无法体现电子束内部带电粒子之间相互作用的效果。针对以上两种方法的优势和不足，需要使用Vlasov-Poisson 动理论来研究电子束的空间电荷效应问题[17]；而粒子云（particle-in-cell,PIC）方法是目前最为有效的解决该问题的数值模拟解法[18-19]，能够完整自洽地描述Vlasov 系统中的粒子相空间以及电磁场时空分布变化，并被广泛应用于空间物理和天体物理、受控热核聚变、等离子体物理和真空电子学等多个领域[20-21]。

为了研究电子束空间电荷效应在地球空间环境中的作用及影响，我们开发了静电模式的PIC代码，并建立了基于PIC算法的数值模型。本文给出了该模型的核心算法、电磁场求解方法、带电粒子运动方程求解方法和数值算法初始化等，并对该算法的可靠性进行验证；进而采用该模型对不同地磁条件下不同能量的电子束的空间电荷效应进行定量分析及对比。

1 理论模型及数值方法

为了定量研究地球空间环境带电粒子束受自场和背景地磁场的联合效应，需要同时考虑由库仑力产生的带电粒子自场效应和由洛伦兹力产生的带电粒子对背景地磁场的响应，因此使用描述带电粒子动力学过程的自洽PIC方法来进行数值建模。

1.1 粒子云模型算法

PIC算法被广泛用来研究带电粒子束空间电荷效应产生的集体效应，该方法能同时处理带电粒子分布对电磁场的影响以及电磁场对带电粒子运动的影响。为此我们开发了针对带电粒子束运动的静电模式PIC 代码（以下简称beamPIC）。如图1所示，算法的主循环包含4个步骤[22]：1）使用CIC（cloudin-cell）方法将电荷分配至离散化的空间网格格点，再求得各空间格点上的电荷密度分布；2）根据网格格点处的电荷密度分布，使用基于快速傅里叶变换（FFT）的积分形式格林函数法求解Poisson 方程，从而得到空间网格点上的电势分布，再对电势进行差分得到网格点上的电场分布；3）利用插值获得每个粒子位置处的电磁场；4）求解洛伦兹方程，利用Boris方法更新粒子速度，再使用蛙跳法求得粒子的坐标。

图1 粒子云模型的核心算法Fig.1 Core algorithm of PIC method

1.2 空间电磁场求解

常用的地球磁场模型包括：

1）以国际地磁学和高层大气物理学协会（IAGA）颁布的国际地磁参考场模型（IGRF）。该模型使用球谐函数拟合地球的内源场；每5年颁布一个新的模型，目前最新版本是2019年12月发布的IGRF-13模型[23]。

2）以Tsyganenko模型为代表的半经验模型。该模型根据卫星的磁场观测数据和物理机制建立，将地球磁场看作内源场和外源场之和。该模型从发布之后不断地添加新的卫星数据来更新模型参数，目前较为广泛使用的版本包括T96和TS05等[24]。

为了简化问题，本研究所使用的空间电磁场包括了由三维偶极子场模型[25]得到的背景地磁场和带电粒子束的空间电荷效应引起的自场两部分。背景地磁场为

式中：ϕ为电势；G为格林函数；ρ为电荷密度分布函数；(x,y,z)为场点坐标；(x',y',z')为源点坐标。由于本文研究自由空间的带电粒子束在地磁场下的动力学过程，所以选取开放边界条件，此时G为

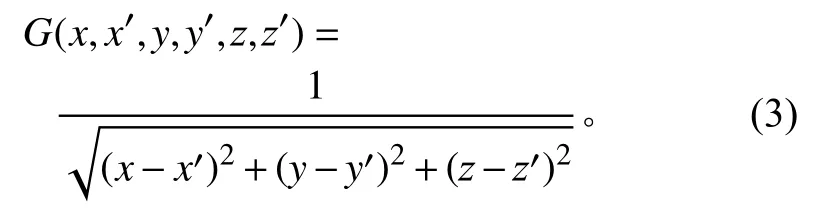
设定模拟区域为三维自由空间中的长方体，其在x、y、z方向上的长度分别为Lx、Ly、Lz，同时在三个方向上的节点数分别为Nx、Ny、Nz，在这些节点上放置点电荷，则任意网格点上的电势为

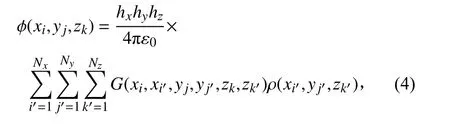
式中：hx、hy和hz分别为x、y和z方向上的网格尺寸；xi=(i−1)hx，yj=(j−1)hy，zk=(k−1)hz；对于奇异值点（i=i'，j=j'，k=k'），G取值为1。利用上式求得ϕ(x,y,z)后，再通过差分求解E=-∇ϕ即可得到该节点上的电场强度。对于式(4)，直接利用卷积数值求和，时间复杂度为N6（N为网格点总数）。为了利用FFT算法本身的周期性特点，并更好地满足开放边界条件，可以使用Hockney Trick 方法[19]，将计算域扩展为2Nx×2Ny×2Nz，同时将格林函数和电荷密度分布函数也拓展至新的计算域空间，计算得到电势后，取实际物理场域Nx×Ny×Nz的值即为空间电荷产生的电势。该方法可将时间复杂度优化至N4lgN。

由上可知，通过使用三维积分形式的格林函数法，可以得到非常准确的空间电场分布，具体实现步骤为：1）根据空间分布范围确定网格尺寸参数；2）利用三维线性加权CIC 方法将电荷分配到邻近的8个网格点上，从而得到 ρD；3）利用三维积分格林函数解析方法求得GD；4)对 ρD和GD作三维FFT 变换，得到和，进而求得；5）对 ϕˆD作三维FFT 逆变换，得到网格点上的 ϕD；6）利用数值差分求解ED=-∇ϕD得到空间电场分布；7）利用插值方法将网格点上的电场插值到粒子所在位置，得到粒子位置处的电场强度。

通过以上数值方法求解Poisson 方程，可以求得电子束空间电荷效应产生的电场分布。

1.3 粒子运动方程求解

由上述方法得到背景地磁场和电子束的自场空间分布，通过带电粒子受力分析可以求得电子穿越电磁场时所受的洛伦兹力。采用数值方法求解描述电子运动的相对论洛伦兹方程，使用具有二阶精度的蛙跳格式来推进粒子运动：首先，粒子运动半个时间步，再通过求解电子束静止坐标系下的泊松方程计算空间电荷效应；通过洛伦兹变换获得实验室坐标系下的电磁场，然后采用Boris方法[26]更新粒子动量；之后粒子再运动半个时间步，重复上述步骤，直至满足停止条件。

带电粒子的运动学方程形式如下：

其中Δt为设置的时间步长。Boris方法广泛应用于数值等离子体模拟中，其具有二阶精度和简洁的数值形式，式(7)和式(10)计算了电场力对粒子动量的作用，式(8)和式(9)计算了磁场对粒子动量的改变。

1.4 算法初始化与终止条件

使用PIC程序，通过读取配置文件进行初始化，参数包含模拟系统环境设置和电子束生成参数，其中：系统环境函数可以设定模拟的时间步长、最大时间步数、模拟空间的网格数、电子束运动距离以及背景磁场等参数；电子束生成函数包含粒子束分布类型、能量、宏粒子数量、电荷量以及质量等参数。对于相空间的电子束，使用电子束尺寸和发射度两个概念来描述电子束在生成和运动过程中的相空间演化情况，包括均方根（RMS）尺寸和均方根偏转角[27]。对于电子束的初始分布，目前主要研究Uniform 分布和Gauss分布等情况。

程序在完成初始化和检查配置文件无误后开始进入PIC算法的循环计算。当电子束满足设定的终止条件如运动最远距离或时间步数达到最大值时程序终止循环。程序运行的每个时间上都可将粒子的位置空间和速度空间的信息记录下来得到完整的电子束演化过程。

2 模拟结果及分析

2.1 初始设定

图2所示为Gauss分布和Uniform 分布的两类电子束在初始时刻的横向尺寸（图上）和偏转角（图下）分布，其中：横向均方根尺寸为5 mm，横向均方根偏转角为0.001 mrad，纵向尺寸为5 mm，纵向能散度为1%，每次模拟所使用的宏粒子总数均为50万个。在后续模拟过程中均使用上述参数生成电子束。

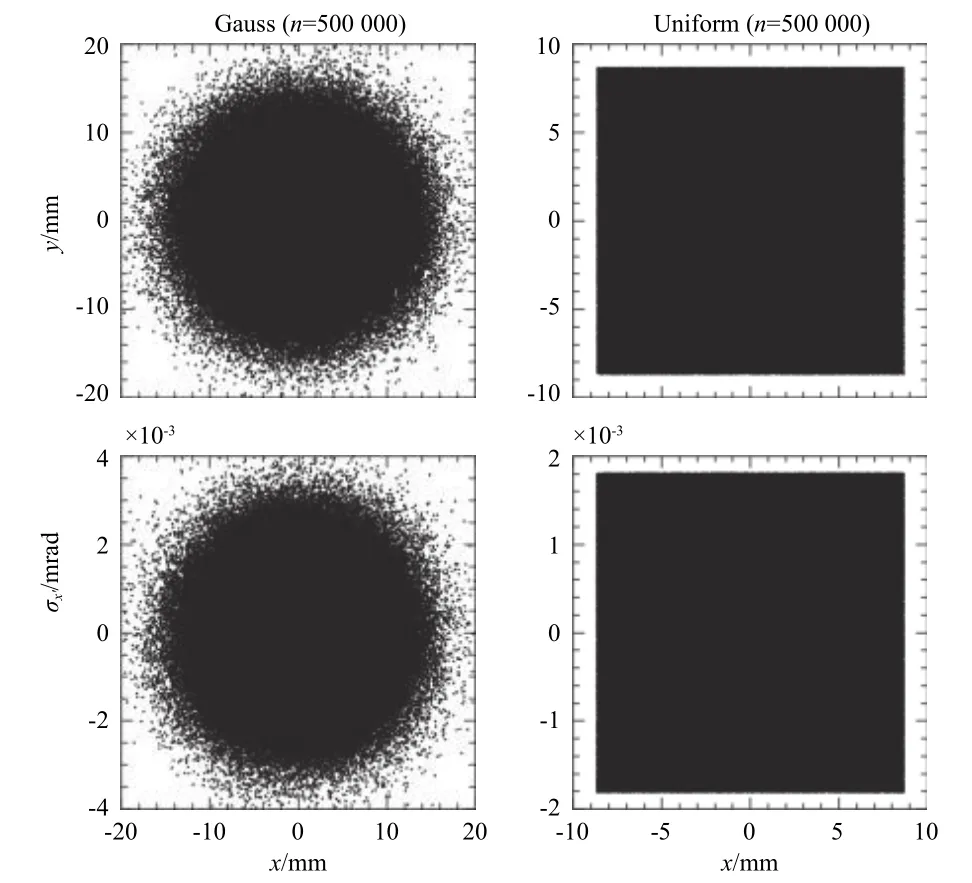
图2 电子束Gauss 初始分布和Uniform 初始分布的横向尺寸和偏转角分布Fig.2 Transverse RMS size and rotation angle of electron beamsfor initial Gaussand Uniform distributions

2.2 可靠性分析

为了进一步验证所开发PIC算法的可靠性，将beamPIC的模拟结果与ASTRA（A Space Charge Tracking Algorithm）软件包的进行对比分析。ASTRA[28]是由德国电子同步加速器研究所发布的空间电荷追踪算法程序，包含了完整的粒子初始分布生成算法和粒子追踪算法等，能够通过PIC算法来计算带电粒子的空间电荷效应等多种集体自场效应，被广泛应用于高能带电粒子的仿真研究。需要说明的是，ASTRA 的算法中假设电子束在纵向具有无限长度，因此只能计算该类电子束的横向四维相空间变化，而我们的beamPIC算法能够研究有限长度电子束的六维相空间变化。

为了对两种方法进行对比，将能量为100 keV的电子束同时输入到beamPIC程序和ASTRA 软件，在相同环境参数设定下，比较电子束传输100 m过程中均方根横向尺寸和均方根偏转角变化情况，结果如图3所示，其中：蓝色实线和红色实线分别为初始Gauss分布电子束的beamPIC和ASTRA模拟结果，黄色虚线和紫色虚线分别为初始Uniform 分布电子束的beamPIC和ASTRA 模拟结果。对于背景磁场，选取了无背景磁场（图3(a)）、与电子束发射方向平行的背景磁场（图3(b)）以及与电子束发射方向垂直的背景磁场（图3(c)）3种情况，地磁场大小取L-shell为5时的磁赤道面磁场大小（由式(1)可知为249.6 nT）。

图3 电子束传输的beamPIC与ASTRA 结果对比Fig.3 Transfer of electron beams obtained by using beamPIC and ASTRA methods

从图3可以看出：当电子束运动距离为100 m时，针对所研究的3种背景场和2种初始分布设定，beamPIC程序和ASTRA 程序结果一致性都非常好，RMS横向尺寸和RMS偏转角变化基本完全吻合；电子束运动至100 m 时，RMS横向尺寸约为230 mm，RMS偏转角约为2.3 mrad。上述结果说明对比ASTRA 软件，beamPIC程序计算结果具有较好的一致性，对于各种初始分布和各种背景磁场情况均能保持很好的数值精度，具有良好的可靠性。

2.3 参量化分析

为了进一步研究不同地磁场影响下电子束运动的空间电荷效应，利用beamPIC程序计算初始Gauss分布和Uniform 分布的两类电子束在不同大小背景磁场作用下运动100 m 时的RMS横向尺寸、偏转角和纵向尺寸变化，来分析电子束在地球磁场和空间电荷效应耦合下的相空间变化情况。为了方便计算，此处只研究了电子束纵向垂直于背景磁场的情况。

在beamPIC的参量计算中，L-shell 分别选取3、4、5、6和7，根据Dipole场模型，计算出背景磁场大小分别为1155.6 nT、487.5 nT、249.6 nT、144.4 nT和91.0 nT。电子束能量分别选取0.1 keV、1 keV、10 keV 和100 keV，图4展示了各能量电子在垂直于背景磁场时的回旋半径。可以发现0.1 keV 电子在L-shell 为3和4，以及1 keV 电子在L-shell 为3时回旋半径小于传输距离100 m，因此在下面的计算中忽略相应的这3种情况。

图4 0.1、1、10和100 keV 电子在地磁场下的回旋半径Fig.4 Cyclotron radius of electrons of energies of 0.1,1,10 and 100 keV in the geomagnetic field

2.3.1 L-shell=3的模拟结果

图5所示为L-shell=3时10 keV 和100 keV 的电子束运动100 m 的RMS横向尺寸、偏转角和RMS纵向尺寸变化情况。其中：黄线表示10 keV 电子束的结果，紫线表示100 keV 电子束的结果；实线表示Gauss初始分布电子束，虚线表示Uniform 初始分布电子束。可以看出两种初始分布的结果在100 m运动距离上比较接近。再以10 keV 电子束为例，从图5可以看出运动100 m 距离时，RMS横向尺寸约为1 m，RMS偏转角约为10 mrad，RMS纵向尺寸约为1.2 m。其中，RMS横向和纵向尺寸的变化主要由电子束自场效应所产生的扩散和拉伸引起，而RMS偏转角的变化主要由对背景场的偏转响应和能量色散引起。此外还可以看到，100 keV 电子束横向和纵向发散明显小于10 keV 电子束，这说明电子束能量越高，自场产生的发散和拉伸效应以及受背景场的影响所产生的电子束相空间的变化越小。

图5 L-shell=3时的模拟结果（B0=1155.6 nT）Fig.5 Simulation results for the case of L-shell = 3(B0 =1155.6 nT)

2.3.2 L-shell=4的模拟结果

图6所示为L-shell=4时的1 keV、10 keV 和100 keV 电子束运动100 m 的RMS横向尺寸、偏转角和纵向尺寸变化情况，其中红色实线和虚线分别表示初始Gauss分布和初始Uniform 分布的1 keV电子束的结果。运动100 m 距离时，1 keV 电子束的RMS横向尺寸约为4 m，RMS偏转角约为35 mrad，RMS纵向尺寸约为3.5 m，其横向、纵向发散程度和偏转角均远大于10 keV 和100 keV 电子束的结果。此外，随着背景磁场的变弱，10 keV 电子束和100 keV 电子束在横向和纵向发散上相较于L-shell为3时有所减小。总之，对于较低能量电子束而言，其回旋半径较小，在运动相同距离上受背景磁场影响更大，同时所需时间更长，因此横向和纵向的相空间变化均最为明显。

图6 L-shell=4时模拟结果（B0=487.5 nT）Fig.6 Simulation results for the case of L-shell = 4(B0 =487.5 nT)

2.3.3 L-shell=5的模拟结果

图7所示为L-shell=5时的0.1 keV、1 keV、10 keV 和100 keV 电子束运动100 m 的RMS横向尺寸、偏转角和纵向尺寸变化情况，其中蓝色实线和虚线分别表示初始Gauss分布和初始Uniform分布的0.1 keV 电子束的结果。从图7可以看到，0.1 keV 电子束运动100 m 距离时，RMS横向尺寸约为17 m，RMS偏转角约为150 mrad，RMS纵向尺寸约为11 m，其横向、纵向发散程度和偏转角均远大于其他3组能量电子束的结果。

图7 L-shell=5时模拟结果（B0 = 249.6 nT）Fig.7 Simulation resultsfor the caseof L-shell = 5(B0 =249.6 nT)

2.3.4 L-shell=6的模拟结果

图8所示为L-shell=6时的0.1 keV、1 keV、10 keV 和100 keV 电子束运动100 m 的RMS横向尺寸、偏转角和纵向尺寸变化情况。可以看出：0.1 keV 电子束运动100 m 距离时，RMS横向尺寸约为19 m，RMS偏转角约为112 mrad，RMS纵向尺寸约为10 m，其横向、纵向发散程度和偏转角均远大于其他3组能量电子束；随着L-shell的增大，背景磁场减小，4组能量电子束在横向发散上均有所减小，在纵向发散上0.1 keV 电子束有所减小，而其他3组变化不明显；对于0.1 keV 电子束，相比于L-shell=5时的结果，L-shell=6时其横向和纵向发散均有明显的减小。

图8 L-shell等于6时模拟结果Fig.8 Simulation resultsfor the case of L-shell = 6(B0=144.4 nT)

2.3.5 L-shell=7的模拟结果

图9所示为L-shell=7时的0.1 keV、1 keV、10 keV 和100 keV 电子束运动100 m 的RMS横向尺寸、偏转角和纵向尺寸变化情况。可以看到：0.1keV电子束运动100 m 距离时，RMS横向尺寸约为11 m，RMS偏转角约为105 mrad，RMS纵向尺寸约为10 m，其横向、纵向发散程度和偏转角均远大于其他3组能量电子束；相比于L-shell=6时的结果，L-shell=7时0.1 keV 电子束RMS横向尺寸和偏转角进一步减小，但RMS纵向尺寸几乎不变，其他3组在横向和纵向发散趋势上基本保持不变。

图9 L-shell=7时的模拟结果（B0 =91.0 nT）Fig.9 Simulation resultsfor the case of L-shell =7(B0= 91.0 nT)

2.4 RMS横向尺寸、偏转角及纵向尺寸随地磁场强度变化结果对比

图10展示了初始为Gauss和Uniform 两种分布，能量为0.1、1、10和100 keV 的电子束在不同背景磁场作用下运动100 m 时的RMS横向尺寸。0.1 keV 电子束在L-shell=5时RMS横向尺寸有最大值约为17 m，在运动60～100 m 阶段，由于背景地磁场影响，横向尺寸增长速度变快；1 keV 电子束在L-shell=4时RMS横向尺寸取得最大值约3.7 m，其他背景磁场下横向尺寸最终集中在3.2 m 左右；10 keV 电子束在L-shell=3时RMS横向尺寸有最大值约为1 m，最小值在L-shell=7时，约为0.95 m；100 keV 电子束RMS横向尺寸在L-shell 从3～7变化过程中均增长至约0.23 m，表明其受背景磁场影响较小。

图11所示为电子束运动100 m 过程中RMS偏转角的变化。能量为0.1 keV 电子束在L-shell=5时偏转最强，最终RMS偏转角约为150 mrad，Lshell为6和7时的RMS偏转角也快速增长超过100 mrad；能量为1 keV 电子束RMS偏转角最大值降低到约36 mrad，此时L-shell=4，其他L-shell下的RMS偏转角增长至31 mrad 左右；10 keV 电子束在L-shell=3时RMS偏转角增长至最大值约为10.5 mrad，表明其受背景磁场影响进一步减小，其他L-shell 下RMS偏转角集中在9.5 mrad 附近；100 keV 电子束在L-shell 变化过程中RMS偏转角最终均增长至2.4 mrad 附近。

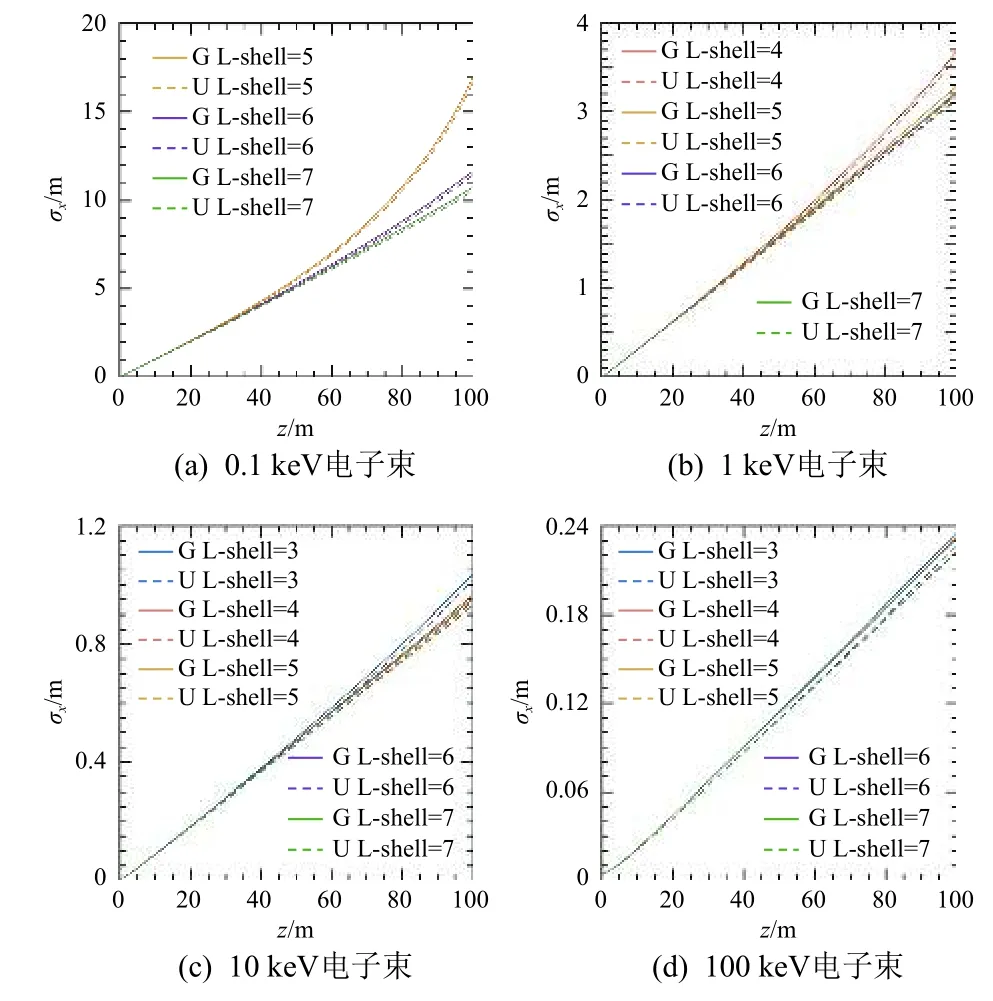
图10 电子束在地磁场运动过程中RMS横向尺寸变化结果Fig.10 Variations of transverse size of electron beam travelling through the geomagnetic field

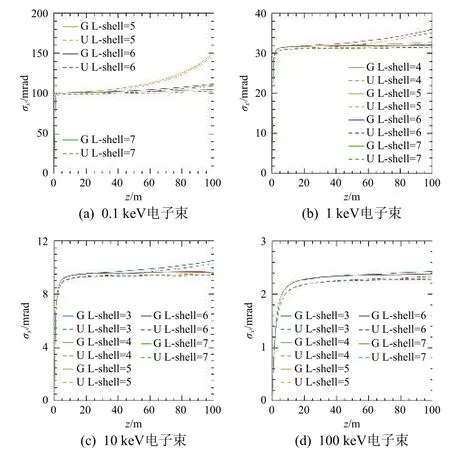
图11 电子束在地磁场运动过程中RMS偏转角变化结果Fig.11 Variations of rotation angle of electron beam travelling through the geomagnetic field

图12所示为电子束运动100 m 过程中RMS纵向尺寸的变化。0.1 keV 电子束在L-shell=5时纵向尺寸有最大值约11 m，其他磁场条件下集中在10 m 左右；1 keV、10 keV 和100 keV 电子束纵向尺寸受背景磁场影响较小，运动结束时分别集中在约3.1 m、1.1 m 和0.5 m，此时电子束纵向尺寸变化主要受电子束空间电荷效应影响。

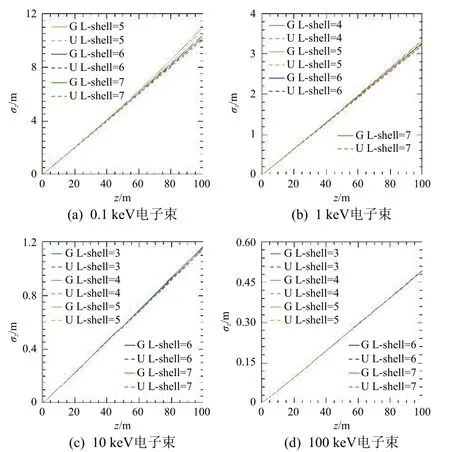
图12 电子束在地磁场运动过程中RMS纵向尺寸变化结果Fig.12 Variations of longitudinal size of electron beam travelling through the geomagnetic field

3 结束语

本文基于PIC方法建立了三维电子束的静电动力学模拟系统beamPIC程序，并研究了在地球磁场作用下电子束运动过程中由于自场和背景场的联合效应而出现的发散、拉伸和偏转现象，得到如下结论：

1）基于PIC方法的电子束自洽模型可以很好地解决带电粒子与场的耦合过程，beamPIC程序整体具有良好的可靠性。

2）电子束在空间运动传输100 m 过程中，受地球磁场和自身空间电荷效应耦合作用，会出现发散和偏转现象：背景磁场强度一定时，电子束的RMS横向尺寸、偏转角和纵向尺寸与电子束能量成负相关；电子束能量一定时，其RMS横向尺寸、偏转角与背景磁场强度成正相关；空间电子束能量＞1 keV 时，其RMS纵向尺寸在不同背景磁场条件下变化基本一致，此时电子束纵向主要由于空间电荷效应而产生发散。

上述研究结果表明，电子束结构在背景地磁场环境中的运动演化非常复杂，会同时受到束结构自身的静电力和背景磁场的洛伦兹力作用，使电子束产生横向的发散、纵向的拉伸以及绕磁力线的偏转和能量色散等多种效应，且各种效应之间往往存在复杂的耦合效应。使用粒子云算法可以对这一复杂物理过程进行精确有效的描述。

值得注意的是，在本研究中，我们假设背景空间为真空环境，而实际的空间环境中存在着背景等离子体和各种波动现象。因此在未来的研究中，我们将着重考察电子束结构在运动过程中与背景等离子体和波动的相互作用。