单相PWM直流电源直流电压波动抑制策略研究

姜晓健，宋汐瑾，郭利辉，许海波

（1.西安石油大学 电子工程学院，陕西 西安 710065；2.许昌学院 电气（机电）工程学院，河南 许昌 461000；3.河南帕沃电气科技有限公司，河南 许昌 461000）

0 引言

在电力电子技术快速发展的今天，单相PWM直流电源因具有较高的功率因数、能量可双向流动等特点，在新能源发电、直流微网、储能等方面得到广泛的应用[1-3]。

单相PWM直流电源的电压和电流工频决定了交流侧的输入功率中同时存在功率直流分量和功率二倍频分量。根据功率守恒定律，输出功率中也会存在功率二倍频分量。该谐波分量对整流器交、直流侧都会产生影响，例如，电能的质量会降低、元器件的使用寿命会缩短、系统的稳定性会降低等。为了抑制二倍频分量，一般的方法是在直流输出侧并联电解电容，且该电解电容的容值比较大。但是，容值较大的电解电容会增大系统的体积、提高系统的成本、系统的动态性能会变差。另外，电解电容抑制低频谐波电压的能力和使用寿命都是有限的[4]。文献［5-7］中滤除直流电压中的二次谐波的方法是在控制策略中采用陷波滤波器。陷波滤波器狭窄的带阻，具有一定的局限性。文献［8-10］中同样是构造了二次谐波的抑制电路，但是对于抑制电路的控制过于复杂。文献［11-13］中的控制策略基于反步法，李雅普诺夫函数的加入，使得运算量增大，准确性难以得到保证。

本文借鉴上述方法，为了减小直流侧电容的容值，在单相PWM直流电源主电路的直流母线上并联二倍频抑制电路，通过由PR控制器控制的双闭环控制策略，有效控制二倍频抑制电路中功率开关管的通断，将直流母线中电压二倍频波动转移至抑制电路的辅助电容Cr和辅助电感Lr中。

1 单相PWM直流电源二倍频抑制电路的工作原理

单相PWM直流电源二倍频抑制电路的拓扑结构如图1所示。

图1 单相PWM直流电源二倍频抑制电路

图1中，us为单相交流电压，L为交流侧电感，is为交流侧输入电流，C为直流侧电容，idc为直流侧输出电流，Udc为直流侧输出电压，iR为流过负载的电流。假设上述元器件都为理想元器件，忽略开关管的损耗，单相PWM直流电源在单位功率因数下运行[4]，令单相交流电压为：

交流侧输入电流为：

由（1）和（2）得直流电源输入功率为：

式中：U为单相交流电压us的有效值，I为交流侧输入电流is的有效值，ω为单相交流电压角频率。

由式（3）可知，单相PWM直流电源的输入功率可以看成是由直流量功率和二倍频谐波功率构成。根据功率守恒定律，单相PWM直流电源的输入功率等于输出功率，即在直流侧也会存在二倍于输入电压频率的谐波功率。

为了抑制直流侧二倍频分量，构造图1所示的单相PWM直流电源二倍频抑制电路。该二倍频抑制电路由4个开关管、1个辅助电感Lr和1个辅助电容Cr构成。其工作过程包括以下四种工作状态：（1）S5和S8导通时，辅助电感Lr和辅助电容Cr被直流母线充电。（2）S5和S8关断时，二极管D6和D7续流，二倍频抑制电路将辅助电感Lr和辅助电容Cr中储存的能量传输到直流母线。（3）S6和S7导通时，直流母线向辅助电感Lr和辅助电容Cr反向充电。（4）S6和S7关断时，二极管D5和D8续流，将能量回馈到直流母线。只要选择适当的控制策略，控制4个开关管的通断，就可以消除直流电源直流电压的二倍频波动。

交流侧电感上消耗的能量WL为：

对式（4）求导可得网侧电感L的功率PL为：

根据功率守恒定律，可得直流侧输出功率为：

式中：Po为直流侧输出直流功率，Prip为直流侧二倍频功率。

由式（6）可知，直流侧输出的直流功率Po和直流侧二倍频功率Prip为：

令二倍频抑制电路中辅助电容Cr的电压为：

式中， 为辅助电感的幅值，θ为二倍频抑制电路中电容电压与输入电压的相位差值。则流过二倍频抑制电路的电流ir可表示为：

辅助电感电压 可表示为：

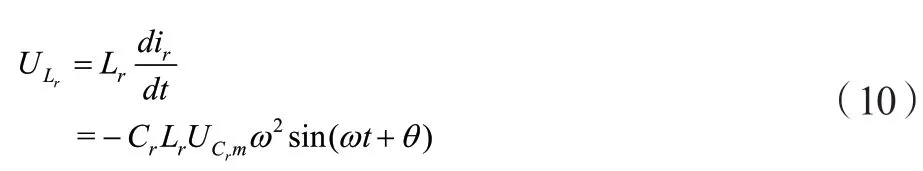
二倍频抑制电路的功率Prip可表示为：

联立式（8）、（9）、（10）和（11）并化简可得：

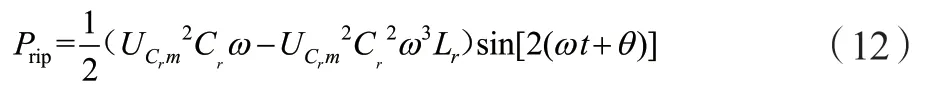
联立式（7）和式（12）可得：

由于网侧电感功率PL很小，所以在计算时可忽略。忽略后，由式（13）可得辅助电容电压幅值 为：

由相位关系可得：

解式（15）可得：

根据上述推导，只要合理设计二倍频抑制电路的参数，该电路就能有效的抑制直流电压波动。

联立式（9）、（10）和（14）可得：

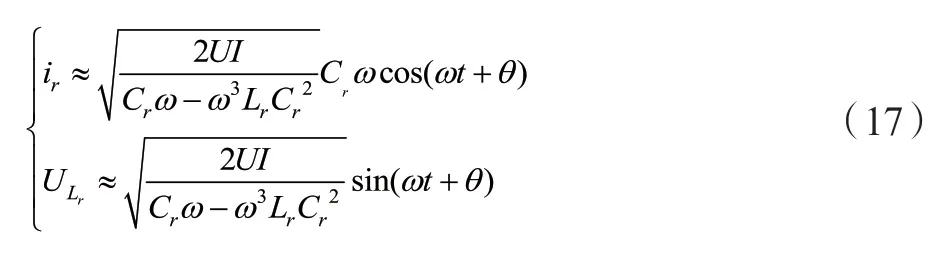
将上述数据代入式（18）可得网侧电流的有效值：

令输入电压频率f=50Hz，则角频率为ω=2πf=314rad/s。

将上述数据代入到式（14），解得辅助电容Cr的电压幅值为：

2 二倍频抑制电路的控制策略

单相PWM直流电源采用PI+PR复合控制策略，如图2所示。单相锁相环（PLL）确定参考电流相位。PI控制器控制直流母线电压，使输出为参考电流的幅值。将这个幅值与单位正弦电流信号相乘，即为给定的参考电流。最后，采用PR控制器对交流输入电流参考值进行无静差跟踪。二倍频抑制电路如图3所示。将直流侧二倍频功率有效转移至辅助电感和辅助电容中，能够有效地抑制直流侧二倍频分量。

图1中，电阻负载只吸收直流功率，而二倍频功率通过开关管传递到二倍频抑制电路的辅助电容Cr中，将辅助电容与1个小电感Lr串联，限制二倍频抑制电路中电流和电容电压的突变。

图3中的数据-0.785398为辅助电容电压与单相交流输入电压的相位差θ，143.935为辅助电容Cr的电压幅值 。

2.1 PR控制器原理

传统的双闭环控制策略中多用PI控制器，但PI控制器不能对正弦信号实现无静差跟踪，所以由此产生的稳态误差会对跟踪电流的幅值和相位造成影响。跟踪电流幅值的误差可以通过增大控制器的比例系数和增大基波频率来实现，但是无法完全消除。而相位误差则需要通过改进控制器来实现[14]。

下面给出PI控制器和PR控制器的传递函数以及在基波频率处的增益。

PI控制器的传递函数为[15]：

PI控制器在基波频率ω0处的增益为：

由式（22）可知，PI控制器在基波频率ω0处的增益是一个有限值，会使系统存在零稳态误差，且抗干扰能力不足。

PR控制器的传递函数为：

在基波频率ω0处的增益为：

由式（24）可知，PR控制器在基波频率ω0处的增益无穷大，可以消除零稳态误差的同时提高系统的抗干扰能力。

2.2 PR控制器的设计

本文使用控制变量法来分析PI、PR控制器各个参数的作用。

令kp=0，ω0=314rad/s,分析控制变量kr的值发生变化时，其对系统性能的影响。

由图4可知，增大变量kr的值，相应的增益会增大，稳定性增强，对控制器的带宽无影响。但是kr增大到一定程度就会引起谐波分量的放大，所以在满足基波处有较大增益的同时，又能具有一定的衰减性[15]。

图4 kp变化时PR控制器bode图

令kr=10，ω0=314rad/s,分析控制变量kp的值发生变化时，其对系统性能的影响。

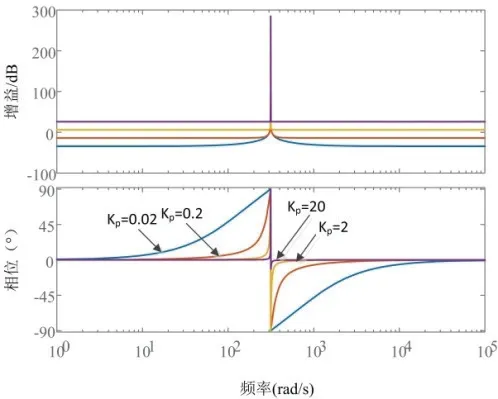
图5 kp变化时PR控制器bode图

由5图可知，增大变量kp的值，非基波频率处的增益变大，基波频率处不变，而带宽随着kp的增大而减小。所以随着kp的增大，系统的抗干扰能力逐渐增强。但是kp不能无限增大，否则会造成系统振荡。

按照上述原则设计PR控制器的参数，系统的稳定性和抗干扰性较好，系统的控制效果达到最佳。

根据本实验实际情况的需要，设计单相PWM直流电源主电路的PI控制器参数设计为：kp=0.02，kr=10.25，PR控制器参数设计为：kp=40，kr=250。二倍频抑制电路中，两个PR控制器参数均设计为：kp=5，kr=500。

3 仿真与实验

在MATLAB中搭建单相PWM整流器以及二倍频抑制电路的仿真模型，仿真模型的相关参数设置见表1。比较单相PWM直流电源在加入二倍频抑制电路前后的运行结果，仿真结果如图6和图7所示。仿真结果验证了所设计的二倍频抑制电路可以有效的抑制直流侧电压的二次谐波。

图7 满载工况施加抑制策略前后FFT对比

表1 仿真模型的参数

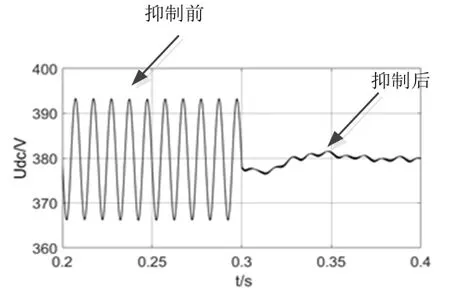
图6 满载工况施加抑制策略前后直流电压波形对比

从6图中可以看出，满载工况在0.3s前未施加抑制策略，直流侧输出电压Udc在366V-394V范围内波动。在0.35s后重新进入稳态并实施抑制策略，直流侧输出电压Udc在379V-381V范围内波动。

从图7中可以看出二倍频谐波分量明显减少，相对直流谐波含量从抑制策略加入前的3.56%减小到0.13%，表明该二倍频抑制电路对于单相PWM直流电源直流电压波动有较好的抑制作用。

为了更好的反映实际情况，在电力电子平台V2.5上验证二倍频抑制电路的有效性及正确性。控制模块采用TI公司的TMS320F28335型DSP，功率开关管采用型号为BSS126I的N沟道型MOSFET金属氧化物半导体场效应管，其他的实验参数与仿真模型参数相同。电力电子平台V2.5如图8所示。

图8 电力电子平台V2.5

如图9所示，对比抑制策略前后的实验波形，可以明显看出加入抑制策略后，直流电压Udc的波动大大减小，从抑制前的48V减小到抑制后的5V以内。

图9 抑制前后实验电压波形

4 结语

本文通过建立单相PWM直流电源的数学模型，分析了主电路工作原理及直流侧输出电压二倍频波动产生的原因，设计了二倍频抑制电路的拓扑结构及由PR控制器控制的双闭环控制策略，仿真和实验结果验证了二倍频抑制电路对直流侧输出电压中二倍频波动抑制的正确性与有效性。