考虑柔性负荷的激励型需求响应的双层优化调度

张超

（贵州创星电力科学研究院有限公司，贵州 贵阳 550002）

0 引言

随着主动配电网的迅速发展和大量的分布式电源并入配电网，使得电网的优化调度越来越趋向于复杂化，而将柔性负荷引入主动配电网的优化调度使主动配电网优化调度更具有灵活性[1]。以电动汽车、温控负荷和分布式储能为代表的柔性负荷在新一代智能电网接入的比例不断增加，柔性负荷参与需求响应一般分为价格型和激励型两类[2-3]。文献［4］构建了能够同时兼顾电能生产经济性和低碳性的含风电电热联合系统综合优化调度模型，在需求侧调度柔性负荷以实现负荷调峰。许多文献关于激励型的需求响应，提出了一些最优激励策略，并在先导实验中得到实行。文献［5-6］利用柔性负荷的经济性和互补性，提出了低电价折扣和高倍赔偿激励措施，虽然可以提高系统稳定控制和容量配置的经济性，但不足之处是低电价折扣是一种确定性计划，高倍赔偿携带高风险性，而且两者实用灵活性欠佳。文献［7］试图在用户自愿的基础上增加灵活性，提出了基于优惠券激励的需求响应（Coupon Induced Demand Response, CIDR），以优化优惠券大小来改变用户参与灵活性。同时，CIDR还具备给电力用户经济上的回扣、降低昂贵的发电资源、减少需求侧高峰期的用电负荷以及电力用户拥有是否参与的选择权。但是，由于CIDR支付给客户的优惠券折扣通常预先确定的固定值，在实际应用场景中部分无法不能满足。文献［8］设计了一种兼具弹性和自愿属性的优惠券需求响应（Customer Voluntary Demand Response, CVDR）计划，但一方面无法满足电力用户日用电需求以及在经济激励分配时存在不公平现象，另一方面没有真正体现出用户参与的弹性和自愿属性。此外，文献［9］将电网公司对用户的补偿分为容量补偿和电量补偿两个部分，容量补偿是固定的，无论用户是否被调用都支付给用户，而电量补偿则是依据用户负荷调用量的多少确定。

总的来说，大多数基于IDR的研究主要集中在负荷建模和采用所建模型来改善电力系统的运行，并且所提的激励计划在很大程度上受到参与计划的用户数量和用户意愿的影响。考虑到这一事实，本文在CVDR的研究基础上以及现代信用消费背景下，提出一种新颖的激励补偿机制——基于经济信用的激励型需求响应机制（Economy Credits Incentive Demand Response, ECIDR）。所提机制依赖于在DR期间向用户提供可参与经济信用激励计划的机会，经济信用激励大小由经济激励和信用激励两部分构成，所获取的激励可以在DR期间的任何时间段兑换成相应的电量补偿，从而以降低用户用电成本。

1 双层优化调度模型

双层优化调度模型[10-11]主要考虑含新能源光伏发电、储能蓄电池装置以及居民用户集群的可转移柔性负荷，模型响应结构如图1。

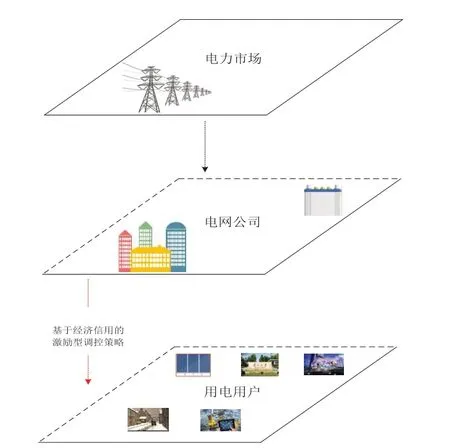
图1 双层响应结构图

1.1 经济信用激励机制

经济信用激励机制目的是鼓励用户在低谷时段增加负荷用电量，负荷高峰时段减少用电量，在保证正常用电的基础上向用户提供自我管理用电成本的机会，从经济角度分析电网公司和用户在所提策略中各自获得的收益情况。最大优点是增加用户自愿参与度的同时优化经济用电以及降低系统运行成本，属于一种信用用电。经济信用机制由经济机制和信用机制两部分够成，经济机制获取的经济激励是根据用电用户的负荷变化量、时间段以及单位激励电价来确定，采用多阶段报价曲线表示。

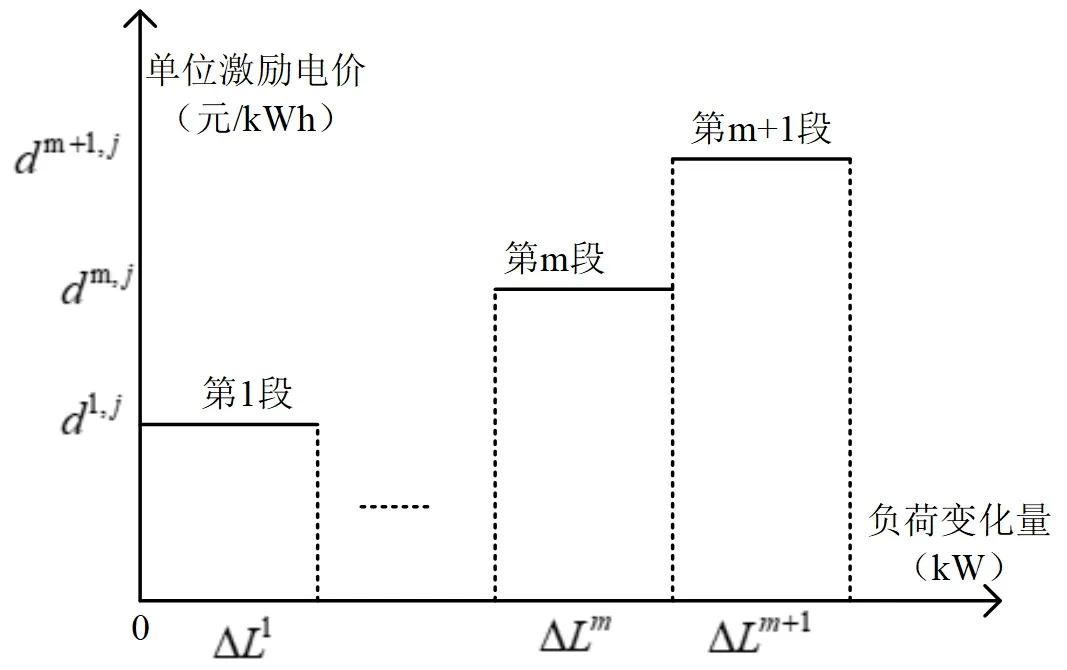
图2 激励电价报价曲线

经济机制所获得的经济激励c1表达式为

式中 为电量变化量； 为单位激励电价； 为负荷变化量对应的时间段；M为多阶段报价曲线的总分段数。

信用机制所获得的经济激励c2的获取，引用通讯积分获取思路，主要根据用户参与EC-IDR的次数评定用户用电星级指数，以次数为单位，一天仅计响应一次。如果用户每月至少参与EC-IDR计划6次则评为一星用户、至少12次评为二星级用户、至少18评次为三星用户、至少24次评为四星用户。再根据一星至四星用户分别按照当月电费支出账单金额（元）的0.001倍、0.015倍、0.002倍、0.025倍的规则回馈用户。例如某用电用户为四星客户，月份电费为2000.30元，则可获得信用激励经济50（2000.30×0.025=50.0075，向上取整为50元）。经济信用机制所获得的经济激励表达式

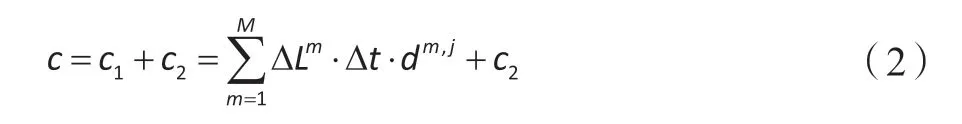
经济信用激励获取是在参与DR事件期间，由电网公司向用电用户提供可以参与到EC-IDR的机会且选择参与才能获取。本文设计的经济信用机制激励不是直接以经济形式补偿，通过在DR事件期间兑换成相应的电量补偿，最终形成电量激励补偿。

1.2 双层优化模型

双层优化模型主要考虑储能蓄电池装置、分布式光伏发电、居民负荷中的基本不变负荷和可转移柔性负荷，所建模型为上层电网公司收益最大化、下层为用户电费支出最小化的DR双层优化模型，模型结构如图 3，电网公司通过智能电表收集用户负荷设备用电数据和传送激励信号到调度控制器上。当电网公司的零售电价低于向电力市场的购电电价时，就向用户提供获取激励补偿的机会，吸引用户改变可转移柔性负荷设备的用电时段来改善电网公司在此时段的经济亏损。而用户根据电网公司提供的激励补偿计划来优化自身的可转移柔性负荷的大小。EC-IDR激励计划的全局最优解是电网公司收益最大化时对应的经济信用激励大小和柔性负荷功率变化

图3 EI-IDR双层调度模

1.2.1 可转移柔性负荷模型

居民用户中的可转移柔性负荷，典型的有洗衣机、热水器、电饭煲和电动汽车等，该类负荷的开关时间灵活可控，根据DR不同时段的电价，调整开启时间来对其用电时段转移，以此来达到居民用户用电成本减小化和可转移负荷移峰填谷的目的。

（1）洗衣机、电饭煲类可转移负荷。洗衣机、电饭锅类可转移柔性负荷的特点主要是负荷设备开启时间较为灵活。根据DR不同时段的电价激励情况，该类负荷可通过改变负荷设备开启时间来对其用电时段进行转移，以此达到减小居民用电成本。利用与控制终端进行TCP/IP协议和ZigBee协议的通信方式来实现[12]，模型表示为

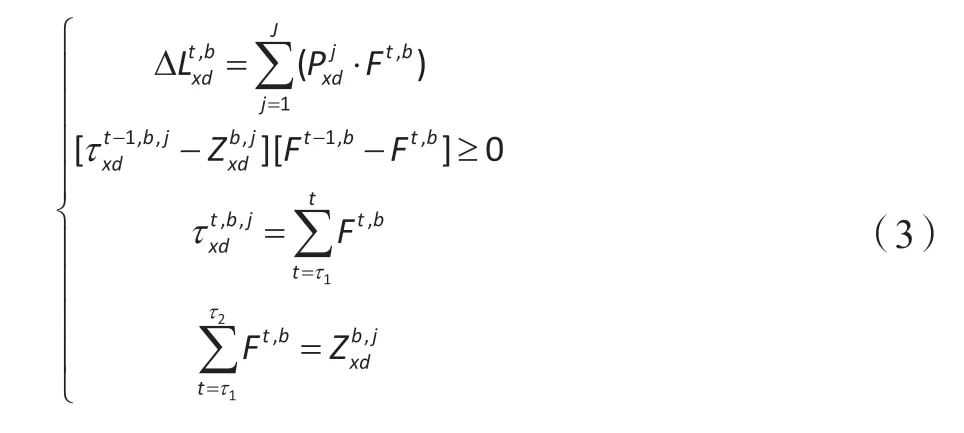
（2）电动汽车可转移负荷。电动汽车可转移负荷相对于洗衣机、电饭煲类可转移负荷来说比较特殊，主要因为在充电时段内充电，充电功率可灵活监测控制，只需要确保充电结束时满足用户需求即可。电动汽车可转移负荷的数学模型表示为：

（3）蓄电池模型。储能电池是未来家庭常备的可调度设备，因其充放电能力强，能够有效的进行负荷转移和进行负荷需求响应。储能电池的荷电状态（State of Charge，SOC）和充放电功率P的关系表示为：

1.2.2 上层电网公司优化模型

假设t时刻，电网公司向用户提供参与EC-IDR激励补偿的机会后，电网公司向电力市场的购电电量是 （单位：kWh）且购电单价为（单位：元/kWh），采用峰平谷电价购买；下层负荷端在t时刻线路l的总电量负荷是（单位：kW），时段总负荷变化量是电网公司对用户的零售电价为采用恒价零售；电网公司能够承担给用户的电量补偿所带来的经济损失是（单位：元），是关于 的不连续分段函数，表达式见1.2.3小节；上层模型的目标函数是电网公司收益最大化，表达式为

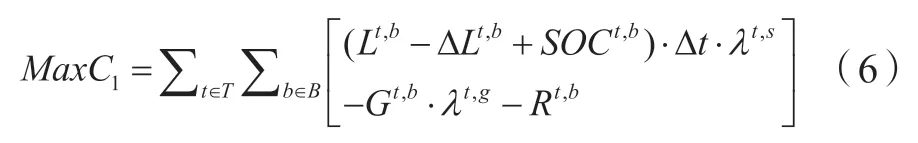
式中T为优化周期；B为系统母线总数； 为蓄电池荷电状态。

约束条件：

（1）在t时刻节点b=1,2,3, ，B的功率平衡约束。

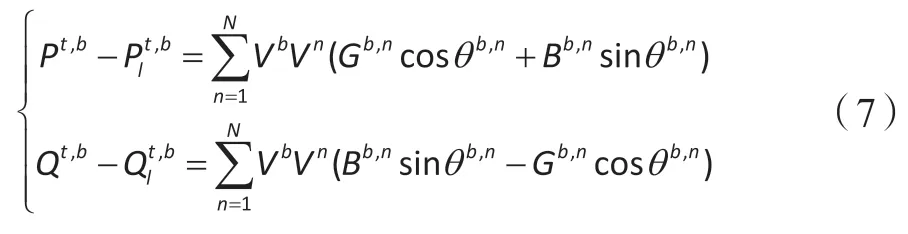
（2）节点电压约束。t时刻节点的电压波动范围限制在额定电压的±5%之内。

（3）线路电流约束。为了确保线路安全运行，线路l电流需限制在最大电流之内。

（4）电网公司向电力市场的购电电量上下限约束，电量激励补偿所带来的经济损失上下限约束。

在医院药房工作的所有工作人员都需要拥有自己的编码和登录密码，在输入自己的编码和密码之后才能够进入到药房的管理系统当中，进行各项操作[4]。每一次登录和操作，系统都要准确的记录工作人员对于哪一种药物采取的哪一种操作形式，才能够完善医院的药品质量管理工作。

（5）蓄电池的充放电功率约束、容量约束以及单位时间内充放电功率约束。为了最大化利用蓄电池的调度作用，蓄电池初始容量和结束时容量相等。

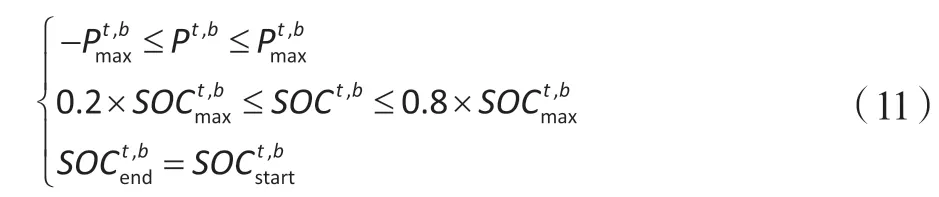
1.2.3 下层用电用户优化模型

下层模型是用户根据电网公司提供的经济信用激励补偿大小，改变负荷用电量，获取经济信用激励来换取电量补偿，从而使自身用电成本得到改善。下层目标函数以优化周期 内用户电费支出最小化，表达式为：

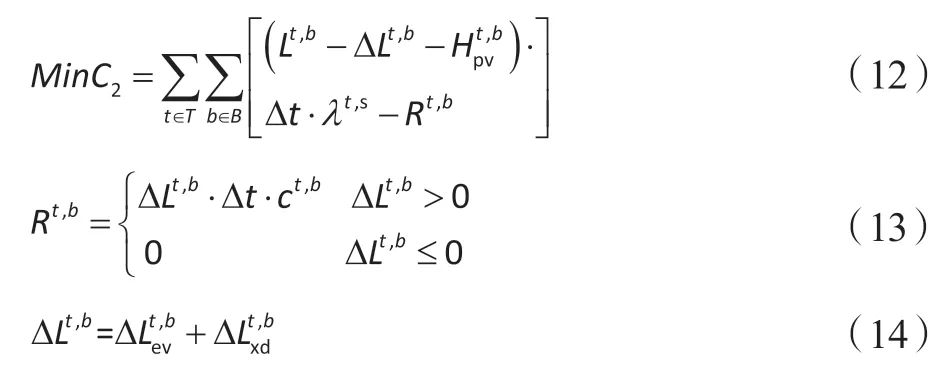
约束条件：

（1）经济信用激励约束。为了保证电网公司有足够影响力引导用户的用电行为，以及具备一定的盈利空间，对经济信用激励采取上限约束。

（3）电动汽车可转移负荷在运行周期完成后满足用户充电需求。

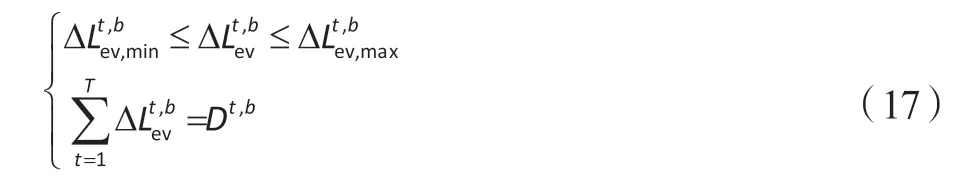
（4）光伏发电量上、下限约束。

式中 为光伏发电量上限。

1.3 模型求解

通过引入（Karush-Kunhn-Tucker，KKT）最优条件，将原双层优化模型等效转换成单层优化模型，实现原有问题解耦[13]。下层优化对应的KKT问题模型如下：

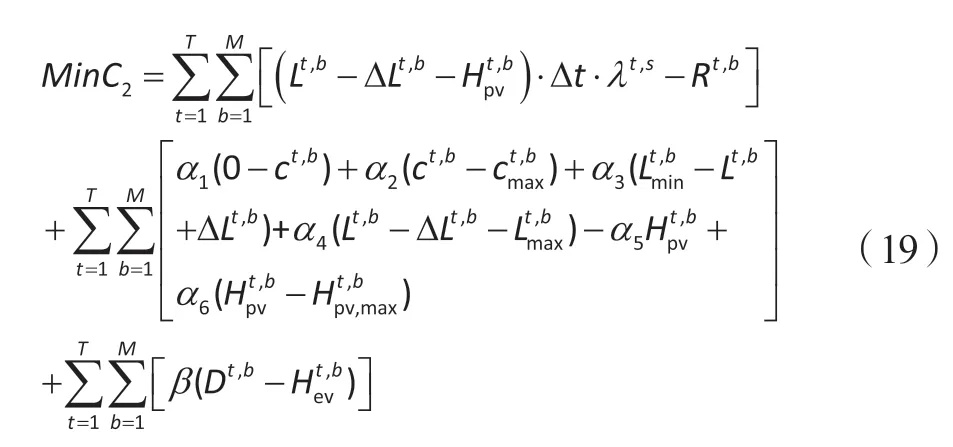
KKT最优条件：

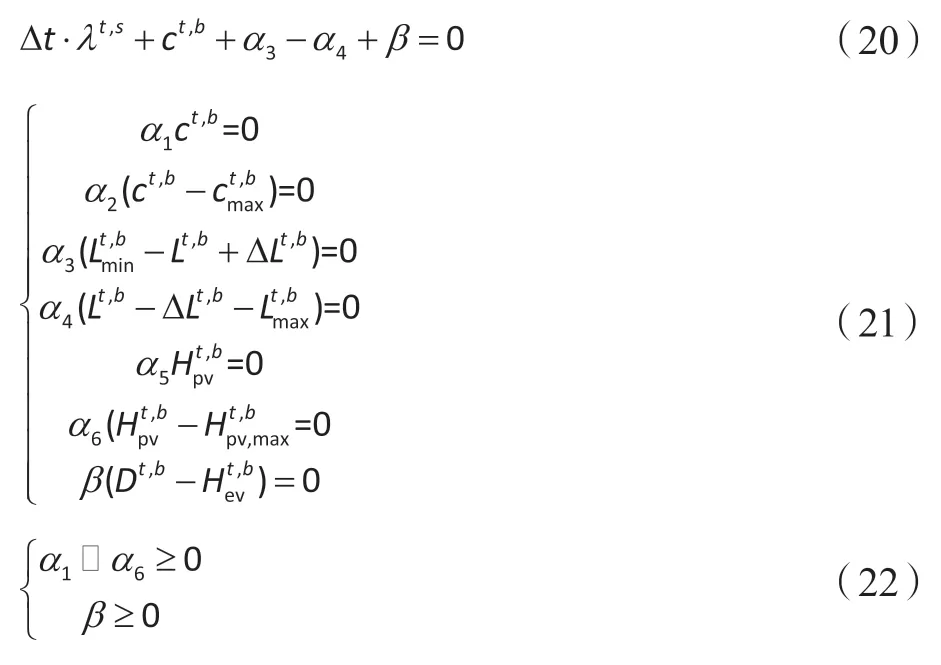
2 改进粒子群优化算法

2.1 基本粒子群算法

社会心理学家肯尼迪和电气工程师埃伯哈特于1995年在美国首次提出粒子群算法（Partical Swarm Optimization，PSO），是一种基于Swarm Intelligence的优化方法。PSO在分布式电源的选址定容问题、柔以性负荷调度、需求侧响应、配电网系统的故障重构问题以及系统的最优潮流计算问题等[14-15]。基本PSO的速度和位置更新公式如下：

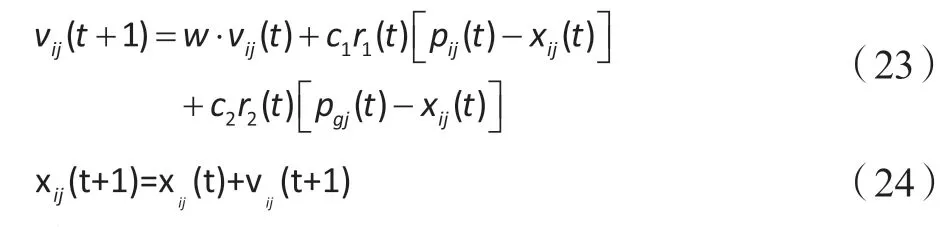
式中 是惯性权重；和 为学习因子；和 为[0，1]范围内的均匀随机数；表示粒子搜索速度限制，是可以设定的常数。惯性权重影响算法性能，较大增强全局搜索能力，较小增强局部搜索能力。

本文利用惯性权重 动态特征，使用一种带自适应变异的粒子群优化算法（Particle Swarm Optimization algorithm with Adaptive Mutation，PSO-AM）求解模型。首先，利用的动态调整方式来改善算法的搜索效率，在算法迭代的早期按照先增大、后期逐渐减小的非线性变化方式，使算法在前期的搜寻区域能够进行精确局部搜索，从而改善算法的收敛速度，以获得更好的求解效率。的调整公式为：

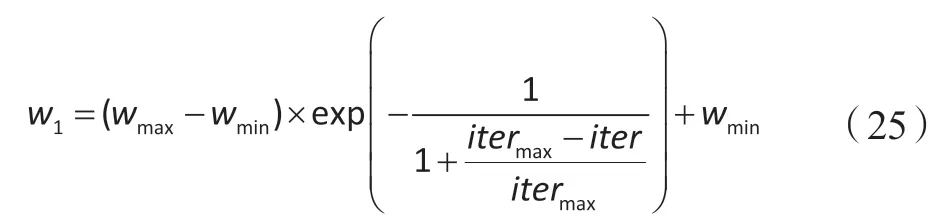
其次，为了显著PSO-AM算法的优越性，本文还分别利用线性递减的惯性权重粒子群算法和收缩因子PSO算法依次求解模型，线性递减惯性权重的调整公式为：

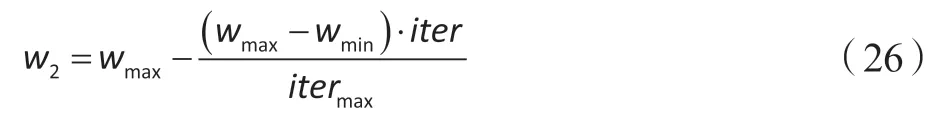
收缩因子PSO算法速度更新公式为

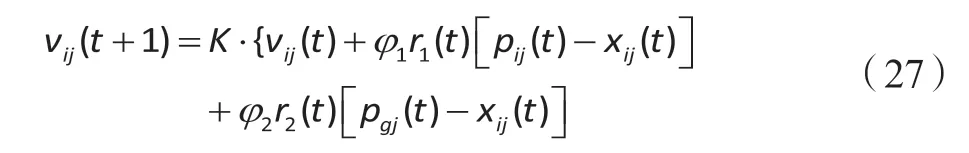
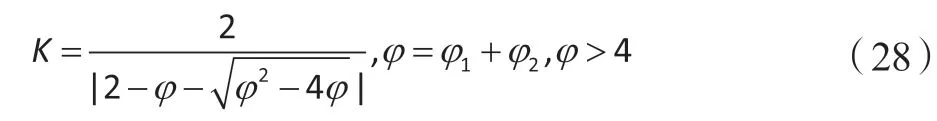
2.2 初始化编码

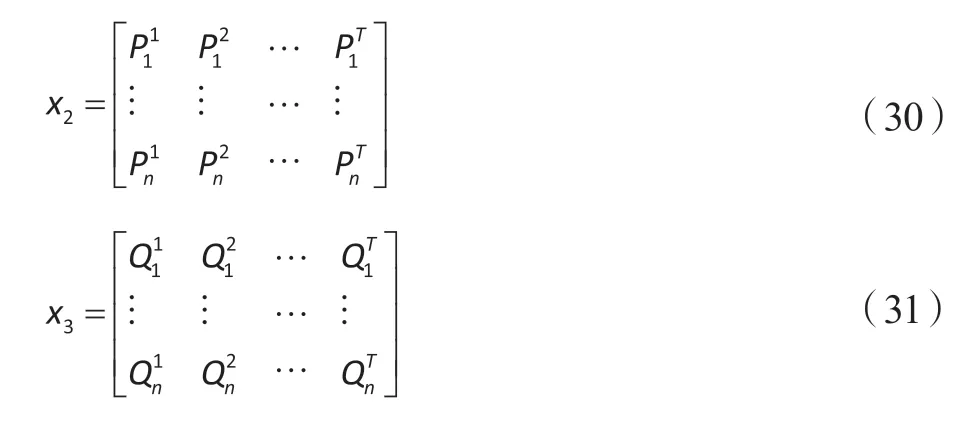
在EC-IDR激励补偿计划中，优化连续变量有经济信用激励大小、蓄电池功率变化、柔性负荷功率变化。本文对每个粒子的分布式电源和柔性负荷分开编码，连续变量有光伏发电出力、储能蓄电池功率变化、电动汽车可转移负荷、洗衣机和电饭煲类可转移负荷，用 表示为式中为光伏发电出力；为蓄电池功率变化；为电动汽车可转移负荷；为洗衣机可转移负荷为电饭煲可转移负荷

联络线有功功率变化用 表示，无功功率变化用 表示，表达式如下

2.3 约束条件处理

在基于经济信用机制的激励型DR双层优化调度模型中，对决策变量取值范围约束（光伏发电出力约束、可转移柔性负荷约束、蓄电池充放电功率约束、经济信用激励约束、负荷电量约束）采用粒子初始值来限制范围，如果有溢出边界则取边界值；对不等式约束和等式约束采用偏移度函数处理，假设有个不等式约束个等式约束。

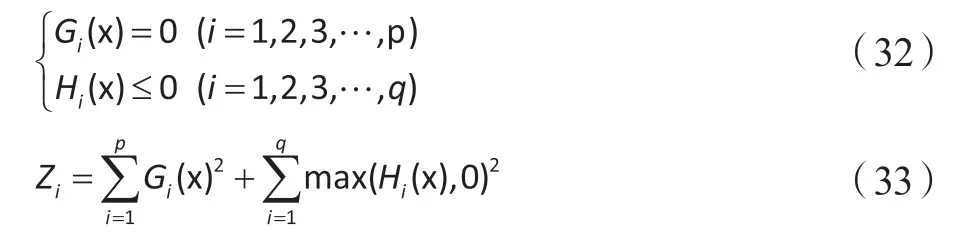
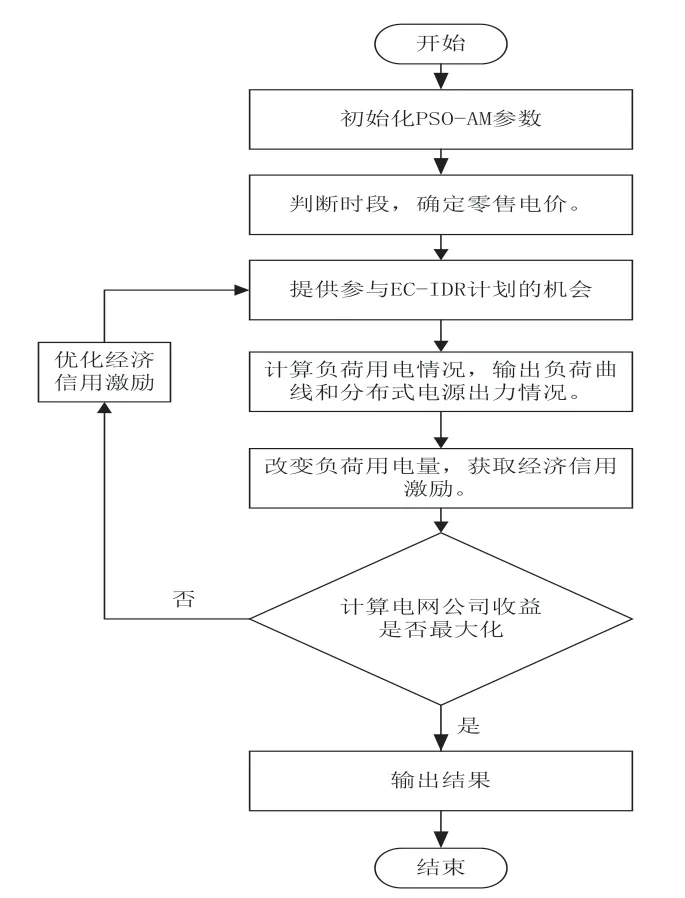
图4 EC-IDR优化流程图

3 算例仿真验证

本文采用3节点配电网系统对居民用户配电网进行仿真分析，基于电网公司和用户的EC-IDR双层优化模型采用PSO-AM算法优化求解。含蓄电池、光伏发电和居民用户集群的3节点配电网结构如，其中光伏发电接在居民用户端，使用权利属于居民用户光伏；蓄电池接在调度控制器上，调度权利归属电网公司，蓄电池最大容量为100kWh。

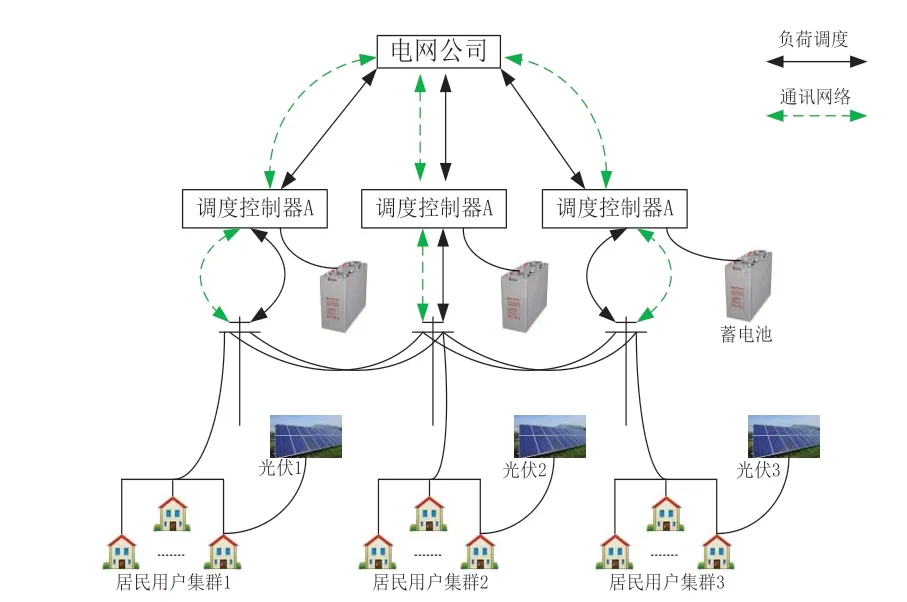
图5 3节点配电网结构图

3.1 参数设置

（1）光伏预测出力曲线、电网公司购电电价和零售电价。遵循峰平谷时段划分原则，设置谷时段为02:00-07:00，平时段为08:00-10:00、14:00-17:00、23:00-01:00，峰时段为11:00-13:00、18:00-22:00。电网公司向电力市场的购电电价采用分时段的峰平谷电价（平时段电价0.46元/kWh，谷时段电价0.38元/kWh，峰时段电价0.66元/kWh）。电网公司对用户的零售电价为0.55元/kWh。光伏预测出力和售电公司的购电价与零售电价如图 6和图 7。

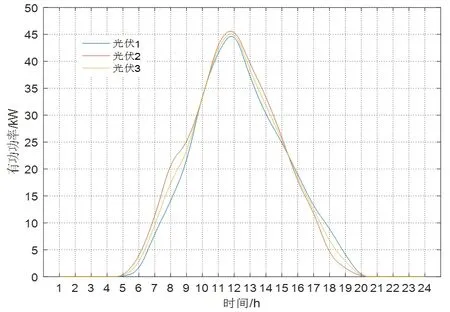
图6 光伏发电预测出力

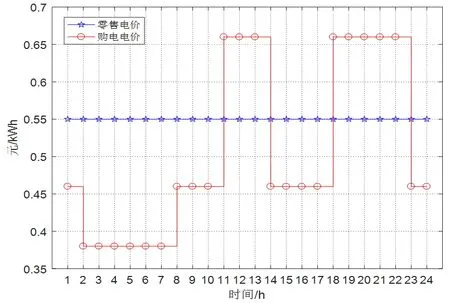
图7 售电公司的购电电价与零售电价

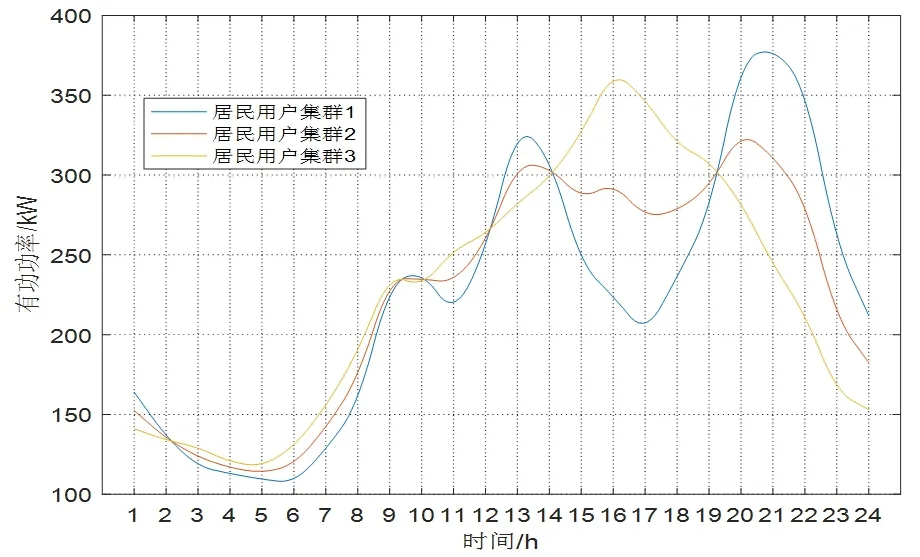
图 8 用户集群1、集群2、集群3的其他居民负荷

（2）可转移柔性负荷。居民用户集群中洗衣机和电饭煲的数量分别均为100，洗衣机额定功率为0.6kW，每次启动后的运行周期为1h，用户定义开启时段03:00~08:00，禁用时段19:00~22:00；电饭煲额定功率为1.5kW，每次启动后的运行周期为2h，用户定义运行时段（开启时段15:00~17:00，禁用时段19:00~21:00）。

电动汽车均为100辆，但居民用户集群1、集群2、集群3的电池容量分别为24kW、36kW和48kW，充电功率极限分别为6 kW、8 kW、10kW。

（3）除可转移柔性负荷外的其他居民负荷。

除电动汽车、洗衣机和电饭煲三种可转移柔性负荷外居民用户集群1、集群2、集群3的其他居民负荷如。

3.2 仿真结果分析

（1）无EC-IDR激励计划时对公司和用户的影响。给出了没有EC-IDR计划时，电网公司和用户用电在19:00-21:00时段的收益和支出情况。由可知，电网公司在该时段向电力市场的购电支出高于向用户的售电收益，处于经济亏损状态。所以，此时段内用户可以积极参与到EC-IDR中，将可转移的柔性负荷设备最大化减少用电来获取对应的经济信用补偿。

表1 无EC-IDR时公司收益和用户日支出

（2）有EC-IDR激励补偿计划时对用户的影响。以居民用户集群3为例来分析有EC-IDR激励计划时对公司和用户的影响。可转移柔性负荷参与DR优化后的结果如图9，在参与EC-IDR激励计划后，增加了设备在低电价时间段的负荷用电量，在峰值电价时段的峰值负荷也有所削减下降。图10为居民用户集群3在参与EC-IDR激励计划前后的负荷曲线对比情况。由图10可知，用户参与EC-IDR响应后，总负荷曲线最大功率由706.30kW下降到517.45kW，低电价时段负荷曲线最小功率117.35kW增加到350.78kW，总体呈现出削峰填谷的效果，说明了模型的合理性。

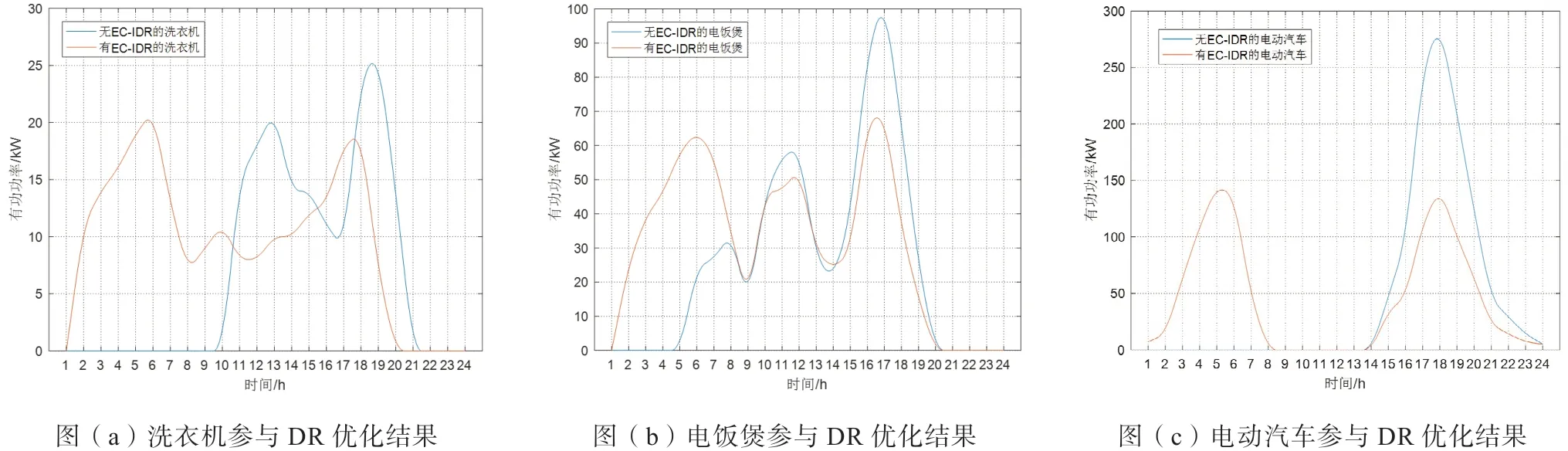
图9 用户集群3中可转移柔性负荷优化结果

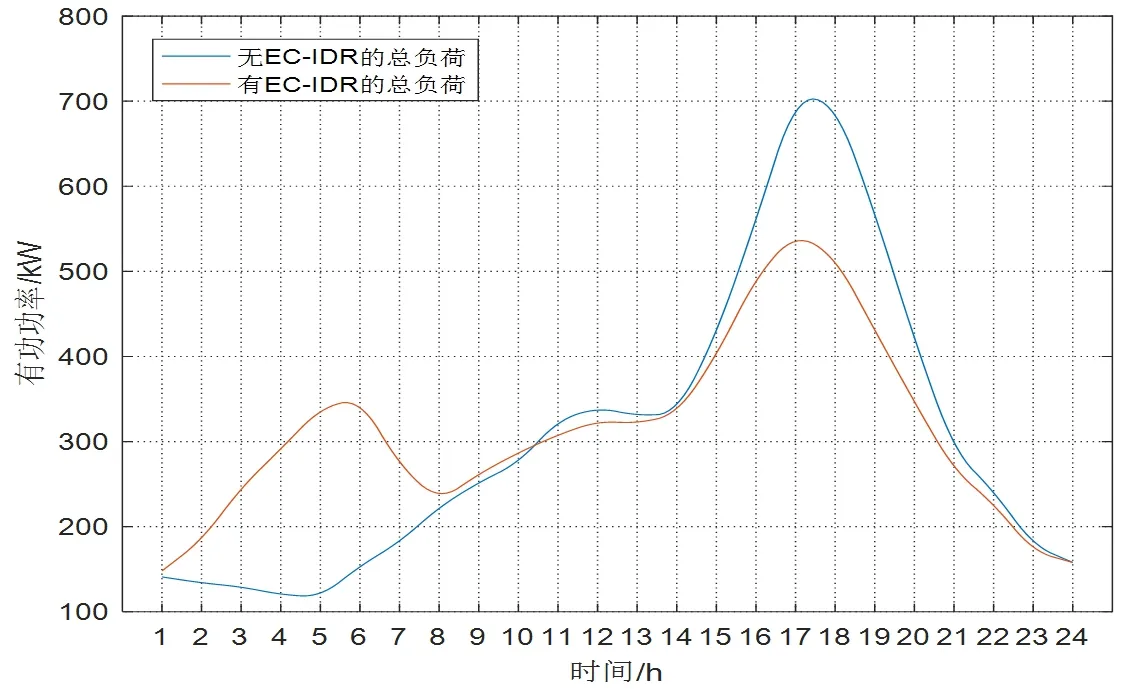
图10 用户集群3参与DR优化后总负荷曲线

（3）有EC-IDR激励计划时对电网公司的影响。优化后蓄电池容量的变化和控制器A、B、C在19:00-21:00时段的负荷变化情况如图11。由图11所知，蓄电池在低电价时段充电，峰值电价时段放电，平价时段选择性充放电，满足约束条件和功能需求。控制器A上的居民用户集群1在19:00、20:00、21:00时段负荷削减量分别为138.96 kW、73.90 kW、22.87 kW，控制器B、C所控制的居民用户集群2、3也在该时段呈现出用电负荷量下降，改善了电网公司没有EC-IDR激励计划时的经济亏损状态。

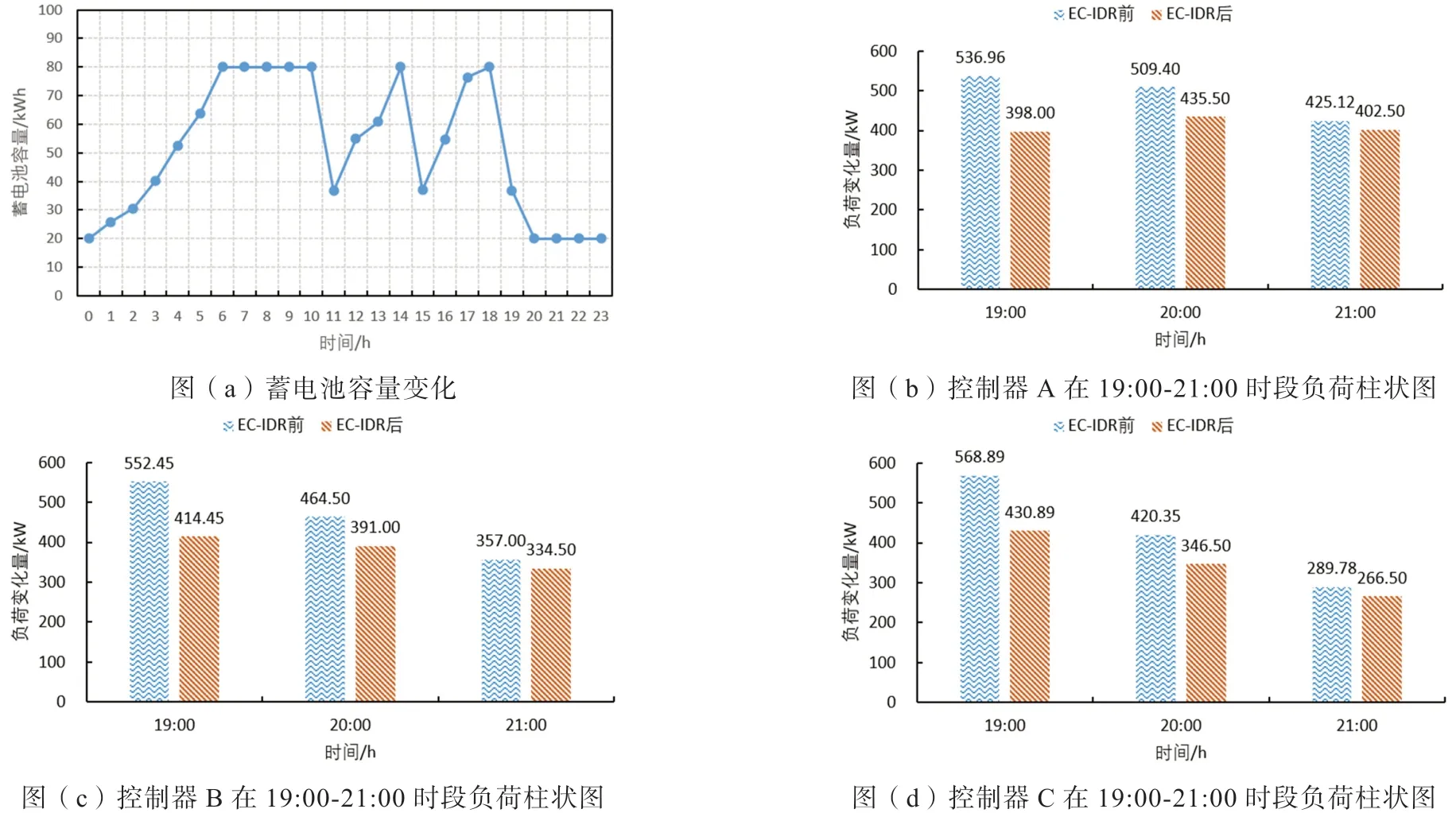
图11 蓄电池功率变化和控制器在19:00-21:00时段的负荷柱状图

（4）系统总负荷变化。图12给出了3节点配网系统的有无EC-IDR激励计划的系统负荷日需求曲线变化情况，从图 12中可知，在参与EC-IDR激励计划后，系统峰值负荷有所削减、低谷负荷有所增加，达到了削峰填谷的效

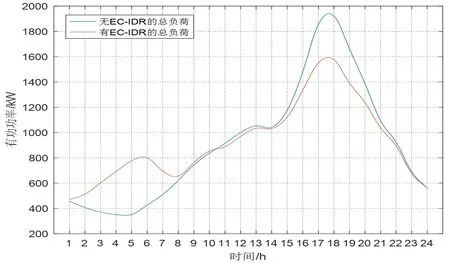
图12 3节点配网系统总负荷变化情况

果，从而验证了模型的有效性和可行性。电网公司从优化前的总收益12017.93元增加到优化后总收益12182.38元，说明了模型的经济性。

（5）经济信用激励的变化。本文仿真优化周期仅为24h，而信用激励 的获取是根据用户参与EC-IDR的次数且一天最多累计一次，达不到每月至少6次的最低标准，所以 在此为0，但是在长期调度计划中，信用激励 是经济信用激励机制不可或缺、不能忽略的组成部分。经济激励 是根据负荷DR变化量的多少来获取。负荷变化量和经济信用激励的变化如图13。从图13中可知，系统负荷在峰值电价时段最大负荷减少量为362.47kW，低谷电价时段最大负荷增加量为444.62kW，用户可获得激励最大约为14.48元，最小为0元。

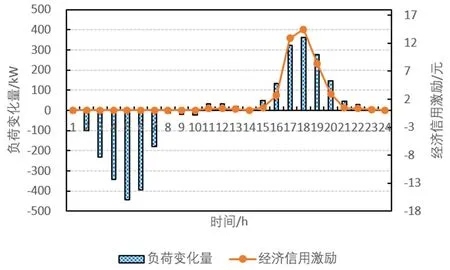
图13 负荷变化量和经济信用激励的变化

3.3 算法性能对比

为了验证本文选取的的PSO-AM算法的优越性，本文还选取了线性递减惯性权重粒子群算法、收缩因子粒子群算法对所建模型均求解20次，取计算结果的均值，3种算法的收敛曲线如图14。由图14可知，3种算法中PSOAM算法的迭代次数最少，与线性递减PSO算法和收缩因子PSO算法相比，全局搜索能力更强、收敛性更好且不易产生局部最优解问题，优越性显著。

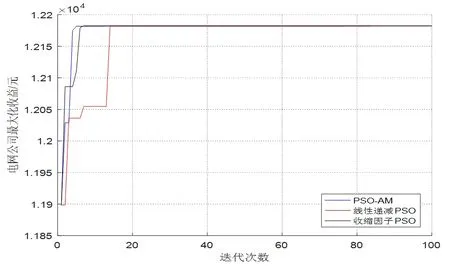
图14 三种粒子群算法收敛过程

4 结语

本文在低电价折扣与高倍赔偿、基于优惠券激励的需求响应和一种兼具弹性和自愿属性的优惠券需求响应等的激励型需求响应的研究基础上，提出了一种新颖的激励补偿计划——EC-IDR调度计划。首先，建立了包含分布式能源发电、可转移柔性线负荷、储能蓄电池的“源-荷-储”DR双层优化调度模型，上层为电网公司的收益最大化，下层为用电用户电费支出最小化。其次，利用PSO算法惯性权重的动态调整特征，采用了一种自适应的非线性递减的惯性权重PSO-AM算法求解模型。最后，引用改进的IEEE3节点配电网系统仿真分析所设计的ECIDR激励补偿计划，仿真结果说明在降低用户用电成本的同时，还能优化电网公司的收益情况，起到了降低系统运行经济成本的效果，验证了模型的合理性和有效性。