岩体地质强度指标(GSI)特征分析
2021-07-12虞金林
虞金林
(中国建筑材料工业地质勘查中心江苏总队,江苏 南京 211135)
0 引言
Hoek-Brown 强度准则是Hoek 和 Brown 在基于Griffith 强度理论以及对大量岩石三轴试验和现场岩体试验成果的分析,于1980 年提出。
广义的Hoek-Brown 准则还引进了地质强度指标(GSI)和岩体扰动系数(D)的概念,将岩体分级与物理指标参数有效地结合起来。
1 GSI 值定量化方法
地质强度指标是E. Hoek 提出的一种围岩分级系统,GSI 的取值直接与岩体力学参数相联系,因此GSI 围岩分级与Hoek-Brown 强度准则的联合使用在工程实践中更具有可操作性,能够方便、及时、准确地反映岩体的实际情况。
通过充填程度Rf、风化程度Rw与粗糙度Rr之和确定GSI 体系中结构表面条件SCR, 可参见Sonmez[1]等的研究确定取值评分表,见表1。
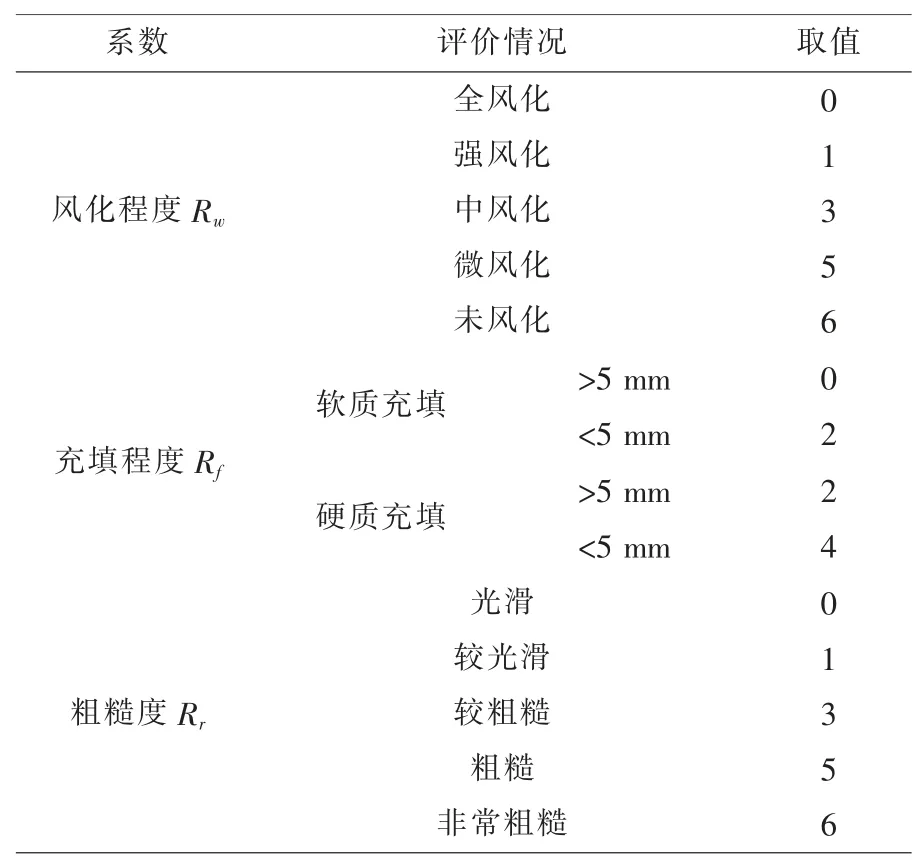
表1 结构(节理)表面条件(SCR)评分
可量化结构表面特征, 将结构表面条件SCR(0~18)分为 5 个等级。
GSI 体系中岩体结构等级SR 的计算公式如式(1~3)所示:
当岩体为块状或完整结构(I/M)时,有:
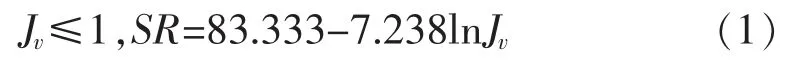
当岩体为散体结构(D)、碎裂结构/扰动/裂缝(B/D/S)、镶嵌结构(VB)、块状结构(B)时,有:

当岩体为层状/剪切带(L/Sh)时,有:

GSI 体系中根据粗糙度Rr、 风化程度Rw与充填程度Rf之和确定了结构表面条件SCR, 基于对岩体结构特征进行区间值量化需采用SCR、SR,则在岩体三维节理面网络基础上得到岩体结构等级SR 和岩体体积节理数Jv。 相关GSI 定量化表格如图1 所示。
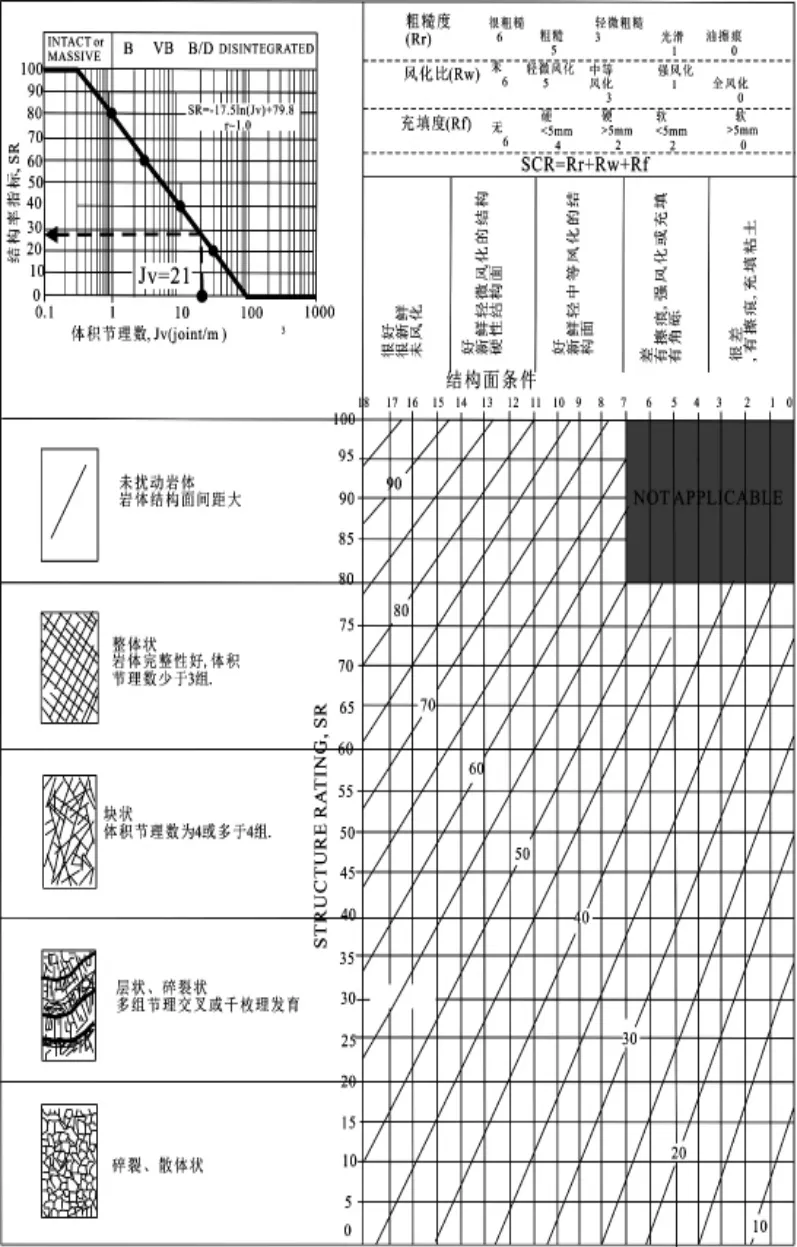
图1 改进的GSI 定量化
Hoek-Brown 强度准则中岩体力学参数取值对GSI 的取值很敏感[2],需要对GSI 的取值做到更加量化和精准。 RMR 是国际常用的岩体分级方法,其数值与[BQ]等具有一定的关系,而Hoek 等通过将GSI与RMR 联系起来, 使得GSI 的取值具有了普遍适用性。 RMR 估算 GSI 的具体表达如式(4)所示[3]:

RMR 的值可以用现场岩体特征根据RMR 分级方法进行计算,也可以根据已知的[BQ]进行换算。 大量的实测资料统计分析表明,[BQ]值与RMR值呈线性关系[4],具体使用时可采用拟合的关系如式(5)所示:

2 实例分析
根据徐州市铜山区柳泉镇杨山研究区边坡坡向,边坡类型大致分为五段,每段岩体中的结构面选取相应的层面及共轭节理面作为主控结构面进行分析。 岩体结构面间距总体上为70~100 cm,岩层厚度以中厚层为主,且岩体结构面一般处于闭合状态,无充填,结合较好。因此将岩体定性为块状或厚层状结构,岩体的完整程度应为较完整状态。
杨山五段边坡岩体的GSI 值采用定性与定量相结合的方法。 根据现场地质调查,每段边坡岩体均发育有结构面,其中以节理面居多。 本研究利用SCR、SR 对岩体结构特征进行区间值量化,通过改进的GSI 定量化表格确定GSI 值, 对比采用RMR值间接计算GSI 值, 结果见表2, 计算所得的GSI值基本均在通过GSI 定量化表格所确定的GSI 值区间范围内,这表明两种方法分析结果是一致的。
利用对应GSI 量化表用插值法确定GSI 主要依据野外岩体露头的观察和测量,然后对应GSI 量化表用插值法取值,属于直接法确定GSI。 这种方法虽简单快速、使用方便,但却具有很大的主观性和经验性, 且所得值具有一定的区间性, 不利于GSI 系统的普遍使用。 对比GSI 定量化表取值,采用RMR 值间接计算得到GSI 值指标是确定的、唯一的,方便了岩体稳定评价中参数的选取,对分析边坡稳定性以及后续开挖方案设计具有重要的参考意义。
3 GSI 值修正方法
GSI 值的一种表现形式是利用RMR 值, 在边坡开挖中,要考虑地下水和结构面产状对其产生的影响基础上来进行RMR 的取值。
岩体与节理面的蚀变作用和风化作用及地下水对岩体力学性质弱化作用等,对岩体力学性质的影响存在不同的差异。

表2 GSI 值确定法对比
黄达[5-6]等提出了结构面产状修正评分表,该表针对RMR 体系中结构面产状及其分类进行评分,见表3,α 为边坡走向与节理组走向的夹角;β 为节理组倾角。 非常有利时R1=0,非常不利时R1=15。
地下水对岩体力学性质的影响按照地下水的影响没有时R2=0,很大时R2=15,见表4。

表3 结构面产状修正评分

表4 地下水影响修正评分
修正参数Jm是根据表3、4 对现场岩体进行评分所求之和。 GSI 值的修正式如式(6)所示。
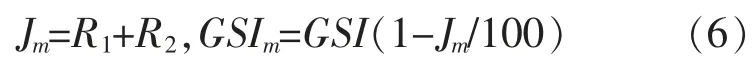
杨山五段边坡岩体的GSI 值根据GSI 值修正方法进行了修正,依据水文地质条件所得地下水修正评分值R2与通过结构面产状计算各岩体的结构面产状修正评分值R1相结合。 计算结果见表5。
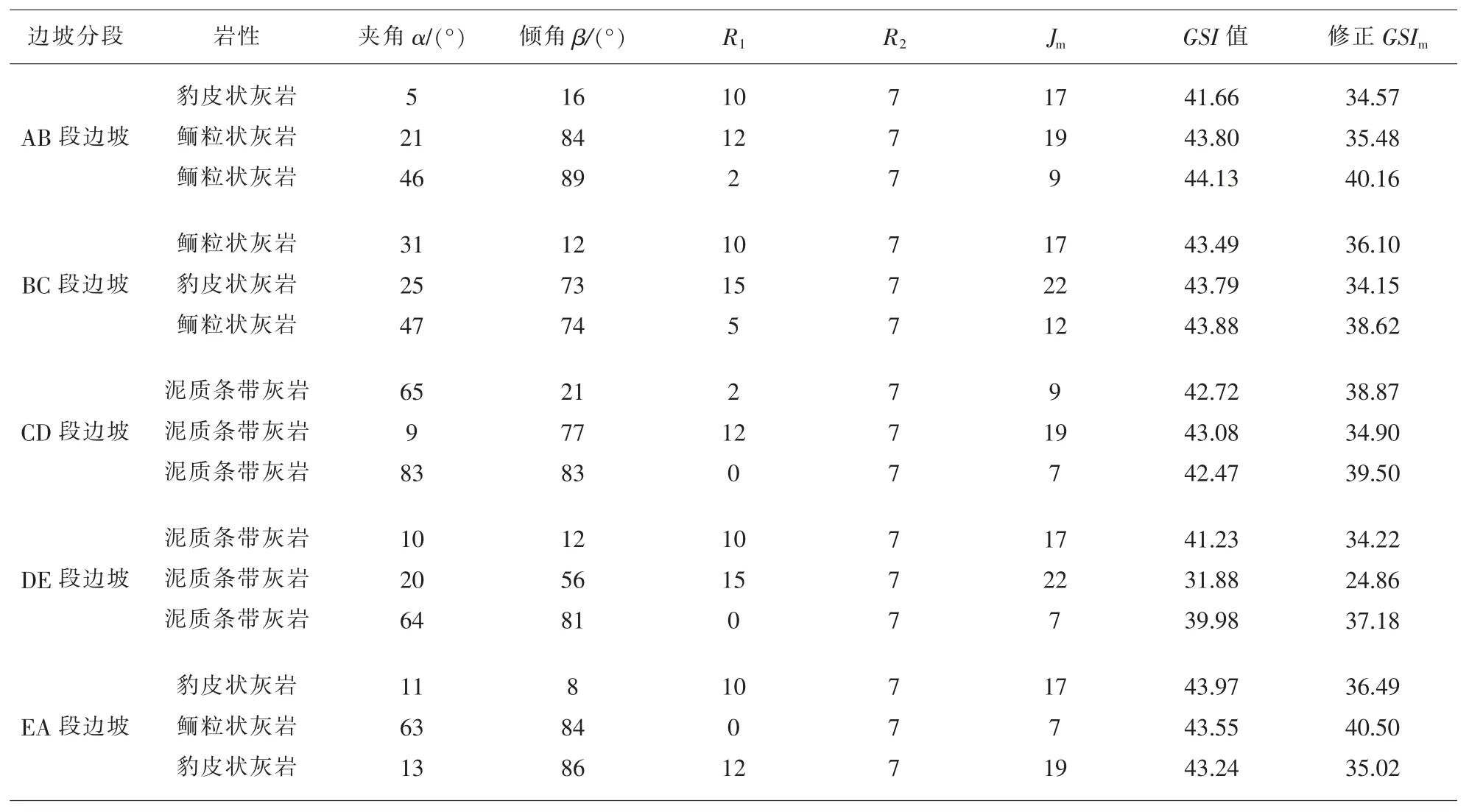
表5 岩体的GSI 修正评分值
根据表5 可知,受结构面产状及地下水情况的影响, 修正后的GSI 值比正常的GSI 值减小了7%~22%不等。
4 岩体力学参数确定
Hoek-Brown 准则下的岩体强度参数的取值除了对GSI 的确定, 还有对均质岩块指标mi和扰动系数D 的确定。 mi的取值与岩块的种类和结构面粗糙程度性质有关,Rotlab 软件中给出了mi的确定方法,表6 列出了部分相关岩体mi的取值范围。

表6 常见岩块的岩石指标mi 的经验取值
扰动系数D 的取值与爆破以及应力释放的程度有关,重载爆破破坏和覆岩卸压引起的应力解除都会引起岩体的扰动,不同坡度(平面内)产生的侧向约束对其扰动程度也有影响。 扰动系数D 的取值对岩体力学参数的确定具有很大的影响。
杨山边坡岩体在开挖中主要由生产爆破加机械开挖的方式,局部区域爆破时所造成的破坏能延伸2~3 m,因此边坡岩体扰动系数建议取值为0.8。
通过将Hoek-Brown 强度准则和Mohr-Coulomb 强度准则进行数据拟合,使在 σt<σ3<σ′3max范围内, 两个强度准则所对应的曲线覆盖面积相等,如图2 所示,最后得到基于Mohr-Coulomb 准则的等效参数。

图2 计算模型示意
Mohr-Coulomb 准则下岩体的物理力学参数都可以通过Hoek-Brown 准则来转换,RocLab 软件提供了一个方便的计算途径, 不仅可以将Hoek-Brown 准则下的参数直接转换为常用的Mohr-Coulomb 准则下的岩体力学参数,而且可以瞬时在σ3-σ1坐标系中绘出两种强度准则的岩体破坏包络线。 根据相关Hoek-Brown 准则的岩体力学参数数据,利用RocLab 软件可以计算出杨山边坡各地层分层Mohr-Coulomb 准则下的岩体力学性质指标。 为了方便GSI 法与BQ 工程岩体分级法的对比,现将两种方法所确定的结果归纳于表7。

表7 研究区边坡岩体力学参数值
根据GSI 法计算结果, 各分层岩体基本力学参数指标c' 值基本都处于BQ 工程岩体分级法所给出的取值区间内,但φ 值均处于BQ 工程岩体分级法所给的取值区间之外。 这主要是该区域岩体裂隙较发育,且裂隙内多为砂泥质充填,导致岩体地质强度指标GSI 值偏低, 使得岩体力学指标值与BQ 工程岩体分级法的区间值有所不同。整体上看,GSI 法确定的岩体力学参数指标很好地反映了该边坡岩体的物理力学性质。相比于BQ 工程岩体分级法所给的取值区间,GSI 法计算得到的指标值是确定的、唯一的,可以较为便利地选取同一岩性的岩体相关力学参数指标加以计算, 方便了岩体稳定评价中参数的选取, 对分析边坡稳定性以及后续开挖方案设计具有重要的参考意义。
