基于多尺度多方向Gabor滤波器的角点检测

景军锋，李 宁，章为川

(西安工程大学 电子信息学院，陕西 西安 710048)

0 引 言

角点作为图像重要的稀疏特征，在目标跟踪[1]、图像配准[2]、立体视觉技术[3]等领域有着广泛的应用。国内外学者就角点检测开展了大量的研究，根据角点判定依据的不同，可将现有的角点检测算法分为3类：基于边缘轮廓的角点检测算法[4-7]、基于模板匹配的角点检测算法[8-10]和基于灰度强度变化的角点检测算法[11-13]。基于边缘轮廓的角点检测算法首先利用边缘特征提取算法获取测试图像的边缘轮廓，再通过分析轮廓曲线的形状变化判定角点。基于模板匹配的角点检测算法将预先定义的角点特征模板与目标图像区域相匹配，借助二者的相似程度判定最终的角点。基于灰度强度变化的角点检测方法通过分析目标像素的强度变化信息，直接判定角点；该类方法以Harris检测器[11]与SIFT检测器[12]为代表，计算简便、角点特征鲁棒性较高，在实际应用中有着广泛研究。

二维Gabor滤波器由于良好的空间定位特性和方向选择特性[14]，在角点特征检测方面有着大量的研究。SHEN等研究发现二维Gabor滤波器在图像的局部特征提取上具备优势[15]；后续QUDDUS等将2个不同带宽的低通Gabor滤波器作差，迭代利用该差分模板进行角点检测，但该算法仅适用于结构较简单的小尺寸图像[16]。GAO等对测试图像进行Log-Gabor小波变换，结合小波变换系数构建了筛选角点的二维特征描述矩阵[17],但Gabor核函数的非正交性将加剧参数冗余[18]，降低了角点特征与其他像素的区分度。ZHANG等利用二维Gabor滤波器平滑边缘轮廓，建立已知轮廓像素的多尺度多方向角点判据[19],但对角点的筛选未涉及像素邻域的结构信息，检测结果的鲁棒性较差。综上所述，现有的基于二维Gabor滤波器的角点检测算法存在3个问题：一是未验证二维Gabor滤波器对各类角点的区分能力；二是仅采用目标像素在少数方向上的强度变化信息构建角点判据，易造成角点的漏检问题[13]；三是角点特征的描述仅统计目标像素的多尺度多方向信息，却忽略邻域像素的贡献，易造成角点的错检问题且稳定性较差。

针对上述问题，结合多方向结构张量积[13]提出了一种基于多尺度多方向Gabor滤波器的角点检测算法。首先，利用二维Gabor滤波器实部的方向导数描述各个角点模型(阶跃边缘、L型、Y型、T型、X型、星型)的强度变化特性，并提取各个角点模型表征的差异；再结合目标像素在各个方向上的强度变化信息建立相应尺度的多方向结构张量积，以解决因不合理的邻域信息统计而造成的角点漏检与错检问题；最后，利用多方向结构张量积的特征值构建新的角点测度，并结合多尺度筛选机制确定最终的角点。将本文算法与7个经典的角点检测器在图像仿射变换和噪声干扰条件下进行了一致性实验[20]，结果表明提出的算法拥有良好的检测鲁棒性，并且基于标定角点的匹配实验[7]也验证了新设计算法的定位精度。

1 二维Gabor滤波器

1.1 二维Gabor函数及其方向导数

在空域中，二维Gabor滤波器是一个正弦平面波与高斯核函数的乘积[21]，可表示为

exp(j2πfx′)

(1)

式中：x′=xcosθ+ysinθ,y′=-xsinθ+ycosθ;f为滤波器的中心频率；(γ,η)分别为沿着x轴与y轴2个方向上的锐度参数；θ为调制平面波和高斯主轴之间的夹角。

针对输入图像I(x,y)，利用二维Gabor滤波器实部φf,θ(x,y)进行平滑滤波，并提取图像I(x,y)在指定方向上的强度变化信息，有

(2)

式中：⊗为卷积操作；▽f,θI(x,y)为图像I(x,y)在指定方向θ(θ∈[0,2π))上的灰度变化。二维Gabor滤波器实部φf,θ(x,y)的方向导数可表示为

(3)

在实际应用中，输入图像往往为二维离散信号I(m,n)，因此图像在指定方向上的灰度变化表征也应该作离散化处理。给定中心频率参数f、锐度参数(γ,η)，则在指定方向θk上的导数离散化表示为

(4)

式中：m′=mcosθk+nsinθk,n′=-msinθk+ncosθk,θk=2kπ/K,k=0,1,…,K-1;K为统计的方向总数；θk为第k个方向；(m,n)为笛卡尔直角坐标系下的二维离散坐标。对于输入图像I(m,n)，强度变化信息在指定方向θk上的离散化可表示为

(5)

式中：mx与my为坐标偏移量。

1.2 区分基础角点模型

基础角点模型[13]如图1所示，共包含阶跃边缘、L型角点、Y型角点、T型角点、X型角点和星型角点6种模型，其他类型的角点均可由上述6种模型叠加生成。

(a) 阶跃边缘 (b) L型角点 (c) Y型角点

(d) T型角点 (e) X型角点 (f) 星型角点图 1 6种不同的角点模型Fig.1 The six different corner models

针对不同的角点模型，利用二维Gabor滤波器实部的方向导数描述模型O点处的局部灰度变化，各个角点模型的强度变化信息如图2所示。

(a) 边缘响应 (b) L型角点响应 (c) Y型角点响应

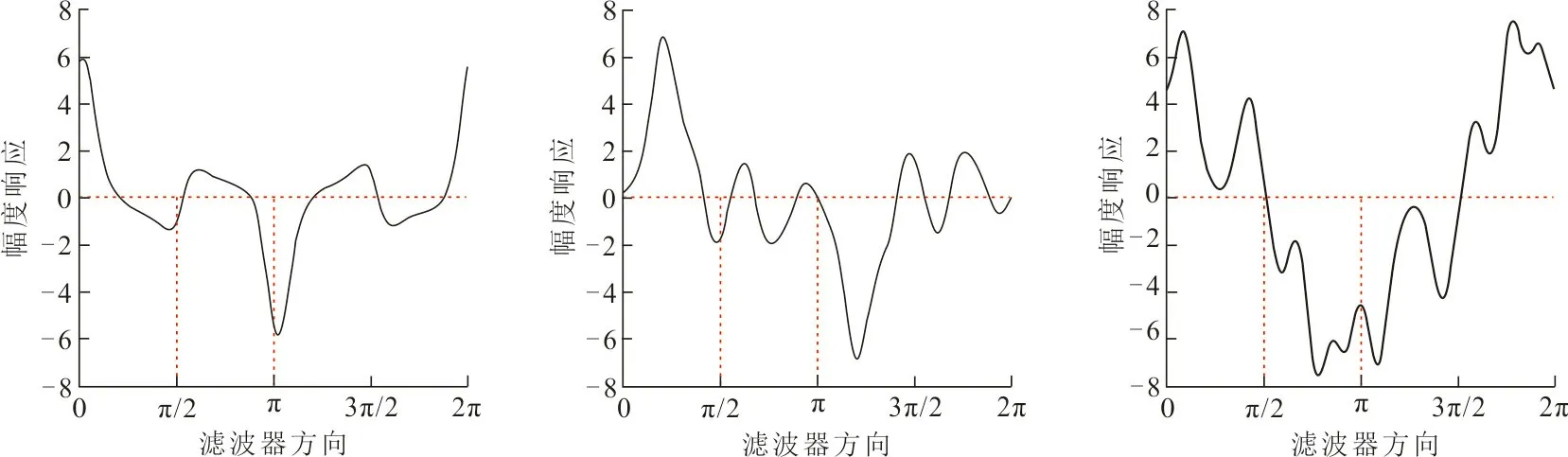
(d) T型角点响应 (e) X型角点响应 (f) 星型角点响应图 2 各个角点模型的强度变化信息Fig.2 The strength change information of each corner model

从图2可以看出，二维Gabor滤波器实部的方向导数能够对阶跃边缘和其他5种角点模型作显著的区分,并且能够显著地提取各个角点模型的差异。通过分析图2(b)、图2(d)和图2(e)发现，若仅统计水平与垂直2个方向上的灰度变化信息检测角点[11]，当相应的角点在水平或垂直方向上的强度变化偏弱时，易造成角点的错检与漏检问题。因此，本文将采用多方向策略，统计多个方向上的强度变化信息构建角点特征表征，以克服角点的漏检与错检问题，提取准确、强鲁棒性的角点特征。

2 一种新的角点检测算法

2.1 构建多方向特征描述矩阵

在二维笛卡尔坐标系下，利用二维Gabor滤波器实部的方向导数描述目标像素点在特定方向上的强度变化。先通过式(4)构建大小为(u+1)×(v+1)的滤波模板，再对目标像素(m,n)处的灰度变化进行刻画，即

[(▽f,1I(m+i,n+j),

▽f,2I(m+i,n+j),…,

▽f,K-1I(m+i,n+j),▽f,KI(m+i,n+j)]

(Δt,Δt,…,Δt)T]2=

(6)

式中： ▽f,KI(m+i,n+j)为像素点(m+i,n+j)在方向θK上的导数信息；Δt为坐标偏移量；Z(m,n)为各方向梯度差平方的加权和；M为结构张量积，即目标像素(m,n)处的K维特征描述矩阵。

2.2 建立角点判据

经典的Harris检测器[11]仅采用水平与垂直2个方向上的灰度变化信息建立二维特征描述矩阵，并利用特征描述矩阵的特征值筛选角点特征。由于该二维特征描述矩阵[11]无法提取到足够的特征描述信息，会存在角点的错检和漏检问题[21]。为更加准确地描述目标邻域的结构信息，通过式(6)提取目标像素在K个方向上的强度变化信息，并构建多方向结构张量积。对Harris检测器的角点判据进行拓展，利用多方向结构张量积的K′个特征值{λ1,λ2,…,λK′}构建新的角点测度，得

(7)

式中：v为极小的值，可避免发生分母为零的状况。

通过二维Gabor滤波器描述测试图像在各个方向上的灰度变化，构建相应的角点测度响应图；并结合非极大值抑制操作和多尺度筛选机制，筛选出强鲁棒性、定位准确的角点特征。新提出检测器的算法流程如图3所示。

图 3 新提出检测器的算法流程

具体的算法步骤如下：

第1步 通过式(4)与式(5)提取测试图像在各个方向上的强度变化信息。

第2步 结合目标像素在各个方向上的强度变化信息，构建目标邻域的多方向结构张量积M以描述目标局部的结构信息。

第3步 在每个像素点，通过式(7)生成相应的角点判据，构建对应尺度的角点测度响应图。

第4步 在小尺度的平滑条件下，对角点测度图中的各个像素进行初步筛选。在5×5的邻域范围内，若对应的角点测度不小于门限阈值Th且为局部极大值，则确定为候选角点；否则，删除。

第5步 对第4步中得到的各个候选角点，若对应的角点测度在各个尺度上均不小于门限阈值Th，则标记为最终角点。

3 结果与分析

为验证本文算法的角点检测性能，采用ANDD算法[7]、FAST算法[9]、Harris算法[11]、DOG算法[12]和FAGDD算法[13]、Harris-Laplace算法[22]、SURF算法[23]共7种经典的检测器与其进行性能比较。其中，本文算法的参数设置如下：尺度参数(f1=0.3,f2=0.2,f3=0.15);锐度参数(γ=0.5,η=0.9);门限阈值Th=1012；其他经典的检测器均采用默认最优值。实验平台将采用配置为i7-9750H、2.60 GHz与8 GB运存的操作系统和MATLAB(2016a)的实验仿真环境。

3.1 仿射变换与噪声干扰实验

借助仿射变换与噪声干扰实验[20]，对比本文算法与其他7种经典的检测器在图像旋转、JPEG图像压缩、一致性尺度变换、剪切变换、非一致性尺度变换和高斯噪声干扰条件下的角点效果一致性。将角点检测器在原始输入图像上将测到的角点数目记为Nori。测试图像经变换后，检测器提取到的角点数目记为Ntr，其中，重复检测到的角点位置数量记为Nsm。依据上述角点检测效果，利用平均重复率Ravg度量检测器在图像变换情况下的检测鲁棒性,可表示为

Ravg=(1/Nori+1/Ntr)×Nam/2

(8)

实验将采用如图4所示的灰度测试图集进行一致性分析实验[20]，该测试集共包含24张不同尺寸大小的灰度图像，在图像仿射变换与高斯噪声干扰条件下将生成4 992个测试场景。8种算法检测器的一致性分析结果如图5所示，检测器在图像变换下的平均重复率如表1所示。

图 4 一致性实验测试图像集Fig.4 Test image set for consistency analysis experiment

(a) PEG图像压缩 (b) 旋转变换 (c) 高斯噪声干扰

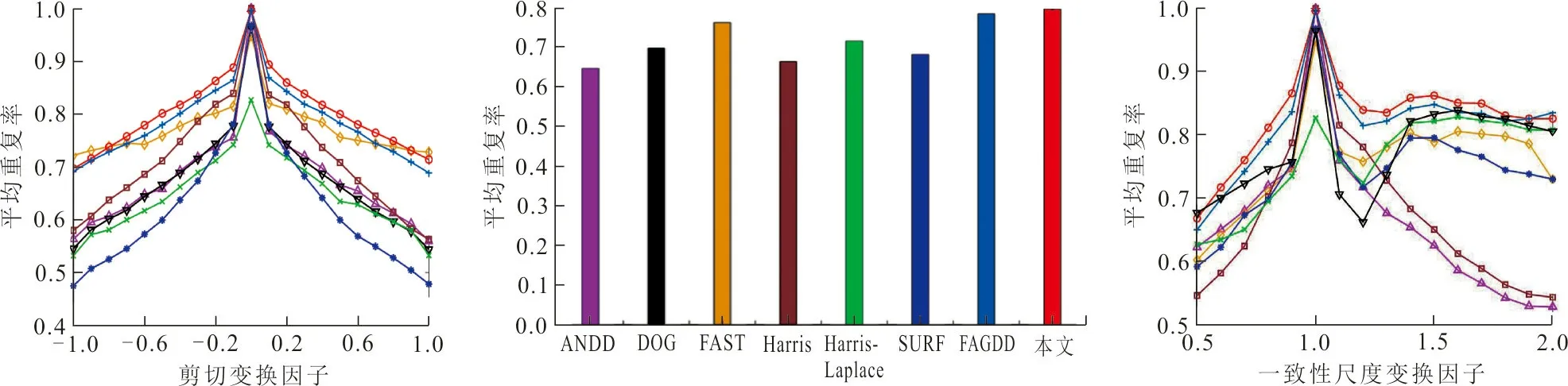
(d) 剪切变换 (e) 不同算法的非一致性尺度变换 (f) 一致性尺度变换

表 1 检测器在图像变换下的平均重复率Tab.1 The average repeatability of detectors under image transformation

从图5可以看出，本文算法在JPEG图像压缩、高斯噪声干扰、剪切变换和2种尺度变换条件下，检测鲁棒性均优于其他7种角点检测算法。其中，在面对旋转变换、剪切变换和尺度变换时，由于二维Gabor滤波器具备良好的空间定位特性和方向选择特性，本文算法相较于其他检测器表现出更佳的检测鲁棒性,并且二维Gabor滤波器实部具备良好的滤波降噪效果，因此本文算法在面对高斯噪声干扰时，检测效果远超其他算法。

从表1可以看出，各个检测器在面对各类图像变换时的重复率比较结果发现，FAGDD算法和本文算法表现最佳。2种检测器均利用多方向结构张量积统计目标像素在局部邻域中各个方向上的强度变化信息，有效避免了因统计方向较少而导致的错检与漏检问题，并有效提取了目标邻域的局部结构信息，有助于真实角点特征的筛选与定位，使检测器表现出更佳的检测鲁棒性。

3.2 基于标定角点的匹配实验

(9)

将Harris算法、FAST算法、FAGDD算法与本文算法在图6的2幅测试图像上进行角点检测，并比较相应的定位精度，图6(a)包含59个真实角点，图6(b)包含84个真实角点。Harris算法、FAST算法、FAGDD算法和本文算法对图6(a)进行角点检测，错检率分别为0.164、0.333、0.089和0.000，漏检率分别为0.230、0.253、0.305和0.220，定位误差分别为2.038、1.568、1.906和1.474；Harris算法、FAST算法、FAGDD算法和本文算法对图6(b)进行角点检测，错检率分别为0.718、0.578、0.017和0.000，漏检率分别为0.452、0.243、0.321和0.214，定位误差分别为1.216、1.201、0.889和1.037。

(a) 积木图像

(b) 几何图像图 6 测试图像的标定角点图Fig.6 Calibration corner map of test image

通过比较发现，本文算法在错检角点、漏检角点和定位误差3个方面均优于其他算法。在定位误差方面，由于FAGDD算法与新提出的检测器均采用多方向结构张量积表征局部强度变化，描述目标像素的局部结构信息，有助于提升角点的定位精度；并且采用多尺度筛选也可进一步剔除检测结果中鲁棒性较差的像素点，减少错误的角点数量。

4 结 语

本文充分考虑二维Gabor滤波器良好的空间定位特性与方向选择特性，利用二维Gabor滤波器实部的方向导数提取输入图像在各个方向上的灰度变化信息，构建了多方向结构张量积，并结合多尺度筛选机制，提出了一种检测鲁棒性好、定位准确性高的角点检测器。同时，利用二维Gabor滤波器实部的方向导数描述各个角点模型的强度变化差异，能有效区分阶跃边缘和各类角点模型；并利用多方向结构张量积描述目标像素邻域在各个方向上的灰度变化信息，充分考虑了邻域像素的贡献，有效解决了角点的漏检和错检问题，且增加了角点特征的鲁棒性。在未来的工作中，将为该检测算法匹配合适的特征描述方式，以适应更多的视觉应用场景。