基于图像四叉树网格的结构动力响应分析
2021-07-12杜成斌李欣竹田新冉黄文仓
杜成斌 李欣竹 田新冉 黄文仓
(河海大学 力学与材料学院,南京 211100)
在数值计算中,网格划分的质量是影响计算精度和计算效率的重要因素.常规有限元网格划分无论是利用软件还是人工剖分,网格均不允许存在悬挂节点,因此在材料分区和复杂边界附近均需用较密的网格进行过渡,既增加网格生成的工作量,也降低了结构计算效率.
Matlab软件有强大的计算性能,其内置函数imread可以从图像文件中读取灰度或彩色图像,进而利用内置函数qtdecomp对图像进行四叉树分解,因此可以快速划分网格,但是直接与有限元(finite element method,FEM)结合会产生悬挂节点[1].将其与新近提出的比例边界有限元法(scaled finite element method,SBFEM)结合可克服有限元法对网格剖分不允许存在悬挂节点的问题[2].比例边界有限元法是由Song和Wolf[3-5]提出的一种新型半解析数值计算方法,其应力场和位移场在径向是解析的,环向具有与有限元相同的精度,且仅需对结构的边界进行离散,降低了一维计算维度.自提出之后,SBFEM得到快速发展.
Birk等[6]首次提出基于图像四叉树网格与SBFEM相结合的方法并模拟了地震波在不均匀土壤中的传播;Ooi等[7]提出了基于混合多边形和四叉树网格相结合的SBFEM算法,高效地模拟了裂纹扩展问题,且网格对复杂的边界有更好的适应性;随后Albert Saputra等[8]基于图像的四叉树网格和八叉树网格进行了混凝土试件的静力分析,研究中SBFEM的单元为规则的正方形或正六面体,取得了比较好的效果.邹德高等[9]结合多边形比例边界有限元法和四叉树网格对面板坝进行跨尺度精细化静动力分析,计算结果与FEM计算结果非常接近.He等[10]将图像四叉树与SBFEM结合扩展到了非均质材料的导电性分析,并验证了该方法的合理性.以上研究中大多采用规则四叉树对结构进行剖分,研究对象大都为规则结构,如应用在不规则结构边界,会产生锯齿形状,与实际几何边界不符.
基于图像进行四叉树网格划分与SBFEM结合可克服FEM对网格剖分不允许存在悬挂节点的问题.一方面充分利用Matlab先进高效的图像读取功能,通过不同的像素对结构的材料进行自动分区,同时四叉树算法非常方便快捷,这些优势克服了传统的网格生成方法的缺陷,极大地提高了网格生成效率,使大家从繁琐的网格剖分中解脱出来,更适合非均质材料和复杂边界的网格过渡.另一方面利用比例边界有限元法半解析特点,可高效地进行结构动力分析以得到较高的计算精度.
本文采用一种基于图像与四叉树网格划分相结合的方式以实现结构的快速网格划分,在边界附近依实际几何边界对单元进行切割,以满足结构的实际几何边界条件,改进了以往大多单元模式仅为规则正方形、剖分后边界为锯齿形的缺陷.将其与比例边界有限元法相结合,建立基于图像的结构动力计算,极大减轻了以往计算网格生成过程的繁琐工作量,并通过两个算例验证了本文方法的先进性和高效性.
1 基于图像进行四叉树网格划分
1.1 四叉树数据结构
四叉树是一种树状数据结构,每个节点最多有四个子树.从四叉树的根单元开始逐层划分,每一个单元可以进一步划分为四个子单元,直到所有单元满足划分要求则停止.
四叉树可以快速实现网格划分,从1 m级到1 mm级仅需10层划分(210=1 024),且划分网格以正方形为主,可自动进行高质量单元的离散.
1.2 基于图像的四叉树网格划分步骤
1.2.1 图像导入以及最大、最小单元尺寸和阈值的确定
可以使用Matlab内置函数imread快速读取灰度图像并储存为N×N的数字矩阵,要求图像的像素值N必须为2的整数幂,才可以进一步进行四叉树划分.分辨率(Resolution)为结构实际尺寸除以N,其物理意义为一个像素代表的实际尺寸大小.矩阵中数字的大小代表颜色深浅,取值范围为0~255,0代表黑色,255代表白色,数值越大颜色越浅,因此可以用不同的颜色代表不同的材料.
Matlab内置函数qtdecomp可以对图像进行四叉树划分,在划分前需要确定最大、最小单元尺寸(MaxDim、MinDim)和阈值(QTthreshold).尤其在进行时域分析时应保证每个波长至少有10个节点才能识别波的传播[11],即一个波长内至少包含9个两节点线单元,由此确定最大单元尺寸.最大单元尺寸和最小单元尺寸必须是2的整数幂.网格大小要求最小的单元尺寸不能小于MinDim,最大的单元尺寸不能大于MaxDim,且要求相邻两个像素颜色强度的差小于QTthreshold,满足则停止划分网格,反之继续划分.
读取一个8×8像素大小的灰度图如图1(a)所示,该图像储存为对应的二维数字矩阵,如图1(b)所示.

图1 灰度图像及对应的图像矩阵
1.2.2 平衡四叉树网格剖分
对图1结构进行四叉树划分,设置MaxDim=4、MinDim=1、QTthreshold=2,遵循2∶1的原则进行四叉树划分,即相邻单元尺寸满足2∶1的平衡原则.
首先,将整个图形区域划分成4个大小相等的正方形单元,如图2(a).检查颜色强度的均匀性(即是否满足阈值条件);其次,进一步划分已经划分过的子域,如图2(b).第3次划分后满足所有条件,则停止划分,如图2(c).

图2 四叉树划分过程
经过平衡四叉树网格划分可能产生的单元类型共有6种,如图3所示,经4次旋转可得到全部24种单元类型,悬挂节点可以视为边界上增加一个两节点线单元,处理起来非常方便,因此SBFEM可允许存在悬挂节点,每个多边形都可以作为SBFEM中的一个计算子域.
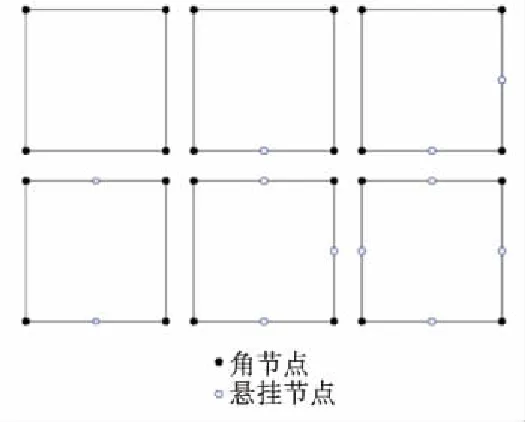
图3 遵循2∶1划分规则可能生成的多边形单元
1.2.3 边界单元的切割
为了适应结构实际几何边界条件,在边界处需要进行切割,可以将正方形单元依边界条件切割成任意多边形单元,具体形式如图4所示.
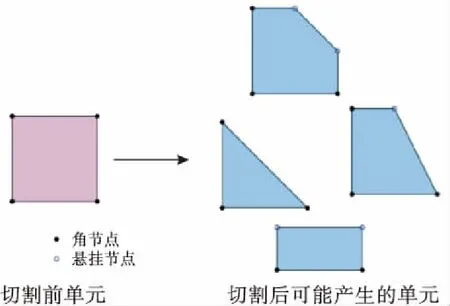
图4 经过切割可能产生的单元类型
2 比例边界有限元法基本理论
比例边界有限元法与有限元法类似,首先需要将整个结构的计算区域离散为一个或多个子域,然后再将所有子域的质量矩阵、刚度矩阵按顺序组合起来,最后由平衡方程求解出位移,根据几何方程和物理方程求得应变和应力结果.在每个子域内必须设置一个比例中心,比例中心的选取需要满足对整个子域边界可见的条件[12],以图5这个子域为例,将比例中心O放置在中心处,以O为原点建立局部比例边界坐标系(ξ,η),ξ为径向坐标,η为环向坐标沿着比例中心逆时针放置.对于子域内任意一点,笛卡尔坐标(x,y)可以用局部比例边界坐标(ξ,η)与形函数N(η)表示为

图5 子域模型
x=ξxb(η)=ξN(η)xb
(1)
y=ξyb(η)=ξN(η)yb
(2)
式中:xb=[x1,x2]T,yb=[y1,y2]T为子域边界上两节点线单元的节点坐标;N(η)=[N1(η),N2(η)]为两节点线单元的插值形函数.
由弹性动力学的基本方程可以推导得到SBFEM位移控制方程[13]:
E2u(ξ)+ω2M0ξ2u(ξ)=0
(3)
其中:u(ξ)为位移向量;ω为频率;E0、E1、E2、M0为系数矩阵,具体见文献[13].由方程(3)可得到单元的位移径向解析解.
单元的环向采用类似有限元的方法离散,引进插值函数,最终可建立整体运动方程:
(4)
3 算例分析
3.1 双材料板动力算例
如图6(a)所示,边长为L=400 m的正方形双材料板,材料参数分别为:E1=10 GPa,ν1=0.15,ρ1=2 800 kg/m3;E2=20 GPa,ν2=0.2,ρ2=2 600 kg/m3.边界条件为:y=0处为固定端,在y=400 m处施加y方向相反方向的冲击荷载,荷载随时间变化如图6(b)所示,最大值为400 kN.
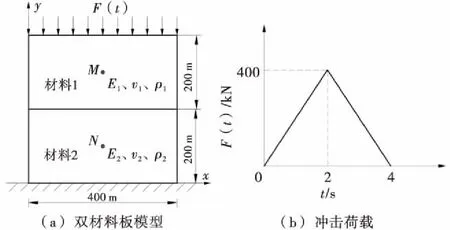
图6 双材料板模型及其所受冲击荷载
考虑该问题为平面应力问题,读取双材料板的模型的图像,像素值为512×512,材料1的颜色用98表示,材料2的颜色用198表示,如图7(a)所示,基于该图像进行四叉树网格划分.一个像素的大小代表0.78 m,即Resolution=0.78 m,选取MaxDim=64,MinDim=16,对应的真实尺寸分别为49.92 m,12.48 m,进行动力分析时,两种材料的网格疏密可以不相同,只需要在交界处加密,计算网格如图7(b)所示,共279个节点,232个单元.ABAQUS有限元计算网格如图7(c)所示,共289个节点,256个单元.采用Newmark时间积分求解动力方程,Newmark参数选择β=0.25,γ=0.5.
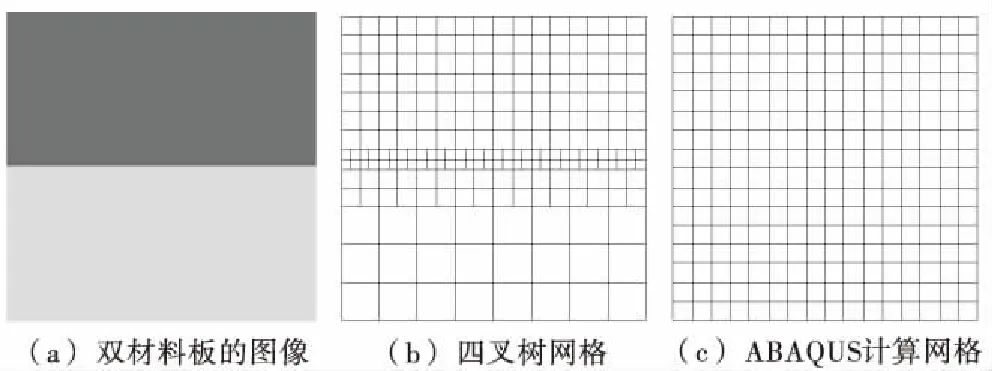
图7 双材料板的图像及其计算网格
基于上述方法对双材料板进行四叉树网格划分并采用SBFEM进行时域分析,计算总时间为20 s,增量步长为0.02 s.选取坐标为(200,300)的M点和(200,100)的N点,分别计算两个点的y方向位移和y方向应力,与有限元软件ABAQUS计算结果进行对比,如图8所示.
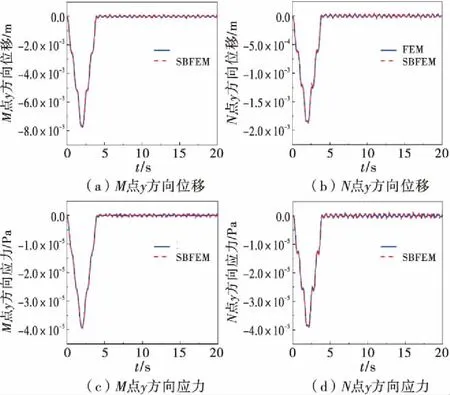
图8 M点、N点y方向位移及应力结果
对于双材料板的动力分析,为得到较高精度的结果,ABAQUS需要较密的计算网格,本文方法只需在两种材料交界处进行加密,可以实现粗细网格的过渡.本算例SBFEM仅需9.3 s,而ABAQUS需37 s,后者为前者的近4倍.结果显示,两种方法计算所得位移和应力结果非常接近,验证了该程序求解动力问题的正确性.
3.2 重力坝地震响应分析
某混凝土重力坝剖面示意图如图9所示.坝高为110 m,坝顶宽15 m,坝底宽75 m,假定坝上游为直立坡.采用无质量地基,地基范围分别由坝底向下和上游、下游两侧延伸至两倍坝高.坝体混凝土泊松比ν1=0.15,密度ρ1=2 643 kg/m3,弹性模量E1=31.027 GPa,假定采用Rayleigh阻尼反映混凝土的阻尼性质,即C=a0M+a1K,每一阶振型的阻尼比均取0.05,通过计算前两阶振型及自振频率,求出系数a0=1.010 21,a1=0.002 08.坝基材料泊松比ν2=0.3,弹性模量E2=20 GPa,将坝基与坝体看作一个整体,计算坐标系为:顺河向为x,竖向为y,建立比例边界有限元计算模型.计算中考虑坝体自重和地震荷载,重力加速度取g=9.81 m/s2,将地震力以惯性力的形式施加在坝体上.
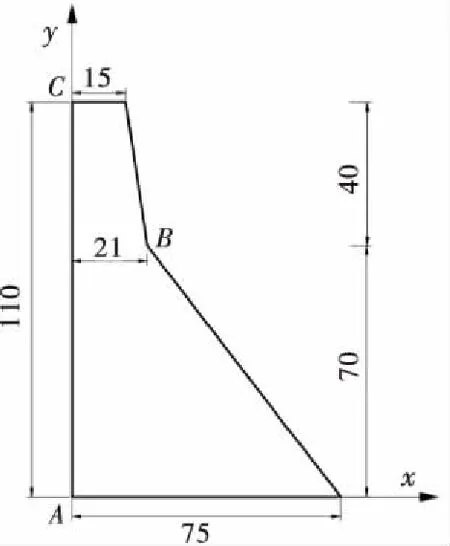
图9 混凝土重力坝剖面示意图(单位:m)
输入的地震波E1 Centro水平向加速度时程曲线如图10所示,竖直方向地震波取水平向的2/3,地震作用总时长为30 s,计算时间增量步长选取为0.02 s,边界条件为:坝基两侧水平方向位移固定,坝基底部固定边界.采用Newmark法进行动力计算,Newmark参数选择β=0.25,γ=0.5.
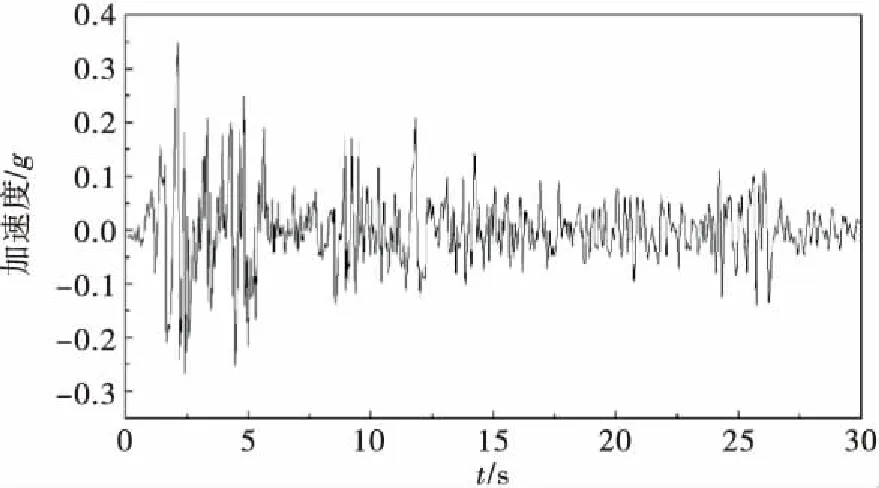
图10 水平向E1 Centro地震时程曲线
将重力坝具体尺寸的图形导入程序中,生成像素值为1 024×1 024的灰度图像如图11(a)所示,如果有材料分区,只要不同的材料分区用不同颜色表示即可.一个像素的大小代表0.5 m,即Resolution=0.5 m,选取MaxDim=128,MinDim=1,对应的真实尺寸分别为64 m,0.5 m,基于该图像进行四叉树网格划分如图11(b)所示,为了更好地模拟重力坝的边界,采用前述单元切割法对边界处的四叉树单元进行切割形成任意多边形单元.图11(c)为ABAQUS有限元网格图.
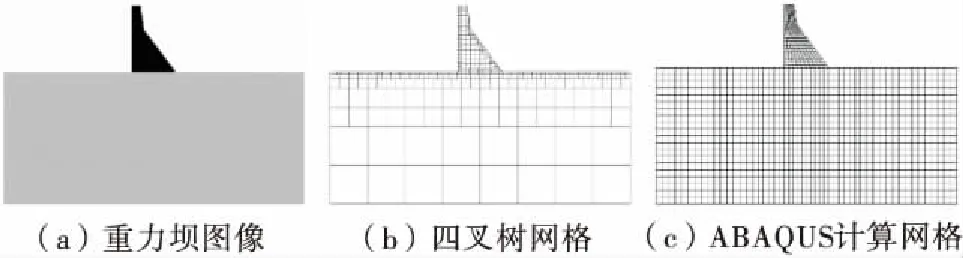
图11 重力坝图像及其计算网格
选取坝踵、下游坝面折坡面处、坝顶上游处(如图9所示A、B、C)3个点作为关键点进行时程观测,输出A、B、C3点的x方向位移时程曲线和A、B两个点的x方向应力时程曲线,并与有限元软件ABAQUS计算所得结果进行对比,3点的水平向位移时程曲线如图12所示,A、B点的x方向应力时程曲线如图13所示.
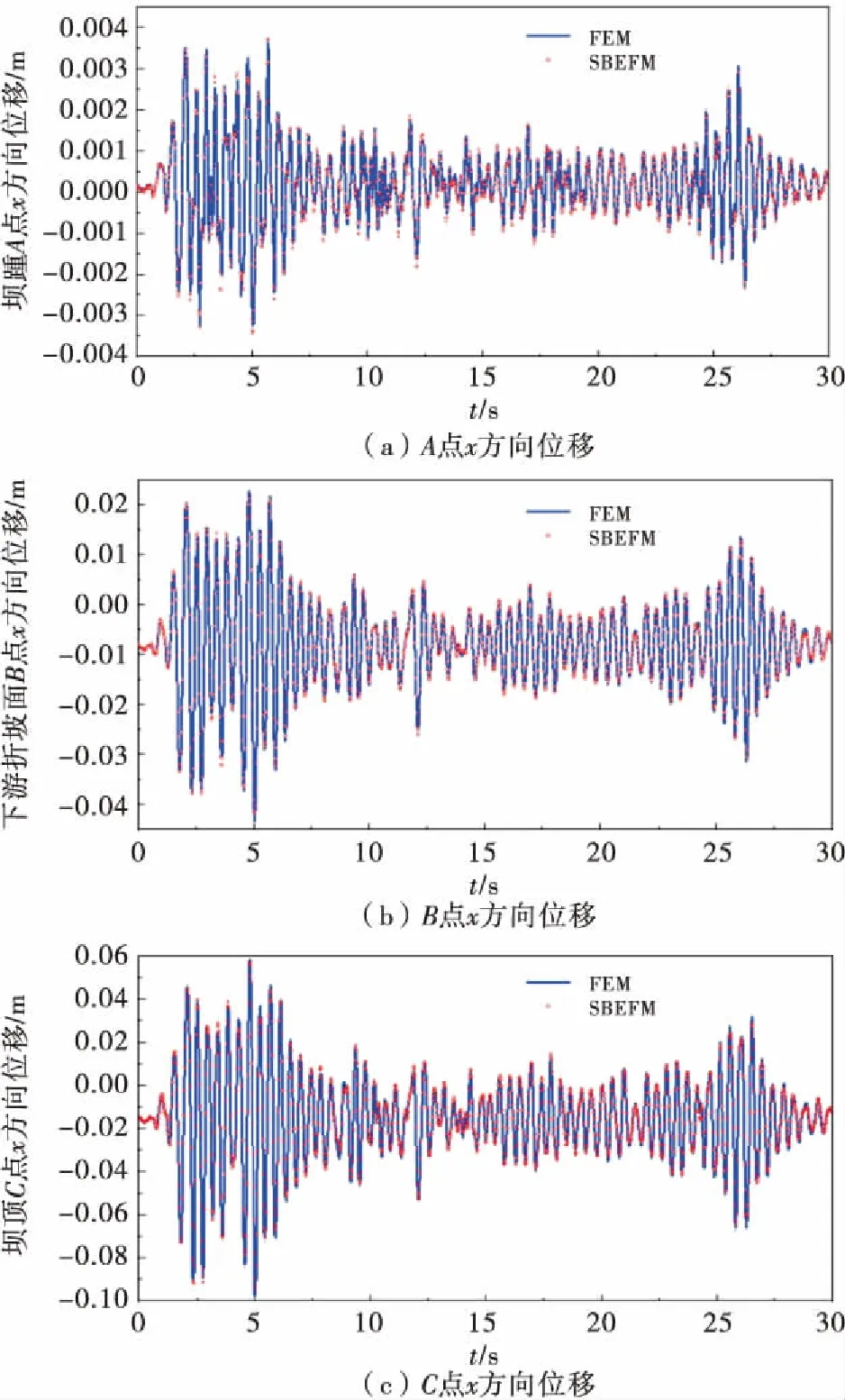
图12 A、B、C点x方向位移时程曲线
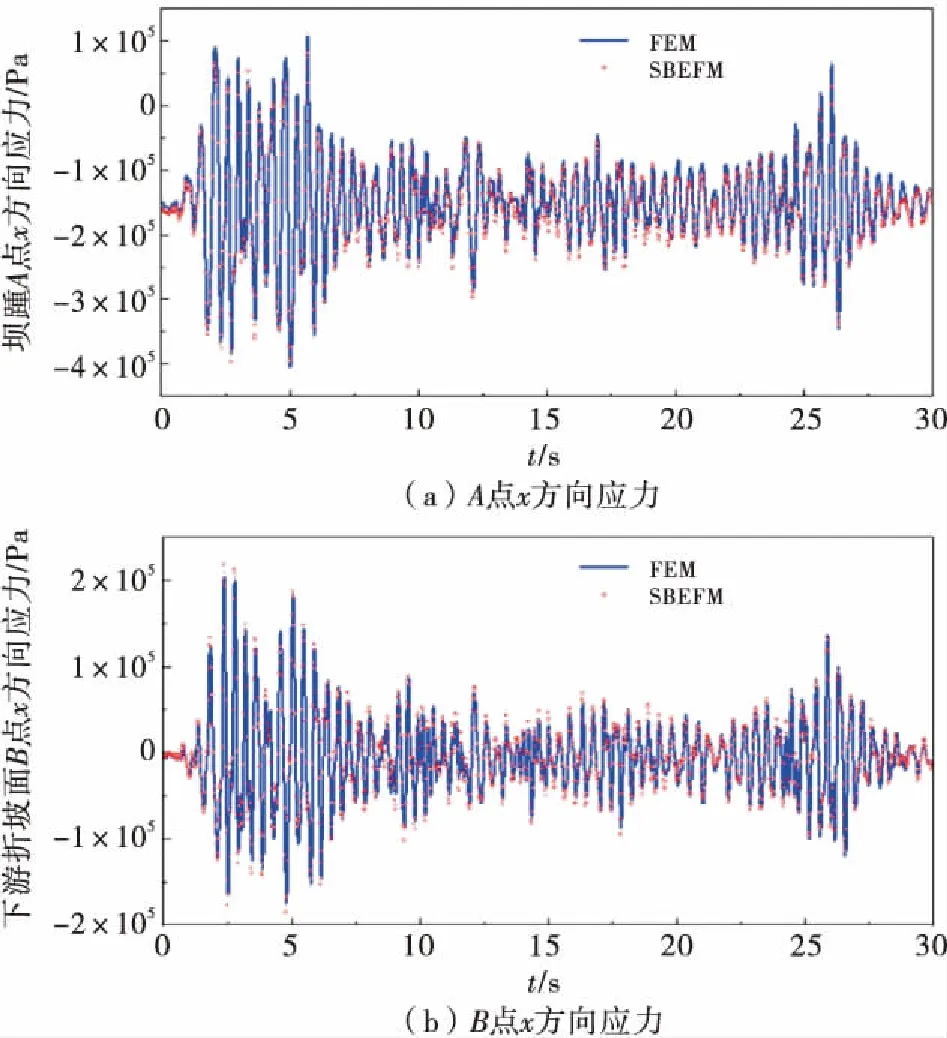
图13 A、B点x方向应力时程曲线
其中ABAQUS有限元的节点总数1 377,单元总数1 234,自由度数为2 754;SBFEM节点总数627,单元总数445,自由度数为1 254,这些数值均只有有限元的36%~46%.从计算时间来看,SBFEM只需201.1 s,而ABAQUS需462 s,后者是前者的2.3倍.由图12、13可知,本文方法计算所得结果与ABAQUS计算所得结果非常接近,但相比有限元节省了大量的计算自由度.
4 结 论
基于图像进行四叉树网格划分,能够实现网格的快速划分以及不同材料之间网格的粗细过渡,与比例边界有限元法相结合,避免了有限元模型中的悬挂结点问题.本文将边界切割引进四叉树生成的正方形单元,可以依边界条件将正方形单元切割成任意多边形单元,避免以往四叉树单元生成的边界为锯齿形的缺陷.数值算例表明,与有限元模型相比,本文方法极大减小了结构网格生成的前处理工作量,且粗细网格过渡方便快捷,模型的单元数、结点数目均大大减少,不仅有较高的计算精度,而且也有较高的计算效率,是一种非常有前景的新型结构计算方法.
