追根溯源 打通联系 构建网络
2021-07-11陈瑛
陈瑛
【摘 要】总复习课,既要“温故”,更要“知新”,贵在“生长”。笔者尝试打破复习课“梳理知识结构+练习巩固”的固有格局,将练习融入知识梳理中,引导学生追根溯源、打通联系、构建网络,让知识更具结构化,更有生长性。
【关键词】小学数学 立体图形 总复习
一、画图表征,追根溯源
1.导图梳理引思考
课前,学生对立体图形的表面积和体积的知识进行了自主梳理,将其画成了思维导图,并把相关知识融入、浓缩到图中,甚至还有学生查阅资料,拓展了圆锥表面积的计算公式,并且对圆柱表面积的新算法进行了补充。遗憾的是,极少有学生尝试去打通这些已有知识之间的联系,更难看到知识的产生和推导过程。
从学生的思维导图中可以看出,学生对表面积和体积的认识还停留在一个个零散的点状知识上,并未对知识的本质进行勾连,也极少有知识的生长。很少有学生关注体积是如何推导出来的,要打通立体图形之间的联系,体积的本质属性一定要通透。
2.画图表征凸本质
为此,笔者将课前梳理设计成画示意图说明如何求给定数据的立体图形的体积,学生在课前进行回顾与梳理,画出体积推导过程,用图进行表征。图画出来了,学生对体积的理解就更深刻了。
在这个教学环节中,笔者看到了学生活学活用的样态,通过回忆、整理、交流,从不同角度阐释了这些立体图形之间的内在联系,直观形象地呈现了体积公式的推导过程。如此,“透视”了知识的核心,从知识本质处深入,不仅回顾旧知,还通过内化和还原,促进学生对知识的理解,实现认知结构的优化,感悟了数学思想。
二、打通联系,构建网络
立体图形表面积和体积的学习分散在六年级上、下两册的教学上,学生较少关注知识间的关联。但长方体、正方体和圆柱都是直柱体,知识之间存在着一致性。六年级下册的总复习课,若要打通知识间的联系,关键在“统”。
1.一统体积:凸显本质
总复习课,要打通知识间的联系,构建完整的知识体系。学生通过梳理,打通长方体、正方体和圆柱体积之间的内在联系,实现统一的体积计算,学生的点状知识已在潜移默化中串成了线,并逐渐形成知识网。
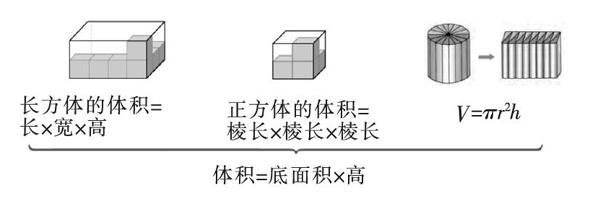
长方体和正方体的体积都是求有多少个这样的体积单位,可以先算一层,再乘层数,即底面积乘高。圆柱通过转化变成近似的长方体,也可以理解为求多少个这样的体积单位,同样可以用底面积乘高来计算。这个过程实现了体积计算的统一,这个统一的过程是建立在学生已有的认知基础之上,并衍生新的认识,将三个体积计算公式化归成一个,甚至从这一个公式可以继续生长成多个立体图形的体积计算公式。
2.二统侧面:实践拓展
笔者用一张A4纸,用同样的彩纸,做出无底面的长方体和圆柱,打通侧面积、表面积之间的联系,同时进行拓展延伸,为第三学段的学习埋下知识生长的种子。
小组合作,用彩纸做圆柱和长方体。要求:不改变纸的大小,不能有重叠,做出尽可能多的不同形状的圆柱和长方体。
师:先来说说圆柱吧。
生1(边说边做):卷一下就可以了。
师:两种不同的方式,卷出了没有底面的圆柱,它们有什么相同的地方吗?
生2:侧面积一样,都是这张长方形纸的面积。
师:你是怎么做长方体的?在做的时候要注意什么?
生3:可以将一条边对折再对折,平均分成4份,折出长方体。
师:这种方式折出来的长方体有什么共同点?
生3:侧面积一样。有两个面都是正方形,其余四个面完全相同。
师:有没有不是平均分,但是也做成长方体的?
生4:只要两条长一样,两条宽一样,就可以折成长方体。
师:这些长方体大小、形状不一样,有没有相同的地方?
生5:侧面积相同,因为是同一张纸折成的。
师:刚才我们用同样的彩纸,做出了不同的长方体和圆柱,它们之间有联系吗?(侧面积相同)它们的侧面展开又分别是什么?长方形的长是这个立体图形的?(底面周长)宽呢?(高)
(教具演示)换种做法,一条边是这个立体图形的底面周长,另一条边就是它的高。
(讨论得出:侧面积=底面周长×高)
整个活动过程,不仅对小学阶段的立体图形进行了梳理,同时进行了拓展和延伸,为第三学段进行铺垫,让知识有生长点。学生通过一张A4纸,在卷一卷、折一折等活动中,逐渐理解长方体和圆柱的侧面积与这张A4纸之间的联系,发现其中蕴藏的奥秘,统一侧面积的计算方法。在此过程中,主动建构结构化、可迁移的认知系统,学生在做中学、做中悟、做中思,培养了类比推理的能力。
3.三統表面:完善体系
学生经历两次“统”的过程,已有了“统”的意识和经验,因此,对于第三次“统”,笔者放手让学生大胆猜测,发掘经验,尝试独立发现和归纳,产生新的结构,充分突显主体性。
师:既然长方体、正方体、圆柱的体积和侧面积我们都找到统一的公式来计算,它们的表面积也能用同一个公式表达吗?你认为是什么?
(表面积=侧面积+底面积×2)
师:在解决表面积的实际问题时,一定是用一个侧面积加两个底面积吗?
(1)一侧无底
(呈现学生作品)现在这个圆柱、长方体的表面积指的是什么?(侧面积)生活中有这样的情况吗?
生(举例):通风管,压路机压路的面积……
(2)一侧一底
如果给这个圆柱或长方体或正方体配一个底面,它的表面积是指什么?
这是我们解决过的哪类问题?(无盖水桶、游泳池、鱼缸等)
(3)一侧两底
配两个底面呢,现在表面积又是什么?
立体图形的表面积在生活中并不一定都是用一个侧面积+两个底面积,这一环节,看似无意却有意,看似无题却多题。学生经历了观察、想象、举例、迁移等过程,在以后的解题中,会有意识地从题目本身出发,发掘本质,准确辨别这是哪一类问题。
4.创作图形:拓展延伸
师:用这张彩纸,你还能做出其他立体图形吗?
(生独立创作,全班交流)
师:仔细观察这些立体图形,有什么特点?(引出直柱体)
师:你认为直柱体还可以长成什么样子? 这些直柱体在计算侧面积、表面积和体积时,有统一的方法吗?
生1:因为都是同一张纸做的,它们的侧面积相同。
生2:表面积都是一个侧面积+两个底面积。
生3:体积是底面积乘高。
师:体积是否一定这样计算?老师给同学们打个问号,任何结论都需要大胆猜想,小心求证,直柱体的体积计算留给爱思考的同学课后去推导求证,相信你一定会有所发现。
一张A4彩纸,学生通过动手操作,可以变成认识的或者是不认识的立体图形,可以解决现在能解决的问题,甚至是未来能解决的问题。既有基础图形的操作,又打开了学生的脑洞,还可以折更多的直柱体。立体图形体积、表面积、侧面积的计算公式分别从多个统一成了一个,又从一向多进行了拓展,这样的学习对学生来说是有生长性的,这是新的认知结构构建的过程。
三、精选练习,深度理解
练习巩固是形成知识结构和发展学生能力的重要环节。本课侧重于知识的梳理和打通,练习的设计贯穿于活动中,并进行了整合和提炼,既有保底的巩固,又有思维的拓展,体现知识间的勾连,帮助学生深度理解与应用,提升数学素养。
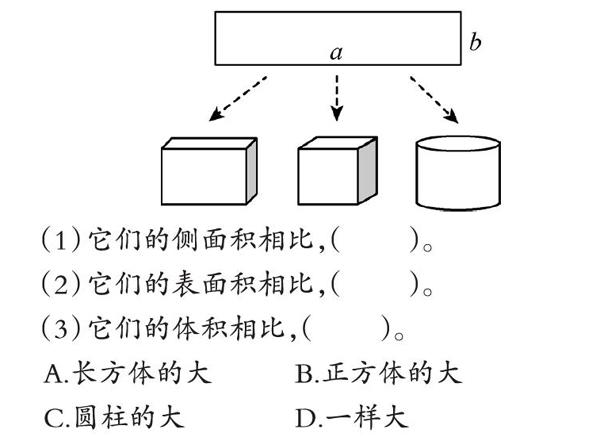
练习1:如图,以长方形纸的边a作底面周长,边b作高,分别可以围成一个长方体、正方体和圆柱体纸筒,再分别给它们另作一个底面。
(1)它们的侧面积相比,( )。
(2)它们的表面积相比,( )。
(3)它们的体积相比,( )。
A.长方体的大 B.正方体的大
C.圆柱的大 D.一样大
这题放在了“三‘统”之后,学生对立体图形表面积和体积之间的联系有了深入理解后,用此题来帮助回顾与拓展,更有利于知识的内化。侧面积的比较,学生脱口而出是相同的,因为用了同一张纸,侧面积就是这张长方形纸的面积,这是学生刚刚经历后所内化的结果。要比较表面积的大小,重点在于底面积,此时与三年级学习的周长和面积建立了联系,底面周长(长方形的长)相同时,围成的圆的面积更大,因此圆柱的表面积大。体积有了前面比较的经验,就更容易得出结论了。
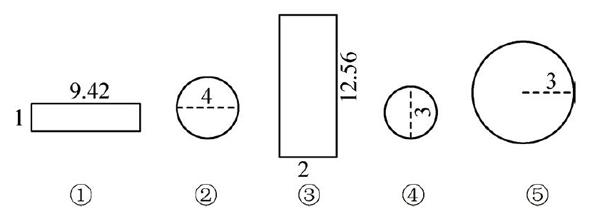
练习2:请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。(单位:分米)
(1)你选择的材料是( )号和( )号。
(2)用你选择的材料制作的水桶,表面积和容积各是多少?
此题既开放又综合,不仅要关注图形特征,还需关注数据特征,通过计算来实现合理选择和搭配。如果选择①为侧面,9.42作为底面周长的话,底面直径为3,即图④,此时1就是圆柱的高;如果選择③为侧面,12.56是底面周长,底面直径为4,即图②,高为2。通过选择和分析,得出必要的数据,从而计算无盖圆柱的表面积和容积。
布鲁纳认为,学习的过程实际上是利用已有的认知结构,对新的知识经验进行加工改造并形成新的认知结构的过程。笔者认为,总复习课既要打通知识间的联系,更要更新已有的知识体系和认识结构,让知识具有生长活力和生命张力,发挥“磁力场”,呈现灵动舒展的课堂样态,实现对数学知识结构的表征与内化,将数学知识由“厚”变“薄”,由“薄”变“厚”,努力实现从“教学生一课”到“教学生一生”的转变,构建清晰网络,深化数学素养。
【参考文献】
刘贤虎,阳海林.打通总复习教学的“任督二脉”[J].教学与管理,2017(2).
