钢桥面板疲劳裂纹损伤非线性Lamb波检测的数值模拟与试验研究
2021-07-11申伟郑芳彤李冬生
申伟 郑芳彤 李冬生
摘 要:为有效识别车辆荷载作用下钢桥面板的早期疲劳裂纹,进行钢板疲劳裂纹非线性Lamb波检测的数值模拟和试验研究。基于声接触非线性理论,提出了首波能量、拟声速和非线性参数3个损伤指标。试件同时考虑了孔洞缺陷、宏观裂纹和疲劳裂纹3种类型的缺陷,其中,疲劳扩展裂纹通过疲劳加载试验生成。在三维数值模型中,通过零长度非线性弹簧单元模拟闭合裂纹的“呼吸效应”,以模拟Lamb波与疲劳裂纹的局部非线性相互作用过程;进行了非线性Lamb波步进式扫描,并通过带通滤波器提取了二次谐波响应。研究结果表明:基波能量和拟声速指标对宏观缺陷敏感,而二次谐波能量和非线性参数对疲劳裂纹更敏感,综合3个损伤指标可以同时实现宏观缺陷和疲劳裂纹的识别和定位。
关键词:钢桥面板;疲劳裂纹;非线性Lamb波;非线性参数
中图分类号:U448.36 文献标志码:A 文章编号:2096-6717(2021)03-0135-07
Abstract: In order to effectively identify the early fatigue cracks of the steel bridge deck under vehicle loads, the numerical and experimental research on the nonlinear Lamb wave detection of steel plate fatigue cracks were carried out. Based on the non-linear theory of acoustic contact, three damage indexes were proposed, which are first wave energy, pseudo sound velocity and nonlinear parameter. Three types of defects including hole defect, macro crack and fatigue crack were considered in the specimens. Among them, the fatigue growth crack was generated by the fatigue loading test. In the three-dimensional numerical model, the "breathing effect" of closed crack is simulated by a zero-length nonlinear spring element to simulate the local nonlinear interaction process between Lamb waves and fatigue cracks. In the experiment, the nonlinear Lamb wave stepped scanning was performed, and the harmonic response was extracted through a band pass filter. The research results show that the first wave energy and pseudo sound velocity are sensitive to macro defects, while the harmonic waves energy and nonlinear parameter are sensitive to fatigue cracks. Combining the three damage indexes can simultaneously achieve the identification and location of macro defects and fatigue cracks.
Keywords: steel bridge deck; fatigue crack; nonlinear Lamb waves; nonlinear parameter
鋼桥面板在服役期间长期承受车辆荷载引起的交变应力作用,极易产生疲劳裂纹。金属的疲劳寿命一般分为3个阶段:即材料特性退化阶段、微裂纹的形成与积累阶段和疲劳断裂阶段[1],一旦疲劳裂纹较大,进入失稳扩展阶段就可能造成构件的迅速失效,甚至造成结构整体坍塌。因此,对钢桥面板的早期疲劳裂纹损伤检测对于保障桥梁的结构安全尤为重要。
Lamb波技术因其传播距离远、检测范围广、对内部损伤敏感等特点已经被广泛用于板状结构研究和应用[2-3]。然而,线性Lamb波技术对于小于其波长的微裂纹不敏感,近年来,非线性Lamb波理论引起了众多研究者的关注。一方面由于材料非线性的影响,板状结构中能够激发出二次谐波响应,这种理论被称为经典非线性理论[4]。周正干等[5]总结了谐波产生与有限幅度法的原理与具体步骤;阎红娟等[6]通过非线性超声测量GH4169高温合金板材疲劳弯曲试验,发现随着疲劳寿命的增加,相对非线性系数单调增加。另一方面,疲劳裂纹等局部缺陷因存在非线性相互作用,也将导致Lamb波发生畸变,产生谐波成分,被称为声接触非线性理论[7-9]。阎红娟等[10]建立微裂纹非线性弹簧模型研究金属板中微裂纹长度和宽度对非线性系数的影响。张闯等[11]对铝板上的闭合裂纹进行电磁加载,建立电磁加载下金属闭合裂纹的三维有限元模型并引入非线性弹簧模型。Wang等[12-13]建立“呼吸”裂纹的二维和三维解析模型,定量研究微裂纹参数的影响,并定义了新的非线性指标。Shen等[14]采用局部交互模拟方法研究“呼吸”裂纹处Lamb波的非线性散射和模态转换现象。因此,目前对于Lamb波在疲劳裂纹处的声接触非线性研究主要集中在理论和数值研究方面。
基于声接触非线性理论,研究了非线性Lamb波在钢桥面板早期疲劳裂纹损伤检测中的效果,建立了疲劳裂纹的非线性弹簧数值模型,并利用高能超声检测系统进行非线性Lamb波的步进式扫描,研究了宏观缺陷和疲劳裂纹对能量、声速和非线性参数3个指标的影响。
1 Lamb波接触非线性原理
1.1 钢板中的Lamb波
超声波在板状结构中由于受边界的影响,横波和纵波经过反复反射和叠加形成Lamb波。在各向同性板状结构中,Lamb波有对称模式(S模态)和反对称模式(A模态)两种基本模式,它们的性质随频率的变化而变化,通过Rayleigh-Lamb方程可以求得Lamb波的频散关系[15]。
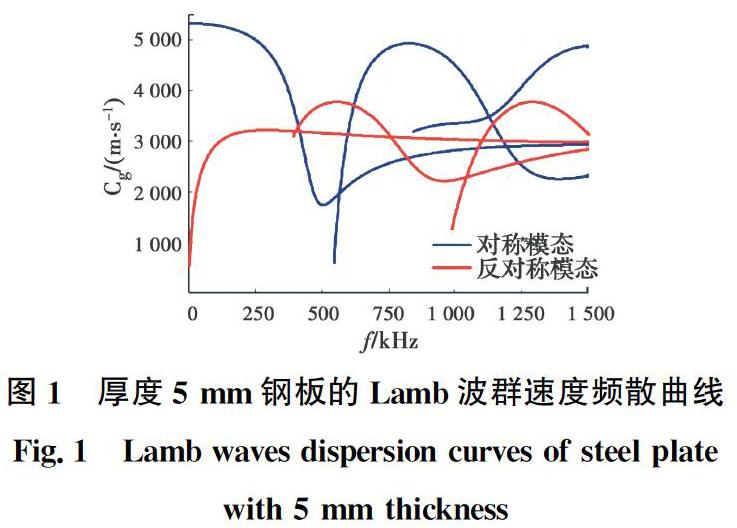
根据Rayleigh-Lamb方程绘制所用的5 mm厚度钢板的Lamb波群速度频散曲线,由图1可知,在250 kHz时,钢板中可能存在A0和S0两种模态,其中,A0模态的理论群速度为3 206 m/s,S0模态的理论群速度为5 008 m/s。
1.2 疲劳裂纹的声接触非线性
疲劳裂纹在振幅达到一定程度的循环荷载作用下可能呈现开闭交替的状态,这种状态被形象地称为“呼吸效应”,这使得钢板中的Lamb波传播到疲劳裂纹附近时与其发生局部非线性相互作用,导致波形发生畸变,出现二次甚至高次谐波[12]。
呼吸裂纹接触面上承受的内应力用一维简化模型可以表示为
式中:E是弹性模量;β为二阶弹性系数;σ和ε分别表示应力、应变。
忽略式(1)中二阶项以上的高阶项,并利用质点位移和应变的关系,代入一维波动方程后可得
式中:u为位移;ρ为介质的密度;x为波传播的距离;t为时间;c为波速。
基于微擾理论,假定位移u由线性响应ul和非线性响应unl组成
综合应用多尺度法和试解法,并在解的过程中忽略高阶小量,可以得到式(2)的近似解析解为
式中:k为波数;ω为角频率;U1和U2分别代表基波和二次谐波幅值,且存在关系
因此,β可以作为描述介质非线性的一个参数,并定义非线性参数β0为
实际上,疲劳裂纹表面的受力非常复杂,上述一维简化模型很难精确地表示疲劳裂纹的非线性相互作用过程,但不同理论最终推导的非线性参数均可表示为式(5)的形式[16],因此,选择非线性参数β0作为疲劳裂纹的主要表征参数。
1.3 接触问题的罚函数法及弹簧模型
罚函数法已被作为有限元中模拟接触问题的主要方法,其核心思路是通过一个无约束问题逼近一个约束问题,且该问题的解收敛于原约束问题的解。
图2表示了使用罚函数法近似接触连续介质力学的整个过程。此运动学中加强了不可穿透条件,即
这意味着两个物体a1和a2不能相互穿透,相互接触时边界上的点在运动过程中结合。接触面b定义为
a1和a2不接触时可被视为单独的系统,而接触时仅受接触压缩作用。为满足接触面上的交替边界条件,可以使用不连续网格来模拟裂纹表面,接触节点上引入接触刚度kc,通过惩罚接触力约束接触运动,以实现交替边界条件建模,利用罚函数法削弱不可穿透条件,并允许少量的渗透δ来违反不可穿透条件。当达到适当的接触刚度时穿透量接近零,数值解向物理接触收敛[17]。
2 试验方案与数值模型
2.1 试验设计
试件采用Q345钢板,密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3,屈服强度为345 MPa。如图3所示。试件尺寸为300 mm×120 mm×5 mm,中间预制椭圆形孔洞缺陷,两边各切割形成宽度为0.5 mm,长度为7.5 mm的宏观裂纹。在大连理工大学振动与强度测试中心进行疲劳加载试验,宏观裂纹两端各形成长度分别为16.8、9.0 mm的疲劳扩展裂纹。
为了研究非线性参数与疲劳裂纹的关系,进行步长为2 mm的步进式扫描实验,试验中采用非线性高能超声测试检测系统(RAM-5000 SNAP)输出激励和接收响应信号;激励和接收探头均采用直径为25 mm的超声换能器,位于待测钢板试样的两侧,距中线同为40 mm,步进方向如图4(a)。激励信号采用中心频率250 kHz的十周期正弦调制信号,由RAM-5000 SNAP主系统激发,经由衰减器、低通滤波器到达谐振频率250 kHz的发射探头;为了更好地探测二次谐波响应,接收端采用谐振频率500 kHz的超声探头;接收探头直接返回至主系统信号为基波信号,由于收到的信号基频幅值是倍频的10~100倍,故在接收电路中设置500 kHz带通滤波器分离出二次谐波信号,实验装置连接方式如图4(b)。
2.2 有限元模型
基于商业有限元ANSYS建立钢板试件的三维实体模型,钢板采用Solid45实体单元。在裂纹位置对模型进行切分,形成不连续网格,对于无损伤位置的节点进行自由度耦合,而宏观裂纹处则形成自由界面,如图5(a)所示。为模拟疲劳裂纹的“呼吸效应”,在疲劳裂纹位置的相应节点间添加Combine39非线性弹簧单元,弹簧单元采用如图5(b)所示力位移曲线,即采用单向受压弹簧在裂纹界面之间只传递压应力而不传递拉应力,故弹性的受压刚度系数需要足够大但同时不引起数值不收敛现象,经过调试设置弹簧受压刚度选择为2×108 N/m。
数值模拟采用与试验方案相同的中心频率250 kHz的十周期正弦调制荷载,根据波长设置有限元网格最大尺寸为2 mm。按照试验的步进式扫描方案,在发射端相应位置的节点上沿x -y平面施加8个不同方向的位移荷载,并在接收端相应位置提取z方向的位移作为接收响应信号。
需要注意的是,数值模拟并不能完全模拟实验过程,主要区别在于:简化的闭合裂纹模型并不能精确反映疲劳裂纹的复杂受力过程;为了保证模型的收敛性,数值模型施加的荷载方向与试验中探头的发射方向不一致,可能导致激发的Lamb波模态不同;试验中的探头直径为25 mm,接收信号为平均响应,且发射和接收的是电信号,而数值模拟中施加和接收的都是结构上具体点的位移响应。然而,数值模型仍然能够有效地反映钢板中Lamb波与疲劳裂纹的相互作用机理,可以用来验证损伤指标随宏观缺陷和疲劳裂纹的变化规律。
3 结果分析与讨论
3.1 疲劳裂纹的影响
在数值模拟中提取的步进8 mm位置(无损伤)和步进20 mm位置(含疲劳裂纹)的位移响应结果如图6所示。无损伤路径的拟声速为4 762 m/s,而含疲劳裂纹路径的为4 734 m/s,两者的拟声速变化不大,且与频散曲线中S0模态的理论声速(5 008 m/s)非常接近,因此,数值模拟中主要激发出S0模态。与无损伤路径结果进行对比,其首波幅值略微减小,且受闭合裂纹影响,导致其首波信号出现明显的波形畸变,同时,幅频图中明显出现二倍频(500 kHz)及三倍频(750 kHz)。
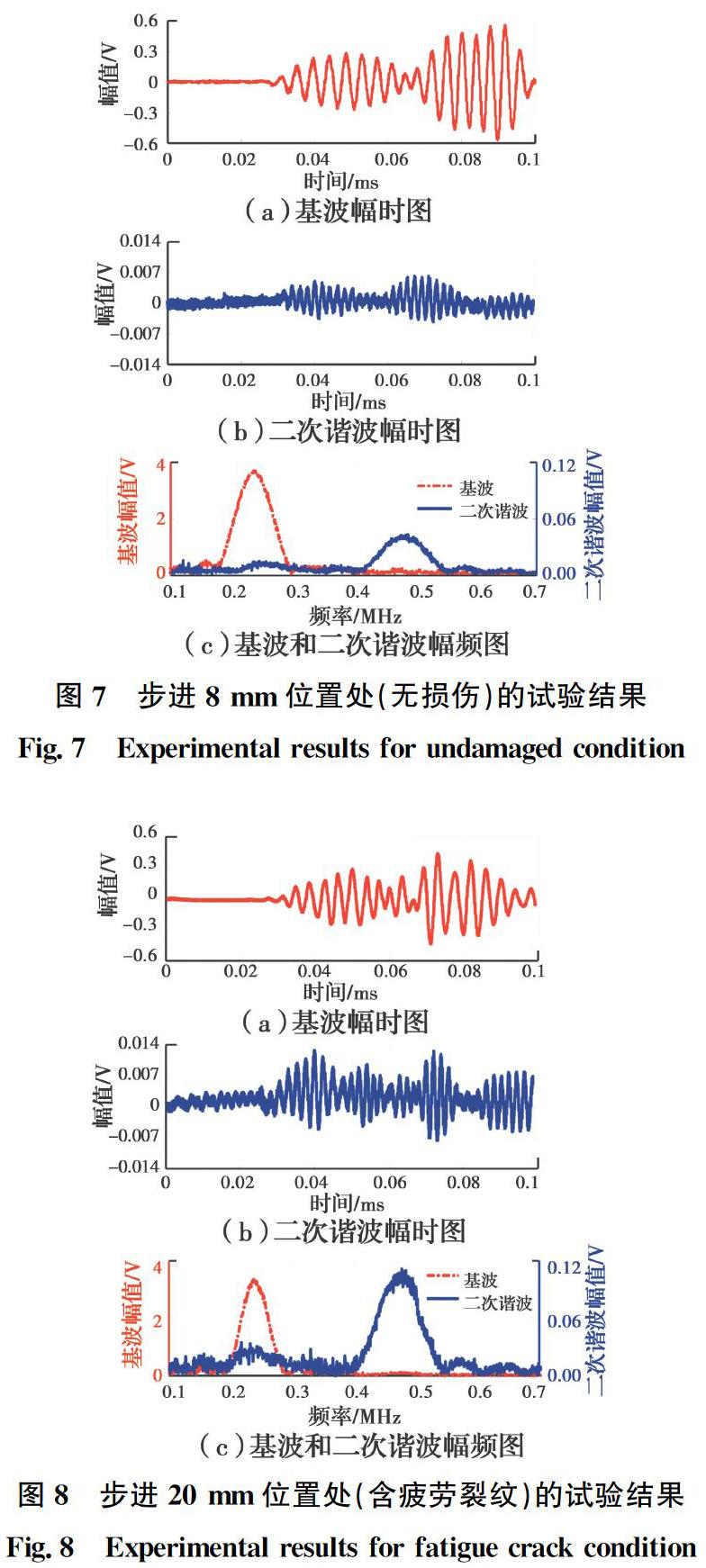
图7和图8分别给出了无损伤路径(步进8 mm位置)和含疲劳裂纹损伤路径(步进20 mm位置)的试验结果。无损伤路径和含疲劳裂纹损伤路径的基波幅值相差不大,同时,拟声速分别为3 030、2 827 m/s,两者也相差不大。且与频散曲线中A0模态的理论声速(3 206 m/s)接近,因此,试验中主要以A0模态为主。与数值模拟结果不同的是,试验中含疲劳裂纹损伤路径的基波并无可见的波形畸变,在基波频谱图中也看不到倍频尖端,说明实际检测中二次谐波信号远不如理想化数值模型中明显。因此,试验中通过500 kHz带通滤波器捕捉二次谐波信号,如图7(b)和图8(b)所示。根据基波和二次谐波的频谱图可知,基波频谱峰值在238 kHz左右,而二次谐波频谱峰值在473 kHz左右,虽然中心频率稍有改变,但仍成倍数关系。无损伤路径上的基波幅频峰值为3.65 V,二次谐波幅频峰值为0.038 V,计算其非线性参数为2.85×10-3,此时的二次谐波主要由材料非线性引起[10]。而含疲劳裂纹的路上的基波幅频峰值为3.38 V,二次谐波幅频峰值为0.11 V,计算其非线性参数为9.63×10-3,可见,由于疲劳裂纹的局部非线性导致其非线性参数显著增大。
3.2 宏观缺陷的影响
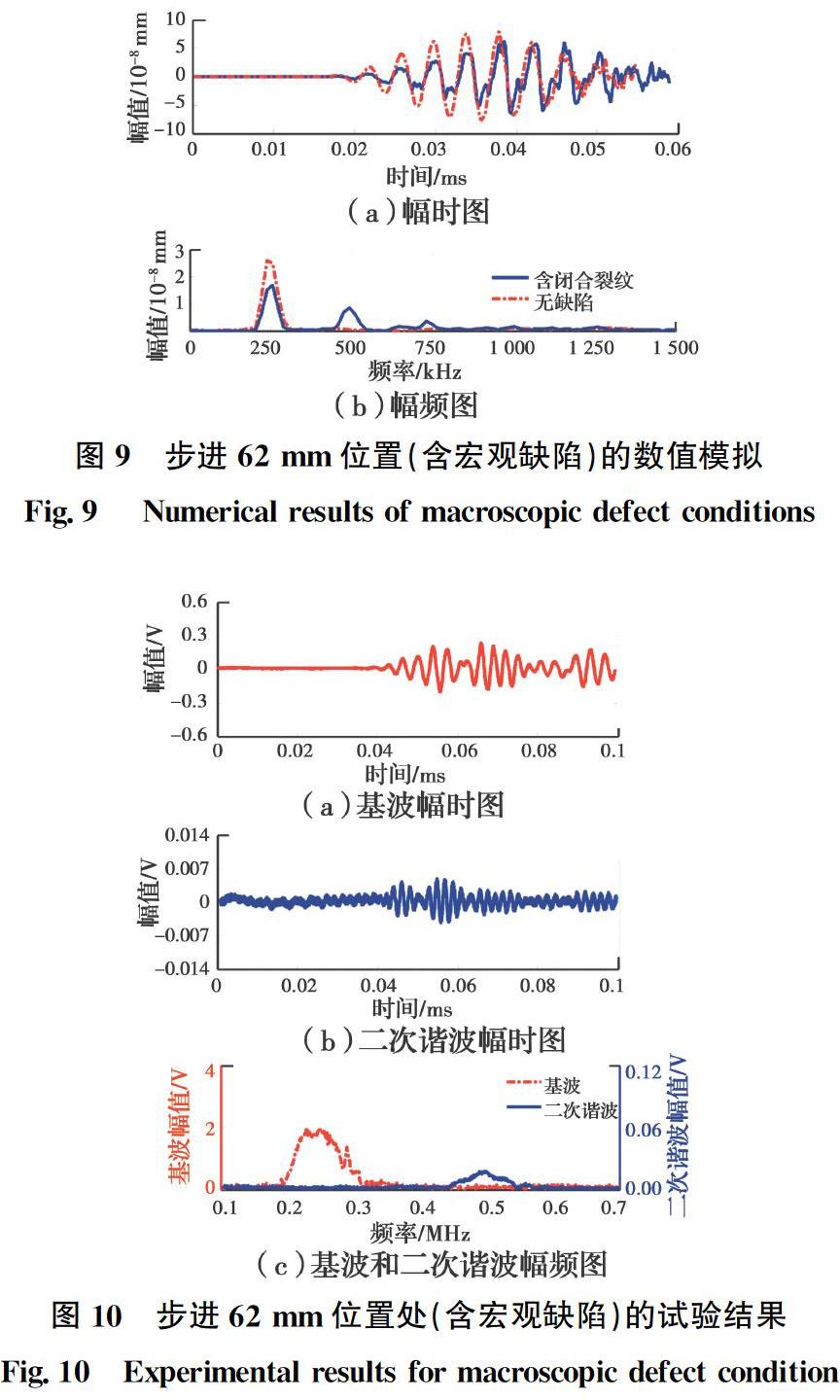
在数值模拟中提取的步进62 mm位置(含宏观缺陷)的位移响应结果如图9所示。其首波幅值和拟声速(2 312 m/s)与无损伤情况均显著较小,因为Lamb波在宏观缺陷处发生严重的反射和散射,并且宏观缺陷大于波长,导致Lamb波传播路径发生改变而需绕过宏观缺陷到达接收点。此时可通过信号首波能量和拟声速变化识别宏观缺陷。
试验研究中含宏观缺陷路径的检测结果如图10所示。与无损伤的路径相比,其幅值和拟声速(2 062 m/s)均显著下降。通过频谱图可知其基波幅频峰值为1.86 V,二次谐波幅频峰值为0.018 V,计算其非线性参数为5.2×10-3,其非线性参数大于无损伤路径可能是因為超声波绕过宏观缺陷时受到了疲劳裂纹的影响,同时,其非线性参数仍明显小于含疲劳裂纹路径的非线性参数。
3.3 损伤识别和定位
图11给出了数值模拟中首波能量、拟声速和变化曲线非线性参数随步进位置变化曲线。首波能量和拟声速随步进位置变化趋势相近,即在模型中部的宏观裂纹及孔洞位置处显著减小,但在含闭合裂纹处变化相对不明显;而非线性参数在通过含闭合裂纹的路径会明显增大,且裂纹尖端处比闭合裂纹尾端处的非线性参数值大。可以初步定位宏观缺陷位置为距板上边界32.5~87.5 mm、闭合裂纹缺陷位置为距钢板上边界15.7~32.5 mm及87.5~98.2 mm,识别误差为6%。
图12给出了试验研究首波能量、拟声速和非线性参数随步进位置变化曲线,其中首波能量和拟声速包括基波和二次谐波的结果。基波的首波能量在疲劳裂纹处变化不大,而在宏观路径上显著减小;但二次谐波的首波能量在疲劳裂纹处显著增大。试验中基波和二次谐波的拟声速在疲劳裂纹处轻微减小,而在宏观裂纹处显著减小。非线性参数在疲劳裂纹处显著增大,而在宏观缺陷处的非线性参数略大于无损伤路径。
因此,上述数值模拟和试验结果对损伤识别的效果基本一致,综合考虑首波能量、拟声速和非线性参数可以实现宏观缺陷和疲劳裂纹损伤类型的识别和大致损伤区域的定位。
4 结论
对钢板的非线性导波检测进行数值模拟和试验研究,分析宏观缺陷和疲劳裂纹影响下的首波能量、拟声速和非线性参数随步进位置的变化规律,实现了钢板中宏观缺陷和疲劳裂纹的识别与定位,获得如下主要结论:
1)基于非线性弹簧的闭合裂纹模型可以有效地反映钢桥面板中导波与疲劳裂纹的接触非线性相互作用机理,疲劳裂纹处的局部非线性导致Lamb波信号发生畸变,二倍频甚至三倍频谐波成份显著增大。但在实际试件中,二次谐波响应不易直接观测,需要利用带通滤波器提取二次谐波响应。
2)当钢桥面板中出现疲劳裂纹,由于裂纹处的声接触非线性效益,导致非线性参数和二次谐波能量显著增大,而基波首波能量和拟声速几乎不发生改变。
3)当钢桥面板中出现宏观缺陷时,导波在损伤界面上发生反射,导致基波能量明显减小;当宏观缺陷明显大于波长时,波的传播路径发生改变,导致拟声速明显减小;但宏观缺陷几乎不改变信号的非线性参数和二次谐波能量。
参考文献:
[1] MEYENDORF N G H, RSNER H, KRAMB V, et al. Thermo-acoustic fatigue characterization [J]. Ultrasonics, 2002, 40: 427-434.
[2] BAHADOR M M, ZAIMBASHI A, RAHGOZAR R. Three-stage Lamb-wave-based damage localization algorithm in plate-like structures for structural health monitoring applications [J]. Signal Processing, 2020, 168: 107360.
[3] XU C B, YANG Z B, TIAN S H, et al. Lamb wave inspection for composite laminates using a combined method of sparse reconstruction and delay-and-sum [J]. Composite Structures, 2019, 223: 110973.
[4] MLLER M F, KIM J Y, QU J M, et al. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates [J]. The Journal of the Acoustical Society of America, 2010, 127(4): 2141-2152.
[5] 周正干, 劉斯明. 非线性无损检测技术的研究、应用和发展[J]. 机械工程学报, 2011, 47(8): 2-11.
ZHOU Z G, LIU S M. Nonlinear ultrasonic techniques used in nondestructive testing: A review [J]. Journal of Mechanical Engineering, 2011, 47(8): 2-11. (in Chinese)
[6] 阎红娟, 刘峰斌, 潘勤学. GH4169高温合金疲劳寿命非线性超声检测研究[J]. 机械设计与制造, 2019(2): 127-130.
YAN H J, LIU F B, PAN Q X. GH4169 superalloy fatigue life detection using nonlinear ultrasonic [J]. Machinery Design & Manufacture, 2019(2): 127-130. (in Chinese)
[7] KROHN N, STOESSEL R, BUSSE G. Acoustic non-linearity for defect selective imaging [J]. Ultrasonics, 2002, 40(1-8): 633-637.
[8] SOLODOV I Y, KROHN N, BUSSE G. CAN: an example of nonclassical acoustic nonlinearity in solids [J]. Ultrasonics, 2002, 40: 621-625.
[9] SOLODOV I Y. Ultrasonics of non-linear contacts: propagation, reflection and NDE-applications [J]. Ultrasonics, 1998, 36: 383-390.
[10] 阎红娟, 刘峰斌, 潘勤学. 金属板件中微裂纹的非线性超声表征方法研究[J]. 现代制造工程, 2018(4): 17-21.
YAN H J, LIU F B, PAN Q X. Characterization of micro-crack in metal plane using nonlinear ultrasonic waves [J]. Modern Manufacturing Engineering, 2018(4): 17-21. (in Chinese)
[11] 张闯, 庞文英, 刘素贞, 等. 电磁加载下铝板闭合裂纹的动态特性分析[J]. 中国电机工程学报, 2018, 38(7): 2171-2178, 2232.
ZHANG C, PANG W Y, LIU S Z, et al. Dynamic characteristics analysis of closed cracks in aluminum plate under electromagnetic loading [J]. Proceedings of the CSEE, 2018, 38(7): 2171-2178, 2232. (in Chinese)
[12] WANG K, LI Y H, SU Z Q, et al. Nonlinear aspects of "breathing" crack-disturbed plate waves: 3-D analytical modeling with experimental validation [J]. International Journal of Mechanical Sciences, 2019, 159: 140-150.
[13] WANG K, LIU M L, SU Z Q, et al. Analytical insight into "breathing" crack-induced acoustic nonlinearity with an application to quantitative evaluation of contact cracks [J]. Ultrasonics, 2018, 88: 157-167.
[14] SHEN Y F, CESNIK C E S. Nonlinear scattering and mode conversion of Lamb waves at breathing cracks: an efficient numerical approach [J]. Ultrasonics, 2019, 94: 202-217.
[15] ROSE J L. Ultrasonic guided waves in solid media[M]. New York: Cambridge University Press, 2014.
[16] DENG M X. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach [J]. Journal of Applied Physics, 2003, 94(6): 4152-4159.
[17] SHEN Y F, CESNIK C E S. Modeling of nonlinear interactions between guided waves and fatigue cracks using local interaction simulation approach [J]. Ultrasonics, 2017, 74: 106-123.
(编辑 章润红)
