HPM课例研究对教师MKT的影响

栗小妮，汪晓勤

HPM课例研究对教师MKT的影响

栗小妮，汪晓勤

（华东师范大学 教师教育学院，上海 200062）

HPM课例研究流程包括选题与准备、研讨与设计、实施与反馈、整理与写作．以HPM视角下“有理数乘法”的课例研究为载体，通过分析HPM工作室8位在职教师课例研究过程中的3版教学设计、2份反思和问卷调查发现：HPM课例研究可以促进授课教师的专业发展；课例研究的4个环节对教师MKT各部分的影响不同：在“选题与准备”环节，主要对教师的SCK和KCT产生影响；在“研讨与设计”环节，主要影响SCK、HCK和KCT；在“实施与反馈”环节，主要影响KCS和KCT；研讨是课例研究的核心环节；异质人员参与课例研讨可以深化拓展教师MKT的改变．

课例研究；数学史与数学教育；有理数乘法

1 问题提出

课例研究被认为是“改变21世纪教师专业发展的强有力途径”[1]．已有研究表明：课例研究作为一种改进课堂教学质量、促进教师专业学习的实践方式，有助于实践共同体内教师专业知识的扩充，专业能力的提升，专业态度的强化，专业学习环境的形成，专业发展层次的提高等．但同时也存在一些问题，如人员缺乏异质性．外部专家的支持，不同立场、不同层次教师的沟通对话有助于促进教师的反思等[2]．

自从1972年，第二届国际数学教育大会上成立数学史与数学教学关系国际研究小组（International Study Group on the Relations between History and Pedagogy of Mathematics）以来，HPM作为数学教育的一个新兴领域，越来越受国内外数学教育者的关注．HPM的研究从最初的“为何”“如何”等的理论探讨逐渐转向HPM视角下的数学教学设计与实践的研究[3]．已有的国内外教学实践研究均已证实数学史对于教师的知识（如MKT）、信念等方面具有促进作用[4-10]，但这些研究中的研究对象仅局限于职前教师或者是进行HPM视角下教学设计与实践的单一在职教师．对于大多数未进行过HPM视角下的教学设计与实践的在职教师而言，将数学史融入数学教育依然处于“高评价、低应用”的阶段，在职教师如何恰当并柔和地将数学史融入到教学中，最大程度地实现数学史的价值，需要在职教师深刻理解数学史料并根据学生的情况进行恰当地裁剪和运用．

怎样在一个HPM视角下的数学教学设计与实践的研究过程中影响更多的老师？以工作室为基础展开课例研究为研究者提供了新的思路．HPM工作室作为HPM实践共同体主要由高校HPM研究者和中学一线教师组成，前者可以提供数学史文献、HPM理论、教育研究方法等方面的资源，承担课例研究中异质人员的作用，而一线教师则对教材和学生更为熟悉，是HPM研讨课设计和实施的主要参与者．因此，研究者将研究问题确定为：HPM课例研究对HPM工作室中所有在职教师的MKT会产生哪些影响？高校HPM研究者作为共同体中的异质人员起什么作用？

2 MKT与HPM联系的研究

随着HPM研究的逐渐深入，有研究者认为数学史融入数学教学的研究缺乏与一般数学教育研究的理论框架、方法之间的联系[11]．HPM的研究要想在普通数学教育研究中更有影响力，就必须与一般数学教育研究中的理论框架建立联系，如与MKT建立联系[12]．所谓MKT（Mathematical Knowledge for Teaching）指的是“面向教学的数学知识”，最早由密歇根大学的Ball团队提出，其组成成分如图1[13]．

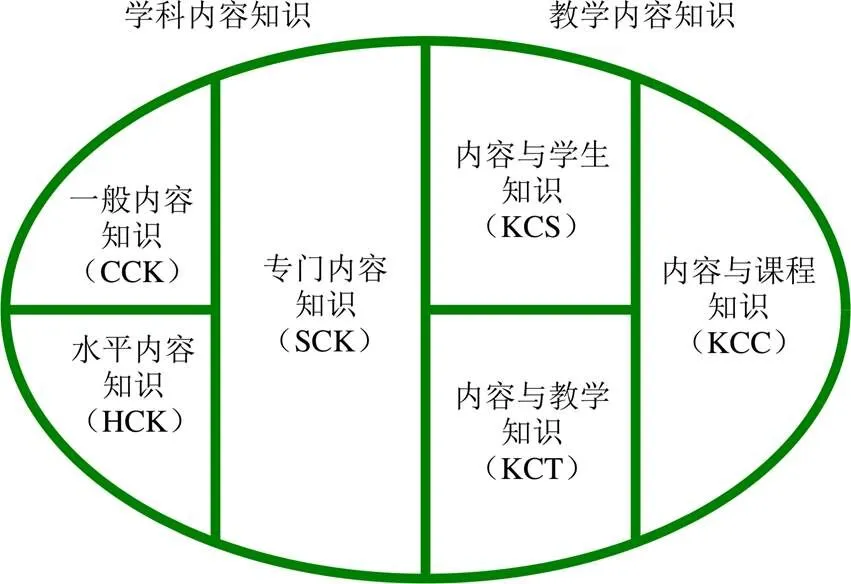
图1 MKT的结构

“一般内容知识”是指除教学外，在其它背景下也使用的数学知识和技能；“专门内容知识”是指教学所特有的数学知识和技能；“水平内容知识”是关于整个数学课程中数学主题之间联系的知识；“内容与学生知识”是指对学生的了解和对数学的了解相结合的知识；“内容与教授知识”是指对如何教授的了解和对数学的了解相结合的知识；“内容与课程知识”是指关于课程大纲、课程标准、教科书、教学材料以及其它教学资源的知识．

已有研究表明，数学史对教师的MKT有促进作用．如美国学者Clark通过融入数学史的教学，促进了职前师范生对自己和自己未来学生解决一元二次方程问题的认识．同时，他也呼吁需要对数学史如何促进教师对知识的深刻理解做进一步的研究[14]．意大利学者Fenaroli等在一项为期2年、针对职前中学教师开展的数学史课程项目中发现，数学史可以促进职前中学教师对关键数学概念的理解[15]．在此基础上，Jankvist等通过对3个典型的案例进行分析，进一步说明了数学史对于教师MKT的促进作用，可以采用MKT的框架说明数学史对教师知识方面的发展[12]．Mosvold等利用文献说明数学史可以用来验证MKT的每个部分，一些数学史的例子还可以用来说明MKT中的每一部分并没有严格清晰的界限[16]．同时，也有研究提到，在现有的MKT理论中，很少涉及数学史的内容，对HPM与MKT联系的研究有助于完善MKT理论[17]．综上可知，已有的关于HPM与MKT的研究主要聚焦于职前师范生，较少关注在职教师．

3 研究设计

3.1 研究对象

采用自愿参与的原则，在课例研究前已向所有工作室的初中数学教师讲明所要参与研讨、观课的时间，所要提交的材料和时间节点．所以，作为研究对象的8位初中数学教师，均能真实表达各自的想法，保证了研究的信度．他们的基本情况如表1所示．

其中，除教师T5在工作室成立之前，曾与大学HPM研究人员合作开发过HPM课例，对HPM有一定的认识外，其他教师均是第一次接触HPM．表1中所有教师均全程参与了课例研究．所研究的主题为沪教版初中七年级“有理数乘法”一节，在本节课中学生学习有理数乘法法则，并能够简单应用法则进行计算．在此之前，所有教师均未接触过有理数乘法法则的历史．已有的调查研究表明，让学生接受有理数乘法法则，特别是“负负得正”不难，但让学生理解为什么“负负得正”是很困难的[18-19]．研究的目的就在于在合理运用数学史料让学生理解为什么“负负得正”．

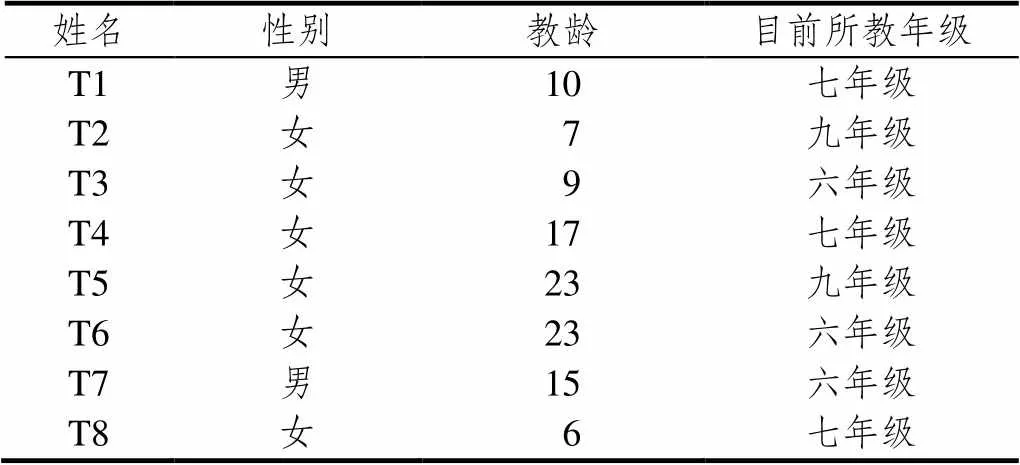
表1 研究对象基本情况

3.2 HPM课例研究流程

已有HPM课例研究流程主要由4部分组成，选题与准备、研讨与设计、实施与反馈、整理与写作[20]．首先，选择历史脉络清晰的主题，高校研究者对相关主题进行深入研究后，将相关历史素材提供给在职教师；其次，在职教师根据史料进行教学设计并与高校研究者进行研讨，修正教学设计；再次，进行2~3次的试讲后，教师进行观摩课教学，并实施课后学生问卷调查；最后，教师进行教学实录，结合学生问卷反馈和自己的反思，完成课例报告的撰写和分享．结合HPM工作室的特征，对已有的HPM课例研究流程进行了一些调整，如图2所示．

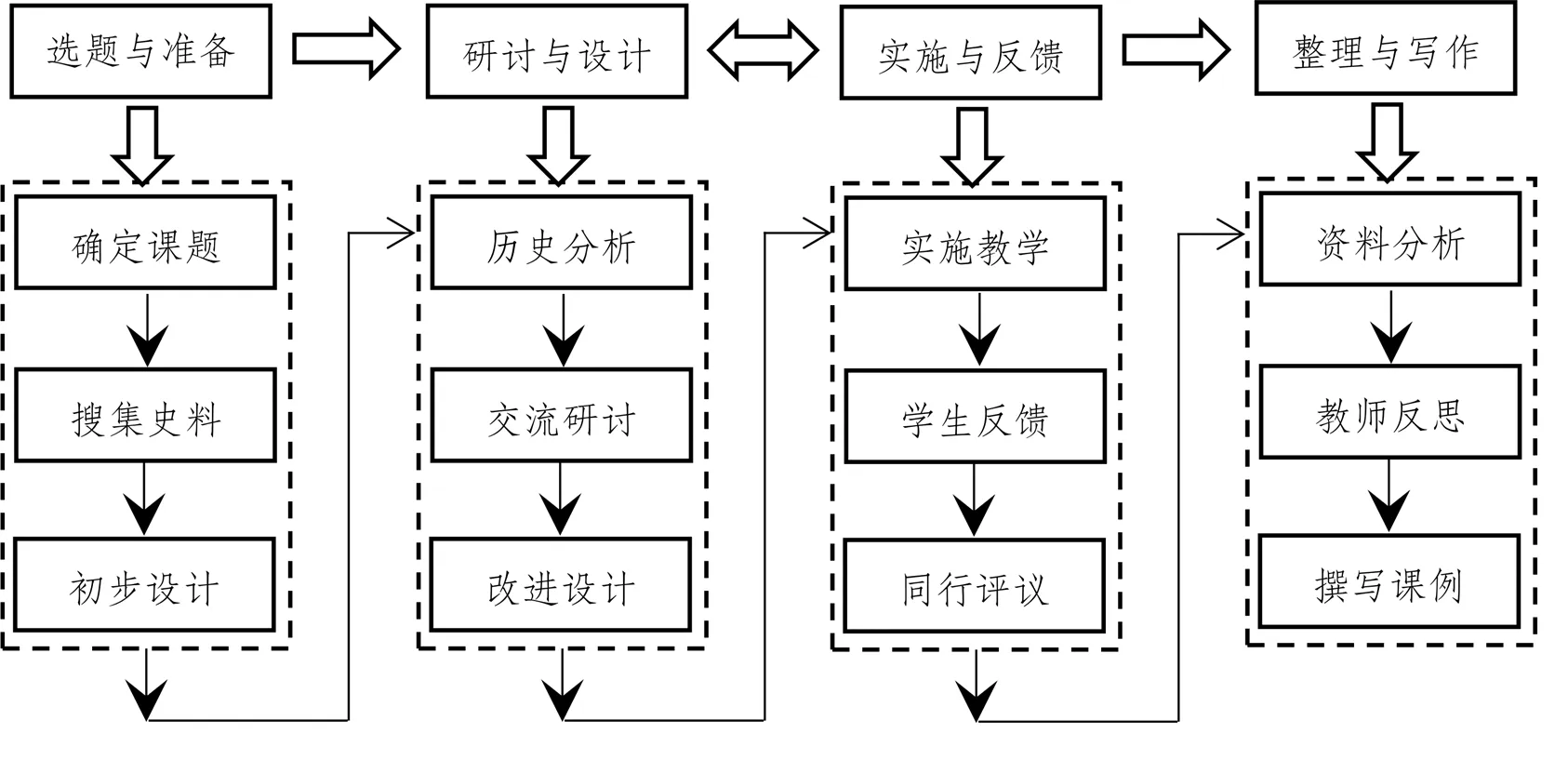
图2 HPM课例研究的流程

“选题与准备”阶段：工作室教师在拿到相关历史材料后，自行阅读，并根据自己对史料的理解，结合已有的教学经验，进行初步融入数学史的教学设计．教学设计要求教师写明每一环节的设计意图，包括所选择的史料拟实现的价值等．同时确定一位研讨课的授课教师．

“研讨与设计”阶段：选择合适的时间，进行共同体内的研讨．研讨分以下几个环节：

（1）高校研究者简要解读相关史料；

（2）研讨课的授课教师汇报自己的教学设计，以及阐述运用史料进行教学设计过程中出现的问题或者困惑；

（3）教师简述自己已有的教学方式，所有成员根据教学目标和HPM的理念，对教学设计进行研讨，提出修改意见或建议．

会后，根据研讨的收获，工作室内的教师对自己的教学设计进行反思和修改．

“实施与反馈”阶段：增加了“同行评议”环节，课后所有参与观摩的教师进行评课反思和再次研讨．研讨的内容主要分为两方面：（1）结合自己的教学设计，谈谈研讨课教学目标是否达成，研讨课的亮点和不足；（2）本节课数学史的融入是否合适，实现了哪些价值？

3.3 数据收集

在HPM课例研究的过程中进行数据收集，并对所收集的资料进行编码．收集的资料包括教师的3份教学设计、2份反思报告和1份调查问卷．

教学设计包括：（1）教师在进行课例研究前，提交一份自己曾经采用的有理数乘法法则教学设计1（编码为s1）；（2）在“选题与准备”阶段，教师在自行阅读相关历史材料后，独自进行融入数学史的教学设计2（编码为s2）；（3）“研讨与设计”阶段，经过高校研究者对历史材料的解读以及工作室成员对教学设计研讨后，教师经过反思对教学设计2进行修改，得到教学设计3（编码为s3）；

反思报告包括：（1）“研讨与设计”阶段，教师参加集中研讨后的反思1（编码为r1）；（2）在“实施与反馈”阶段，教师观摩研讨课后的评课反思2（编码为r2）．

问卷调查为课例活动结束后的补充调查，调查教师在反思报告中未谈到的MKT的分支部分，如部分教师会在反思中提及对后续教学的启示，部分教师在反思中未提及，这涉及教师MKT中KCT部分的变化．所以调查问题包括；①阅读有关负数和有理数乘法法则的历史，您有哪些收获（补充调查“选择与准备”环节教师的收获，作为反思1的补充）？②如果您再上“有理数乘法”这节课，您觉得在教学中要注意什么（补充调查教师KCT的变化，作为反思2的补充）？表2为课例研究流程中数据收集的节点．

表2 数据收集节点

两名研究人员对所收集的材料进行研讨和分析，讨论确定所收集的数据属于教师MKT哪个部分的变化，确保研究的效度．

4 有理数乘法的历史和解释模型

研究者提供给教师的历史素材主要包括两部分：一是负数和有理数乘法法则的历史以及一些历史名人学习“负负得正”的困惑；二是教科书以及历史上曾出现的解释有理数乘法法则的模型．

4.1 有理数乘法法则的历史

负数的概念最早出现在中国，是由于解方程组的消元过程中出现了“不够减”的情形．公元7世纪印度数学家婆罗摩笈多（Brahmagup-ta）也明确提出了正负数的概念及其四则运算法则：“正负相乘得负，两负数相乘得正，两正数相乘得正．”公元13世纪末，中国数学家朱世杰在《算学启蒙》（1299）中给出负数的乘除法则“明乘除法，同名相乘得正，异名相乘得负”．但负数及其运算法则在西方却出现得较晚，直到18世纪，还有一些西方数学家不理解“小于一无所有的数”，并认为“负负得正”这一法则是个谬论．甚至在19世纪，英国还有数学家不接受负数[20]．

在19世纪中叶以前，负数概念以及“负负得正”的运算法则在学校代数课本中并没有得到正确的解释，有很多名人都曾对“负负得正”感到困惑，并由此而影响了他们对数学的根本看法．如法国著名昆虫学家、文学家法布尔（C. Fabre，1823—1915）在学习“负负得正”时吃尽了苦头．法国著名作家司汤达（Stendhal，1783—1843）也曾不理解“负负得正”，希望老师能对“负负得正”作出解释，但他的老师不管怎么解释，总不能让司汤达信服．最后老师用债务做比喻，但却让司汤达更困惑了：“一个人该怎么把1 000法郎的债与500法郎的债乘起来，才能得到500 000法郎的收入呢？”老师只好搬出大数学家欧拉（L. Euler，1707—1783）与拉格朗日（Lagrange，1736—1813）来：这些大数学家都用得理所当然，你又何必钻牛角尖呢？万般无奈下，司汤达只好接受了它，但这个学习经历一度动摇了他对数学和数学教师的信心[21]．

4.2 有理数乘法法则的解释模型

对于有理数乘法法则的解释模型，研究者提供给教师的主要有以下7类（如表3）．

表3 有理数乘法法则的解释模型

故事模型的另一种表述方式为：好孩子用正数表示（＋），坏孩子用负数表示（－）；进城用正数表示（＋），出城用负数表示（－）；好事用正数表示（＋），坏事用负数表示（－）．好孩子（＋）进城（＋），对城市来说是件好事（＋），所以（＋）×（＋）＝＋；坏孩子（－）出城（－），对城市来说是件好事（＋），所以（－）×（－）＝＋．

欧拉在《代数基础》中也对“负负得正”做出了自己的解释，可归为“相反数模型”．他首先通过债务的倍数来说明正负得负：由于(-)×(-)（>0,>0）要么等于，要么等于-，但前面已经证明(-)×=-，而(-)×(-)不可能与(-)×的结果相同，故只能有(-)×(-) =．因此有负负得正[29]．

上述每一种模型，都只能算是有理数乘法法则的一种解释，正负得负、负负得正都是在数系扩充过程中，为保证在正数范围内的运算律依然成立的必然结果，无法证明，但可以用现实模型进行合理解释．正如大数学家F·克莱因（F. Klein，1849—1925）所说：“不要试图去证明符号法则的逻辑必要性，别把不可能的证明讲得似乎成立．”[30]

5 研究结果

5.1 教学设计的比较

数学的新授课一般分为引入、探究、巩固和小结4个环节．引入环节主要是创设符合学生认知起点的情境，引入即将要学习的知识．探究环节是学生以小组为单位，利用教师所提供的情境，在教师的引导下，探究得出所要学习的知识；巩固环节是通过一定的练习熟悉所学知识，最后师生通过回忆，归纳小结所学知识、思想方法．巩固环节主要为练习．小结环节要根据具体上课的情形进行归纳总结．所以，从教学设计而言，前两个环节是差异较为突出的部分，研究者主要比较教师所设计的教案中引入和探究两个环节．

通过3版教学设计的比较，发现在进入工作室之前，即教师尚未接触相关数学史料之前，教师不太关注有理数乘法的解释模型，原有的教学设计s1基本与教科书中的一致，通常会花5~10分钟时间进行法则的解释，然后将剩余的时间用于巩固练习．所以，研究者主要比较研讨前和研讨后教师的两版教学设计s2和s3，表4为8位教师两版教学设计在引入环节采用方式的比较，表5为8位教师两版教学设计在探究环节所采用的模型和方式的比较，其中T3为研讨课授课教师．

表4 引入环节比较

表5 探究环节比较

这8位教师中，除T7和T8两位教师前后两版教学设计没有改变外，其余6位教师都在研讨后对教学设计进行了修改．

T1研讨后增加了司汤达的故事，并将气温测量模型进行了深入挖掘，在原有基础上，改变正负的规定，得到同样的符号法则，加深学生对法则的理解．不同的规定，不同的模型都会得到同样的结论．

T2前后两版教学设计改动较大，研讨前选用了归纳模型、运动模型和相反数模型，研讨后选用了司汤达的故事引入，然后用故事模型解释符号法则，再利用负债模型解决司汤达的困惑，在学生理解了符号法则的基础上，让学生结合自己的生活经验，解释“负负得正”的合理性，强化学生对符号法则的理解．

T3是研讨课的授课教师，在研讨时汇报了自己的初步教学设计，在研讨后改进教学设计，并实施教学．研讨前的教学设计中，她采用教科书中的相反数模型引入，在探究环节，先用欧拉的方法解释负负得正，然后选用3个不同背景的运动模型（一个人在数轴上向左或向右运动、一个人向山上或者山下运动、一辆汽车向东或者向西运动）进一步解释有理数乘法法则．在汇报时，T3提出了自己的困惑：“在读了史料后，才知道很多模型都可以用来解释‘负负得正’，但是不知道选择哪一种更合适？”从T3研讨前的教学设计中也可以看出她对模型选择的困惑，在探究环节所选择的3个模型本质上是同一类型的模型．

通过HPM研究者对数学史料的解读以及集体研讨后，T3修改了教学设计，用司汤达的故事引入，引起学生的好奇．在探究环节，先介绍负债模型，解决司汤达的困惑，然后让学生小组合作类比负债模型，用生活中的例子解释“负负得正”，再用微视频介绍历史上的其它模型，进一步深化学生对有理数乘法法则的理解．

T4研讨前的教学设计中误认为爱因斯坦的方法是在证明“负负得正”，花较大篇幅介绍了爱因斯坦解释“负负得正”的方法．研讨后，她认为爱因斯坦的方法超出了七年级学生的认知基础，且不能算是证明的话，趣味性不够，所以在得知无法证明“负负得正”后，在修改稿中删掉了爱因斯坦的方法．

T5采用翻转课堂的模式，将负债模型改编为与学生生活相关的“父母收入”模型，在课前让学生通过探究得到有理数乘法法则，课上第一环节让学生汇报有理数乘法法则，并解释(-8)×(-4)＝+32的实际意义．在研讨前的教学设计中，T5试图在第二环节通过分配律模型向学生展示如何利用分配律严格推理符号法则．在研讨后得知无法证明“负负得正”，修改了教学设计．她依然选用了分配律模型，但改为向学生介绍这个模型也可以解释“负负得正”，但在数学上不能证明“负负得正”．

研讨后，T6认为虽然学生已经学习了相反数的定义，但并未涉及一个正数乘以（-1）的符号处理，用教科书中的相反数模型来得到符号法则，存在循环论证．所以在修改后的教学设计中，她只是用教科书中的相反数模型提出问题，并不解决这个问题，用运动模型来探究法则后再解决这个问题．

5.2 教师MKT变化分析

根据MKT各部分的定义，对课例研究中教师知识的改变进行划分．教师知道有理数乘法法则，并会运用法则进行计算，这属于“一般内容知识”．知道“负负得正”可以由很多现实模型解释，知道“负负得正”并不能证明，而是一种合理的规定，这些都是教学所特有的数学知识和技能，属于教师“专门内容知识”的增加．知道负负得正的缘由以及它与已有的运算律、其它学科之间的关系，这些属于教师“水平内容知识”的增加．认识到看似简单的规定对学生而言并不简单，改变教师对学生的认识，属于教师“内容与学生知识”的增加．知道要选择适合学生的模型，通过探究让学生理解有理数乘法法则的合理性；知道用现实模型解释“负负得正”的关键在于讲清楚“正与负的分界”，这些属于教师“内容与教学知识”的增加．理解了教科书设计的意图等，这属于教师“内容与课程知识”增加．

通过对所收集数据的分析，表6为所收集的教师教学设计、反思数据与MKT各部分的关系（由于T7、T8教师教学设计3无改变，故不对他们的教学设计3做重复归类），如T1教师在s2中将教科书中的运动模型替换成了气温模型，在s3中增加了司汤达的故事，属于SCK和KCT的变化，在研讨后的反思1中她谈到：“‘负负得正’是保证原有运算律成立的合理规定，不同的正负规定，不同的模型都会得到同样的结论……研讨最大的收获是今后在运算法则课的教学中会更加关注算理的讲解，对于规定的法则会强调其合理性与必要性，而非简单的操练．”属于HCK和KCT的变化，在观课后的反思2中她谈到，“这样一个看似简单问题的探究会影响学生学习的态度，让学生知道要善于思考”，属于KCT、KCS的变化．

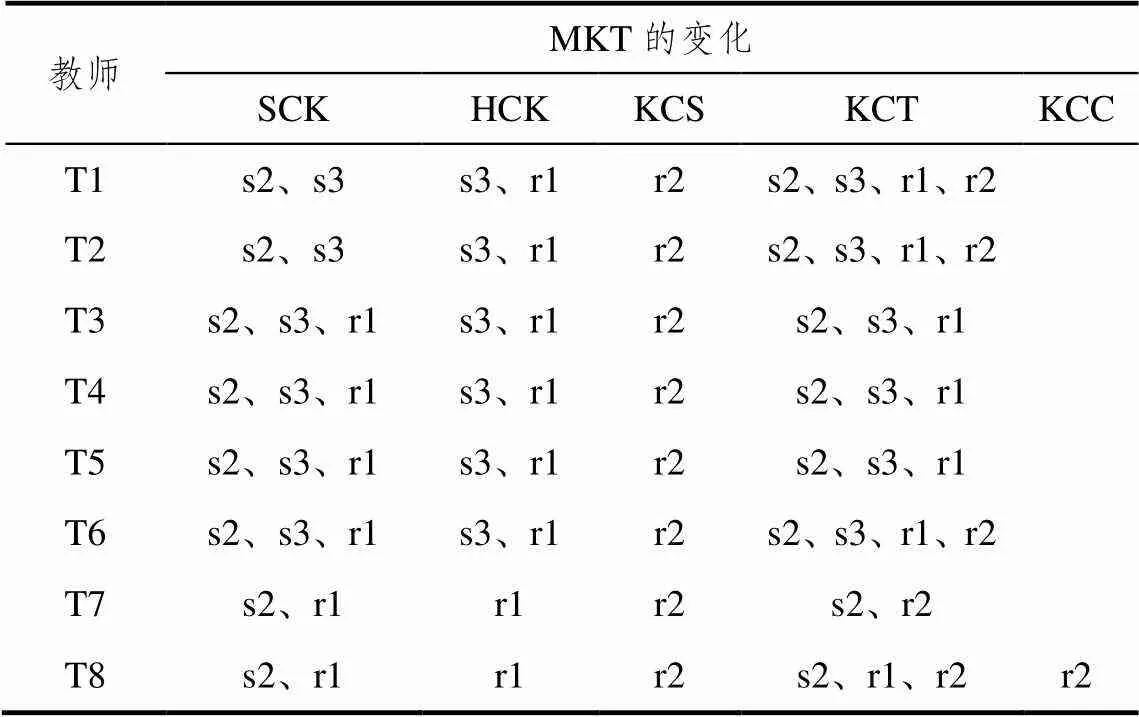
表6 8位教师MKT的变化

5.2.1 教师SCK变化分析

教师在教学设计2中对所提供的有理数乘法法则的历史和解释模型进行了初步选用，说明教师通过自行阅读史料后，初步了解了有理数乘法的解释模型和历史，SCK发生了变化．在集中研讨后，6位教师对教学设计2进行了修改，从教学设计3以及教师对研讨的反思中，可以看出教师的SCK得到了进一步的扩展和深化．以T3教师为例，阅读史料后，她在教学设计2中选用了3种模型，希望通过不同的模型增强学生对法则的理解，在研讨后，她了解到教学设计2中她所选用的3种模型本质上均属于运动模型，所以对教学设计2进行修改得到教学设计3．经过研讨，她对各种模型的区别有了更深刻的理解．在反思1中也有不少教师谈到研讨对其的影响，如T3：“原来这么多知名人物和‘负负得正’有渊源，‘负负得正’的模型挺多．”T7：“知道了数学知识的起源和发展，数学发展的过程等．”T4：“原来负负得正有着这么多的数学家建立模型去探究，看似简单的结论要经历漫长的历史发展，而不是简单规定出来的．”

5.2.2 教师HCK变化分析

在集中研讨时，分配律模型是不是在证明“负负得正”引发了教师们的激烈争论．经过讨论得知，用分配律模型解释“负负得正”并不属于严格推理证明，因为这种方法是以分配律在负数范围内成立为基础，存在循环论证，这一结果令很多教师震惊．在反思1中教师表达了对此收获的感悟，如T8：“了解了负负得正是无法证明的，知道了很多可以解释的现实模型．”T5：“以史为鉴，原以为用运算律和相反数模型可以严格推理‘负负得正’，没想到是无法证明的，是经现实模型确认的一种约定．”

5.2.3 教师KCS变化分析

了解“负负得正”的历史以及一些名人对这一法则的困惑，可以让教师初步认识到学生在学习这一知识时可能会存在困惑，这一看似简单的规定对学生而言并不简单．在课堂观摩时，基于数学史的探究活动的设计，让学生模仿教师已给的模型解释“负负得正”，学生的回答让教师意识到了学生思维的活跃，以及学生对“负负得正”的认识，改变了教师对学生的认识，如T2在反思2中提到，她在自己学校进行了融入数学史的有理数乘法教学，在向学生讲述司汤达的故事时，学生感到非常震惊，他们从没质疑过“如此简单的问题”，感叹于“原来也有不能证明的数学规定”，学生感受到了数学的魅力，纷纷举手尝试自己解释“负负得正”的合理性，她感受到了学生比她想象中更有能力，更善于思考，自己最大的收获在于，学生敢于像司汤达一样说“我不会”．

5.2.4 教师KCT变化分析

通过阅读史料和集中研讨，教师知道要选择适合学生的模型，更注重算理的解释．如教师T2、T3前后两版教学设计的变化，后一版设计中均采用司汤达的故事引入，用于激发学生学习的兴趣．

再如T8：“研讨最大的收获是知道了如何在课堂中运用数学史料，选取合适的现实模型．”

T5：“研讨很有必要，比如司汤达的故事，只看史料不可能挖掘出很深刻的意义．”

T1：“研讨最大的收获是今后在运算法则课的教学中会更加关注算理的讲解，对于规定的法则会强调其合理性与必要性，而非简单的操练．”

通过对研讨课的观摩和反思，教师普遍认为需要通过探究让学生理解有理数乘法法则的合理性，希望通过有趣的数学故事让学生了解数学是发展的．针对部分学生在自主探究时，不能够清晰描述所列举的模型时，观课教师提出用现实模型解释“负负得正”的关键在于讲清楚“正与负的分界”，如T2：“要讲清楚正负的分界，明确正负的参照点，学生列举的很多模型只涉及到了‘正负’和‘负正’，没有涉及到‘负负’．”T6：“每个模型中0的意义不同，讲清楚模型中0的含义会促进学生对模型的理解．”T1：“在任何模型中，参照点要先设定好，这样正负的区别才会清楚．”

另外，教师在观课反思中谈到了对自己后续教学的启示．如T8：“不再那么理所当然地得出法则，会花一定的时间展示或者探寻法则的合理性，会更重视‘为什么要学’的问题的思考．”T4：“会多给学生思考的时间和空间，让知识的发生更加自然．”T5：“引导学生寻找生活模型前，会和学生一起约定分别表示‘正’和‘负’的量，在学生理解‘负负得正’后，会告诉学生‘负负得正’是一种约定，而不是推理而来．”

5.2.5 教师KCC变化分析

也有教师提到，原来在进行有理数乘法教学时，并不会在法则的解释上花费过多的时间，这一点从前述教师通常在解释法则上所花时间可以佐证，教科书上的运动模型也是一带而过，在了解“负负得正”的历史后，才真正理解了教科书的意图，这属于教师“内容与课程知识”增加，如T8：“了解了历史后，更清楚了模型的归属，理解了教科书的编写安排．”

总体而言，除“一般内容知识”外，从表5可以看出，HPM课例研究对授课教师和观课教师的SCK、HCK、KCS、KCT和KCC均有影响，且无明显差别．结合表3中数据收集的时间节点可以看出，“选题与准备”环节，自主阅读史料进行教学设计主要对教师的SCK和KCT产生影响，教师初步认识了有理数乘法法则的历史和解释模型，并根据自己的理解对教学设计进行了改进，但存在理解不到位的现象，如所发放的历史素材中，有关于“负负得正”无法证明的相关文献，但没有引起教师的重视，教学设计中存在试图用分配律证明“负负得正”的现象．“研讨与设计”环节，主要是对教师的SCK、HCK和KCT产生影响．研讨深化了教师对相关历史和模型的理解，明确了有理数乘法法则和运算律之间的关系．“实施与反馈”环节，研讨课的观摩，教师多倾向于关注数学史料的运用方式对学生的影响，以及学生的课堂表现，所以研讨课的观摩和反思主要对教师的KCS和KCT产生影响．对T8而言，此HPM课例研究还促使其重新理解了教科书的安排，影响了教师的KCC．

6 结论与启示

以HPM视角下“有理数乘法”的课例研究为载体，通过分析HPM工作室8位在职教师课例研究过程中的3版教学设计、2份反思报告和问卷调查，研究者得到如下结论．第一，HPM课例研究不仅可以促进授课教师的专业发展，对参与课例研究的其他在职教师的专业发展均有促进作用，且两者之间无差别，教师的SCK、HCK、KCS和KCT均有改变，个别教师的KCC有所改变．第二，课例研究的4个环节对教师MKT各部分的影响不同：在“选题与准备”环节，主要对教师的SCK和KCT产生影响；在“研讨与设计”环节，主要是对教师的SCK、HCK和KCT产生影响；在“实施与反馈”环节，主要对教师的KCS和KCT产生影响．

另外，研究也证实了研讨是课例研究的核心环节，异质人员参与课例的研讨可以深化拓展教师MKT的改变．在课例研究中，相关史料已在集中研讨前发放给教师，但从教师的教学设计2可以看出教师对数学史料的理解存在偏差，如教师没有理解“负负得正”为什么不能证明．研讨中，高校HPM研究者对史料进行详细的解读，促进了教师对史料的理解和运用，影响了部分教师的SCK、HCK以及KCT的进一步改变．

最后，由于参与课例研究的教师起初对有理数乘法法则和运算律之间的关系缺乏了解，导致教师在研讨中对有理数乘法法则是否可以证明进行了激烈的讨论，教师HCK的变化主要发生在研讨后，所以研究仅针对教师有理数乘法教学所需数学知识的变化进行研究，研究结论不一定适用于其它课题，具有一定的特殊性和局限性．

[1] WOLF J. Lesson study in the United States [R]. 1st Annual Conference on Learning Study. Hong Kong Institute of Education, 2005: 47-66.

[2] 袁丽，胡艺曦．课例研究对促进教师专业发展的作用、不足与改进策略——基于文献的考察[J]．教师教育研究，2018（4）：99-105．

[3] 汪晓勤．HPM的若干研究与展望[J]．中学数学月刊，2012（2）：1-5．

[4] ARCAVI A, ISODA M. Learning to listen: From historical sources to classroom practice [J]. Educational Studies in Mathematics, 2007, 66 (2): 111-129.

[5] FURINGHETTI F. Teacher education through the history of mathematics [J]. Educational Studies in Mathematics, 2007, 66 (2): 131-143.

[6] 蒲淑萍．HPM与数学教师专业发展[D]．上海：华东师范大学，2013：1．

[7] 黄友初．基于数学史课程的职前教师教学知识发展研究[D]．上海：华东师范大学，2014：1．

[8] 彭刚．职前教师数学观发展研究：数学史的视角[D]．上海：华东师范大学，2017：1．

[9] 洪燕君．HPM教学实践驱动下初中数学教师专业发展研究：MKT的视角[D]．上海：华东师范大学，2017：1．

[10] 汪晓勤．HPM与初中数学教师的专业发展——一个上海的案例[J]．数学教育学报，2013，22（1）：18-22．

[11] JANKVIST U T. An implementation of two historical teaching modules: Outcomes and perspectives [C] // History and epistemology in mathematics education-proceedings of the 6th European summer university. Vienna: Holzhausen Publishing, 2011: 139-152.

[12] JANKVIST U T, MOSVOLD R, FAUSKANGER J, et al. Analyzing the use of history of mathematics through MKT [J]. International Journal of Mathematical Education in Science & Technology, 2015, 46 (4): 495-507.

[13] BALL D L. Content knowledge for teaching [J]. Journal of Teacher Education, 2008 (59): 389-407.

[14] CLARK K M. History of mathematics: Illuminating understanding of school mathematics concepts for prospective mathematics teachers [J]. Educational Studies in Mathematics, 2012, 81 (1): 67-84.

[15] FENAROLI G, FURINGHETTI F, SOMAGLIA A. Rethinking mathematical concepts with the lens of the history of mathematics: An experiment with prospective secondary teachers [J]. Science & Education, 2014, 23 (1): 185-203.

[16] MOSVOLD R, JAKOBSEN A, JANKVIST U T. How mathematical knowledge for teaching may profit from the study of history of mathematics [J]. Science & Education, 2014, 23 (1): 47-60.

[17] SMESTAD B. When HPM meets MKT: Exploring the place of history of mathematics in the mathematical knowledge for teaching [C] // BARBIN E, JANKVIST U T, KJELDSEN T H. History and epistemology in mathematics education -proceedings of the 7th European summer university. Copenhagen: Aarhus University, 2015: 539-550.

[18] 巩子坤．调查与分析：“负负得正”何以不易理解[J]．数学教学，2009（8）：7-11．

[19] 巩子坤，张奠宙．数学教学中记忆与理解关系的调查研究[J]．中国教育学刊，2007（9）：71-74．

[20] 汪晓勤．HPM视角下的小学数学教学[J]．小学数学教师，2017（7~8）：77-83．

[21] 佟魏，汪晓勤．负数的历史与“负负得正”的引入[J]．中学数学教学参考，2005（1~2）：126-128．

[22] 斯丹达尔．斯丹达尔自传[M]．周光怡，译．南京：江苏文艺出版社，1998：231-232．

[23] G BOULER. On the esenece of multiplication [J]. For the Learning of Mathematics, 1998, 18 (3): 12-18.

[24] 上海中小学课程教材改革委员会．九年义务教育课本六年级第二学期[M]．上海：上海教育出版社，2006：18-19．

[25] BEMAN W W, SMITH D E. Elements of algebra [M]. Boston: Ginn & Company, 1900: 40-41.

[26] 人民教育出版社课程教材研究所中学数学课程教材研究开发中心．九年义务教育课本七年级下册[M]．北京：人民教育出版社，2006：28-33．

[27] SAUNDERSON N. The elements of algebra [M]. Cambridge: The University Press, 1740: 56-59.

[28] 贾随军，刘明君，叶蓓蓓，等．20世纪以来中学数学教材中“负负得正”法则解释方式的研究[J]．数学教育学报，2015，24（4）：76-81．

[29] EULER L. Elements of algebra [M]. London: Longman, Hurst, Rees, Orme & Co, 1822: 9-11.

[30] 克莱因F．高观点下的初等数学[M]．舒湘芹，译．上海：复旦大学出版社，2008：15-21．

The Influence of HPM Lesson Study on Teachers’ MKT——Taking the Multiplication of Rational Numbers as an Example

LI Xiao-ni, WANG Xiao-qin

(College of Teacher Education, East China Normal University, Shanghai 200062, China)

In lesson study of “multiplication with rational numbers” from the perspective of HPM, we analyzed three editions of instructional design, two kinds of reflection, and questionnaires of eight in-service teachers in the HPM studio and found that HPM lesson study can promote the professional development of participating in-service teachers. Four different steps of the HPM lesson study had different influences on each part of teachers’ mathematical knowledge for teaching (MKT); the results show that discussion was the core step of the of HPM lesson study, and heterogeneous personnel participating in the discussion can deepen the changes in teacher’s MKT.

lesson study; HPM; multiplication of rational numbers

G442

A

1004-9894（2021）03-0083-07

栗小妮，汪晓勤．HPM课例研究对教师MKT的影响[J]．数学教育学报，2021，30（3）：83-89．

2021-03-26

上海高校“立德树人”人文社会科学重点研究基地研究项目——数学课程与教学中落实立德树人根本任务（A8）

栗小妮（1984—），女，山西晋城人，博士生，主要从事数学史与数学教育研究．

[责任编校：陈汉君、陈隽]