克服比例推理的过度使用——抑制控制与工作记忆的视角

李晓东，蔡梦婕，江荣焕

克服比例推理的过度使用——抑制控制与工作记忆的视角

李晓东，蔡梦婕，江荣焕

（深圳大学 心理学院，广东 深圳 518060）

比例推理的过度使用是指学生在解决非比例问题时错误地使用了比例方法的现象．采用负启动范式，以小学四至六年级学生为研究对象，从抑制控制模型及工作记忆容量角度探讨比例推理过度使用的机制．发现：学生在非比例题上要克服比例策略的误导需要抑制控制的参与；工作记忆容量不足时，儿童在解决非比例题时难以克服比例策略的干扰．

比例推理；抑制控制；负启动；工作记忆容量

1 问题提出

比例推理是基于比和比例知识进行推理的一种能力．比是两个数量倍数关系的表达或度量，比例则蕴含了两个变量倍数关系的不变性．比和比例不仅是小学数学的重要内容，更是初、高中学习函数的基础[1]．很多研究发现，当学生掌握了比例推理之后，会出现一种过度使用比例推理的现象，最常见是在加法题上使用比例策略．例如：对于“Sue和Julie跑得一样快，Sue先开始跑，当Julie跑了3圈时，Sue已经跑了9圈，当Julie跑了15圈时，Sue跑了多少圈？”等问题，本应使用加法解决，即15+(9-3)=21，但很多学生都错误地使用了比例方法，即15×(9/3)=45[2-5]．

国内外研究表明，比例推理的过度使用是一种系统性错误．加法是小学低年级学生就已掌握的技能，小学高年级学生以及青少年和成人在加法题上错误地使用比例方法显然不能用概念缺失来解释．抑制控制模型认为认知发展不仅是获得复杂的概念，还必须抑制先前过度学习的知识与技能，青少年及成人在具备了相应的知识与技能后，仍在解决问题时出错，正是抑制控制能力未能充分发挥作用的表现．有学者采用负启动的实验范式发现，被试在解决加法题时，需要抑制比例策略，支持了抑制控制模型[6]．

采用负启动范式作为抑制控制的测量方法，其基本原理是如果在前一个试次（trial）中要抑制一个刺激或策略，在下一个试次却要激活该刺激或策略时，需要付出执行代价，表现为反应时的延长或错误率的上升[7，8]．根据负启动的定义，负启动效应只有在被试在启动项上做出正确反应时才能观测到．这使得一些研究的被试剔除率较高，例如，在Lubin等人和江荣焕等人的研究中，六年级学生在文字应用题上的剔除率分别为28%和43%[6，9]．但目前没有研究关注这些学生在启动问题上失败的原因，即为什么这些学生没能克服这些过度学习策略的误导．

工作记忆容量的执行注意理论认为，抑制是一个需要资源的过程，个体在工作记忆容量上的差异代表控制注意的差异，后者导致了抑制能力的个体差异[10]．关于工作记忆个体差异的研究表明，高工作记忆容量的个体其注意执行功能更强，能更有效地对抗干扰[11]．Diamond认为抑制控制和工作记忆共享一个有限的认知容量资源，工作记忆系统对抑制控制系统具有支持作用，个体必须牢记并明确目标才能有效地抑制干扰[12]．工作记忆是执行功能最为基础的成分，其发展反映了包括抑制控制的其它执行功能的发展，成功的抑制控制是好的工作记忆的结果．许多研究表明工作记忆容量与学生数学表现有关[11-14]．也有研究表明工作记忆容量小的学生更倾向于依靠直觉策略而不是基于规则的算法策略[15]．还有研究通过施加时间压力或增加工作记忆负荷，诱发了被试更严重的过度使用比例策略的倾向[16]．这些研究都表明工作记忆容量可能限制了抑制功能的发挥从而影响学生数学问题解决的效果．但尚未见到对成功解题组与未成功解题组在工作记忆容量上是否有显著差异的实证研究发表．

综上，研究拟从抑制控制模型及工作记忆容量角度探讨比例推理过度使用的机制，并假设克服比例推理的过度使用需要抑制控制的参与，个体在非比例题上未能抑制比例策略的误导与其工作记忆容量较小有关．

抑制控制模型认为个体抑制控制的效率会随着年龄增长而提高[7，17]．但之前关于数学问题解决的研究并不支持这一观点，研究发现六、八年级和大学生的抑制控制效率并没有显著差异[6，9]．推测这可能是由于成功解决启动问题的儿童，其抑制控制能力已达到较为成熟的水平，因此他们的抑制控制效率与青少年和成人没有发展性差异．抑制控制效率的发展性差异可能在更小年龄的儿童中表现出来，为检验这种可能性，研究选取小学四～六年级学生作为被试．

2 研究方法

研究主要解决3个问题．第一，考查抑制控制在克服比例推理过度使用中的作用．如果被试成功解决非比例问题（即克服了比例推理过度使用）需要抑制控制的参与，则会出现负启动效应．第二，探讨没有克服比例推理过度使用的原因是否是因为学生工作记忆容量不足，导致其无法抑制比例策略的误导．对比在非比例问题上成功组与失败组在数字工作记忆和空间工作记忆广度上是否有差异．第三，考查小学生的抑制控制效率是否随着年龄增长而增长，指标为负启动量．

2.1 被试

被试来自南方某市3所普通公立小学．随机抽取四年级学生61人（男40人，女21人，平均年龄10.06±0.74岁），五年级学生60人（男31人，女29人，平均年龄10.79±0.65岁），六年级学生54人（男20人，女34人，平均年龄11.74±0.72岁）．实验之前先通过班主任等老师了解学生的信息，排除智力有缺陷或存在阅读障碍的被试．所有被试的视力或矫正视力正常，无红绿色盲，均未参加过类似实验．

2.2 实验材料与程序

2.2.1 抑制控制能力的测量

研究中抑制控制能力是指在解决加法题时抑制比例策略的能力．共设计了3类文字应用题：比例题，加法题和中立题，样例见表1．采用负启动实验范式，在测试试次中，启动项为加法题，探测项为比例题；在控制试次中，启动项为中立题，探测项为比例题，要求对答案进行对错判断，实验流程见图1．实验的逻辑是如果被试在启动阶段解决加法题时需要抑制比例策略，那么在探测阶段解决比例问题时，被试就需要付出额外的“代价”来激活比例策略，从而出现负启动效应．同控制试次相比，被试在测试条件下在探测项上的反应时或错误率会增加．

表1 3种题型示例（划线处为错误答案）

被试进行6个试次的练习，比例题、加法题、中立题各两道，每类题目答案正误各1道．练习过程中屏幕上会自动给出反馈，如果被试出现太多错误，可以再练习一次．为了平衡练习可能带来的启动效应，练习中的题目均为随机呈现，且不会在正式实验中出现．练习结束后，被试将完成16个实验试次，控制试次和测验试次各8个，比例题16道、加法题和中立题各8道．为平衡实验条件间的顺序效应及可能出现的习惯化反应，16个试次的呈现顺序采用伪随机设计，同种类型的试次不会连续出现3次或以上，测试试次与控制试次中的题目则是完全随机出现．实验流程见图１．

2.2.2 数字工作记忆广度任务

要求被试完成随机的两个一位数的加减心算（答案为一位正数）并记住答案，最后按顺序回忆答案．实验任务从一道算术题开始，被试运算并回忆正确后进行下一组任务．每一组任务都比上一组多一道算数题，以此类推，共10组任务．当出现运算或回忆错误时，重复此组任务但题目不重复，直至连续两次回忆错误则终止实验．被试能够达到的正确回忆的最高水平记为被试的数字工作记忆广度[18]．

2.2.3 空间工作记忆广度任务

采用Corsi积木点任务设计的计算机程序[19]，用25个黑边白底的小方块（2cm×2cm）代替积木，按5×5矩阵形式在计算机屏幕中央白色背景中（36cm×27cm）呈现．实验中会从25个方块中随机产生1个方块变成黑色，停留800毫秒后变回原来的白色，接着随机产生另一个白色方块变黑．被试的任务是记住方块变化的顺序并在作答页面用鼠标按先后顺序点击颜色变化过的方块．正式实验从3个随机分布的方块开始，逐渐往上递增，直至9个随机分布的方块．每个广度呈现3组，被试正确回忆两组及以上则认为达到这一广度要求，可进行下一广度的任务．当被试在某一水平的3次测试中，答错两次则退出测试．被试能够正确按顺序点击的方块的个数记为该被试的空间工作记忆广度．

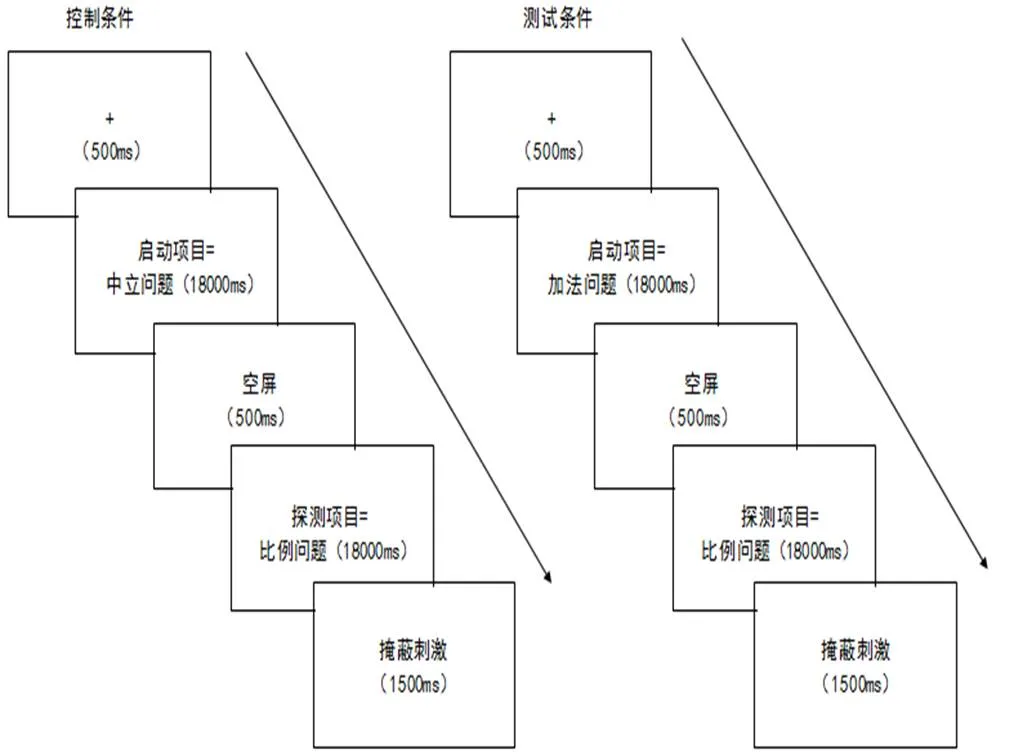
图1 实验刺激呈现流程

2.3 实验设计

采用2（实验条件：测试vs.控制）× 2（组别：成功vs.失败）×3（年级：四～六年级）的混合实验设计，实验条件为被试内变量．因变量为被试在两种实验条件下在探测项（比例题）上的反应时和错误率，数字工作记忆广度和空间工作记忆广度．

2.4 实验流程

在多媒体教室中进行集体施测．所有任务都在计算机上完成，采用E-prime2.0编写程序，数据管理采用SPSS22.0分析．首先完成负启动实验任务，其次是数字工作记忆任务和空间工作记忆任务．每种任务之间都安排了休息时间．

3 实验结果

剔除缺失数据和反应处于随机水平以及中立题与比例题上错误率高于50%的被试，共121名被试进入最终分析．

3.1 抑制控制在克服比例推理过度使用中的作用

根据负启动的实验逻辑，负启动效应只能在被试正确解决加法题的前提下出现，因此将正确率低于或等于50%的被试予以剔除（这部分被试称为失败组），包括21名四年级学生、21名五年级学生、17名六年级学生．进入负启动分析的被试共有62名学生（这部分学生称为成功组），包括12名四年级学生、23名五年级学生、27名六年级学生．将错误反应的反应时剔除，同时剔除各类题目的平均反应时±3个标准差之外的数据．被试在探测项目上平均反应时和错误率见表2．以被试在探测项目上的反应时和错误率为因变量，进行2（实验条件：控制vs.测试）×3（年级：四～六年级）的重复测量方差分析．

对探测项目错误率的方差分析表明，实验条件的主效应不显著（(1, 59)=0.434，>0.1）；年级主效应不显著（(2, 59)=0.273，>0.1）．年级与实验条件的交互作用显著（(2, 59)=3.489，<0.05，2=0.106）．简单效应分析发现除五年级在实验条件上差异边缘显著外（测试-控制=26.63-20.11= 6.52，=0.062），其它均无显著差异．说明实验条件与年级对学生的解题成绩没有显著影响．

对探测项目反应时的方差分析表明，实验条件主效应显著（(1, 59)=5.010，<0.05，2=0.078），被试在测试条件下解答比例题所需要的时间（7 837.75±2 615.75ms）显著长于控制条件下所需要的时间（7 350.89±2 547.62ms），出现了负启动效应．此外，年级主效应不显著（(2, 59)=0.060，>0.1），年级与实验条件的交互作用不显著（(2, 59)=0.962，>0.1）．说明小学四～六年级学生在解决加法题上要克服比例策略的误导，需要抑制控制的参与，但各年级学生的抑制控制效率没有显著差异．

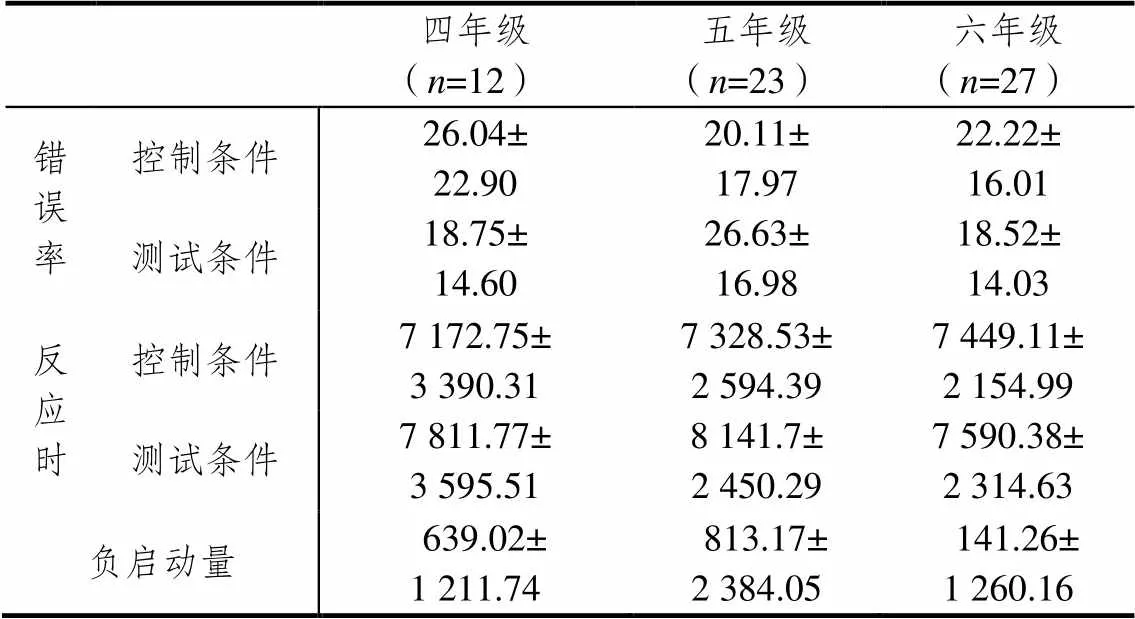
表2 各年级被试在探测项目上的错误率和反应时（M±SD）

注：负启动量=测试试次中探测项目的反应时-控制试次中探测项目的反应时

3.2 工作记忆容量在克服比例推理过度使用中的作用

成功组与失败组学生的工作记忆容量的平均数和标准差见表3．2（组别：成功vs.失败）×3（年级：四～六年级）的方差分析表明，在数字工作记忆广度上，组别主效应显著（(1, 115)=5.932，<0.05，2=0.049），成功组的工作记忆容量大于失败组．年级主效应显著（(2, 115)=4.815，<0.05,2=0.077），事后比较发现，四年级和六年级在数字工作记忆广度上差异显著（六-四=6.52-5.61=0.91，<0.01）；五年级和六年级在数字工作记忆广度上差异显著（六-五=3.52-5.95=0.57，<0.05），四年级和五年级在数字工作记忆广度上不显著．年级与组别的交互作用不显著．在空间工作记忆广度上，组别主效应显著（(1, 115)=4.080，<0.05，2=0.034），成功组的工作记忆广度大于失败组．年级主效应、年级与组别的交互作用均不显著．

为了探究工作记忆容量与学生解决加法题成绩之间的关系，进一步做了相关分析，结果见表4，从表4中可见学生在加法题上的错误率与数字工作记忆广度呈显著的负相关，与空间工作记忆广度无显著关系．为了考查工作记忆广度对解题成绩的预测作用，采用enter方法、将年级转化为虚拟变量做了回归分析．结果发现，只有数字工作记忆广度可以显著预测学生在加法题上错误率（=-0.23，<0.05）可以解释12%的变异数．

表3 成功组与失败组工作记忆容量（M±SD）

表4 非比例题错误率与工作记忆的相关分析（M±SD）

注：*表示<0.05，**表示<0.01

3.3 成功组与失败组解题能力的比较

为排除成功组与失败组在解题能力上有差异，比较了控制试次中，两组被试在中立题和比例题上的错误率和反应时，结果见表5．

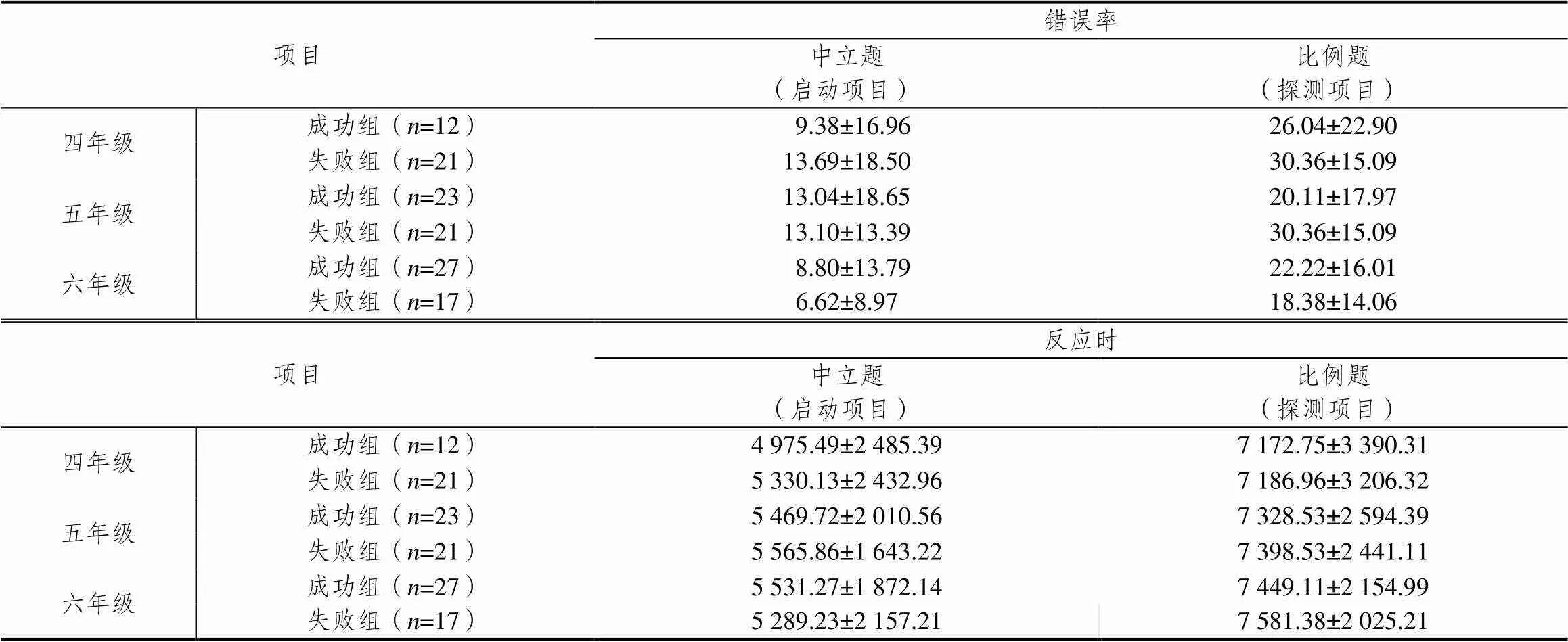
表5 各年级被试在控制试次上的错误率和反应时（M±SD）

方差分析表明，组别主效应均不显著（错误率：中立(1, 115)=0.063，=0.80、比例(1, 115)=1.308，=0.26；反应时：中立(1, 115)=0.032，P=0.86、比例(1, 115)=0.022，=0.883）；年级主效应不显著（错误率：中立(2, 115)=1.342，=0.27、比例(2, 115)=2.113，=0.13；反应时：中立(2, 115)=0.284，=0.75、比例(2, 115)=0.145，=0.87），二者的交互作用也不显著（错误率：中立(2, 115)=0.393，=0.68、比例(2, 115)=1.928，=0.15；反应时：中立(2, 115)=0.188，=0.83、比例(2, 115)=0.005，=1.00）．表明成功组与失败组在解决中立题和比例题的能力上不存在差异．

4 讨论

抑制控制在数学学习中的作用日益受到重视[20]．研究从抑制控制模型出发，探讨抑制控制在小学生克服比例推理过度使用中的作用，以及小学四～六年级学生在抑制控制的效率上是否具有发展性差异，并通过比较在加法题上成功组与失败组被试的工作记忆容量，探讨工作记忆在克服比例推理的过度使用中的作用．

研究发现：小学生在正确解决加法题后再解决比例题时，反应时明显变长，出现了负启动效应，说明他们在先前加法题上抑制比例策略、之后在比例题上又重新激活该策略时需要付出执行代价．这一结果说明，儿童在解决加法题时，不仅需要掌握加法的相关概念与运算法则，而且需要抑制误导策略的干扰，这一结果与江荣焕等人的一致[6]．儿童在生活中会遇到很多与比例题有关的情境，如浓度问题、时间速度路程问题，使得他们对比例题较为熟悉．在数学学习的过程中，比例题又常以缺值形式呈现，即在问题中，依次给出、、，要求求出第4个数，使得=，或=[2]，导致学生容易根据经验和题目呈现的形式形成一种不证自明的直觉反应[21]，即启发式策略．当遇到与比例策略冲突的缺值形式的加法题时，启发式系统与分析式系统就会产生竞争，学生必须启动抑制控制机制来阻止比例推理这种启发式策略的误导，方能正确解决问题．

研究也发现：尽管被试是小学生，但在抑制控制效率上仍未观察到发展性差异，这一点与抑制控制模型的假设不一致，但与其它关于文字应用题的研究一致[6，9]．这可能与负启动范式的严格标准有关，根据负启动范式的要求，只有在启动问题上正确的被试，才能进入下一步的分析．能够成功抑制比例策略干扰的小学生，其抑制控制能力水平是相当高的．那么，那些没有进入分析的被试会不会是因为数学能力较差，而不是无法抑制误导策略呢？研究者比较了成功组和失败组被试在中立题和比例题上的成绩，发现两者没有显著差异，说明他们至少在比例推理的能力上是没有差异的．从数学知识体系上讲，加法表达的是绝对量，比例表达的是相对量，加法在一二年级就已经掌握，而比例要在高年级才学习．因此，可以推断两组被试在复杂数学能力上没差异时，其简单数学技能也应没有差异．失败组被试并不是因为加法知识掌握得不好，而是在解决加法题时无法抑制比例策略的误导造成的．

那么失败组为什么无法抑制误导策略的干扰呢？研究者首次对这个问题进行了研究．认为与其工作记忆容量较小有关．双加工理论认为存在两种不同的加工系统，系统1是直觉/启发式的，其特点是快速、自动化，基于联想且无需努力，不占用工作记忆容量；系统2是缓慢、分析式的，需要努力且占用工作记忆容量[22]．一般来说，儿童和成人都会优先使用系统1，但系统1并不总是导致正确答案，此时就需要系统2来抑制系统1的错误反应[7]．研究发现成功组无论是数字工作记忆广度还是空间工作记忆广度均大于失败组，这使得他们在加法策略与比例策略出现竞争时，有足够的资源去抑制比例策略的误导；而失败组的被试则因为其较小的工作记忆广度而无力抑制干扰，从而依赖于不占用工作记忆容量的启发式策略，导致了错误答案．对于两种工作记忆的作用，回归分析表明，对于解决加法题，数字工作记忆广度的作用更大，这可能是因为研究的任务不涉及空间概念．在数字工作记忆广度方面四年级明显低于五、六年级学生，但空间工作记忆广度上无年级差异．四年级成功解决非比例题的人数较少，可能与其数字工作记忆广度小有关．值得注意的是，研究中的失败组学生并不是数学学困生，他们的数学能力与成功组是相当的，他们之所以在加法题中表现不佳，可能是因为其工作记忆容量较小而无法抑制比例策略的误导造成的．工作记忆的个体差异值得重视，特别是在数学问题解决的过程中，学生既需要对题目的文字进行加工和记忆，同时还需要抑制先前过度学习的知识的误导，这可能是导致学生数学问题解决不佳的一个重要原因．另外，研究中被试剔除率较高，说明文字应用题对小学生来说认知负荷较高，未来研究可考虑降低任务难度[23-30]．

研究表明：学生虽然已经早已掌握了加法知识，但依然在相关问题上犯了过度使用比例推理的错误，说明学生在数学问题解决过程中仅有知识或算术技能是不够的．在面对问题时，会有多种策略在头脑中竞争，此时必须抑制误导性策略才能正确解决问题．因此在数学教育中，应该加强学生抑制控制能力的培养．为让学生更好地意识到不同策略的不同作用，在教学中教师应有意识地将可能引起学生误解的题目呈现给学生，培养学生分析问题的能力．同时，工作记忆容量大小是影响抑制功能发挥的关键因素，因此可以尝试对学生进行工作记忆训练．

5 结论

小学四～六年级学生在解决非比例题时要克服比例策略的误导需要抑制控制的参与，抑制控制效率未见发展性差异．工作记忆容量影响抑制控制功能的发挥．

[1] 史宁中，娜仁格日乐．小学数学教科书中的比及其教学[J]．数学教育学报，2017，26（2）：1-5．

[2] 李晓东，江荣焕，钱玉娟．中小学生对比例推理的过度使用[J]．数学教育学报，2014，23（6）：73-77．

[3] Jiang R, Li X, Fernández C, et al. Students’ performance on missing-value word problems: A cross-national developmental study [J]. European Journal of Psychology of Education, 2017, 32 (4): 1-20.

[4] Van Dooren W, De Bock D, Evers M, et al. Students’ over-use of proportionality on missing-value problems: How numbers may change solutions [J]. Journal for Research in Mathematics Education, 2009, 40 (2): 187-211.

[5] Fernández C, Llinares S, Dooren W V, et al. The development of students’ use of additive and proportional methods along primary and secondary school [J]. European Journal of Psychology of Education, 2012, 27 (3): 421-438.

[6] 江荣焕，李晓东．比例推理的过度使用及其认知机制：一项发展性的负启动研究[J]．心理学报，2017，49（6）：745-758．

[7] Houdé O, Borst G. Measuring inhibitory control in children and adults: Brain imaging and mental chronometry [J]. Frontiers in Psychology, 2014, 5 (7): 616.

[8] Tipper S P. Does negative priming reflect inhibitory mechanisms? A review and integration of conflicting view [J]. Quarterly Journal of Experimental Psychology A Human Experimental Psychology, 2001, 54 (2): 321-343.

[9] Lubin A, Vidal J, LanoëC, et al. Inhibitory control is needed for the resolution of arithmetic word problems: A developmental negative priming study [J]. Journal of Educational Psychology, 2013, 105 (3): 701-708.

[10] Redick T S, Heitz R P, Engle R W. Working memory capacity and inhibition: Cognitive and social consequences [M] // Gorfein D S, Macleord C M. Inhibition in Cognition. American Psychological Association, 2007: 125-142.

[11] 蔡丹，李其维，邓赐平．工作记忆新探：基于个体差异的研究[J]．心理发展与教育，2010，26（2）：205-209．

[12] Diamond A. Executive functions [J]. Annual Review of Psychology, 2012, 64 (1): 135-168.

[13] 王恩国．工作记忆与学习能力的关系[J]．中国特殊教育，2007（3）：78-84．

[14] 李晓东，聂尤彦，庞爱莲，等．工作记忆对小学三年级学生解决比较问题的影响[J]．心理发展与教育，2003，19（3）：41-45．

[15] Beilock S L, Decaro M S. From poor performance to success under stress: Working memory, strategy selection, and mathematical problem solving under pressure [J]. J Exp Psychol Learn Mem Cogn, 2007, 33 (6): 983-998.

[16] Gillard E, Dooren W V, Schaeken W, et al. Dual processes in the psychology of mathematics education and cognitive psychology [J]. Human Development, 2009, 52 (2): 95-108.

[17] HoudéO, Pineau A, Leroux G, et al. Functional magnetic resonance imaging study of piaget’s conservation-of-

number task in preschool and school-age children: A neo-piagetian approach [J]. Journal of Experimental Child Psychology, 2011, 110 (3): 332-346.

[18] 李德明，刘昌，李贵芸．数字工作记忆广度的毕生发展及其作用因素[J]．心理学报，2003，35（1）：63-68．

[19] 刘昌．数学学习困难儿童的认知加工机制研究[J]．南京师范大学学报（社会科学版），2004（3）：81-88．

[20] Star J R, Pollack C. Inhibitory control and mathematics learning: Definitional and operational considerations [J]. ZDM, 2015, 47 (5): 1-5.

[21] Bock D D, Dooren W V, Verschaffel L. Students’ overuse of linearity: An exploration in physics [J]. Research in Science Education, 2011, 41 (3): 389-412.

[22] Evans J S, Stanovich K E. Dual-process theories of higher cognition: Advancing the debate [J]. Perspectives on Psychological Science, 2013, 8 (3): 223-241.

[23] 章全武．改革开放四十年小学数学统计与概率内容嬗变研究——基于七份课程文件的内容分析[J]．数学教育学报，2020，29（6）：69-73．

[24] 岳增成，沈中宇，王鑫，等．影响小学数学教师HPM实践的叙事研究[J]．数学教育学报，2020，29（6）：74-79．

[25] 朱立明，马云鹏．小学数学中“除法”“分数”与“比”的辨析与思考[J]．数学教育学报，2020，29（5）：32-35．

[26] 杨健，李磊，傅海伦．中国当代小学数学课程目标发展演变的特征分析[J]．数学教育学报，2020，29（5）：36-40．

[27] 陶红强．小学生数学符号意识分析框架的构建[J]．数学教育学报，2020，29（5）：41-45．

[28] 尹瑶芳．小学数学教师图形与几何知识状况调查——以上海市浦东新区为例[J]．数学教育学报，2020，29（5）：46-51．

[29] 刘喆，苏新冰，杜炫杰．智慧教室环境下的数学课堂教学行为研究[J]．数学教育学报，2020，29（4）：44-51．

[30] 邓海英，魏亚楠，严卿．小学四年级学生数学情境问题解决能力调查研究——以湖南省为例[J]．数学教育学报，2020，29（4）：52-57．

Overcoming the Overuse in Proportional Reasoning——The Role of Inhibitory Control and Working Memory

LI Xiao-dong, CAI Meng-jie, JIANG Rong-huan

(School of Psychology, Shenzhen University, Guangdong Shenzhen 518060, China)

Overuse of proportional reasoning refers to students improperly using proportional methods in solving non-proportional problems. The present study explored the cognitive mechanism of this phenomenon using the negative priming paradigm based on the Inhibitory Control Model and Working Memory Capacity theory. A total of 175 primary school students (61 fourth graders, 60 fifth graders, and 54 sixth graders) participated in this experiment. The results showed that negative priming effects were significant for all three age groups, and inhibitory control was needed to overcome the use of proportional methods in solving non-proportional problems. Students who failed in non-proportional problems had lower working memory capacity than students who succeeded in non-proportional problems. Digit working memory span could significantly predict the error rates of non-proportional problems. The result showed that it was hard to overcome the inhibition of proportional methods for children who had lower working memory capacity when solving non-proportional problems.

proportional reasoning; inhibitory control; negative priming; working memory

G442

A

1004–9894（2021）03–0073–05

李晓东，蔡梦婕，江荣焕．克服比例推理的过度使用——抑制控制与工作记忆的视角[J]．数学教育学报，2021，30（3）：73-77．

2021–02–25

国家社会科学基金教育学一般项目——认知抑制与数学问题解决的实验研究（BBA170062）

李晓东（1965—），女，辽宁沈阳人，教授，博士，主要从事认知发展与学习、数学问题解决研究．

[责任编校：陈隽、陈汉君]