WPI⁃PAs胶粒在NaCl作用下的团聚动力学及团聚体分形结构

谢彩凤，何志成,伍春娴，蒋赣，魏丹

（广东药科大学医药化工学院/广东省化妆品工程技术中心，广东中山 528458）

乳清分离蛋白（Whey Protein Isolate，WPI）不仅具有极高的营养价值和生物活性，而且具有良好的凝胶特性，常被用于食品、医药等领域[1-2]，WPI的凝胶受离子浓度、电解质类型、温度、pH等因素的影响[3-4]。前期，本课题组以CaCl2做电解质，研究了WPI常温下在慢速团聚（reaction limited aggrega‐tion，RLCA）条件下的团聚动力学和团聚体结构[5]。本研究选用另一种含有单价阳离子Na+的电解质，用广角光散射仪的动态光散射（dynamic light scat‐tering，DLS）方法和小角光散射仪的静态光散射（Static Light Scattering，SLS）方法，研究不同电解质类型对WPI的团聚动力学和团聚体结构的影响，拟为蛋白质的分析检测以及蛋白质团聚体在多孔材料和药物缓释领域的应用提供方法指导。

1 仪器与试剂

1.1 仪器

针头式过滤器（25 mm GD/X，滤纸孔径0.45μm，英国Whatman公司）；广角光散射仪、BI-200SM角度测量器（美国Brookhaven Instruments）配以Ventus LP532型激光发射器（英国Laser Quantum），入射光波长为λ1=532 nm，测角范围20～145°；Mastersizer 2000小角光散射仪（英国Malvern），入射光波长为λ2=633 nm，测角范围0.02～40°。

1.2 试剂

WPI粉末（BiPro，JE345-3-420，Davisco Foods International Inc.，美国明尼苏达）；叠氮化钠（NaN3）、NaOH（固体）、盐酸溶液（0.1 mol/L）、4-羟乙基哌嗪乙磺酸缓冲溶液（HEPES）、NaCl（固态）均为分析纯，由Sigma-Aldrich公司提供；超纯水（自制）。

2 方法

2.1 WPI的热变性制备WPI-PAs及性能测量

WPI热变性制备乳清分离蛋白初级团聚体（WPI-PAs）的方法参见前期的工作[5]，最终得到Cp=50 g/L的胶体分散体，NaN3的最终浓度为3.08×10−3mol/L。配置好的分散体储存于温度为4℃左右的冰箱中备用。

2.2 用NaCl诱导团聚实验及分析检测

实验开始前，先用超纯水对WPI-PAs胶体分散体和NaCl溶液进行多次稀释，以免胶体溶液和电解质溶液浓度太高导致团聚实验过程中局部混合不均而出现大团聚体。然后把稀释的NaCl溶液倒入胶体分散体中达到设定的电解质浓度Cs（mol/L）、胶粒浓度（固定Cp=2.00 g/L）和设定的pH7.0。平衡几秒后，将溶液分成两等份，分别装入2只WALS专用测试瓶，一瓶置于WALS测试槽（恒温25℃）进行DLS测量，测量团聚体的平均水力学半径〈Rh〉与时间的关系；另一瓶置于与测试槽温度相同的恒温水槽中保持恒温，非常缓慢地轻轻来回颠倒，每20～30 min两瓶交换一次测量，以避免生成的大团聚体在长时间静止状态下沉淀到反应器底部。〈Rh〉通过Stockes-Einstein方程计算[6]：

SLS测试的制样方法同DLS，测试时用注射器迅速但轻轻地把团聚体系注入SALS测试槽，在线检测胶粒的团聚动力学过程。SLS所测得的团聚体的光散射强度I(q)的表达式如下[6-7]：

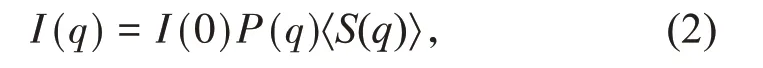
式中：q是基于散射角θ计算得到的波矢量；I(0)是q=0的散射强度；P(q)是初级团聚体WPI-PAs的形状因子，由直接测量浓度为2.00 g/L的WPI-PAs分散体得到；〈S(q)〉是电解质诱导团聚得到的团聚体的归一化形状因子，对初级团聚体可以认为〈S(q)〉=1；q是基于散射角θ计算得到的波矢量：

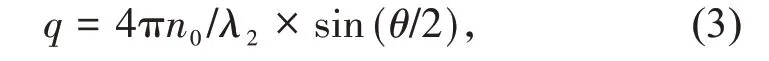
式中：n0是分散介质水的折光指数。

团聚体的平均旋转半径〈Rg〉*和分形维数Df，可以从〈S(q)〉得到[6,8]:

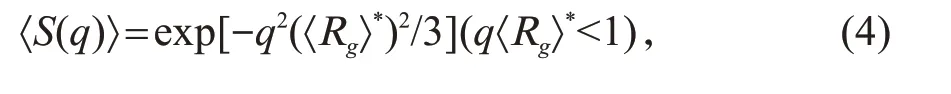
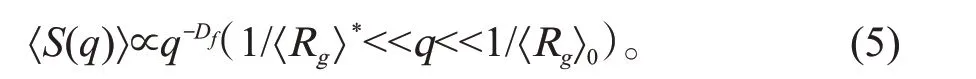
由方程（4）和（5）所得到的平均旋转半径只有在团聚体足够大时才正确，对小团聚体，如在团聚过程初始阶段生成的团聚体，初级团聚体对旋转半径的贡献需要考虑进来：

式中：Rg,0的测试方法见文献，测量值为70.54 nm。

3 结果与讨论

3.1 广角光散射仪的DLS测试结果

图1是用DLS测得的WPI-PAs在不同Cs下各体系的平均水力学半径〈Rh〉随时间的变化规律。从图1可见，不同Cs下，〈Rh〉均随时间的增加而增长，〈Rh〉是直接与粒子的几何形状有关的尺寸，〈Rh〉增大表明WPI-PAs发生了团聚，NaCl的加入对体系的稳定性起着一定的破坏作用。同时可以发现，当Cs为3.20 mol/L时，曲线增长非常缓慢，随着Cs增大，曲线逐渐变得陡峭，〈Rh〉的增长速度逐渐加大，Cs=5.10 mol/L时，曲线最陡，表明此时的团聚速度最快，这是因为电解质中的阳离子Na+屏蔽了蛋白质表面阴离子形成的双电层，Na+浓度越大，双电层被屏蔽的越多，团聚速度更快。

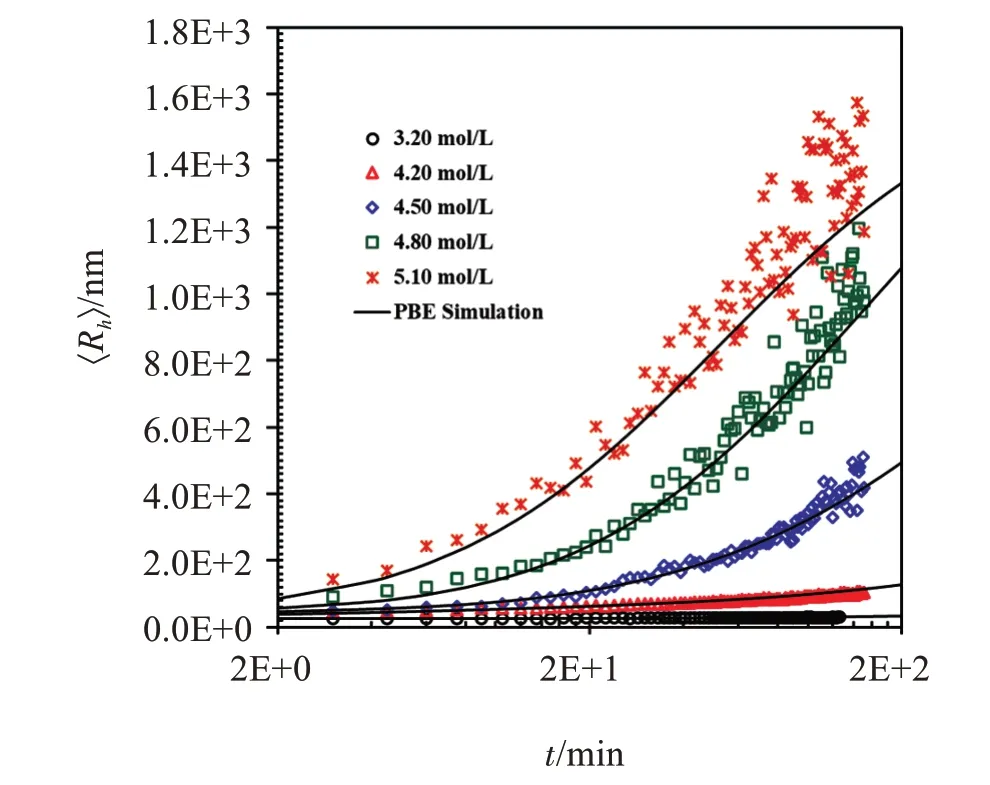
图1 不同NaCl浓度下WPI-PAs团聚体平均水力学半径（〈Rh〉）随时间（t）的变化趋势Figure 1 The hydrodynamic radius,〈Rh〉,as a function of time,t,at the same WPI-PAs concentration but different NaCl concentrations

为了进一步研究WPI-PAs的团聚规律和团聚体结构，引入质量守恒方程（PBE，population balance equation）拟合〈Rh〉-t曲线，胶粒团聚过程中团聚体质量分布可以用PBE模型表述[6,9-11]：

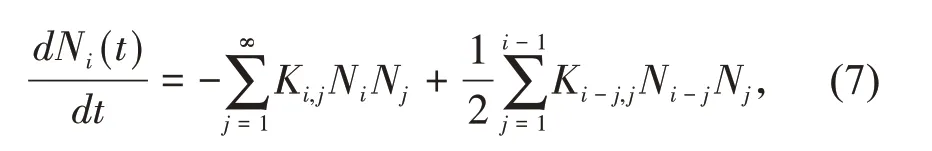
式中：Ni(t)是质量为i的团聚体在时间t的质量浓度；Ki,j是质量为i和j的2个团聚体之间的团聚速率常数，定义如下：

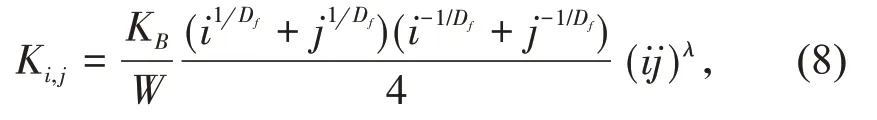
式中：KB=8kT/3μ是Smoluchoeski速率常数（k是波尔兹曼常数，单位是J/K，T和μ分别是分散体的温度和动力学黏度，单位分别为K和Pa·s）；W是Fuchs稳定性常数，典型DLCA团聚过程其值小于5，而对RLCA团聚其值大于5，W值越大表明团聚速度越慢；乘积项(ij)λ表示在RLCA团聚过程中，团聚体的反应速率随团聚体质量的增加而增大，指数λ值的范围一般是0～0.50，DLCA团聚的λ=0。公式(7)和(8)的解能给出整个团聚过程中不断长大的所有团聚体的质量分布（Ni，i=1,2，……），从Ni就可以计算出团聚体的平均水力学半径〈Rh〉和旋转半径〈Rg〉的值：

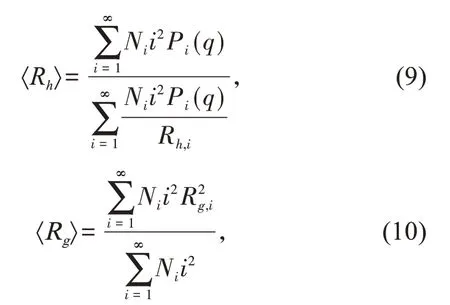
式中：Rh,i和Rg,i是质量为i的单个团聚体的水力学半径和旋转半径，典型的无融合胶体在DLCA和RLCA条件下Df值分别在1.75和2.10左右，很多研究结果都证明了这个结论[6,8]。图1中的连续曲线是用上述方法得到的各浓度下〈Rh〉的拟合结果，相应的拟合参数见表1。可见，各个浓度下的拟合曲线都能较好地与实验值吻合；W值随Cs的增加而减小，说明随团聚速度随电解质浓度增加而加快，因为电解质浓度越大，对双电层的屏蔽也越有效。得到的Df、W和λ的值均与典型的RLCA条件下不融合胶粒的经验值相符合，说明在NaCl作用下WPIPAs的所有团聚均在慢速团聚条件下进行，即使在接近常温NaCl饱和浓度（NaCl常温下的饱和浓度为6.02 mol/L，由于实验时需要将配制的NaCl溶液与胶体分散体混合稀释，所以团聚体系最终能达到的NaCl为5.10 mol/L）时W值仍然很大，是速度较慢的慢速团聚。这与前期用CaCl2诱导团聚在较低浓度出现临界聚沉值[5]（ccc，critical coagulation con‐centration）的现象不同，这是因为CaCl2溶液中含有二价阳离子Ca2+，其他条件都相同时，ccc值与反离子价态的6次方成反比，Ca2+比Na+能更加有效地屏蔽双电层[12]：

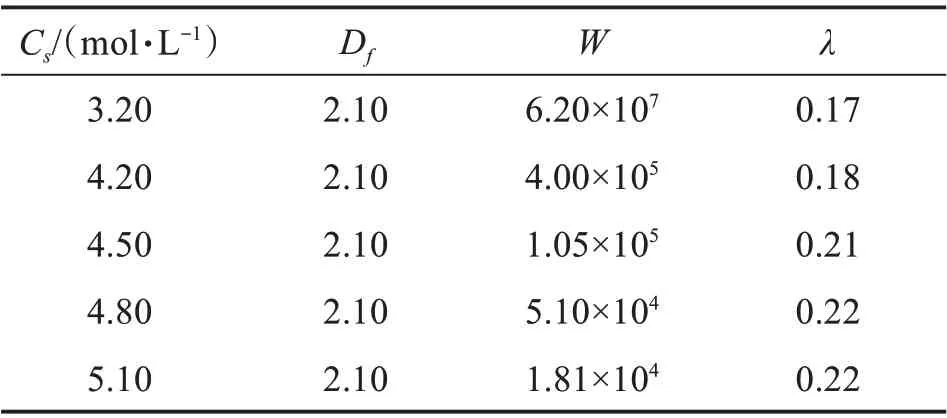
表1 不同NaCl浓度下用PBE方程对WPI-PAs的〈Rh〉-t曲线拟合得到的拟合参数Table 1 The fitting parameter from the PBE simulations of〈Rh〉-t curve of WPI-PAs under different NaCl concentra‐tions

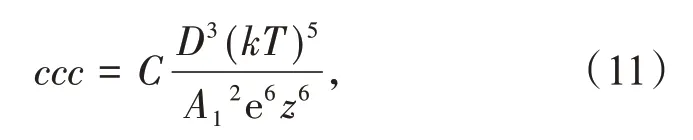
式中：C是与电解质的阴离子和阳离子性质有关的常数；D是介质的介电常数；T为绝对温度（K）；A1是范德华引力常数；e是单位电荷。

用2种电解质得到的团聚体在RLCA条件下Df值均为2.10左右，说明用2种电解质得到的团聚体的结构是相似的。分形体一个非常有趣的性质就是自相似性，即同一物质的分形体在不同尺寸时的形状是非常相似的[13]。正是因为这种自相似性，可以用分形维数Df表征分形体的结构，它代表了分形体中组成成分的紧密程度，Df的值越大说明所得到的团聚体的结构越致密。同一种物质即使采用两种不同的电解质诱导团聚，在相同的团聚机理下得到的团聚体的形状也是相似的，这更进一步证明了拟合结果的可靠性。由于用CaCl2诱导团聚会出现ccc，当CaCl2的浓度高于ccc时，团聚会在DLCA下进行，这时形成的团聚体的Df值一般在1.75左右，说明形成了疏松的团聚体[5]，而本文中在所有NaCl浓度下得到的都是结构致密的团聚体。

3.2 小角光散射仪的SLS测试结果

为了进一步验证实验结果的可靠性，选择Cs=4.50 mol/L的浓度再次诱导团聚并且用小角光散射仪的SLS对团聚过程进行测试。图2（a）和（b）分别是WPI-PAs团聚体的光散射强度I(q)曲线随时间的演化曲线和相应的不同时间的团聚体的归一化平均结构因子〈S(q)〉与归一化的波矢量q×〈Rg〉的函数关系图。图2（a）中，在q<2×10−4处不同时间的曲线几乎重叠，但在q>2×10−4处，I(q)曲线随着团聚过程的进行逐渐上扬，I(q)的值随团聚过程的进行显著增大，这表明团聚体随着凝胶过程的进行逐渐长大，这种缓慢、渐进的团聚体增长表明WPI-PAs的团聚是在RLCA下进行的。对具有分形结构的团聚体，如果团聚体结构相同，不同时间的团聚体归一化的平均结构因子〈S(q)〉−q×〈Rg〉曲线将会重叠在一起，而本文得到的图2（b）中不同时间的〈S(q)〉−q×〈Rg〉曲线确实重叠在一起，说明团聚过程中的团聚体符合分形结构的规律。

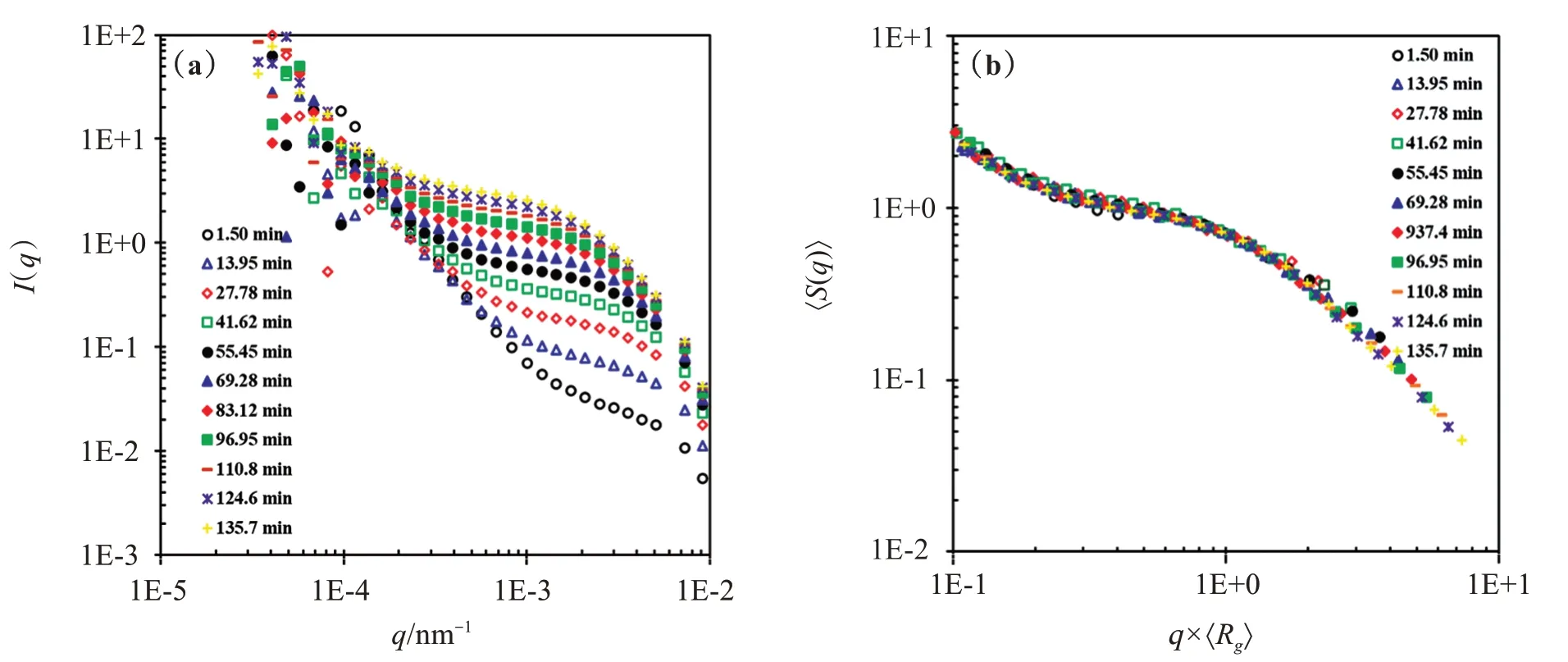
图2 WPI-PAs团聚体的光散射强度曲线随时间的演化曲线（a）与团聚体的归一化平均结构因子与归一化的波矢量的函数关系（b）Figure 2 Typical time evolution of the scattered intensity curves,along the aggregation of the WPI-PAs(a)and the normalized aver‐age structure factor of clusters,at various aggregation times,as a function of normalized wave vector,corresponding to the ag‐gregation systemin(b)

从I(q)−q和〈S(q)〉−q×〈Rg〉曲线得到Df的值，曲线的幂指数区域必须至少跨越2个数量级[8,12]，即团聚体含有50个以上的初级粒子或者〈Rg〉/Rh,0>7且尺寸分布较为单一[14]，团聚体的结构因子才能够得到一个正确的符合幂指数规律的区间。而本文中由于胶粒团聚速度较慢，曲线的幂指数区域没有跨越两个数量级，无法通过此方法求出Df，但是可以根据方程（12）从I（0）对〈Rg〉/Rh,0曲线图求得Df，因为小团聚体一般〈Rg〉/Rh,0>3时，I（0）对〈Rg〉/Rh,0曲线已经符合分形结构的特征[15]：

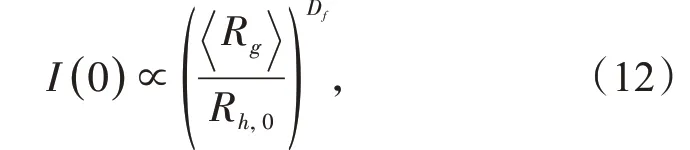
式中：Rh,0=29.3 nm，是初级胶粒的水力学半径，测量方法同〈Rh〉。从公式（12）可以看出，对曲线横、纵坐标取对数，得到的直线斜率就是Df的值。

图3（a）是用公式（12）计算得到q=0处的散射光强度I（0）与〈Rg〉/Rh,0之间关系的时间演化曲线，得到的Df值为2.12，与前面用PBE方程拟合〈Rh〉-t曲线得到的值一致。同时，将得到的Df值和前面拟合出的W值代入到PBE方程中，利用公式（9）和（10）分别计算不同时间团聚体的平均水力学半径〈Rh〉和平均旋转半径〈Rg〉的值[图3（b）中连续曲线]拟合图3（b）中的实验值（点线），可以看到拟合值和实验值非常吻合，得到的λ=0.23，与前文的拟合值非常接近，进一步验证了实验结果的可靠性。

图3 在q=0处的散射光强度与〈Rg〉/Rh,0之间关系的时间演化曲线（a）与〈Rg〉随时间的变化规律的PBE拟合结果（实线曲线）与实验结果（空点点线）的比较（b）Figure 3 Time evolution of the intensity at q=0,I(0),as a function of the corresponding〈Rg〉/Rh,0(a)and PBE simulations(solid line)of the time evolutions of〈Rg〉compared with experiments(open symbols)(b)

4 结论

本研究用广角光散射仪的动态光散射（DLS）和小角光散射仪的静态光散射（SLS）方法，分析WPIPAs在NaCl作用下的团聚动力学和团聚体结构。DLS研究发现，WPI-PAs的团聚速度随时间和NaCl浓度的增加而增大，质量守恒方程（PBE）拟合发现，在所有NaCl浓度下的团聚都是在慢速团聚下进行，即使在接近饱和NaCl浓度时仍没有出现临界聚沉值。拟合得到的Df值全部在2.10左右，说明形成了结构致密的团聚体。选用其中一个NaCl浓度进一步采用SLS分析发现，团聚体的分形维数Df的值确实在2.10左右，而且将DLS拟合得到的参数和SLS实验得到的Df值代入到PBE方程中重新计算得到的〈Rh〉和〈Rg〉的计算值与实验值能够较好吻合，验证了实验结果的可靠性。本文方法能为蛋白质的分析检测以及蛋白质团聚体在多孔材料和药物缓释领域的应用提供可靠的指导。