隐私集合求交技术的理论与金融实践综述

黄翠婷 张帆 孙小超 卞阳

(1.上海富数科技有限公司，上海 200126； 2.中国移动通信集团，北京 100033)

0 引言

随着大数据与人工智能技术的发展与广泛落地应用，数据安全和隐私保护的需求日渐强烈，国内外相关法令法规相继制定，对数据安全与隐私保护相关问题进行严格的规范与引导，例如欧盟的《通用数据保护条例》(General Data Protection Regulation，GDPR)、美国的《加州消费者隐私法案》(California Consumer Privacy Act，CCPA)，以及中国的《中华人民共和国网络安全法》《数据安全法》《个人信息保护法》等。这些法规的制定在不同程度上对大数据、人工智能在各种场景中的数据处理模式提出新的挑战：不能平衡好数据服务与数据安全、隐私保护之间的关系，将严重阻碍大数据和人工智能的进一步发展。为了解决这些挑战，各种安全计算技术在近两年被广泛采用来解决跨机构间的数据合作问题，包括多方安全计算(Secure Multi-party Computation，MPC)、联邦学习(Federated Learning，FL)、可信执行环境(Trusted Execution Environment，TEE)等不同的技术路线。其中，隐私集合求交技术(Private Set Intersection，PSI)被认为是跨机构数据合作的前置步骤，实现跨源数据间的安全融合，也得到了广泛的关注和落地应用。本文从隐私集合求交的技术角度来介绍研究现状和实现机制，并结合典型的金融应用场景对隐私计算技术的具体落地应用进行了研究，最后分析了隐私集合求交技术目前面临的挑战和未来可能的发展方向。

1 隐私集合求交技术

1.1 朴素的隐私集合求交技术

朴素的隐私集合求交的思路是将双方集合中的元素按照约定好的函数规则映射到另一个空间中去，在该空间内接收方可以对映射之后的结果进行匹配。从这种朴素的思路出发，最直接的实现方法是将双方的集合元素逐一经过安全的杂凑函数进行映射，并在杂凑函数的值域内进行匹配。但是这种基于杂凑函数的直接方法在输入集合的熵较小的情况下，恶意的参与方可以通过线下暴力碰撞的方式计算出参与方的所有集合元素。在实际意义下，这种方法不能保护参与方的集合元素安全。

1.2 基于公钥体系的隐私集合求交技术

基于以上朴素的转换匹配空间的思想，运用公钥技术将原集合的元素映射到不同的空间，可以得到不同的基于公钥体制的PSI方案。

1986年，Meadows[1]提出了基于Diffie-Hellman问题的PSI协议，该协议类似于Diffie-Hellman密钥协商协议。双方以各自的输入集合中的元素作为Diffie-Hellman密钥协商中选择出的“随机数”角色，将集合元素映射到随机“会话密钥”空间，接收方在“会话密钥”空间中进行匹配，并获取到最终的交集元素。可以看出，该方案需要双方执行多次的模指数运算(这种代价很高的计算)，因此所得的PSI方案效率并不高。

与基于杂凑函数的算法类似，同样可以在签名空间进行比对。例如基于盲签名，发起方盲化本方输入的每个元素，向响应方的请求盲签名，获得结果并去盲后得到响应方私钥的签名。同时，响应方签名本方的每个元素，并将结果发送给发起方；发起方比对双方的签名结果，获得交集结果。

De Cristofaro与Tsudik[2]在2010年提出了基于RSA盲签名的PSI协议。在该协议中，响应方随机产生RSA密钥；发起方对本方的每一个输入元素进行随机盲化，将结果发送给响应方；响应方使用RSA私钥对盲化结果进行签名并发送给发起方，同时将本方的输入元素用本方私钥进行签名，将结果发送给发起方；发起方对盲化的签名进行去盲，与响应方的签名进行比对，得出交集结果。

基于公钥体制的方案除了转换匹配空间之外，将参与方输入的集合元素看作是多项式的根，多项式可以与输入集合建立映射关系，对于多项式的某些操作可以转换为集合的某些操作。

2004年，Freedman[3]给出了基于不经意多项式取值算法的PSI协议。在该协议中，客户端假设本方的输入集中的所有元素为某一多项式的根，通过多项式插值法求出该多项式的系数。同时，客户端产生出半同态加密方案的公私钥对，用公钥将已获得的多项式系数列表进行加密，并将密文以及密钥全部发送给服务端。服务端根据收到的公钥和密文状态下的系数列表，对本方集合中的每个元素进行密态取值并随机盲化，并将结果返回给客户端。客户端收到反馈数据之后，挨个比对本方集合中每个元素所产生的值，确定本方的元素是否在交集之中。在该方案的执行过程中，需要插值计算产生一个高次多项式，该多项式的次数与客户端的元素个数相同，当客户端的元素较多时，多项式次数较高，产生高次多项式以及对高次多项式的密态计算都会有较大的计算开销。因此，可以将客户端的集合进行随机分桶来降低多项式次数。2016年，Freedman[4]在对集合元素采用杂凑运算来降低协议的计算复杂度，达到改进的效果。

同样是基于不经意多项式取值算法，Kissner与Song[5]运用多项式的特殊数学性质来设计PSI协议。将参与双方的集合运算分别映射到多项式之后，求交集运算等价于求解多项式的最大公因式。基于此思想，参与方将本方的多项式乘以一个随机因式之后展开，将得到多项式系数进行同态加密，然后传输给另一参与方；另一计算方在密态下计算双方多项式和式的值，并逐个元素取值解密，得出解密结果为0的元素为交集元素。

1.3 基于不经意传输的隐私集合求交技术

不经意传输(Oblivious Transfer，OT)是密码协议体系中的一个基础协议，由Rabin于1981年提出[6]。与最原始的概念相比，在更标准化的定义中，发送方拥有若干个输入，接收方输入一个索引下标，该索引下标表示接收方想要得到的结果，在协议过程中这一指标并不会泄露给发送方。最基础的OT协议是2选1 OT。

基于OT的PSI协议需要使用的OT运行实例的数量与PSI双方输入的集合大小有关系，因此OT协议成为大集合PSI方案的主要瓶颈。OT扩展协议的出现[7]，使得大集合PSI方案的落地成为现实。所谓OT扩展协议是指，OT协议在并行数量方面的扩展。具体来说，是用少量的OT协议实例来构造较为大数量的OT协议实例。文献[8][9][10]给出了OT扩展的相关理论结果与实现改进。

2013年，Dong等人在文献[11]中第一次将布隆过滤器引入到PSI中，并与OT扩展结合，使得PSI协议能处理的集合数量首次突破了亿级别。此后，对于布隆过滤器的改进也成为优化PSI协议的一个重要方向。通过改进布隆过滤器，Rindal和Rosulek给出了第一个恶意模型下的PSI协议[12]，这一方案也在200 s时间内完成了两方百万数据量的安全求交。

2016年，在文献[13]中，Kolesnikov等人使用OT扩展来实现不经意伪随机函数(Oblivious Pseudorandom Functions，OPRF)[14]，并且将此概念运用到PSI中，这也成为后续基于不经意传输的PSI协议的主要方向。基于轻量级的OPRF(OPRF底层需要OT扩展来实现)以及基础的布隆过滤器，给出了较为优化的结果。

以上所有PSI协议的实现几乎都是在两个参与方的场景。对于多个参与方的场景，文献[15]中Kolesnikov等人引入了不经意的可编程伪随机函数的概念(Programmable Oblivious Pseudorandom Functions，OPPRF)，并且基于插值多项式、布隆过滤器等技术实现OPPRF。OPPRF要求只对发送者编程进去的集合元素，接收者才可以进行不经意地函数取值，未编程进去的元素，接收者返回随机值。各个参与方之间顺次循环扮演发送方和接收方角色，最终完成交集的结果。

1.4 基于可信执行环境的隐私集合求交技术

PSI近两年新提出的一个技术路线是基于可信执行环境。2019年，百度发布了基于可信执行环境MesaTEE的PSI技术方案[16]。在该方案中，PSI以Intel SGX为信任根的基础进行搭建，Intel SGX提供了根植于CPU的硬件可信和高强度隔离运行环境，PSI的参与方通过远程认证来验证PSI执行环境的可信状态。PSI在集中式的TEE环境中解密后再执行计算，具有显著性能优势和容易支持多方PSI。

1.5 隐私集合交集基数计算技术

与PSI问题关联性较强并且解决方案类似的另一个问题是隐私集合交集基数(Private Set Intersection Cardinality，PSI-CA)问题，即直接求多方输入集合的交集的大小(而非先求出交集，再计数)，并且不会泄露各方集合元素的信息。该问题由Agrawal等人于2003年提出[17]，并且给出了基于判定性Diffie-Hellman假设的构造。运用文献[3]中使用的不经意多项式取值，Hohenberger和Weis构造了一个高效的PSI-CA方案。同样是使用不经意多项式取值的方法，Kissner与Song[5]以及Camenisch和Zaverucha[18]也分别给出了PSI-CA方案。Debnath和Dutta也在PSI-CA的构造方面给出了一系列的成果[19-21]，并给出安全证明。以上方案都是基于两方的PSI-CA协议构造，并且具有线性级别的复杂度。对于多方的PSI-CA(简称MPSI-CA)，Debnath等人基于DDH假设构造的门限同态加密，并且结合布隆过滤器，给出了MPSI-CA的构造[22]。

2 隐私集合求交技术在金融领域的应用

隐私集合求交技术在保护参与方的数据隐私性的前提下完成数据集的交集计算，通常在计算结束，参与方的其中一方或多方只能得到多方数据集的正确交集，而不会得到交集以外其他参与方的任何信息。在实际应用中，尤其是在金融场景，具有很强的应用价值，能够在保护集合隐私不泄露、保持数据控制权的基础上，实现参与方数据之间的匹配，满足业务场景的多种需求。

2.1 隐私集合求交典型实现流程

图1为隐私集合求交的一个典型的实现流程。

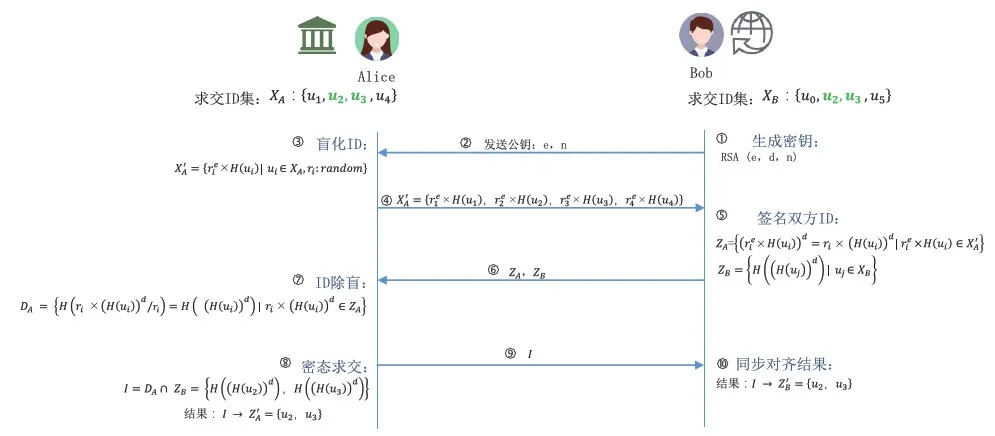
图1 基于盲签名和RSA的PSI参考流程

(1)安全求交的发起方Bob基于RSA生成密钥(e,d,n)。

(2)Bob把公钥e和模n发送给参与方Alice。

(4)Alice把盲化后的样本ID发送给Bob。

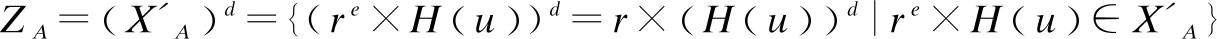
(6)Bob将双方签名后的ID数据集发送给Alice。

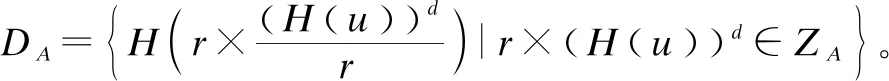
(8)Alice将除盲后的数据集D_A与Bob方签名后的数据集Z_B进行求交，得到双方的交集，并解密得到己方明文的交集ID。

(9)Alice方把密文的交集发送给Bob。

(10)Bob对接收到的密文交集基于己方的公钥进行解密得到己方明文的交集ID。

隐私集合求交技术通常是基于ID来实现交集的计算，即在计算的过程仅通过样本集的ID列参与计算，在求得ID集合的交集后，再同步相对应的特征标签列给其他参与方或是仅在节点内同步特征列为后续的其他计算做准备。而在目前的实际应用中，也衍生出一些新的需求，例如除了不泄露参与计算的集合的ID和特征的基础上，要求集合的基数也不泄露；或者是在隐私集合求交过程中，只返回交集大小，不返回具体的交集ID；或者是在进行集合求交的过程中，增加了集合筛选条件，只返回满足筛选条件的交集。

同时，隐私集合求交技术除了实现原始的求交功能，也根据业务场景的需求进行改进，实现隐私集合求并、隐私集合求补等功能。其中，安全求交是隐私集合求交技术最常用的场景，通过安全求交后得到的交集可以进一步进行其他的联合计算、联合建模等操作。而安全求并一个典型的应用是多方参与的联合建模，因为在联合建模过程中可对缺失值进行处理，在初始的安全融合阶段，需要得到一个大并集来进行后续的处理。而安全求补适用于某些特定的场景，例如营销场景，在营销需求机构与流量方合作联合营销的过程中，流量方用自身数据集合和营销需求方的集合计算出补集(这个补集可认为是营销需求机构的潜在新客)，补集数据在不泄露给对方的基础上进行精准投放。

2.2 隐私集合求交在金融场景的典型应用

隐私集合求交在金融场景的典型应用包括金融联合建模、金融联合统计、金融联合营销等。

2.2.1 金融联合建模

在金融跨机构联合建模场景中，首先需要对各个参与机构的不同样本集进行安全对齐。在传统的方式中，需要把各个参与方的样本汇集到一个中心节点或某一参与方来求出交集，实现样本对齐，再进行模型训练。在建模过程中，各个机构之间用户的重叠度普遍存在不高的情况，例如银行和运营商的数据匹配，不管是从银行等金融机构还是数据源等机构，都不希望暴露非交集部分的用户信息给其他参与方。在这种场景中，隐私集合求交技术可以实现在跨机构建模过程中，各个参与方只能获取交集部分的ID，再通过匹配内部的特征数据，来发起模型训练任务。目前，在基于联邦学习或多方安全计算技术的联邦建模方案中，隐私集合求交技术已经被认为是必不可少的前置步骤。

2.2.2 金融联合统计

在金融行业中，跨机构的联合统计也是安全计算技术的一个典型应用。通过将多方安全计算技术引入到跨机构之间的数据分析、数据统计等场景，可以在不暴露隐私数据的基础上，多方协作完成协同计算。在这个过程中，如果涉及到ID层级的统计分析，则需要通过隐私集合求交技术进行参与计算的数据的对齐，使得只有交集的部分参与跨机构之间的协同计算，非交集部分的用户对于其他参与方均无法获得，从而提升金融场景多方联合统计的安全性。

2.2.3 金融联合营销

在金融联合营销场景中，主要分为存客营销与新客营销两种情况，隐私集合求交技术均可使用于这两种不同场景。针对存客营销场景，金融机构可以通过隐私集合求交技术与外部数据源对存客用户进行客户分群计算，筛选出符合营销条件的存客用户，由金融机构或是外部数据源进行精准的触达营销。针对新客营销场景，金融机构和外部数据源可以通过安全求补技术，来筛选出符合营销条件并且不属于金融机构存客的潜在客群进行拉新营销活动。

基于隐私集合求交技术，还可以应用于营销效果的分析，计算跨机构之间的营销转化率等。例如，有多少用户在浏览广告后申请了金融机构的服务等，通过这种方式在保护用户隐私的基础上更加精准地对营销的效果进行在线评估和营销策略优化。

隐私集合求交技术在很多场景下是自然甚至是必要的需求，随着数据安全和隐私保护的需求日渐普遍，隐私集合求交技术的应用边界必将更加广泛。

3 隐私集合求交技术在金融领域的发展与挑战

隐私集合求交技术主要基于密码学技术来实现，在近几年提出了很多优化实现机制，但在实际落地应用中仍面临着计算效率、安全性、参与方的可扩展性等挑战。

隐私集合求交技术的应用分为离线和实时两种情景，目前一些隐私集合求交技术已能达到亿级对亿级的数据量在小时内完成，这个计算性能能够满足一般的离线多方协同计算的需求，但是面向实时的金融计算场景，在性能方面仍有很大的优化空间，也是影响隐私集合求交技术能否在金融领域被广泛应用的一个重要因素。相比传统的集中式求交，隐私集合求交技术涉及多个节点参与，并要求通过分布式的方式来实现在保护隐私的基础上完成求交计算，这决定了隐私集合求交技术性能的挑战主要在于通信与节点的加解密计算开销。在隐私计算集合求交的性能优化上，除了基本的算法本身逻辑的优化，也需要结合工程化过程中算法流程的最优化设计，例如分片并行处理等，通过技术的手段进行计算加速。通过硬件加速，如采用GPU等，也是目前隐私计算集合求交计算性能优化的一个重要方法。此外，节点通信加速和代码加速，也是有效的优化机制。

隐私集合求交技术主要是为了实现跨机构间数据合作能够在数据安全与隐私保护基础上完成，因此安全性也是隐私集合求交计算的一个重要关心的问题。目前，面向业务场景实现的隐私集合求交方案主要是基于半诚实模型，虽然也有一些恶意模型下的隐私集合求交技术的研究，但恶意模型的解决方案是以高通信与高计算资源为代价，普遍性能较差，难以应用于实际业务场景。此外，在金融场景实际落地应用中，隐私集合求交技术缺乏统一的标准化安全性证明规范，通常以自证清白的方式来证明安全性，增加了安全性验证的难度，从而影响隐私集合求交技术在金融领域的推广。

隐私集合求交技术目前主要是基于两方之间，面向三方及以上的实现方案较少，或主要是通过两两求交之后再求交的方式来实现。这种方式会暴露一部分中间信息，降低隐私集合求交技术的安全性。目前，一些能够实现直接的多方之间的安全求交的技术，普遍与两方的隐私集合求交技术有较大的性能差距，而在金融场景中，三方以上的数据合作却是极其普遍。因此，迫切需要加速隐私集合求交技术参与方可扩展性研究与落地应用。

4 结束语

随着隐私保护的相关法令法规的制定，多方安全计算、联邦学习等隐私计算的相关技术开始被广泛应用在各种应用场景，其中目前落地应用最广泛的是金融等核心行业。金融行业数据化程度高，也是目前跨机构数据协作需求最旺盛的行业，同时金融数据的高隐私性特性也形成了高合规性的要求。隐私计算技术正是通过融合传统的统计计算、机器学习算法与密码学技术来打破数据孤岛，以安全合规的方式来实现跨机构之间的数据合作。隐私集合求交技术作为隐私计算领域的一个子领域，为隐私计算的实际落地应用提供了数据协同的前置步骤，能够更好地满足隐私计算技术的实际落地的全流程安全性要求。此外，基于隐私集合求交计算，可以衍生出多种金融落地应用方案，拓宽隐私计算技术在金融领域的应用边界。

结合目前隐私集合求交技术的技术发展与应用落地现状，未来两三年隐私集合求交技术的研究重点包括：高性能的隐私集合求交技术的研究和设计，打破目前隐私集合求交技术在实时应用场景的性能瓶颈；在恶意模型下的隐私集合求交技术落地应用，通过平衡性能与安全性要求，实现具有高可应用性的解决方案；高扩展性的隐私集合求交技术，包括数据量级的扩展性、参与方的可扩展性等；面向复杂计算场景的隐私集合求交技术研究，如保护集合基数的隐私集合求交技术、高效的隐私集合交集基数计算技术等。

隐私集合求交技术目前在实际落地应用中，仍处于初级阶段，通过性能、安全性、可扩展性的优化，并与实际应用场景深度融合，必将能够在跨机构数据协同合作中发挥更大的应用价值。