全回转起重船压载调拨方案优化决策分析

孟 珣,唐 品,李德江,3*,孙龙龙

(1.中国海洋大学 工程学院,山东 青岛266100;2.山东省海洋工程重点实验室,山东 青岛266100;3.烟台中集来福士海洋工程有限公司,山东 烟台264035;4.青岛瀚海海洋工程设计研究有限公司,山东 青岛266100)

随着海洋开发技术的不断发展,模块化、大型化成为海洋工程建设的主要特点,而起重船作为海洋工程建设中的关键装备,也日趋重型化[1]。起重船按照起重机械的结构形式,可分为固定扒杆式和回转式。对于全回转起重船,其起吊、回转作业时会导致船体纵向、横向倾斜,影响船舶自身安全,随着起重船起重量级的大型化,该问题更为突出[2]。吊装物的重量产生巨大的倾覆力矩,静横倾角可能达到7°～8°,通过反向加载大量压载水以部分抵消吊重产生的倾斜力矩可使船舶处于安全浮态。回转起重机在船的左右舷带载回转时,倾覆力矩在短时间内反向,需要迅速调拨压载水,否则会使船舶倾斜加剧,威胁作业安全[3]。

船舶配载过程需压载系统及压载水加载、调拨的支持,从而保证其安全高效工作,国内外针对船舶配载问题进行了相关研究。夏华波等[4]对遗传算法进行了改进,提出种群全部交叉和分布式动态惩罚函数法等改进机制,对驳船配载中的调载水量分布进行优化,以便在较短时间内完成配载作业。Bara等[5]建立了运行状态的船体受力分析模型,基于图论,提出了吊装货物时压载系统稳性最优控制策略,以降低能耗。刘晓宇[6]以起重船起吊回转工作过程中压载水总调拨量最小为优化目标,考虑稳性要求,建立起重船压载水调拨量优化模型。刘志杰等[7]以起重船舶各压载舱室液位变化量为优化变量,压载舱压载水总调配量最小为优化目标,起重调配过程船体平衡为约束条件,建立了起重船舶压载水调配优化模型。潘伟等[8]提出了一种起重船压载水调节数学模型,实现了在浮态满足规范要求下,起重船作业过程中吊臂匀速回转及压载水总调节量最小的目的。陈伶翔等[9]建立稳性计算模型,对起重机吊载工况进行模拟,分析在艏吊、艉吊和联合吊三种工况下平台在吃水一定时的横纵倾变化,并运用快速调载的方式将平台调平,给出了调平后的配载方案。

上述研究多以压载水总调拨量最小作为单一优化目标,起重机每回转一个小角度确定一次配载方案,在回转大角度时最终确定的配载方案较为复杂,增大操纵难度。因此,本文在起重机起吊重物并做大角度回转时,基于多目标遗传算法,以各个压载舱调载量最大值最小、起重机起吊重物并回转过程中船舶纵倾角最小和横倾角最小作为3个优化目标,以期获得配载方案最优集,并利用基于熵权的TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)方法,以期客观准确地得到最终的方案,为起重船压载调拨提供参考。

1 起重船压载调拨多目标优化及多准则决策方法

1.1 起重船浮态

在随船坐标系Ox′y′z′中,以坐标值(x′G,y′G,z′G)表示船舶重心G的位置,坐标值(x′B,y′B,z′B)表示船舶浮心B的位置(图1),则船体在静水中任意状态下的平衡方程[10]为

式中,W为船舶重量;Δ为排水量;θ为纵倾角,通常以向首部倾斜为正,向尾部倾斜为负;ø为横倾角,通常以向右舷倾斜为正,向左舷倾斜为负。

起重船在作业时,应按照《船舶与海上设施起重设备规范》[11]规定,允许船舶最大纵倾角为2°,最大横倾角为5°。在图1中,Oxyz为固定在地表的惯性坐标系。在惯性坐标系中,重心G的坐标为(x G,y G,z G),浮心B的坐标为(x B,y B,z B),则平衡状态的方程为

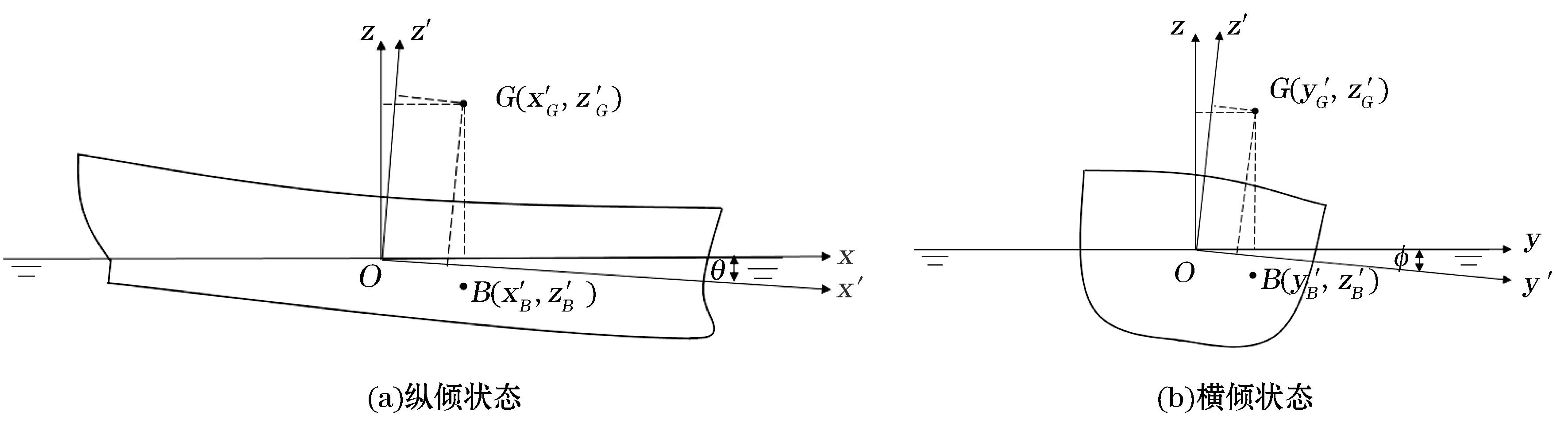
图1 静水中的船舶任意状态Fig.1 Free position of a vessel in the calm water

式中,θ为纵倾角;ø为横倾角;x′G,y′G和z′G为船舶重心在随船坐标系下的纵向、横向与垂向坐标。

1.2 多目标优化

起重船在完成重物起吊和大角度回转作业过程时,在起吊前压载方案的基础上,需要配合吊机作业完成2次压载调拨。本文建立起重船配载方案优化数学模型,利用遗传算法,其中优化目标可为单个目标或多个目标,求解优化模型得到最优解或最优解集。

1.2.1 起吊前加载优化数学模型

由式(1)导出船体在正浮时的平衡方程为

式中,W为船舶重量,Δ为排水量;x′B与y′B为船舶浮心在随船坐标系下的纵向与横向坐标;x′G与y′G为船舶重心在随船坐标系下的纵向与横向坐标。

起吊前的加载方案以船舶初稳性高GM最大为优化目标,利用单目标遗传算法求解得到最优解,优化约束条件的公式为

式中,W为船舶总重量,Δ为排水量;θ为纵倾角,ø为横倾角;0≤G i≤Gmax表示N个压载舱中压载水加载量的约束;表示船舶吃水一定时压载水总量保持不变。

1.2.2 起吊重物时压载调拨优化数学模型

起重船在起吊重物时,需完成一次压载调拨,在压载泵工作功率一定的情况下,各压载舱调拨量最大值决定配载时间,为保证起重机可在较短时间内起吊重物并且船舶处于安全浮态,调拨方案以各个压载舱调拨量最大值最小、平衡状态时船舶纵倾角最小和横倾角最小作为3个优化目标,利用多目标遗传算法求解得到最优解集,优化约束条件的公式为

式中,W为船舶总重量,Δ为排水量;θ为纵倾角,ø为横倾角;0≤M i≤Mmax表示N个压载舱压载水调拨量的约束表示调拨时压载水总量保持不变。

1.2.3 起吊重物回转时压载调拨优化数学模型

从实际全回转起重船的作业工况看,为保证吊物不会出现剧烈的摆动,吊臂应保持匀速回转。起重船起吊重物大角度回转时,相应压载舱的压载泵以一定功率开始调拨压载水,压载舱内的压载水量不断变化,回转至指定位置时,最大调拨量的压载舱压载泵结束工作。为保证配载作业可在较短时间内完成并且船舶在此过程中处于安全浮态,将起重机大角度回转分为S个阶段,调拨方案以各个压载舱调拨量最大值最小、回转过程中各阶段船舶纵倾角最大值最小和横倾角最大值最小作为3个优化目标,利用多目标遗传算法求解得到最优解集,优化约束条件的公式与式(5)一致。

1.3 多准则决策方法

利用多目标优化得到的最优解集,以主观判断和工程经验获得最终的配载方案,缺乏客观性。因此本文引入多准则决策概念,利用基于熵权的TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)方法,客观准确地得到最终的方案。TOPSIS法通过对有限评价方案与理想目标相比较,按与理想目标的接近程度对各个方案进行排序,以此评价现有方案的优劣。在本文中,除了将3个优化目标作为决策属性外,考虑到自由液面对初稳性高的不利影响,在完成压载调拨后,尽可能保证较多的满舱数量,因此将满舱数量作为第四个决策属性,并假定各压载舱内压载水量达到90%即为满舱。

2 算例分析

本文以多功能全回转起重船为研究对象,其船体主尺度参数见表1。该起重船拥有12个压载舱用于压载调拨,左、右舷对称布置6个(图2),编号为5-2P,5-2S,6-2P,6-2S,7-2P,7-2S,8-2P,8-2S,9-2P,9-2S,10-2P和10-2S。压载舱为空间立方体,底部垂向坐标均为3.2 m,顶部垂向坐标均为16 m,各个压载舱矩形底面的长与宽如图2所示,其中6-2P,6-2S,7-2P,7-2S,8-2P,8-2S,9-2P和9-2S压载舱用于调节船舶横倾,5-2P,5-2S,10-2P和10-2S压载舱用于调节船舶纵倾,起重机位于起重船左舷。该起重船构成部分及重心位置如表2所示,其中基平面、中纵剖面和尾部铅垂面的交点作为原点,起重机臂架和偏心转台的重心坐标为起重机未作业时的坐标。

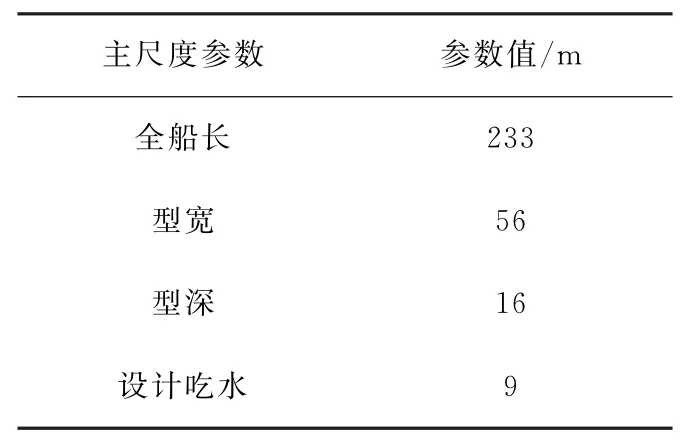
表1 半潜起重船主尺度参数Table 1 Main dimensions of a semi-submersible crane vessel

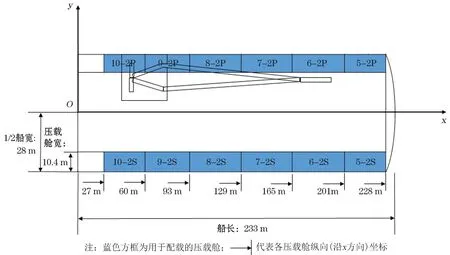
图2 起重船压载舱布置及相关尺寸Fig.2 Layout and related dimensions of the ballast tanks of crane vessel

表2 起重船构成部分及重心位置Table 2 The components and gravity center position of the crane vessel

续表

2.1 起重机起吊前的加载方案

起重机起吊前,船舶吃水为8.7 m。基于船体的三维模型,利用AQWA(Advanced Quantitative Wave Analysis)软件完成静水力计算,正浮时,船舶浮心B在三维模型坐标系中的坐标为(115.090 14 m,0 m,4.603 972 6 m),排水量为90 154.771 88 t,水线面相对x轴的面积二阶矩为2 804 765.5 m4。基于1.2节的优化数学模型,利用MATLAB(Matrix Laboratory)软件编写单目标遗传算法,初始种群为50个,交叉率为0.9,变异率为0.7,迭代次数为200次,求解得到的配载方案见表3,由此得到最大初稳性高为21.021 9 m,相应重心高度为15.470 4 m。

表3 起重机未起吊前配载方案Table 3 The scheme of ballast allocation before crane lifting load

2.2 起重机起吊重物时的配载方案

起重机90°起吊5 000 t重物,配载方案采用6-2P与6-2S,7-2P与7-2S,8-2P与8-2S,9-2P与9-2S,10-2P与5-2P,10-2S与5-2S互拨方式,压载水总量保持不变,此时船舶吃水为9.120 9 m,正浮时船舶浮心B在三维模型坐标系中的坐标为(114.677 86 m,0 m,4.830 325 m),排水量为95 154.771 88 t,水线面相对x轴的面积二阶矩为2 846 263 m4。此时起重机臂架重心坐标变为(37.2 m,49.23 m,127.07 m),起重机偏心转台重心坐标变为(37.2 m,14.1 m,49.2 m),起吊重物的坐标为(37.2 m,54.5 m,68.5 m)。

由式(2)导出,在随船坐标系中,船舶重心的纵、横坐标公式为

式中,x′G,y′G和z′G为船舶重心在随船坐标系下的纵向、横向、垂向坐标;x G与y G为船舶重心在惯性坐标系下的纵向与横向坐标;θ为纵倾角;ø为横倾角。

利用AQWA计算不同纵倾角、横倾角时浮心的坐标,利用拟合程序得到倾斜角θ与浮心x方向坐标值(基于惯性坐标系)的函数关系公式为

式中,x B为船舶浮心在惯性坐标系下的纵向坐标,θ为纵倾角。

同理,利用拟合程序得到倾斜角ø与浮心y方向坐标值(基于惯性坐标系)的函数关系公式为

式中,y B为船舶浮心在惯性坐标系下的横向坐标,ø为横倾角。

采用互拨配载方式时,因为6-2P与6-2S,7-2P与7-2S,8-2P与8-2S,9-2P与9-2S舱室底面积相等,互拨不改变船舶重心在z方向的坐标值;而10-2P与5-2P,10-2S与5-2S舱室底面积相差不大,互拨对船舶重心在z方向的坐标值影响很小,所以起重机90°起吊5 000 t重物时,压载水调配时假定不改变船舶重心在z方向的坐标值,即z′G=9.136 0 m。在惯性坐标系中,平衡状态下,x G=x B,y G=y B,代入式(6)得出在船舶未倾斜处于正浮时,重心和浮心在x和y方向的相对位置与纵倾角θ,横倾角ø的关系公式为

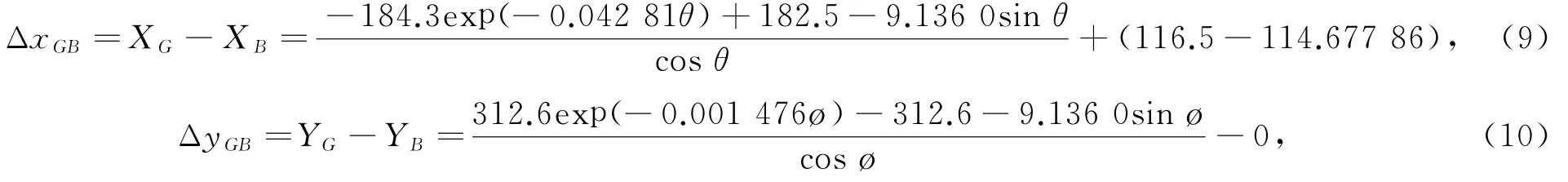
式中,ΔxGB与ΔyGB为在船舶未倾斜处于正浮时,重心和浮心在纵向(x方向)、横向(y方向)的相对位置;θ为纵倾角;ø为横倾角。

基于本文中优化数学模型,利用MATLAB软件编写多目标遗传算法,初始种群为50个,最优个体系数为0.3,迭代次数为200次,停止代数为200,求解得到的压载调拨方案Pareto最优解见图3,图中横、纵倾角均取绝对值。基于本文中多准则决策,利用基于客观熵权的TOPSIS方法对Pareto最优解排序,得到90°起吊5 000 t重物最终的压载调拨方案与候选方案一和方案二,如表4所示。其中各压载舱调拨量最大值的熵权为0.187 1,横倾角的熵权为0.177 9,纵倾角的熵权为0.171 6,满舱个数的熵权为0.463 6。

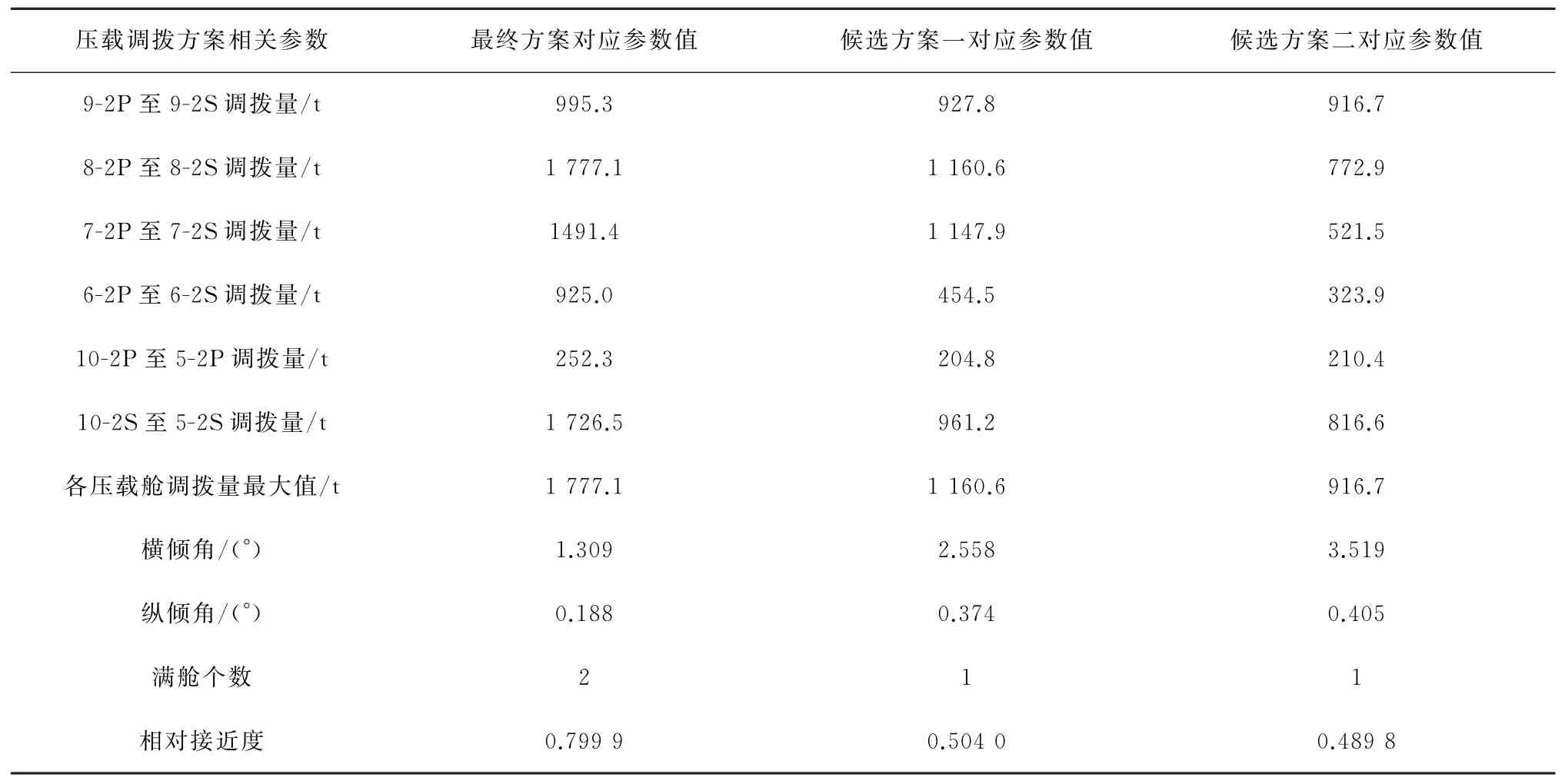
表4 压载调拨方案最优集Table 4 The optimal set of ballast allocation schemes

图3 90°起吊5 000 t重物压载调拨方案Pareto图Fig.3 The Pareto map of ballast allocation scheme for lifting a load of 5 000 t at 90°

基于最终方案和2个候选方案,起重机起吊5 000 t重物逆时针回转90°时,假设不进行压载调拨,在回转过程中船舶横倾角及纵倾角的变化如图4所示,分析表明,起重机90°起吊5 000 t重物后,船舶处于左倾、尾倾状态,逆时针回转90°时,若不进行压载调拨,船体由左倾状态向右倾状态过渡,整个回转过程中船舶横倾角不超过5°、纵倾角不超过2°,满足规范[11]要求。且起吊5 000 t重物后,船体左倾角度越大,完成逆时针回转后右倾角度越小。

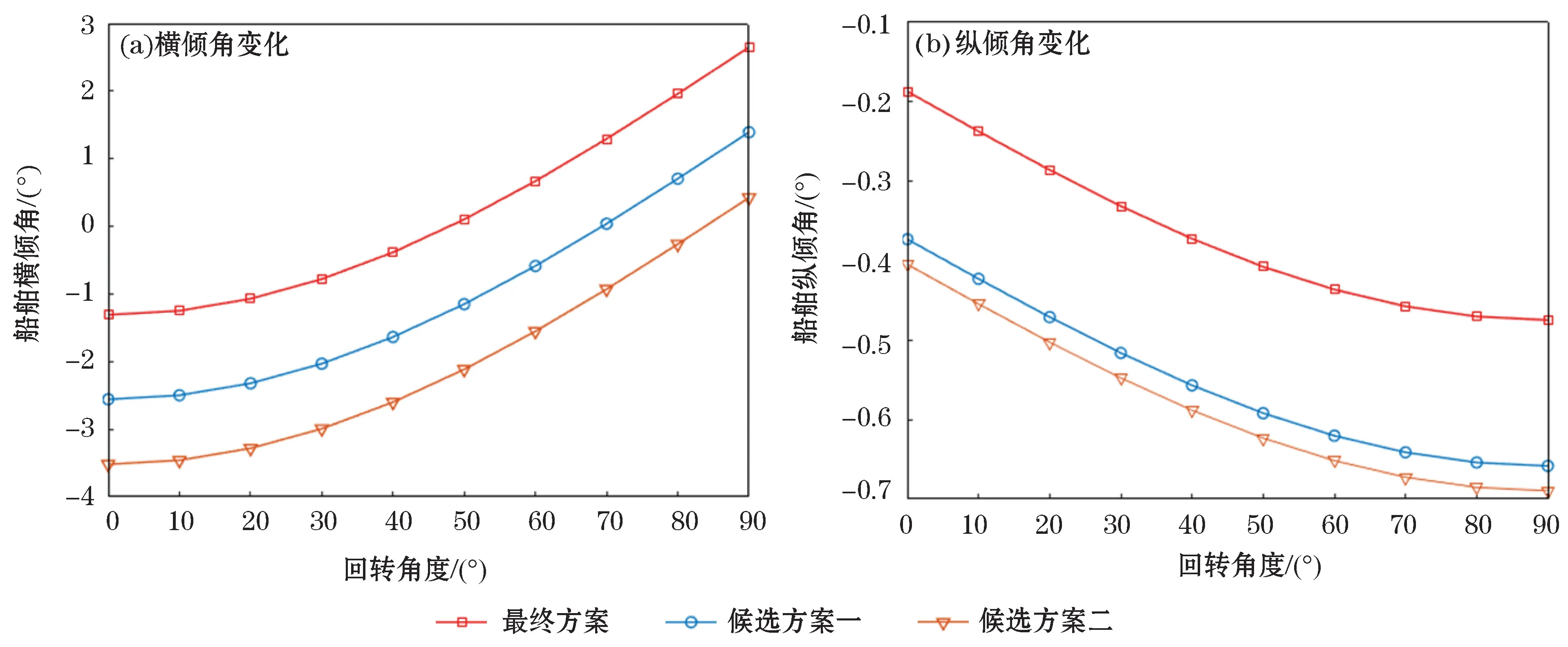
图4 不进行压载调拨时回转过程中船舶横、纵倾角变化Fig.4 Changes of the heel and trim angles of the vessel during rotating at the time without ballast allocation

在实际工程中,为确保起重机安全作业,要求船舶最大横倾角和最大纵倾角为1°,因此根据工程要求,本文修改优化模型中的约束,在其他条件不变的情况下重新完成求解,得到的压载调拨方案见图5,图5中横、纵倾角均取绝对值。利用基于客观熵权的TOPSIS方法对Pareto最优解排序,得到90°起吊5 000 t重物最终的压载调拨方案,见表5。其中各压载舱调拨量最大值的熵权为0.367,横倾角的熵权为0.368 2,纵倾角的熵权为0.261 8,满舱个数的熵权为0。

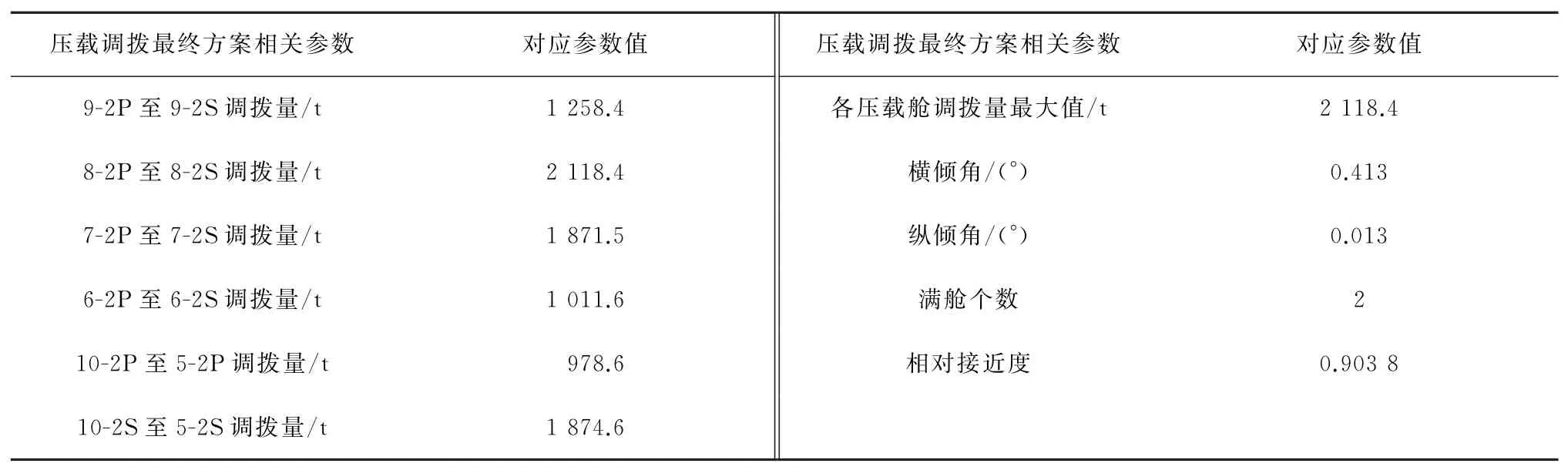
表5 90°起吊5 000 t重物压载调拨最终方案Table 5 The final scheme of ballast allocation for lifting a load of 5 000 t at 90°

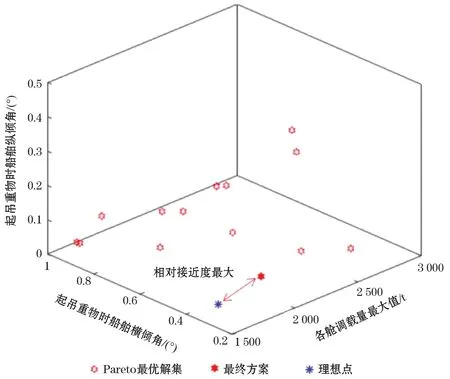
图5 根据工程要求的90°起吊5 000 t重物压载调拨方案Pareto图Fig.5 The Pareto map of ballast allocation scheme for lifting a load of 5 000 t at 90°according to engineering requirements

在90°起吊5 000 t重物时,对比满足规范要求下得到的最终配载方案发现,横、纵倾角不超过1°约束下获得的最终配载方案中,各压载舱调拨量增大,但横、纵倾角均很大程度地减小。

2.3 起重机回转过程中的配载方案

在起重机完成5 000 t重物起吊后,当逆时针回转90°时,配载方案依旧采用互拨方式,逆时针回转90°后起重机臂架重心坐标变为(6.47 m,18.5 m,127.07 m),起重机偏心转台重心坐标变为(41.6 m,18.5 m,49.2 m),起吊重物坐标为(1.2 m,18.5 m,68.5 m)。

本文将90°回转过程分为9个阶段,每个阶段回转10°并计算相应的船舶纵倾角、横倾角,基于本文中的优化数学模型,以9个阶段船舶纵倾角最大值最小、横倾角最大值最小、各个压载舱调载量最大值最小作为3个优化目标,利用MATLAB编写多目标遗传算法,初始种群为50个,最优个体系数为0.3,迭代次数为100次,停止代数为100,求解得到的压载调拨方案,如图6所示,图中横、纵倾角均取绝对值。

图6 起吊5 000 t重物逆时针回转90°压载调拨方案Pareto图Fig.6 The Pareto map of ballast allocation scheme for lifting a load of 5 000 t when rotating 90°counterclockwise

利用基于客观熵权的TOPSIS方法,得到起吊5000 t重物逆时针回转90°最终的压载调拨方案,见表6。其中各压载舱调拨量最大值的熵权为0.329,横倾角的熵权为0.293,纵倾角的熵权为0.378,满舱个数的熵权为0。

表6 起吊5 000 t重物逆时针回转90°压载调拨最终方案Table 6 The final scheme of ballast allocation for lifting a load of 5 000 t when rotating 90°counterclockwise

回转过程中基于最终优化方案进行压载调拨时船舶横、纵倾角的变化如图7所示,分析可知,若要求船舶横、纵倾角不超过1°,在回转过程中不进行压载调拨时,船体横倾角会达到3.6°,不满足要求,而优化决策后船体横倾角最大减小2.727°,纵倾角最大减小0.270°。

图7 回转过程中基于最终优化方案进行压载调拨时船舶横、纵倾角变化Fig.7 Changes of the heel and trim angles of the vessel during the rotating at the time when adjusting the ballast allocation based on the finally optimized scheme

3 结 论

本文以多功能全回转起重船为研究对象,建立了起吊前加载优化数学模型,并利用单目标遗传算法求解获得作业前的压载方案。基于该压载方案,建立了起吊重物时及起吊重物回转时压载调拨优化数学模型,并利用多目标遗传算法求解得到压载调拨方案的最优解集。针对该最优解集,引入基于熵权的TOPSIS多准则决策方法,客观准确地得到压载调拨与吊机作业配合的最终配载方案,以保证起重船安全高效地完成作业。同时得到以下结论:

1)利用AQWA静水力分析可较为准确地获得船舶重心与倾角的关系,为多目标优化提供起重船作业过程中的船体倾角变化;优化将输出多个最优配载方案供实际工程参考。

2)基于熵权的TOPSIS多准则决策方法可结合工程经验和客观性输出最终配载方案,最终配载方案能较大程度地减小船体横倾角,以满足实际工程要求。