非均匀受压圆孔矩形薄板屈曲性能与有效宽度计算方法

姚行友，宋晓庆，郭彦利

(南昌工程学院 1.土木与建筑工程学院2.江西省水利土木工程基础设施安全重点实验室 江西 南昌 330099)

冷弯薄壁型钢构件宽厚比大、截面高效，且制作简单、安装方便，近年来在建筑工程领域、特别是低、多层冷弯薄壁型钢房屋中的应用日益增多。由于建筑设备管线安装、冷弯薄壁型钢龙骨的支撑布置等原因，常在冷弯薄壁型钢墙体立柱和梁的腹板设置不同类型的开孔。腹板开孔对于冷弯薄壁型钢构件的应力分布、屈曲模式、屈曲性能及承载力等均产生了较大的影响。

近年来，国内外学者对于冷弯薄壁型钢开孔构件的屈曲性能和计算方法进行了诸多研究。Moen[1]进行的开孔轴压中长柱的试验表明开孔对构件极限承载力影响较小，而对延性和峰值后反应影响较大，同时对构件的屈曲模式有一定的影响。Moen[2]通过理论分析给出了开孔轴压和受弯构件弹性畸变和整体屈曲应力的半理论半经验简化计算公式。在试验和有限元分析基础上基于未开孔构件直接强度法计算公式，Moen[3]给出了开孔轴压和受弯构件的直接强度法计算公式。何保康[4]通过对 21 根腹板开孔冷弯薄壁 C 型构件的试验研究发现：开孔腹板沿横截面的应力分布是不均匀的，孔两侧的应力通常大于孔上下边的应力；在开孔腹板的破坏历程中，中央截面孔边处一般先于支承边屈服；并给出了与当时冷弯薄壁型钢规范相一致的有效宽度计算公式用于计算轴压短柱的承载力。姚永红、武振宇[5]对有中间加劲肋的腹板开孔冷弯薄壁卷边槽钢构件的受压性能进行了试验和有限元分析，结果表明所有试件均发生畸变屈曲，中长柱试件还伴随有绕弱轴的整体弯曲；腹板孔洞导致构件屈曲模式发生变化，孔洞的存在使试件承载力降低。姚行友[6]通过有限元分析给出了开孔冷弯薄壁型钢轴压构件弹性畸变屈曲应力计算方法。谭政[7]等对腹板开孔冷弯薄壁钢轴压构件畸变屈曲承载力进行了试验研究，结果表明，对于中等长度腹板开孔冷弯薄壁型钢截面轴压构件主要出现畸变屈曲模式；腹板开孔在对构件畸变屈曲稳定承载力有一定的降低作用，采用折减构件有效截面面积的方法可计算开孔构件的畸变屈曲稳定承载力。Moen[8]、赵金友[9-10]分别对开孔冷弯槽形截面梁、开孔冷弯薄壁型钢卷边槽形截面梁畸变屈曲和局部屈曲进行了试验研究，结果表明开孔会降低梁的屈曲承载力，并给出了开孔受弯构件直接强度法的计算公式。从相关研究来看，开孔会降低构件极限承载力，但无论是采用直接强度法还是有效宽度法计算开孔构件的承载力，均需要首先计算开孔板件的弹性屈曲应力或者屈曲稳定系数。

诸多学者较早就对开孔板件的弹性屈曲应力或者屈曲稳定系数进行了研究。El-Sawy和Nazmy[11-12]使用有限元法研究了板件长宽比、孔位置对沿纵向承担单向压力矩形开孔板件的弹性屈曲荷载的影响，认为开孔板件部分不能被当作一个独立的板件进行分析，并建议开孔不得位于端部板件宽度一半的范围内。部分学者[13-15]采用薄壳元研究了简支多孔矩形板的弹性屈曲，结果表明孔的出现会降低或提高临界弹性屈曲应力，同时会改变屈曲半波的数量和长度。Moen[16]通过有限元分析了开孔轴压和受弯板件弹性屈曲性能并给出弹性屈曲应力的计算方法。柳亚华[17]对轴压开孔薄板的弹性屈曲性能进行了分析，并给出了轴压开孔板件弹性屈曲系数的计算方法。

国内外学者对开孔薄板的受力性能研究大都集中在均匀受压或均匀受弯开孔板件的屈曲性能和屈曲系数，还未见非均匀压应力作用下开孔板件屈曲系数计算方法的研究，这极大的限制了采用有效宽度法计算不同荷载形式作用下开孔构件的承载力。鉴于此，本文利用有限元软件ABAQUS对不均匀压应力作用下圆孔薄板的屈曲性能、屈曲系数和极限承载力进行分析，分析板件长宽比、宽厚比、开孔形状、开孔尺寸、开孔间距等对其影响，继而通过有限元结果拟合给出其弹性屈曲系数的建议计算公式，并基于此修正的屈曲系数采用有效宽度法计算不均匀压应力作用下圆孔薄板的极限承载力，为不同荷载形式作用下圆孔构件承载力计算的有效宽度法提供理论依据。

1 非均匀受压圆孔薄板有限元分析模型

1.1 有限元分析模型建立

采用有限元分析软件ABAQUS建立开孔矩形薄板有限元分析模型如图1所示，薄板长、宽、厚度分别为a，b，t，板件宽厚比b/t，圆孔直径为d，孔间距为S，开孔个数为n，圆孔圆心到板件端部距离为Xe。根据文献[17]可知，当开孔位置Xe/b≥2.0时，开孔板件弹性屈曲系数趋于稳定，因此在后续有限元分析中板件的开孔位置均大于二倍的板件宽度。简支开孔薄板模型的边界条件为：对均匀受压板件，在板件四周约束y向自由度，板件纵向一非加载边约束x向自由度，横向两端施加荷载、中截面约束z向自由度；对偏压及纯弯板件，在板件四周约束y向自由度，板件横向两侧加载并约束x向自由度，板件中截面约束z向自由度；同时约定两加载端截面形状保持为直线。沿板件纵向z方向施加线性变化的荷载，若将截面上最大、最小边缘应力分别记为σ1和σ2，以压应力为正，拉应力为负，定义应力梯度系数ψ=σ2/σ1，则截面应力分布为

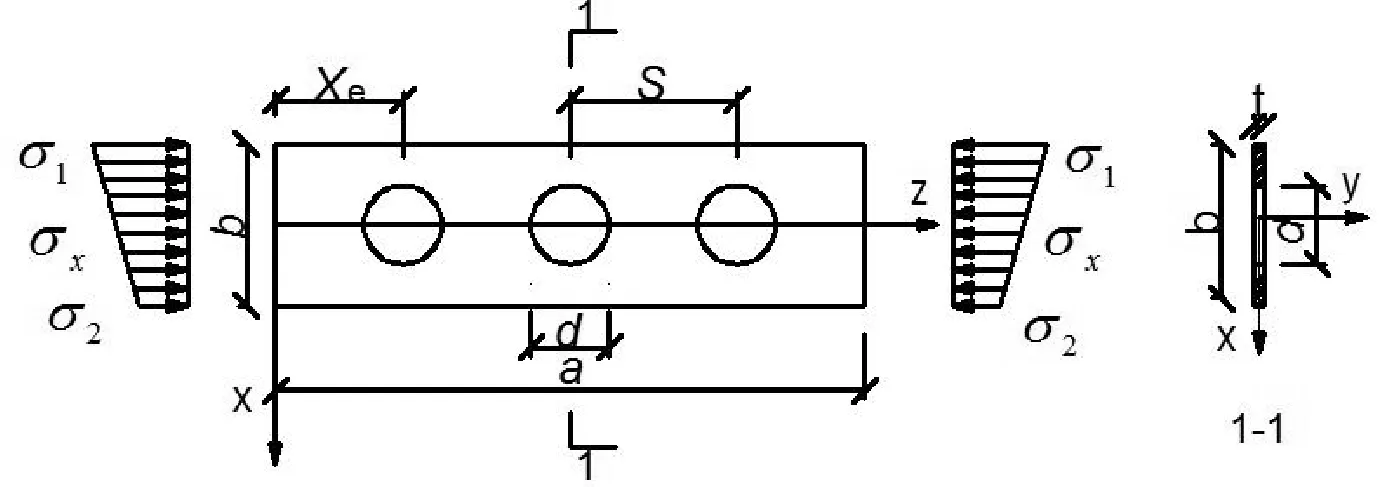
图1 圆孔板件有限元模型

σx=σ1[1-(1-ψ)(x+b/2)/b]，

(1)

式中x为板件宽度方向的坐标。

圆孔薄板分析采用壳单元S4R9，弹性模量E=206GPa，泊松比ν=0.3。极限承载力非线性分析考虑几何和材料非线性，采用理想弹塑性模型，屈服强度取fy=550MPa。初始几何缺陷采用一阶弹性屈曲波形来进行模拟。

1.2 有限元模型的验证

(2)

表1 有限元分析与理论分析屈曲稳定系数结果对比

由表1可知，在线性变化荷载作用下，通过有限元分析的未开孔板件弹性屈曲稳定系数和极限承载力的结果与理论计算结果吻合较好，表明本文有限元分析模型是精确可靠的，并且可以看出板件长宽比对于弹性屈曲系数的影响不大。

2 非均匀受压开圆孔薄板弹性屈曲

2.1 单圆孔

2.1.1 板件宽厚比的影响

取板件长宽比a/b=8，板件中间开孔尺寸d/b=0.5，对板件宽厚比为50，100和150的单圆孔板件进行弹性屈曲分析，得到不同压应力分布作用下板件屈曲系数如表2所示，其中k50、k100和k150分别代表板件宽厚比为50，100和150的屈曲系数。由表2可知，随着板件宽厚比的增大，其弹性屈曲系数几乎无变化，表明板件宽厚比对不同压应力分布作用下圆孔板件屈曲系数影响不大。

表2 不同宽厚比圆孔板件屈曲系数

2.1.2 开孔尺寸的影响

取板件宽厚比b/t=100、长宽比a/b=8，对开孔尺寸d/b由0.1到0.8的单圆孔板件进行弹性屈曲分析，得到不同压应力分布作用下屈曲模式和板件屈曲系数如图2和图3所示。限于篇幅图2仅给出ψ=-1时不同开孔尺寸板件屈曲模式对比，ka为开孔板件有限元分析屈曲系数，kc为未开孔板件有限元屈曲系数。从图2可以看出，随着开孔尺寸的增大，板件由包含开孔的整体局部屈曲(d/b=0.1)转变为开孔边缘的局部屈曲(d/b=0.5)，最终板件只在未开孔位置发生屈曲(d/b=0.8)；由图3可知，随着开孔尺寸的增加，板件屈曲稳定系数均出现先减小后增大的现象，这与图2所示开孔板件屈曲模式的变化直接相关。

图2 ψ=-1不同开孔尺寸板件屈曲模式

图3 不同开孔尺寸板件屈曲系数

2.2 多圆孔

2.2.1 开孔间距的影响

取板件长宽比a/b=8，对开孔尺寸d/b由0.1到0.8，开孔间距S/d由2到10的多圆孔板件进行弹性屈曲分析，得到不同压应力分布作用下板件弹性屈曲系数如图4所示。从图4可知，当开孔间距S/d≥4时，不同压应力作用下多圆孔板件屈曲系数趋于稳定，表明对于多孔板件，若板件开孔间距满足S/d≥4时，板件屈曲系数可采用相同的计算值。

图4 不同开孔间距板件屈曲系数

2.2.2 开孔个数的影响

取板件开孔间距S/d=4、开孔尺寸d/b=0.5，对开3、5、7个圆孔的板件进行弹性屈曲分析，得到不同压应力分布作用下屈曲系数如表3所示，其中k3、k5、k7表示开孔个数分别为3、5、7时的屈曲稳定系数。从表3可知，当板端距及开孔间距不变的情况下，开孔个数对不同压应力作用下板件屈曲稳定系数影响不大。

表3 不同开孔个数板件屈曲系数

2.2.3 开单圆孔与多圆孔板件弹性屈曲对比

取开3个圆孔、开孔间距S/d由4到10、开孔尺寸d/b=0.5，得到不同压应力分布作用下多圆孔板件弹性屈曲系数与单圆孔板件屈曲系数对比如表4所示，其中k多、k单分别表示多圆孔与单圆孔板件屈曲系数。从表4可知，当开孔间距满足一定要求后，不同压应力分布作用下单圆孔板件与多圆孔板件的屈曲系数相差不大，此时开多圆孔板件屈曲系数可按照单圆孔板件屈曲系数取值。

表4 多圆孔板件与单圆孔板件屈曲稳定系数

2.3 屈曲系数计算方法

随着开孔尺寸的增大，不同压应力作用下开孔板件屈曲模式由包含开孔的整体局部屈曲转变为开孔边缘的局部屈曲，最终板件只在未开孔位置发生屈曲，为此对于在不同屈曲模式下的板件屈曲需分别进行考虑，不同压应力作用下圆孔薄板屈曲模式由包含开孔的整体局部屈曲转变为开孔边缘的局部屈曲的临界开孔尺寸如图5所示。

由图5可以得到屈曲模式转变的开孔临界尺寸与压应力不均匀系数相关关系如式(3)：

图5 不同压应力作用圆孔板件屈曲模式变化临界尺寸 图6 圆孔板件屈曲系数与压应力不均匀系数关系

d/b=0.06ψ2-0.14ψ+0.40.

(3)

当开孔尺寸小于该临界时，板件为包含开孔的整体局部屈曲，屈曲系数可按四边简支板进行计算，但需考虑开孔的影响，对开孔尺寸大于此临界值的板件屈曲系数可按照开孔边缘的三边简支板进行计算。

(1)当d/b<0.06ψ2-0.14ψ+0.40时，板件屈曲系数与压应力不均匀系数的关系如图6所示。

根据图6拟合可得圆孔板件屈曲系数建议计算方法如式(4)～(5)：

当0≥ψ≥-1时，

k=(7.8-6.29ψ+9.78ψ2)×[-0.72(d/b)2+0.23ψ(d/b)+0.07(d/b)+1]

(4)

当1≥ψ>0时，

k=(7.8-8.15ψ+4.35ψ2)×[1.06(d/b)2-0.25ψ(d/b)-0.21(d/b)+1]

(5)

(2)当d/b≥0.06ψ2-0.14ψ+0.40时，对于孔边板件屈曲按照三边简支板计算其屈曲系数，有线条程序CUFSM[19]可以给出比较精确的计算结果，因此采用此软件计算不同应力比和长宽比板件的屈曲系数如图7所示，其中a1、b1分别为孔边计算板件的长度和宽度，宽度通过回归分析可得到三边简支板考虑板件压应力比和长宽比的屈曲系数计算公式如式(6)～(7)。

图7 屈曲系数与三边简支板长宽比关系曲线

最大压应力作用于支承边，且1≥ψ≥0时，

(6)

最大压应力作用于自由边，且ψ≥-1时，

(7)

其中ψ为孔边板件压应力不均匀系数。

3 非均匀受压开孔薄板有效宽度计算

3.1 有效宽度法

有效宽度法是计算冷弯薄壁型钢构件和板件极限承载力的基本方法，在给出圆孔板件在不同压应力作用下弹性屈曲系数计算公式的基础上，即可采用GB50018—2002《冷弯薄壁型钢结构技术规范》[20]有效宽度公式计算不同压应力作用下开孔板件的有效宽度，进而计算其极限承载力，计算的承载力不得大于开孔板件净截面承载力。

圆孔板件截面有效宽度分布按图8计算，板件受压区宽度为bc，受压板件有效宽度为be，其中be=be1+be2，be1和be2按照GB50018—2002《冷弯薄壁型钢结构技术规范》[20]对于板件有效宽度的分布规定计算，且有效宽度不大于板件净截面宽度。

图8 板件截面有效宽度分布示意图

3.2 非均匀受压开孔薄板极限承载力

取板件长宽比a/b=3，对宽厚比b/t从20到200、开孔尺寸d/b由0.1到0.8的线性变化荷载作用下圆孔薄板极限承载力进行有限元分析和有效宽度法计算，得到不同压应力作用下圆孔板件极限承载力与宽厚比的关系如图9所示，其中有限元得出的结果采用散点表示，建议有效宽度计算曲线采用实线表示，My、Ny为板件毛截面极限强度，M、N为有限元和建议方法得出的板件极限承载力。

根据图9可知，随着板件宽厚比的增大，非均匀受压圆孔板件极限承载力相对毛截面强度先保持不变，随后逐渐减小；当开孔尺寸较小时，开孔尺寸对于不同压应力分布作用下的板件极限承载力影响较小，但随着开孔尺寸的增加，板件承载力减小明显；通过建议方法得出的极限承载力与有限元分析结果吻合较好，表明建议计算方法具有较高精度。

图9 有效宽度法计算圆孔板件极限承载力对比

3.3 非均匀受压圆孔薄板极限承载力计算可靠度

建议有效宽度法计算得到的开孔板件极限承载力Nd、Md与有限元分析得出的板件极限承载力Na、Ma对比如图10所示，统计结果如表5所示。由图10和表5可以得出，不同压应力作用下不同开孔尺寸板件采用有效宽度法计算板件极限承载力与有限元计算结果吻合较好，计算结果与有限元结果之比的均值和变异系数分别为0.99167和0.01472，表明建议计算方法具有较好的精度。

表5 建议计算方法与有限元分析结果统计分析表

图10 建议计算方法与有限元分析极限承载力对比

4 结 论

采用有限元分析软件ABAQUS对不同压应力作用下圆孔薄板屈曲性能、屈曲系数和极限承载力进行分析，得出以下结论：(1)板件长宽比和宽厚比对于板件弹性屈曲系数影响较小；当板件开孔间距满足一定限值时，多孔板件与单孔板件弹性屈曲系数相差很小。(2)随着开孔尺寸的增加，板件屈曲模式由包含开孔的整体局部屈曲转化为开孔边缘的局部屈曲，开孔板件弹性屈曲系数先减小后增大。(3)当开孔尺寸小于临界尺寸时，可按照四边简支板计算屈曲系数，当开孔间距大于临界尺寸时，可按照开孔边缘的三边简支板计算屈曲系数；通过有限元和有限条分析结果回归分析给出了圆孔板件弹性屈曲系数建议公式。(4)随着板件宽厚比增大，当开孔尺寸较小时，开孔尺寸对于不同压应力分布作用下的板件极限承载力影响较小，但随着开孔尺寸增加，板件承载力明显减小；基于建议的不同压应力作用下开孔板件屈曲系数计算方法，采用有效宽度法计算圆孔板件极限承载力与有限元分析结果吻合较好，表明有效宽度法可用于不同压应力作用下开孔板件的极限承载力计算。