输电线路爆破除冰动态特性*
2021-07-09谢东升史卓鹏智生龙史淋升李海涛
谢东升,孙 滔,史卓鹏,智生龙,史淋升,李海涛
(1. 国网山西省电力公司经济技术研究院,山西 太原 030002;2. 中北大学理学院,山西 太原 030051)
电力系统是重要的生命线工程,保证它的安全稳定运行具有重要意义。输电线路覆冰是威胁电力系统安全的重要因素之一,严重覆冰造成的线路过载荷和脱冰引起的导线舞动可能导致相间闪络、金具损坏、跳闸停电等故障,甚至断线倒塔等严重事故[1-2]。因此,覆冰输电线路的除冰防治技术是电网建设中急需解决的重要课题之一。
目前,实际应用的输电线路除冰方法主要有热力融冰、机械除冰和被动除冰三类[3]。热力融冰是利用附加热源或导线自身发热,使冰雪无法在导线上积累生长或使覆冰融化,热力融冰虽然除冰效果明显,但换流设备费用高且能耗较大;机械除冰利用机械外力使导线上的覆冰破碎脱落,除冰能耗小、费用低,但除冰效率低且需要人工参与[4];被动除冰通过在导线上安装阻雪环、平衡锤等装置,在覆冰达到一定厚度时,在风力、温度和重力等作用下使覆冰自然脱落,该方法除冰偶然性大,无法实现可靠除冰。此外,机器人除冰[5]、激光除冰[6]、超声波除冰[7]等除冰技术也取得了一定的成效,但目前尚缺乏一种经济高效、操作简便的除冰技术。
近年来,宋巍等[8]、谢东升等[9]提出了将线性装药预设在输电线路上,通过爆破的方法去除部分线路覆冰的新思路,并通过小尺寸覆冰输电线的爆破实验和数值模拟研究了药量和装药间距对除冰效果的影响,初步验证了爆破除冰的可行性,但未考虑除冰时脱冰振荡对输电线路的影响。覆冰脱落会引发输电线大幅振荡,可能会诱使其他位置的覆冰陆续脱落,除冰不当容易引发安全事故,因此有必要进一步对爆破载荷作用下输电线的动力效应进行研究。
目前,已有实验[10-12]和数值模拟[13-15]对输电线路覆冰脱落的一系列研究,主要针对输电线覆冰自然脱落的情形,对爆破载荷作用下线路脱冰的研究却鲜有报道。本文中,设计单档输电线爆破除冰模型实验,使用实际的钢芯铝绞线、钢绞线和光纤复合地线,采用爆破方式将输电线的人工覆冰部分去除,模拟输电线在爆破载荷作用下的脱冰振荡。测量覆冰脱落过程中的档中位移和端部张力,得到输电线爆破除冰的动力特性。此外,利用有限元方法对实验工况进行数值模拟,将模拟结果与实验数据进行验证,在确定模拟方法合理性的基础上,进一步利用模拟模型研究脱冰位置对输电线爆破除冰动力特性的影响。
1 实验过程
设计了档距为50 m 的孤立档输电线路爆破除冰模型,输电线采用2根LGJ-240/30型钢芯铝绞线、1根GJ-50钢绞线和1根OPGW-24B1-50光缆,输电线有关参数见表1。输电线两端串入拉力传感器悬挂在两侧的水泥电杆(导线通过横担悬挂)上,在输电线档中测点引出细钢丝绳,连接测点正下方固定在地面的拉线位移传感器,实验中钢丝绳始终处于拉紧状态。利用拉力传感器和位移传感器即可记录除冰过程中输电线的动张力和档中位移的变化情况,传感器及安装位置如图1所示,实验模型如图2所示。

图1 传感器及安装Fig.1 Installation of sensors

图2 实验模型Fig.2 Experimental model
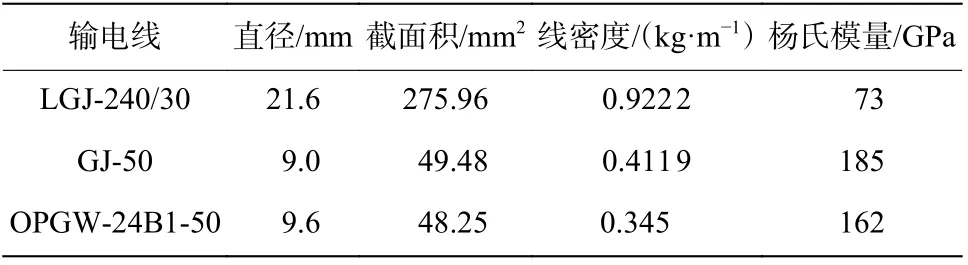
表1 输电线物理参数Table 1 Physical parameters of transmission lines
拉线位移传感器为EY503-5000系列,量程5 000 mm,传感器精度5 mm;拉力传感器为STC-1 500 kg,并利用DH3820高速静态应变测试分析系统采集并输出实验数据,采样频率为50 Hz。
在输电线爆破除冰实验中,先在输电线指定位置敷设导爆索,然后采用人工方式使输电线表面真实覆冰,当覆冰达到一定厚度时通过引爆导爆索去除单根输电线指定位置的覆冰,观察除冰效果及输电线振荡对线路其他位置覆冰的影响,并测量脱冰振荡过程中输电线位移和张力的变化。将导爆索敷设在导线1、地线3和光缆4上,导线2不敷设导爆索,用于观察同档输电线爆破除冰时对该导线覆冰的影响。自然条件下,在较长线路进行人工覆冰很难准确控制覆冰的均匀程度,不便于在相同覆冰条件下进行重复实验,因此分别对三种输电线进行一次爆破除冰实验,通过有限元方法对实验工况进行模拟验证,再进一步利用数值模拟研究爆破位置对动态特性的影响。实验中,为消除爆破位置特殊性对实验结果的影响,输电线上的导爆索采用随机敷设,导线、地线和光缆分别间隔敷设3段、2段和1段导爆索,同一输电线上导爆索之间使用导爆管连接,且通过导爆管雷管进行引爆,输电线上导爆索敷设位置如图3所示,实验工况见表2。
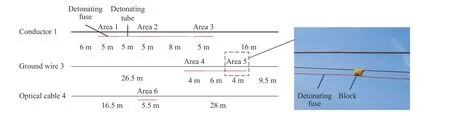
图3 导爆索敷设Fig.3 Setting of detonating cord

表2 实验工况Table 2 Conditions of experiment
采用塑料导爆索太安装药(PETN),外径为5 mm,装药线密度约为11 g/m。导爆索等间距平行敷设在导线下侧,间距为50 mm。导爆索敷设完成后,对输电线进行人工覆冰。在室外环境−15~−10℃条件下,利用高压喷雾装置在线路附近缓慢均匀喷射0℃水雾,连续作业2~3 h,完成模型线路覆冰。由于人工覆冰的线路较长,且覆冰情况受气温、风速等气象条件的影响,线路覆冰并不均匀,厚度最大25 mm、最小10 mm,且形成了冰挂,类似冻雨天气下输电线上形成的雨凇,如图4所示。为与预敷导爆索的输电线自然覆冰情况相符,在人工覆冰过程中未对导爆索进行防护,因此导爆索表面也被覆冰包裹。覆冰完成后,采用单点起爆方式对输电线进行爆破除冰实验,观察各工况下爆破除冰效果,并获得了测点位移和动张力的时程响应。

图4 架空线表面人工覆冰Fig.4 Artificial icing on surfaceof overhead transmission line
2 有限元数值模拟
为了对实验结果的准确性进行验证,进一步分析实验现象以及爆破载荷作用下覆冰脱落的动力效应,使用有限元软件ABAQUS对实验线路进行建模,通过数值模拟对各实验工况输电线档中位移和端部张力进行比较验证;进一步研究除冰位置对输电线脱冰动力效应的影响,并与相同条件下自然脱冰的动力效应进行对比分析。
在有限元软件ABAQUS中,采用梁单元模拟角钢横担,采用不可压缩混合杆单元T3D2H 模拟输电线,忽略水泥电杆的变形并简化为刚体,采用附加冰单元法模拟输电线覆冰脱落,忽略覆冰的不均匀性,覆冰截面形状简化为等截面圆环,用B31管梁单元模拟,冰单元与导线单元采用共节点绑定,覆冰密度设为0.92 g/cm3,弹性模量设为1 GPa。按照实验模型相关参数信息建立有限元模型,并依据覆冰前测量的输电线档中弧垂(见表3)对线路进行找形分析,确定输电线自重作用下的形态。再在输电线模型上添加覆冰单元,根据覆冰前后档中弧垂的变化,确定了覆冰单元的等效厚度以及输电线覆冰后的形态。

表3 覆冰前后输电线档中弧垂及等效覆冰厚度Table 3 Sag of mid-point and equivalent thickness of transmission linebefore and after icing
模拟中,爆破载荷采用在单元节点上施加爆炸三角波载荷实现,三角波载荷利用CONWEP[16]方法计算得到,忽略了导爆索覆冰对爆炸效果的影响。该计算方法通过装药量和爆炸传播距离得到爆炸载荷的峰值以及持续时间。实验所用导爆索装药密度为11 g/m,导爆索与导线的间距为50 mm,计算得到简化爆炸三角波的峰值为80 kN/m2,正压持续时间约为20µs。
爆破载荷作用下覆冰脱落与否采用内聚力黏附力判定准则[17]进行判别,即覆冰受到的铅垂方向惯性力大于覆冰与输电线接触面的黏附力或覆冰内部的内聚力时脱离输电线。加速度形式的覆冰脱落判定准则为[17]:

式中:Dcable为输电线的外径(m);D为覆冰输电线的总外径(m);τad和τco为覆冰单元的黏结应力和内聚应力(Pa);ρice为覆冰密度(kg/m3)。当覆冰的铅垂方向加速度达到临界加速度acritial时,判定覆冰单元失效。根据实验中输电线的相关参数,且人工覆冰的内聚强度和黏结强度分别取0.03和0.2 MPa[18],由式(1)可计算得到导线、地线和光缆的临界加速度acritial分别为8 382、8 439和8 409 m/s2。为充分考虑脱冰对输电线路的影响,出于安全考虑,模拟中选三者最小值(8 382 m/s2)作为覆冰脱落准则的临界加速度。
模拟中,覆冰脱落判定通过ABAQUS软件中的场变量子程序USDFLD来实现,将式(1)作为判定条件写入自定义子程序,作为覆冰单元脱落与否的判定。有限元分析过程中,子程序通过调用主程序中各单元的节点位移和时间增量,计算该时刻覆冰单元的加速度,并与设定的临界加速度进行比较,以此决定覆冰是否脱落。进一步,子程序将判定为脱落的覆冰单元密度和刚度变为零,从而实现输电线覆冰载荷的改变。
基于建立的实验线路有限元模型,模拟输电线自然脱冰时,覆冰脱落采用单元生死的方法实现,即在动力分析中,使用关键字Model Change使脱冰区域的覆冰单元失效,且模拟时间步长为0.01 s[19]。
3 结果与分析
3.1 除冰效果
三种工况的实验结果表明,在除冰线路振荡停止后,输电线爆破区域的覆冰完全去除,非爆破区域的覆冰依然附着在输电线上。观察脱落的覆冰可以看出:爆破区域迎爆面的覆冰在爆破作用下直接粉碎;且覆冰内部形成了贯穿型裂纹,背部覆冰以块状解体脱落;非爆破区域的覆冰仅产生了细微裂纹,线路振荡并未使其脱落,即未发生诱发脱冰现象,如图5所示。此外,除冰时的爆破作用也未引起临近输电线的覆冰脱落。爆破除冰后输电线表面未发现任何可见伤痕,说明导爆索爆炸载荷及导爆索覆冰破碎形成的颗粒并未对输电线表面造成损伤。

图5 爆破后的线路覆冰情况Fig.5 Icing situation of overhead transmission line after blasting
各工况的模拟结果也显示仅爆破区域的覆冰发生脱落,脱冰情况与实验结果相吻合。以工况3为例,图6为爆破除冰过程中不同时刻导线加速度随位置的变化曲线。在起爆时刻爆破区域覆冰的加速度达到了233 km/s2,远大于覆冰脱落的临界加速度8 382 m/s2,因此爆破区域覆冰脱落失效;除冰振荡过程中非爆破区域输电线加速度在8.29 ms时达到最大值108.8 m/s2,小于临界加速度,所以输电线振荡未引起非爆破区域的覆冰脱落。

图6 不同时刻导线加速度随位置的变化Fig.6 Acceleration curvesof conductor with position at different times
3.2 跳跃高度和动张力
对爆破除冰过程中输电线的跳跃幅值和端部动张力进行分析,除冰开始时刻设置为1 s。图7~9为三种工况输电线的档中位移和动张力曲线,图中同时给出了数值模拟结果。由图可见:档中位移模拟曲线与实验结果基本吻合,模拟得到的跳跃幅值与实验值接近,误差均小于6%;动张力模拟结果在脱冰振荡初期与实验结果符合较好,动张力峰值及出现时刻与实验结果较一致。这说明,除冰过程中导爆索覆冰破碎对输电线动态特性的影响较小,可忽略影响。模拟结果与实验的差异主要因模拟中采用均匀覆冰模型及对爆破载荷进行简化所致。

图7 工况1档中位移和端部张力Fig.7 Mid-point displacement and end tensions under condition 1

图8 工况2档中位移和端部张力Fig.8 Mid-point displacement and end tensions under condition 2

图9 工况3档中位移和端部张力Fig.9 Mid-point displacement and end tensions under condition 3
爆破除冰时,爆破作用使爆破区域的覆冰脱落,由该区域覆冰而蓄积在输电线中的弹性势能得到释放;另外,爆破载荷的冲击作用使爆破区域输电线获得了向上的初始速度。两方面的作用使输电线快速向上运动,运动过程中弹性势能、动能和重力势能相互转化,引发输电线往复振荡,与相同条件的自然脱冰相比,爆破冲击作用使输电线的振荡更剧烈。由图7~9可知,输电线的跳跃幅值及动张力最大最小值均出现在第一个振荡周期内,档中最大反向位移明显大于覆冰后的静态位移,相对应地,动张力峰值与静态张力相比也有显著增大。
3.3 爆破位置对动态特性的影响
自然脱冰条件下输电线跳跃幅值及动张力幅值均随脱冰量增加而增大[20-21],而爆破除冰时输电线动力效应较自然脱冰更显著,因此采用爆破方法除冰时单次脱冰量不宜过大。当脱冰量一定时,为确定更安全的爆破除冰方式,有必要分析爆破位置对除冰动态特性的影响。
基于建立的实验线路有限元模型,参考实验工况的爆破长度,选取爆破除冰量为20%,覆冰厚度设为12.5 mm,模拟了不同位置施加爆破载荷的除冰过程,并与相同条件下自然脱冰的模拟结果进行对比。
比较两种脱冰方式下输电线的跳跃幅值,如图10所示。其中,输电线脱冰位置和跳跃最高点位置为归一化后的数值,即为脱冰段中点到最左端的距离与档距的比值。两种脱冰方式下输电线的跳跃幅值随脱冰位置的变化趋势较相似:脱冰位置不在端部时,跳跃最大点均出现在脱冰段中点附近,且不同脱冰位置跳跃幅值接近;脱冰位置在端部时,跳跃最大点位于脱冰段靠近档中一侧边缘附近,且跳跃幅值最小,这是由于靠近挂点处输电线刚度较大。相同位置脱冰时,爆破除冰的跳跃幅值均大于自然脱冰,且除冰位置在端部时,爆破作用使跳跃幅值增长最明显。三类输电线中,地线和光缆重量较轻,爆破作用对跳跃幅值的影响更显著,与相同位置自然脱冰相比跳跃幅值增幅均超过了40%,最大增幅超过了110%,而导线最大增幅仅为26%。

图10 不同脱冰位置输电线的跳跃幅值Fig.10 Jumping amplitude of conductor at different de-icing positions
图11为两种脱冰方式下动张力峰值随脱冰位置的变化。由图可知,爆破除冰时动张力峰值随脱冰位置的变化趋势与自然脱冰时相似,即脱冰位置越靠近档中,动张力峰值越小。相同位置脱冰时,爆破除冰的动张力峰值均大于自然脱冰;而脱冰位置对两种方式动张力峰值的变化幅值影响较小,各工况下动张力峰值的变化均在4.5%~10.5%。除档中位置外,三种输电线其他位置爆破时动张力峰值均大于除冰前的静态张力。

图11 不同脱冰位置输电线动张力峰值Fig.11 Peak values of dynamic tension of transmission line at different de-icing positions
4 结 论
建立了档距为50 m 的孤立档输电线路模型,进行了爆破除冰实验,利用有限元软件对实验工况进行了模拟,实验和模拟结果一致,验证了模拟方法的正确性。在此基础上,研究了20%脱冰量的情况下,脱冰位置对输电线路动态效应的影响,得到以下结论。
(1)对于雨凇及黏结强度大的覆冰,适当条件下进行爆破除冰,只会引起输电线爆破区域的覆冰发生脱落,利用此性质,可以控制输电线的脱冰量,避免由于不可控的诱发脱冰造成事故。
(2)爆破除冰时,输电线的跳跃幅值及动张力最大、最小值均出现在第一个振荡周期内,档中最大反向位移大于覆冰后的静态位移。
(3)输电线爆破除冰的跳跃幅值均大于相同位置的自然脱冰,跳跃幅值随位置的变化趋势与自然脱冰相似。三种输电线中,地线和光缆的跳跃幅值受爆破作用影响更显著。
(4)爆破位置越靠近档中,输电线动张力峰值越小。相同位置除冰时,爆破作用使动张力峰值大于自然脱冰的,且增长程度受脱冰位置影响较小。除档中位置外,输电线爆破除冰的动张力峰值均大于除冰前的静态张力。
