基于小波变换和连续投影算法的黑土有机质含量高光谱估测

肖艳，辛洪波，王斌，崔利，姜琦刚

(1.长春工程学院勘查与测绘工程学院，长春 130012；2.长春市测绘院，长春 130021；3.吉林大学地球探测科学与技术学院，长春 130026)

0 引言

黑土是宝贵的土地资源，有机质含量的多少是反映土壤肥力、状态和退化程度的重要指标[1-2]。传统土壤有机质含量测定基于化学分析方法，步骤繁琐，耗时费工，很难实现实时检测。近年来，可见光/近红外光谱分析技术以其快速、简便、无污染、不破坏等特点，正逐步成为估测土壤有机质含量的新型有力工具[3]。

采用合适的光谱预处理和波长选择方法不仅能提高土壤参数定量模型的估测能力，还能简化模型，减少计算量[4]。在现有光谱预处理方法中，小波变换在信号去噪和数据压缩方面具有独特的优势[5]。王延仓等[6]结合小波变换和偏最小二乘法估测土壤有机质含量，结果表明小波变换在一定程度上提高了土壤光谱对有机质含量的估测能力；李旭青等[7]利用小波变换选取具有异常光谱特征的奇异点，并采用反向传播神经网络模型对水稻冠层重金属含量进行反演，取得了较好的效果。仅依赖小波变换的结果建模，参与的变量依然较多，存在的大量冗余信息不仅会降低建模速度，而且可能会影响模型的精度。因此仍需一种有效的手段从小波变换结果中进一步筛选出最优变量。常用的波长选择方法有相关系数法、回归系数法、载荷值法、退火算法、遗传算法和连续投影算法(successive projections algorithm，SPA)。相关系数法、回归系数法和载荷值法的阈值大多根据主观经验进行选择，而退火算法和遗传算法的搜寻过程非常耗时,且不稳定[8]。SPA算法能大大减少建模所用变量的个数 ,且计算效率较高，已被广泛用于可见/近红外光谱特征波长的选择。章海亮等[9]和Peng等[10]都利用SPA算法选取建模变量，在保证精度的同时大大降低了模型的计算量。

综上，本文尝试在黑土有机质含量高光谱估测中引入小波变换和SPA算法，即首先采用小波变换对土壤光谱进行降维去噪，然后利用SPA算法从小波变换结果中筛选出最优变量，最后基于最优变量，分别利用偏最小二乘(partial least squares，PLS)和支持向量机(support vector machine，SVM)方法建立估测模型，以验证小波变换和SPA算法的结合在黑土有机质含量高光谱估测上的有效性。

1 供试样本及光谱获取

1.1 土壤样品采集

2014年5月5日—2014年5月10日，根据第二次土壤普查绘制的1∶100万黑土分布图，在黑龙江省黑河市嫩江市、北安市、五大连池市，绥化市以及吉林省长春市德惠市、榆树市的黑土带内，共采得61个土壤样本，采样点分布情况如图1所示。将土样置于室内，自然风干、研磨、过2 mm筛后，把每个样本分成2份，一份用于光谱测量，另一份用于化学分析。土壤有机质的测定采用重铬酸钾容量法。将61个样本分为2组，每间隔3个样本取1个样本作为验证样本，其余作为建模样本，供试样本有机质含量描述性统计如表1所示。

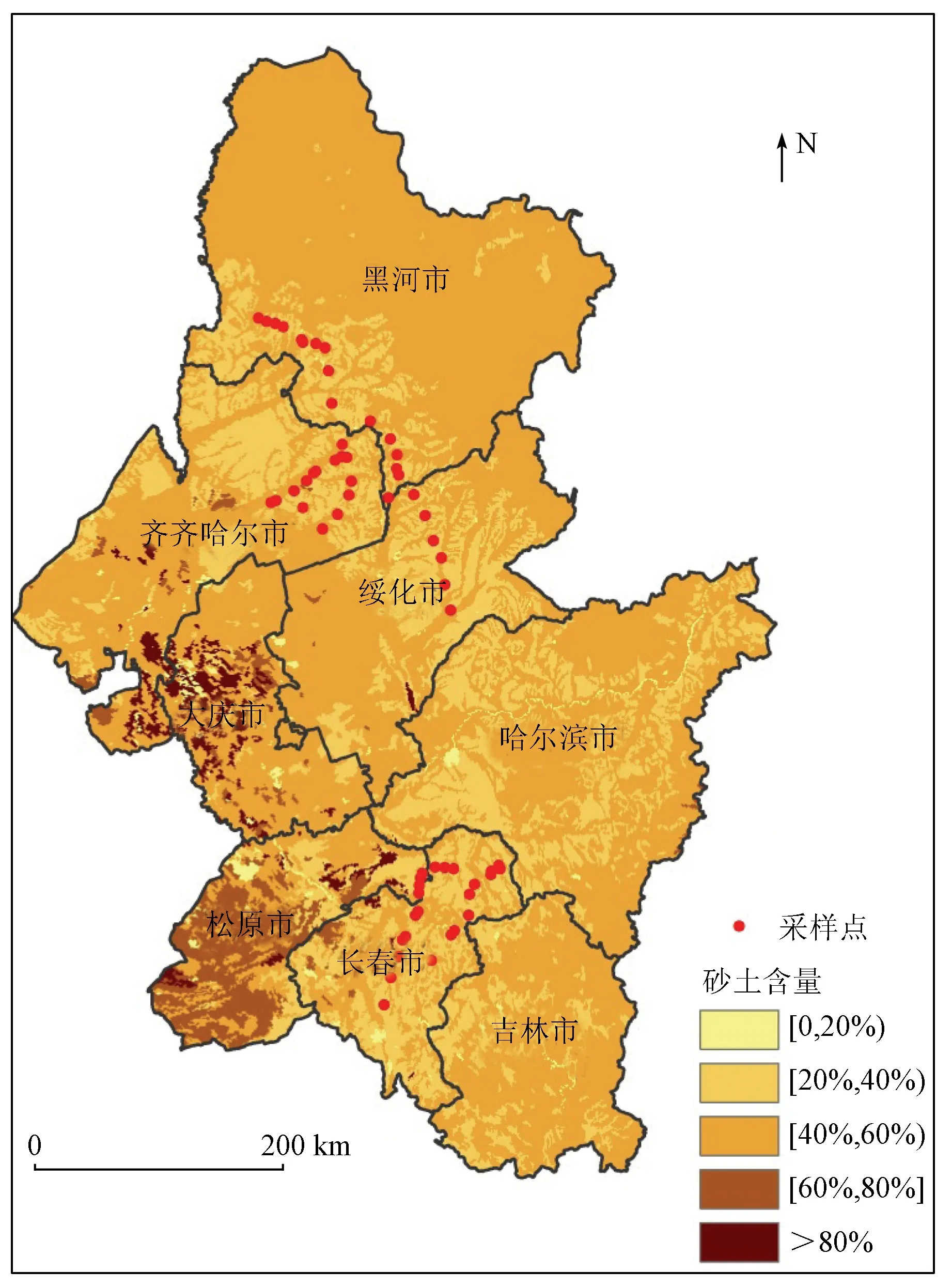
图1 采样点分布图Fig.1 Distribution map of samples

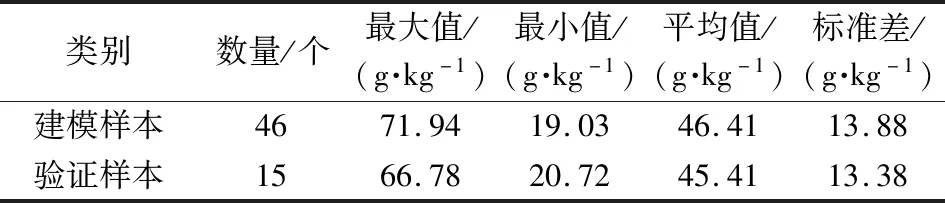
表1 土壤样本有机质含量描述性统计Tab.1 Descriptive statistics of soil organic matter content

1.2 光谱数据采集与预处理

光谱测量仪器是美国ASD公司开发生产的FieldSpec3便携式光谱仪，其光谱范围为350～2 500 nm，采样间隔为1.4 nm([350，1 000 nm))和2 nm([1 000，2 500 nm])，重采样间隔为1 nm。光谱测量在暗室内进行，室内几何测试条件及测量过程的描述参见文献[11]。每个土样采集5条光谱曲线，进行拼接校正后，取其平均曲线，并去除噪声较大的350～399 nm和2 451～2 500 nm边缘波段。为扩大样本之间的光谱特征差异，对光谱曲线进行一阶微分变换。

2 估测模型建立方法

2.1 基于小波变换的光谱预处理

小波变换是基于傅里叶变换发展起来的数据处理方法,其通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析[12]。小波变换分为连续小波变换和离散小波变换，后者是前者的离散化，在实际运用中，考虑到连续小波变换计算量大、系数冗余度高，常常使用离散小波变换[4]。离散小波变换生成的每一层系数的数目随着分解层数的增加而减少，下层数目约为上层数目的1/2，但足以表示光谱的整体特征，且数据冗余相对较小。土壤光谱经离散小波变换处理后，可获取低频系数和高频系数。低频系数反映原始光谱明显的吸收特征，决定整个光谱的形状，高频系数反映原始光谱的噪声及微小的吸收特征[13]，通过离散小波变换舍去小波高频系数，提取小波低频系数，能够一定程度上减少由光谱仪测试条件等不确定因素造成的高频噪音[14]。在使用小波变换时，首先要选择合适的小波基，常用的小波基有Haar，Daubechies，Biorthogonal和Symlet等，陈红艳等[14]和栾福明等[15]都曾对上述4种小波基的表现进行研究，结果表明，基于Bior1.3小波基进行建模的精度最高。因此，本文采用Bior1.3小波基对土壤反射率的一阶导数光谱进行多层离散小波变换，提取各层的小波低频系数作为SPA算法的输入变量。研究发现，随着分解层数的增加，小波低频系数与原始光谱相关性逐渐降低，根据前人研究经验，本文选取1～7层小波低频系数用于估测模型的建立。

2.2 基于SPA算法的变量选择

SPA算法利用向量的投影分析，寻找含有最低限度冗余信息的变量组合，并使变量之间的共线性达到最小，同时大大减少建模所用的变量个数，以提高建模速度。有关SPA算法运算步骤详见文献[16]。

利用SPA算法分别对土壤全谱和1～7层的小波低频系数进行变量筛选，图2为土壤全谱和各分解层经SPA算法筛选得到的变量的分布情况。从图2中可以看出，入选的变量中，在近红外范围的居多，可见光的较少，这是由于有机质主要源于农作物遗体，由糖类化合物、纤维素、半纤维素、含氮化合物等组成，这些成分中的C-H键、C-O键、N-O键、N-H键等的光谱响应区域位于近红外区域[6]。

(a)土壤全谱 (b)第1层小波系数 (c)第2层小波系数 (d)第3层小波系数

2.3 模型建立

为验证小波变换和SPA算法的结合在黑土有机质含量高光谱估测上的有效性，本文分别基于土壤全谱、1～7层小波低频系数、SPA算法选择的变量，利用PLS和SVM两种方法建立估测模型。

PLS是多元定量分析中一种常用的方法，被广泛应用于近红外、红外、拉曼等波谱定量分析模型的建立，已成为光谱分析中建立线性定量校正模型的通用方法。PLS将数据压缩与回归结合起来，通过依次选择正交因子来扩大因变量与自变量之间的协方差[17]。

SVM作为一种非线性建模方法，在土壤参数估测中得到广泛应用，并取得了不错的效果。SVM通过非线性映射将输入向量映射到高维特征空间，然后在这个特征空间中求解凸优化问题[18]，但是这样就增加了运算的复杂度，而核函数的使用可以很好地解决这个问题，本文选择应用较为普遍、建模效果较好的径向基函数作为SVM的核函数。采用径向基函数时，内核参数和容错惩罚系数是2个必要调整参数，其取值直接影响模型精度，本文采用训练集交叉验证和网格搜索法进行参数寻优。

2.4 模型验证

采用决定系数R2和均方根误差(root mean square error,RMSE)对估测模型进行评价，其计算公式分别为：

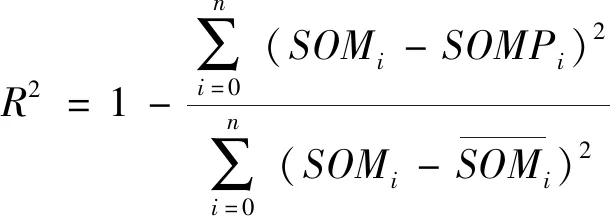
(1)

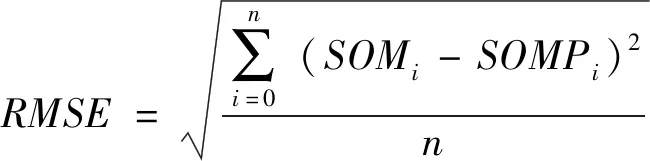
(2)

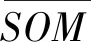
3 实验结果及分析

分别基于土壤全谱和1～7层小波低频系数，采用PLS方法和SVM方法构建黑土有机质含量估测模型，并利用验证样本集进行模型评价，得到的决定系数R2和均方根误差RMSE如表2所示。从表2可以看出，经小波变换处理后，模型精度确实得到了一定程度的提高：采用PLS方法时，R2由土壤全谱的0.79提高至第5层的0.88，RMSE由土壤全谱的6.06 g·kg-1降低至第5层的4.56 g·kg-1；采用SVM方法时，R2由土壤全谱的0.75提高至第5层的0.87，RMSE由土壤全谱的7.46 g·kg-1降低至第5层的4.96 g·kg-1。从表2中同时也可以发现，1～7层小波低频系数中，仅第4，5，6层的模型精度高于土壤全谱，而第1，2，3，7层的模型精度低于土壤全谱精度，可见，经小波变换处理后，并非每一层的精度都高于原始光谱，整体上是先升高再降低的趋势，中间层的模型精度最高，这一规律与王延仓等[6]的研究结论一致，产生这一现象的主要原因是由于有机质组成成分复杂多样，各成分均有不同的光谱响应范围，如果光谱分辨率较高则不能充分利用有机质各成分的光谱信息，而光谱分辨率较低则降低信噪比，进而对建模产生负面影响。

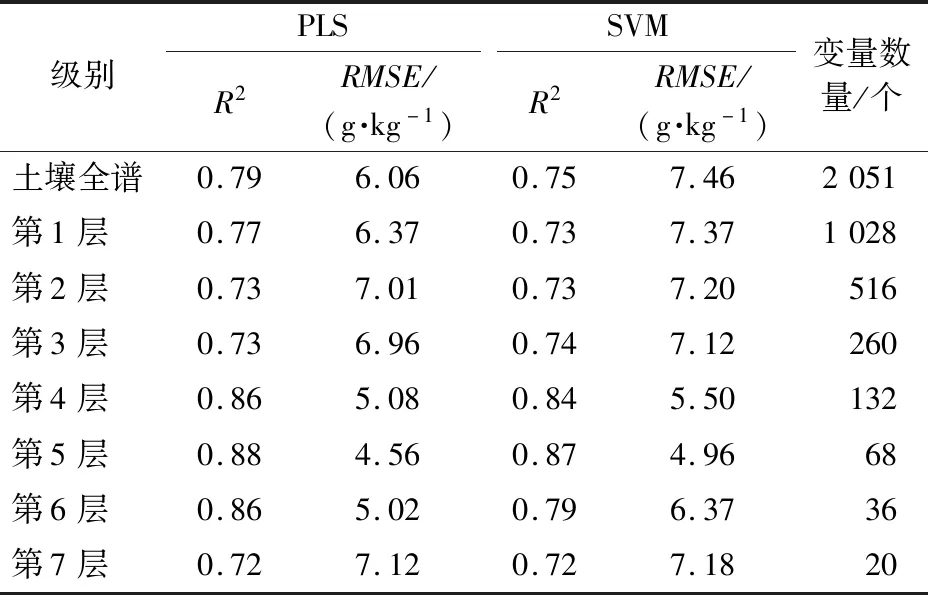
表2 土壤全谱和1～7层小波低频系数的估测模型评价结果Tab.2 Evaluation results of the estimation models of soil original spectrum and the wavelet coefficients of 1 to 7 levels

分别基于经SPA算法筛选获得的土壤全谱和第1～7层小波低频系数变量，采用PLS方法和SVM方法构建黑土有机质含量估测模型，并利用验证样本集进行模型评价，得到的决定系数R2和均方根误差RMSE如表3所示。对比表2和表3可以看出，经SPA算法处理后，不仅变量数目得到了大幅降低，而且模型精度也得到了一定程度的提高：采用PLS方法时，R2由0.88提高至0.93，RMSE由4.56 g·kg-1降低至3.48 g·kg-1；采用SVM方法时，R2由0.87提高至0.91，RMSE由4.96 g·kg-1降低至4.12 g·kg-1。另外，对比表2和表3可以发现，对于PLS方法，经SPA算法处理后，第2～7层小波低频系数的模型精度得到了提高，而土壤全谱和第1层小波低频系数的模型精度反而降低；对于SVM方法，经SPA算法处理后，土壤全谱和第1～4层小波低频系数的模型精度得到了提高，而第5～7层小波低频系数的模型精度则变换不大。可见，若不经小波变换处理，仅采用SPA算法，模型精度并不一定能够提高，此结论进一步验证了小波变换和SPA算法的结合在黑土有机质含量高光谱估测上的有效性。

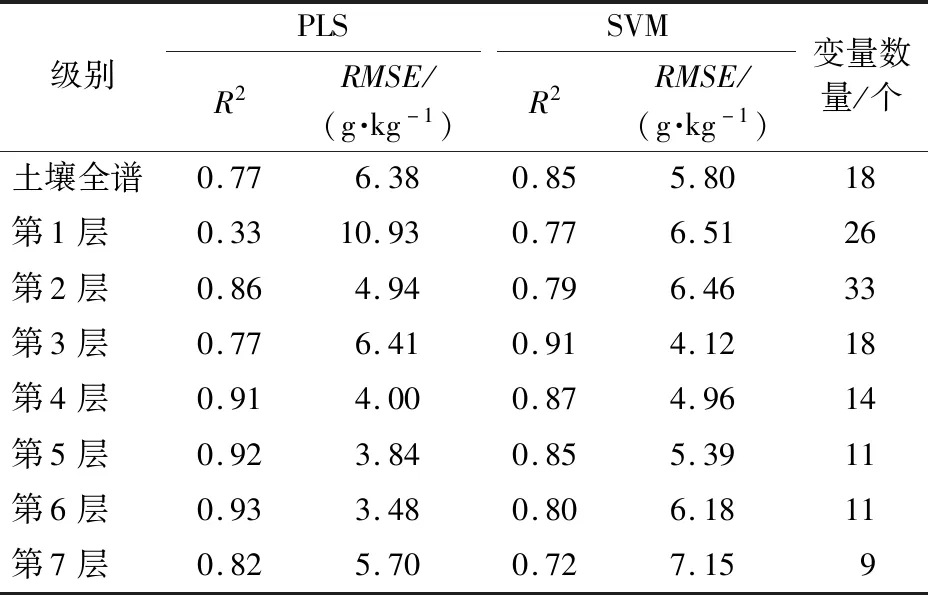
表3 SPA算法筛选后的土壤全谱和1～7层小波低频系数的估测模型评价结果Tab.3 Evaluation results of the estimation models of the soil original spectrum and the wavelet coefficients of 1 to 7 levels screened by successive projections algorithm

通过对比表2和表3中使用PLS和SVM方法获得的模型精度发现，PLS精度整体上高于SVM。采用PLS方法时，最优模型的决定系数R2和均方根误差RMSE分别为0.93和3.48 g·kg-1，采用SVM方法时，最优模型的决定系数R2和均方根误差RMSE分别为0.91和4.12 g·kg-1。

分别将基于土壤全谱、基于小波变换的最优模型、基于小波变换和SPA算法的最优模型获得的验证样本有机质预测值与实测值进行对比，图3为预测值与实测值的散点图，散点离直线越近表示预测效果越好。从图中可以看出，6个模型都没有欠拟合和过拟合现象发生，其中基于小波变换、SPA算法和PLS建立的模型预测结果最好；而未经小波变换和SPA算法处理，仅采用SVM建模的预测结果最差。

(a)基于土壤全谱的模型(PLS) (b)基于小波变换的最优模型(PLS) (c)基于小波变换和SPA的最优模型(PLS)

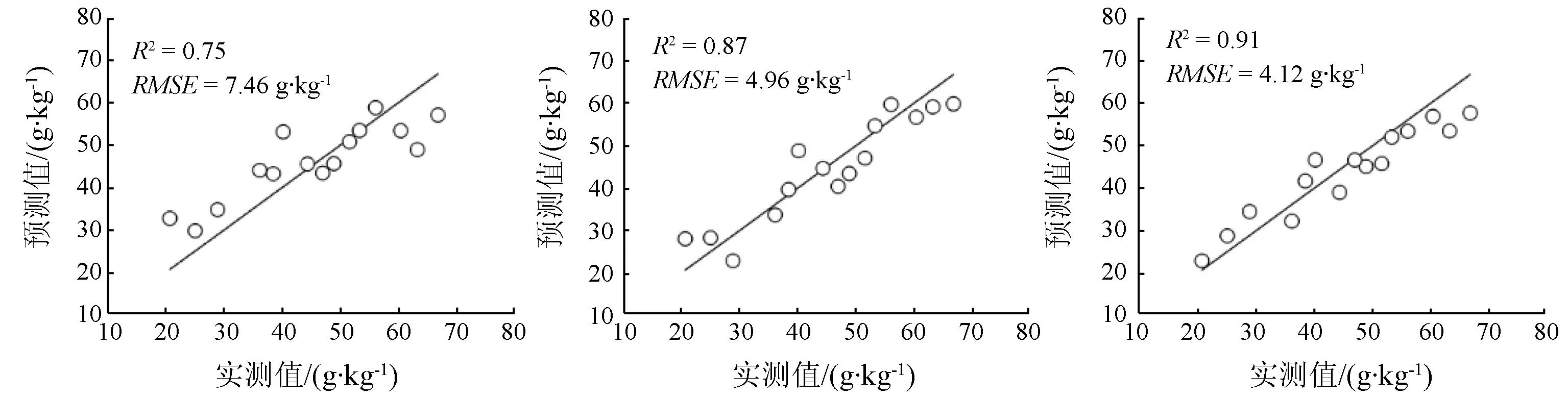
(d)基于土壤全谱的模型(SVM) (e)基于小波变换的 最优模型(SVM) (f)基于小波变换和SPA的最优模型(SVM)

4 结论

本文在黑土有机质含量高光谱估测中引入了小波变换和SPA算法，为验证小波变换和SPA算法的结合在黑土有机质含量高光谱估测上的有效性，分别基于土壤全谱、1～7层小波低频系数、SPA算法选择的变量，利用PLS和SVM两种方法建立了估测模型，主要结论如下：

1)经小波变换处理后，模型精度确实得到了提高，采用PLS方法时，R2由土壤全谱的0.79提高至第5层小波低频系数的0.88，RMSE由6.06 g·kg-1降低至4.56 g·kg-1；采用SVM方法时，R2由土壤全谱的0.75提高至第5层小波低频系数的0.87，RMSE由7.46 g·kg-1降低至4.96 g·kg-1。

2)经小波变换和SPA算法处理后，不仅变量数目得到了大幅降低，而且模型精度也得到了提高，采用PLS方法时，R2由土壤全谱的0.79提高至第6层小波低频系数的0.93，RMSE由6.06 g·kg-1降低至3.48 g·kg-1；采用SVM方法时，R2由土壤全谱的0.75提高至第3层小波低频系数的0.91，RMSE由7.46 g·kg-1降低至4.12 g·kg-1。

3)对于1～7层小波低频系数，整体上是先升高再降低的趋势。未使用SPA算法时，PLS和SVM均是第5层模型精度最高，R2分别为0.88和0.87，RMSE分别为4.56 g·kg-1和4.96 g·kg-1。使用SPA算法后，PLS第6层模型精度最高，SVM第3层精度最高，二者的R2分别为0.93和0.91，RMSE分别为3.48 g·kg-1和4.12 g·kg-1。

4)PLS和SVM相比，PLS精度整体上高于SVM。采用PLS方法时，最优模型的决定系数R2和均方根误差RMSE分别为0.93和3.48 g·kg-1，采用SVM方法时，最优模型的决定系数R2和均方根误差RMSE分别为0.91和4.12 g·kg-1。

迄今为止，许多土壤有机质含量高光谱估测研究中都采用了小波变换或SPA算法，并都取得了较好的估测效果，但将二者结合起来用于有机质含量高光谱估测的研究还非常有限，本研究结果表明结合小波变换和SPA算法进行黑土有机质含量高光谱估测是可行的，相比于使用单一算法，二者的结合能够获得更高的模型精度。但本文在建模过程中仅采用Bior1.3小波基进行小波变换，而事实上小波基种类很多，选用不同的小波基势必得到不同的建模精度，因此，未来将会在土壤有机质含量高光谱估测中针对小波基进行系统研究。