低开关频率的五相永磁同步电机有限集模型预测电流控制算法

张 靖， 武雪松， 李婷婷， 余 彬， 宋文胜

(1. 成都运达科技股份有限公司， 四川 成都 611756； 2. 西南交通大学电气工程学院， 四川 成都 611756)

1 引言

与传统的三相电机驱动系统相比，多相永磁同步电机(Permanent Magnet Synchronous Machine，PMSM)系统具有以下优点：①功率密度高、可靠性强，在一相或多相出现故障时可以容错运行[1-4]；②逆变器容量大，适用于低压大功率的应用场合；③电机的机械噪音较小，输出转矩的脉动幅值明显减小。目前，多相电机驱动系统在航空航天、船舶推进等领域中已经得到了广泛的推广与应用。

在多相电机控制算法方面，许多学者研究了适用于多相系统的矢量控制[5]与直接转矩控制(Direct Torque Control, DTC)算法[6，7]，并获得了良好的控制效果。近年来，在对高性能控制算法的持续探索中，模型预测控制(Model Predictive Control, MPC)算法引起了人们广泛的关注。其中，有限控制集模型预测控制算法(Finite Control Set Model Predictive Control, FCS-MPC)易于将变换器的离散特性与控制目标相结合，属于应用较多的MPC算法[8-11]。根据控制目标的不同，MPC算法又可分为模型预测电流控制、模型预测转矩控制[12]、模型预测功率控制[13，14]等。

在FCS-MPC算法中，每一个控制周期内需要根据预测模型对控制集中的所有元素进行预测计算，再结合参考值与预测值判断电压矢量的作用效果，选出评价函数值最小的电压矢量作为最优电压矢量。文献[15]中，作者以五相感应电机为研究对象，验证了FCS-MPC算法在多相电机控制中的可行性，并对比分析了FCS-MPC算法与传统PI-PWM控制算法的差异。此外，文献[15]通过实验法研究了权重系数对控制性能的影响，并分析了控制集的元素个数对控制效果与计算量的影响，实验结果表明，使用21个电压矢量能在减小计算量的前提下取得较好的电流控制效果。

在中高压电机驱动系统中，为了降低开关损耗并防止开关器件过热，通常需要在控制算法中引入对开关频率的限制。文献[16]中以大功率三相异步电机为对象，首先提出了一种基于模型预测的DTC算法，该算法通过将转矩与磁链限制在给定环宽范围内减小开关的切换次数；文献[17]通过实验研究了低开关频率的MPC-DTC算法与传统DTC算法在性能上的差异，实验结果表明低开关频率的MPC-DTC算法在全速域范围内都有着更好的性能。通过借鉴文献[16]与文献[17]中的控制思想，文献[18]提出了一种基于斜率控制的低开关频率算法。该控制算法中省去了外推计算环节，直接从待选电压矢量中选取斜率最小的电压矢量作为最优电压矢量。

目前鲜有针对五相系统低开关频率FCS-MPCC算法的研究报道。因此，本文结合五相系统的自身特点，提出了一种适用于五相PMSM的低开关频率FCS-MPCC算法。首先，结合电流预测值对控制集中的元素进行初步筛选，选出能满足电流控制需求的有效电压矢量；然后，利用电流采样值与预测值进行线性外推计算，结合设定的区域边界判断电流的轨迹；接着，重新设计了评价函数，在评价函数中体现出对开关频率的限制。最后，本文在小功率样机上对所提算法进行了实验验证与对比分析。

2 系统结构模型和传统FCS-MPCC

2.1 五相两电平逆变器

图1给出了五相两电平电压源逆变器-电机系统的电路结构，其中Vdc代表直流侧电压值。

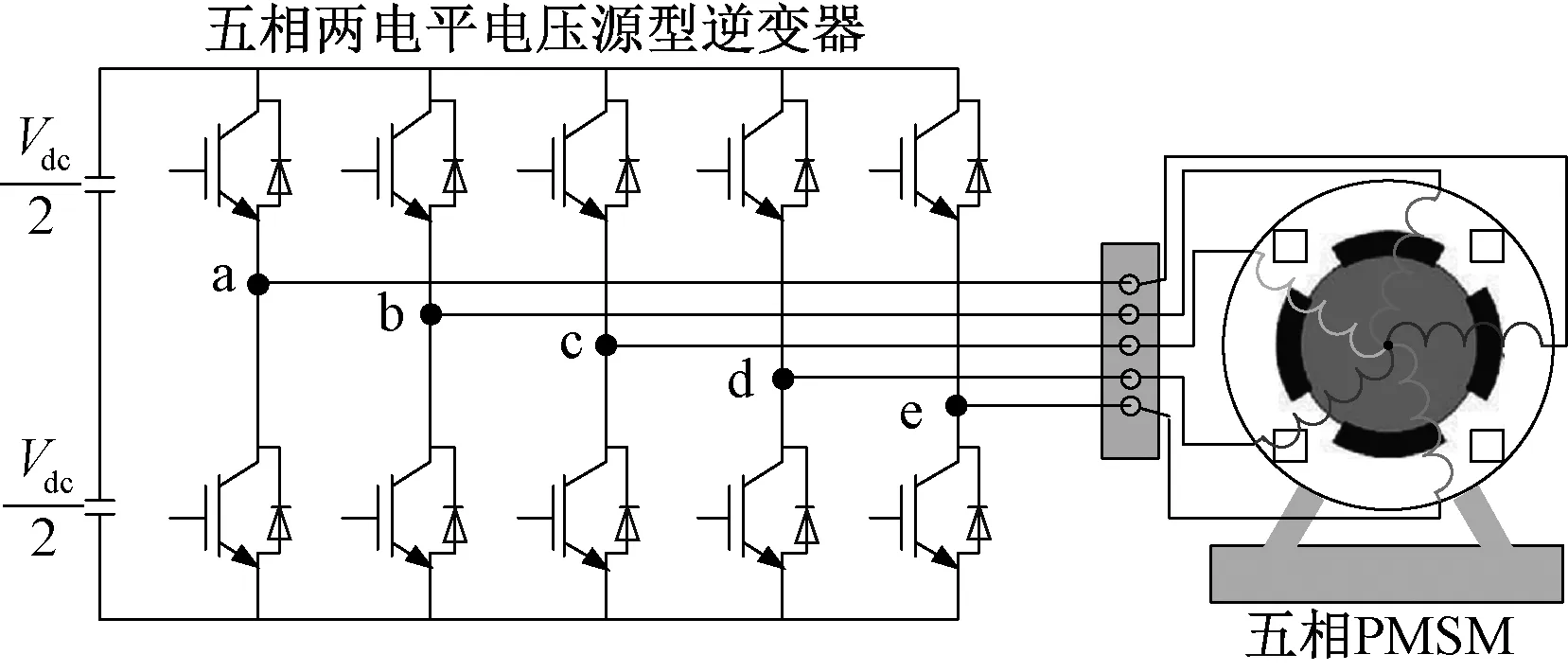
图1 五相电压源逆变器-电机简化结构图

五相两电平逆变器中，每个桥臂都可以输出两种开关状态，因此五相逆变器一共可以产生32个开关状态，对应30个有效电压矢量和2个零电压矢量。五相系统中，谐波子空间的存在使电压矢量在α1-β1与α3-β3子空间中均会产生映射。图2给出了30个有效电压矢量(不包含零矢量)在α1-β1子空间与α3-β3子空间中的分布。

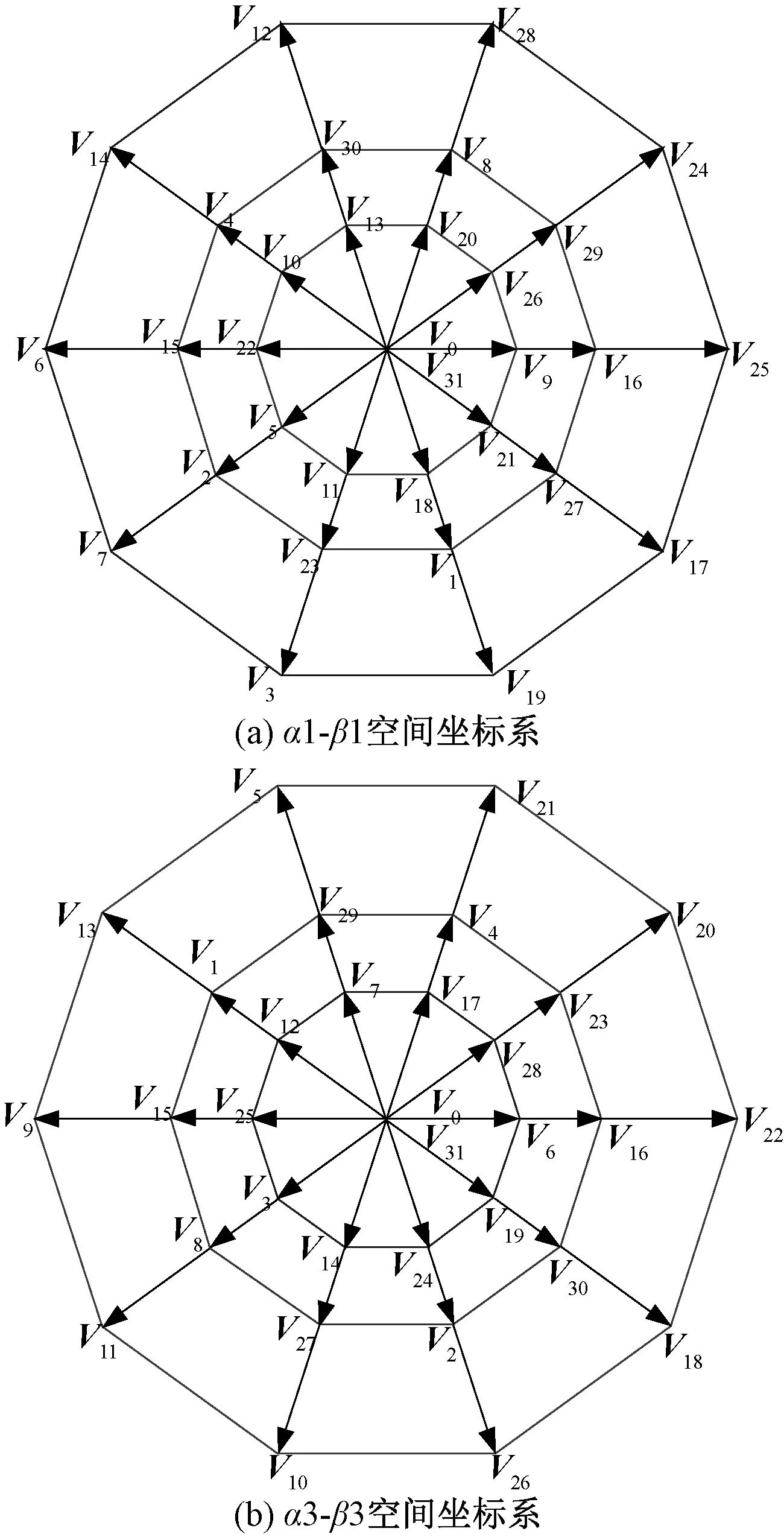
图2 五相逆变器空间电压矢量分布

在每个子空间中，30个有效电压矢量均匀分布10个方向上，每个方向上都包含3个幅值不同的电压矢量。为了方便表达，定义电压矢量为Vi=(SaSbScSdSe)，其中“S=1”表示此相桥臂的上管导通，“S=0”表示此桥臂的上管关断。根据电压矢量在α1-β1空间中的幅值，32个电压矢量可以分为L、M、S和Zero组，如表1所示。

表1 电压矢量分组

由图2可知，L组电压矢量在基波空间中处于最外层，而在谐波空间中对应最内层电压矢量。基波空间中的最内层电压矢量映射到谐波空间中后成为最外层电压矢量。M组电压矢量在两个子空间中具有相同的幅值。此外，同一个电压矢量在基波空间与谐波空间中的相位也不相同。

2.2 五相PMSM数学模型

通过坐标变换，可以得到五相PMSM在旋转坐标系d1-q1与d3-q3下的状态方程，如式(1)所示。

(1)

为了便于分析，本文忽略了涡流效应与定子表面齿槽带来的影响，并认为永磁体只产生正弦分布的磁势。式中，id1、iq1、id3、iq3分别为电机定子电流在d1-q1与d3-q3子空间中的分量；Vd1、Vq1、Vd3、Vq3分别为逆变器输出的电压在d1-q1与d3-q3子空间中的分量；Rs为电机定子电阻；Ld与Lq分别为d轴电抗与q轴电抗；Lls为绕组漏感；ωe为电机的电角速度，ψf为永磁体的磁链幅值。

2.3 传统FCS-MPCC算法

由于机械量的变化相对较慢，在一个很短的时间间隔内，可以认为电机的转速为一个定值。对式(1)中的电机模型进行前向欧拉离散化，可以得到五相PMSM的预测模型，其中Ts代表控制周期：

(2)

其中

(3)

(4)

(5)

由式(2)可知，根据电流在k时刻的采样值、电机的转速以及施加的电压矢量，结合预测模型可以得到电流在k+1时刻的预测值。施加的电压矢量会直接影响电流的预测值。

在FCS-MPCC算法中，控制集中的每一个电压矢量都对应一组电流预测值，因此需要通过评价函数选出最优的电压矢量。评价函数用来量化电流预测值与电流给定值之间的偏差大小，其具体形式为：

(6)

式中，Wxy为权重系数；Imax为电流保护项。电流保护项用于防止过大的电流对系统造成损害，其定义如下：

(7)

(8)

当电流预测值没有超出最大电流的限制时，Imax的值为零，因此对评价函数没有影响；当电流的预测值过大时，Imax为一个足够大的值，因此对应的矢量将不会被选取。评价函数描述了电流预测值与给定值之间的偏差，评价函数的值越小则表示电流预测值与给定值的偏差越小，评价函数值最小的电压矢量即为最优电压矢量。

传统FCS-MPCC算法在每个控制周期内的具体实施步骤为：

(1) 采样第k时刻的定子电流、电机转速等基本信息。

(2) 根据电流预测模型，对控制集中的所有电压矢量进行遍历计算，预测出在该电压矢量作用下电流在第k+1时刻的值。

(3) 针对每一组预测结果，根据电流预测值与电流参考值计算得到评价函数的值。

(4) 对评价函数值进行排序，选取评价函数最小的电压矢量施加给逆变器。

3 降低开关频率的FCS-MPC算法

3.1 有效电压矢量的筛选

在降低开关频率的FCS-MPCC算法中，首先根据预测电流的值对控制集中的电压矢量进行初步筛选，得到有效电压矢量。以电流id1为例，图3给出了有效电压矢量的判断依据。

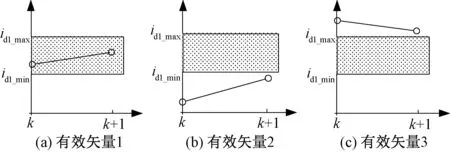
图3 有效电压矢量的判断依据

图3中给出了三种选取有效电压矢量的情况，其中阴影部分表示电流id1的给定范围，带圆圈的线条表示电流在该电压矢量作用下的变化轨迹。

(1) 如图3(a)所示，若电流id1(k+1)位于给定范围之内，则对应的电压矢量属于有效电压矢量；此外，即使id1(k)不在给定范围内，只要id1(k+1)位于设定的给定范围中，该电压矢量同样可以被认为是有效电压矢量。

(2) 电流id1(k)与电流id1(k+1)虽然都不在给定范围之中，但有着向给定区域靠近的趋势，如图3 (b)与图3 (c)所示。在这种情况下，对应的电压矢量同样可以被认为是有效电压矢量。

在五相系统中，控制变量包括基波电流与谐波电流，因此在筛选有效电压矢量时需要分别对id1、iq1与id3、iq3进行判断。为了简化算法，可以将谐波电流id3、iq3合并为一项：

(9)

对于控制集中的每个电压矢量，只有当id1、iq1与id3-q3能同时满足限制时，此电压矢量才能被称为有效电压矢量。

传统FCS-MPCC算法中，d-q轴电流纹波与控制频率直接相关，且电流的波动范围难以直接确定。在本文所提算法中，电流的给定值是一个区域，便于实现对电流控制精度的控制。

3.2 线性外推计算

在传统FCS-MPC算法中，电流的给定是一个具体的数值。而考虑了开关频率的限制以后，电流的给定扩大到一个区域范围。如图4所示，以电流id1为例，阴影部分表示电流的给定范围，η为偏差范围的宽度。

图4 电流预测与线性外推

假设第k时刻作用在逆变器上的电压矢量为Va(11001)，图4中分别给出了电流id1(k)在Vb(10001)、Vc(10000)、Vd(00011)和Ve(00111)作用下的变化轨迹。根据2.1节中的筛选依据，电压矢量Vb与Ve无法满足电流控制性能的要求，只有Vc与Vd是有效电压矢量。

为了描述电流轨迹的变化趋势以及电流在给定范围内的停留时间，可以根据电流的采样值与预测值进行线性外推，如图4中的虚线部分所示。N代表电流外推值到达给定区域边界的时刻，以电压矢量Vc与Vd为例，Vc对应的N值为1.5，Vd对应的N值为3.8。因此，在电压矢量Vd的作用下电流id1可以在给定区域内停留更长的时间，意味着在k+1之后的若干个控制周期内无需切换电压矢量，因此可以在一定程度上减小开关切换次数。

N值的计算方式如下：

(10)

(11)

3.3 评价函数设计

根据电流预测值与电流采样值，可以筛选出有效电压矢量；进一步地，利用线性外推原理可以得到该电压矢量对应的外推步长N。对电流轨迹进行线性外推是为了估算电流在给定区域内停留的时间：停留的时间越长则意味着更少的平均开关切换次数。在低开关频率的FCS-MPCC算法中，评价函数中应同时包含开关切换次数与电压矢量对应的外推步长N。对于第j个有效电压矢量，评价函数值的计算方式如下：

(12)

式中，mj为从当前作用的电压矢量切换到有效矢量j时发生的开关切换次数。评价函数采用两个变量相除的形式，因此不需要引入权重系数，从而简化了控制器的设计。

以图4中的有效电压矢量Vc与Vd为例，表2给出了评价函数的对比。

表2 评价函数cost1计算举例

评价函数的值由两部分决定，分子是需要切换的开关次数，分母部分是有效电压矢量对应的外推值。为了得到较低的平均开关频率，发生切换的开关应尽可能少，而对应的外推值则应尽可能大。因此，较小的评价函数值越小对应着较低的平均开关频率。在每个控制周期内，应选取评价函数值最小的有效电压矢量作为最优电压矢量施加给逆变器。

在每个控制周期中，首先需要筛选出有效矢量。然而，在某些暂态情况下，可能会出现有效矢量集为空集的情况。此时，应以电流的跟踪性能为首要目标，不再考虑对开关切换次数的限制，评价函数中仅包含电流误差项，采用式(6)中的评价函数进行计算。

需要指出的是，在所提算法中将电流控制在给定区域范围内是首要目标，对开关频率的降低是在保证电流控制性能的基础上进行的。

3.4 所提算法的实现

根据以上的分析过程，所提开关频率的FCS-MPC算法框图如图5所示，主要步骤如下所示：

图5 所提算法流程图

(1)测量电机在第k时刻的定子电流、转速等基本信息。

(2)对控制集中的所有电压矢量进行预测计算，获得该电压矢量作用下的电流预测值，然后进行有效电压矢量的筛选：若id1(k+1),iq1(k+1)以及id3-q3(k+1)同时满足判定条件，则该电压矢量属于有效电压矢量。

(3)检验有效电压矢量集是否为空集：若不是空集，针对选出的n个有效电压矢量，对第j(j=1,2，…，n)个有效电压矢量作用下的id1,iq1以及id3-q3分别进行线性外推，计算这三个被控量到达给定区域边界时的N值，并选取最小的值作为第j个电压矢量对应的Nj。根据当前时刻的开关状态计算切换到有效电压矢量j所需要的开关动作次数mj。

(4)评价函数计算。若存在有效电压矢量，根据式(12)计算每个有效电压矢量对应的评价函数值。若有效电压矢量集是空集，则根据式(6)计算对应的评价函数值。

(5)最优矢量的选取。对评价函数值进行排序，选取最小评价函数值对应的电压矢量作为最优矢量。

4 实验结果对比与分析

基于五相逆变器-永磁同步电机小功率实验平台，本文对所提算法进行了测试，图6给出了实验平台的主要结构。

图6 五相逆变器-永磁同步电机实验平台

五相PMSM与一台直流发电机同轴相连，直流发电机产生的电能在功率电阻上被消耗。电机的轴端接有旋转变压器，通过解码电路可以得到电机的转速以及转子位置角。实验中选用的控制器为TMS320F28335。PMSM的参数如表3所示。其中，q轴电流给定值由转速环PI控制器得到，各算法中采用相同的PI参数与控制周期。

表3 五相永磁同步电机参数

对于FCS-MPC算法，控制集中的电压矢量个数会直接影响控制效果。综合考虑计算量与控制性能后，本文使用21个电压矢量(10个大矢量、10个中间层矢量与1个零矢量)作为控制集。本文对比分析了传统FCS-MPCC算法(记作MPCC21)与所提算法(记作MPCC-LSF, Low Switching Frequency)在动态性能与稳态性能上的对比。

4.1 稳态性能对比

对比实验中，两种控制算法的控制周期均设置为150 μs，对应的控制频率大约为6.66 kHz。图7给出了MPCC-LSF算法在稳态时的转速、转矩以及电机相电流波形。其中逆变器直流侧的供电电压为80 V，电机的转速给定值为240 rad/s。

图7 稳态实验波形

在两种控制算法中，电机转速均能实现对给定值的有效跟踪，且定子电流正弦度良好。经实际测量，在此种工况下，MPCC21算法对应的开关频率为1.305 kHz，而MPCC-LSF算法中开关频率为1.11 kHz。相比于没有考虑开关频率限制的MPCC21算法，MPCC-LSF算法中开关频率减小了14.9%。

4.2 动态性能对比

图8是MPCC-LSF算法与MPCC21算在给定转速发生突变时的动态性能对比。

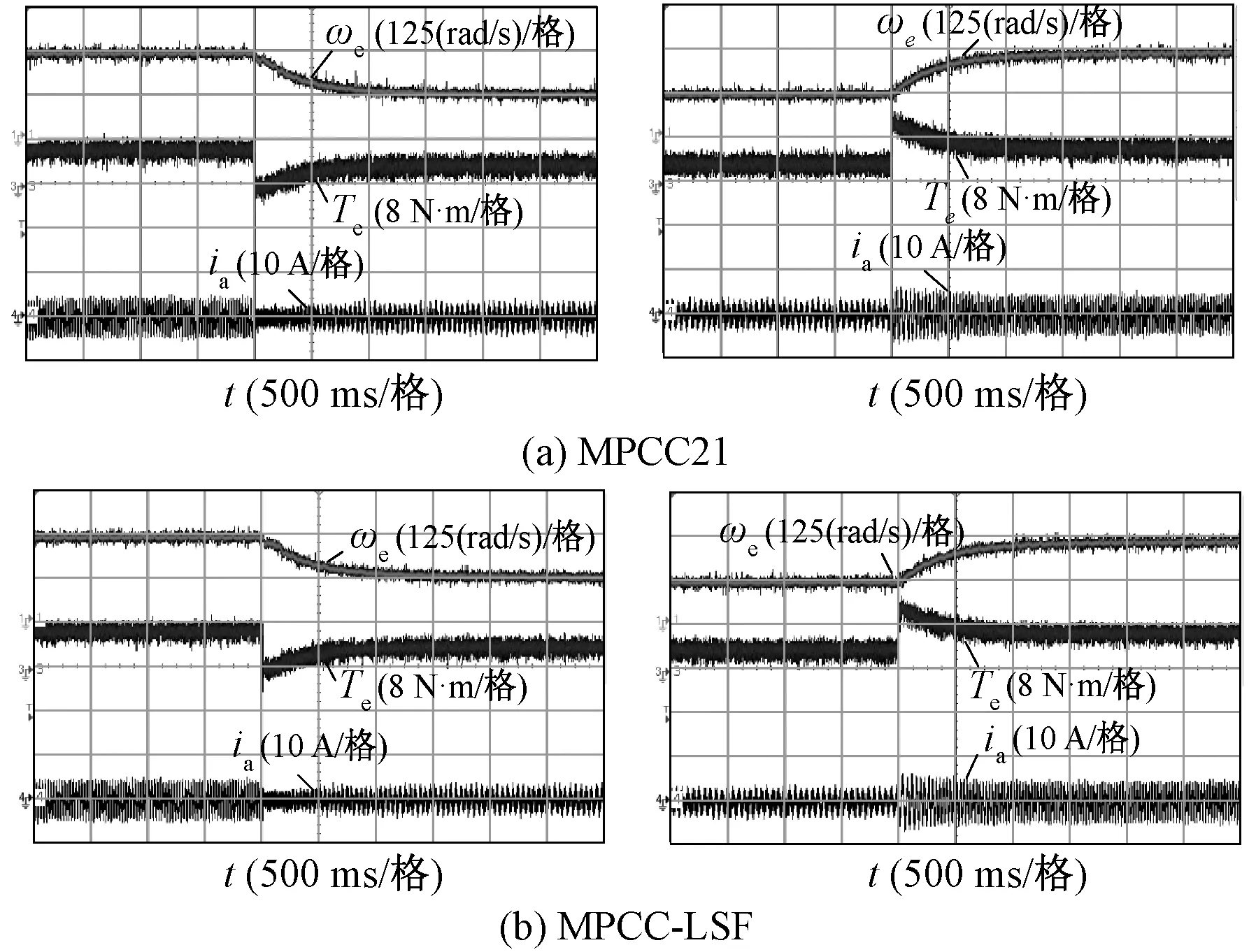
图8 给定转速突变实验波形

在转速突减实验中，给定转速由240 rad/s阶跃减小至120 rad/s，而转速突增实验中给定转速由120 rad/s阶跃增加至240 rad/s。对比图8(a)与图8(b)可知，MPCC-LSF与MPCC21均具有良好的动态响应能力。需要注意的是，作为负载的直流发电机的输出功率与转速有关，因此当转速发生改变以后，PMSM的输出转矩与定子电流幅值也会随之发生变化。

由实验结果可知，MPCC-LSF算法保留了传统算法动态响应迅速的优点。图9给出了MPCC-LSF算法在加速与减速过程中的d轴与q轴电流波形。

图9 MPCC-LSF在转速突变时的电流波形

在稳态与暂态过程中，所提算法始终保持着良好的电流控制精度。

4.3 开关频率对比

为了进一步验证MPCC-LSF算法在减小开关频率方面的效果，图10给出了MPCC-LSF算法与MPCC21算法在不同速度范围下的开关频率对比。

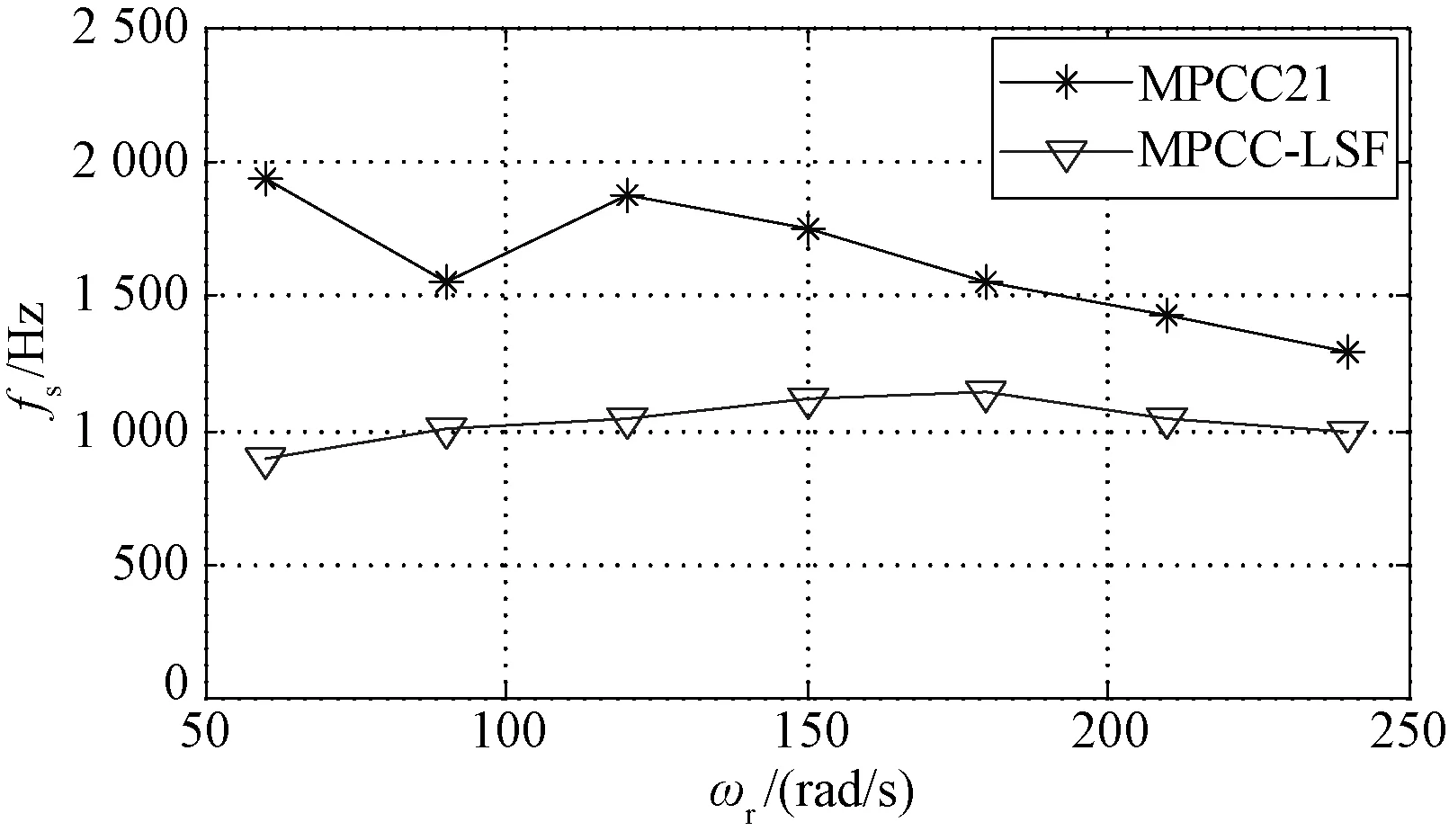
图10 不同转速下的开关频率对比

MPCC21算法的开关频率在1 kHz附近波动，在不同的电机转速下，MPCC-LSF算法都能够有效减小开关频率。需要说明的是，MPCC-LSF算法的实际开关频率与电机的工作点、控制周期的大小以及设定的电流环宽等都有关系。

5 结论

本文以五相PMSM为研究对象，针对大功率的应用场合，提出了一种能降低开关频率的MPCC算法。所提算法在预测计算之后增加了线性外推，并根据外推步长与开关切换次数重新设计了评价函数，在评价函数中体现出对开关频率的限制。实验结果证明，所提算进不仅保留了传统MPCC算法动态响应迅速的优点，还能在全速域范围内有效降低逆变器的开关频率。此外，所提算法同样适用于九相、十五相等多相电机驱动系统。