电动汽车负荷虚拟同步机参与电网频率调节的充放电策略与实现

李秉宇， 杜旭浩， 曾四鸣， 尹利科， 芮月晨， 肖国春

(1. 国网河北省电力有限公司电力科学研究院， 河北 石家庄 050021； 2. 河北拓朴建筑设计有限公司，河北 石家庄 050000；3. 西安交通大学电气工程学院， 陕西 西安 710048)

1 引言

近年来，由于清洁环保的优势，电动汽车(Electric Vehicles, EV)引起了广泛的关注。按照充电速度划分，EV有慢速充电和快速充电两种充电模式，且目前已有相关的EV 充电标准，例如SAE J1772[1]。慢速充电可以在不需要配电网大容量的情况下对EV 进行充电，但是通常需要6～8 h才能为完全耗尽的标准EV 电池充满电。因此，快速充电更被用户所青睐，仅需30 min即可从耗尽状态充电到电池容量的80%[2]。另一方面，EV连接到电网的随机性使电网的规划和运营变得困难。并且，相较于慢速充电，快速充电需要电网提供更大容量的功率，给电网的稳定运行带来了更多压力[3]。

虚拟同步机(Virtual Synchronous Machine，VSM)控制通过电力电子装置模拟同步电机，为电力系统提供惯量和阻尼支撑，是一种解决大量电力电子装置接入电力系统，造成稳定性问题的有效解决途径。VSM分为虚拟同步发电机(Virtual Synchronous Generator, VSG)和负荷虚拟同步机(Load-side Virtual Synchronous Machine, LVSM)。VSG主要应用于新能源发电中[4，5]，包括风电VSG和光伏VSG。LVSM包括采用VSM技术的各类用电设备，例如含整流器的EV充电桩、变频设备和电子产品等[6]。LVSM控制可以使整流器根据电网频率和电压实时调整负荷功率，实现网-荷动态平衡。

将LVSM策略应用于整流器的控制中，使EV与电网具有网-荷互动的功能，通过虚拟惯性和阻尼提高电网电压和频率的稳定性，可以减轻EV负荷对电网的影响。文献[7]提出了一种基于电流型负荷虚拟同步机的交流接口控制策略，对恒定电压(Constant Voltage, CV)充电模式下EV负荷增加的工况进行了分析，验证了虚拟惯性和阻尼可以实现柔性缓冲的功能，但缺少对恒定电流(Constant Current, CC)模式的分析，并且将EV负荷作为电阻负载进行分析，这与EV负荷的实际特性不符。基于LVSM的EV充放电方法，文献[8]中讨论了EV参与微电网的调频策略，本质上是根据微电网的频率对EV负荷充电功率指令进行调整，从而提升微电网的稳定性；文献[9]中提出了一种自主降额运行的LVSM控制方法，减轻LVSM接入对电网频率的影响，但考虑的是无穷大电网，并用LVSM的虚拟频率代替电网频率分析，这并不是一种与电网频率实时交互的控制策略；文献[10]中提出了一种根据电网频率调节PWM整流器直流侧电压的网荷互动方法，但通常直流母线电压是不变的，且直流母线电压频繁波动会引起母线储能电容器发热。

EV作为有源负荷，还可以提供EV入网(Vehicle to Grid, V2G)服务，通过EV电池储能改善电力系统的运行特性[11]。文献[12]提出了一种基于单级式EV充电拓扑实现V2G功能的控制结构，实现了电网和EV之间的双向功率流动；文献[13]将VSM技术运用到单相单级式家用EV电池充电器的控制中，以提供更高质量的V2G服务，但该技术在三相两级式公共EV电池充电站中的可行性还有待研究。

本文在电压控制型LVSM的基础上，提出了一种后级DC-DC电动汽车充电变流器与电网频率实时交互的电动汽车快速充放电控制策略和实现方法，在CC充电、CV充电和CC放电模式均能够根据电网频率的变化实时调整EV的充放电功率，有助于电网频率的恢复。而在LVSM虚拟惯性和阻尼的作用下，电网频率的变化率得到了有效衰减，电网频率的暂态和稳态稳定性均得到了提高。本文采用VSG模拟电网，通过本地负荷的变化影响电网频率，更加真实地反映了电网频率的变化过程。通过仿真，分析了采用本文所提控制策略前后电网频率随本地负荷变化的情况，验证了该策略和实现方法稳定电网频率的正确性和有效性。

2 电动汽车充放电控制策略

频率是衡量电能质量的一个重要指标，电力系统中频率的变化主要是由发电机损耗或负载增减引起的，而3%～5%的负载变化会对电力系统造成很大的干扰[14]。为研究电动汽车负荷接入对电网的影响，本文考虑用VSG模拟电网，通过本地负载的增减来影响电网频率，相比于直接设定电网频率降低的方式，能够更加真实反映电网频率的变化过程。

2.1 系统模型

图1 系统拓扑及控制结构

(1)

式中，Kω为一次调频系数；ωg为VSG的角频率；ω0为额定角频率，ω0=100π rad/s。

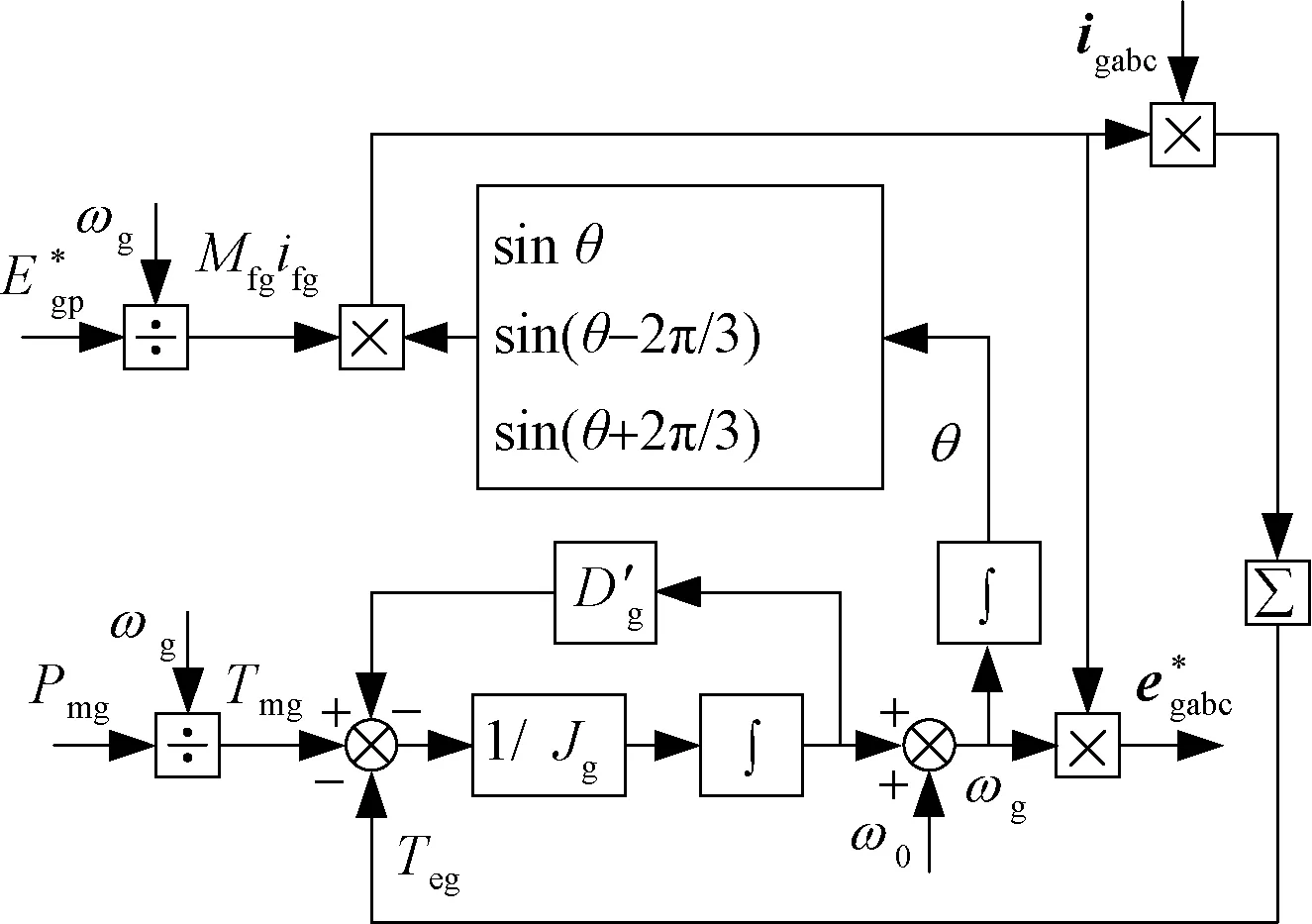
图2 VSG控制框图

图2的下半部分是对同步发电机转矩方程的模拟。

(2)

式中，Tmg为VSG输入的机械转矩；Teg为VSG输出的电磁转矩；Dg′为VSG的阻尼系数；Jg为VSG的转动惯量。

考虑到机械功率Pmg=ωgTmg，电磁功率Peg=ωgTeg，并将式(1)代入式(2)中，得到：

(3)

式中，Dg=Dg′ +Kω/ωg。式(3)表明电网一次调频系数Kω和阻尼系数Dg′可以合并为阻尼下垂系数Dg，考虑ωg≈ω0，有Dg≈Dg′ +Kω/ω0，即这两个环节在功能上相同，后续将采用Dg进行分析。

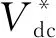
图3 LVSM控制框图

图3的下半部分是对同步电动机转矩方程的模拟。

(4)

式中，Te为LVSM输出的电磁功率；Tm为LVSM的机械功率指令；D为LVSM的阻尼系数；J为LVSM的转动惯量。

基于LVSM的AC-DC变流器控制用于提供恒定的直流母线电压，并使电动汽车负荷与电网在互动的过程中具备惯性和阻尼。

由于频率同步机制的存在，电网中的同步发电机电源和同步电动机负荷能够根据电网频率调节自身的功率：当电网频率升高，输出或消耗的有功功率减少；当电网频率降低，输出或消耗的有功功率增加。借鉴这一运行经验，基于LVSM控制的EV负荷在理论上也具有一定的需求侧响应能力。但由于直流母线电压控制回路的存在，当电网频率发生变化时，仅依靠前级AC-DC变流器控制无法实现充放电功率的动态调节。

图1中，后级DC-DC变流器基于双向Buck-Boost拓扑，用于实现EV充放电功率的控制和模式的切换，d为后级DC-DC变流器的占空比。在通常采用的CC/CV充电模式中，先通过CC模式充电至预定的电压，此时电池的荷电状态(State of Charge,SOC)达到80%左右；然后进入CV模式，逐渐减小充电电流直至电量充满[15]。整个充电过程中充电电流Ibat和电池电压Vbat的变化情况如图4所示，电池电压建立后，在很长一段时间内基本保持不变。

图4 CC/CV充电模式下的充电电流和电池电压

2.2 网荷互动的充放电策略

当电力系统中负荷功率增加导致发电机出力与负荷功率不平衡时，系统频率发生变化。虽然调速器具有一定的频率恢复功能，但当仅依靠一次调频的作用已不能使频率保持在正常工作区域内时，需要采取“低频减负荷”等措施维持系统安全稳定运行。

通过改变传统DC-DC变流器的控制方式，使EV负荷与电网之间建立互动机制，可以变传统的“切负荷”为实时的动态充放电功率调节，使电网频率具有一定的自愈功能。本文所提出的具有网荷互动功能的DC-DC变流器控制框图如图5所示。

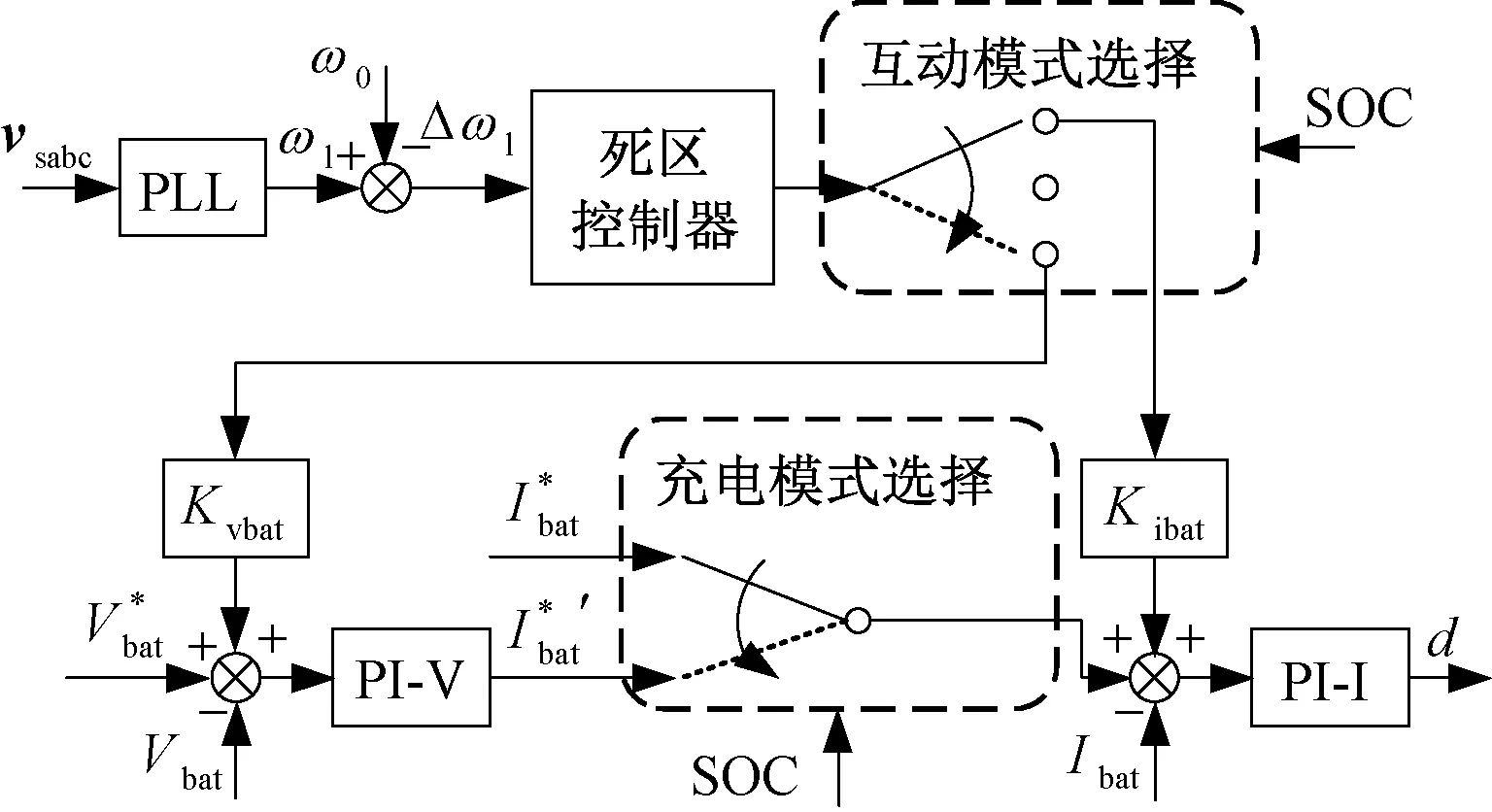
图5 DC-DC变流器控制框图

图5中，vsabc为采样到的三相本地负载电压，通过锁相环得到本地负载角频率ωl，ωl≈ωg，ωl与额定角频率ω0的差值Δωl为网荷互动所需的信息。死区控制器可以设置网荷互动的条件，当|Δωl|未超过允许的角频率变化量Δωl(max)时，互动模式选择模块中的开关与中间位置接通，EV负荷与电网之间没有互动，避免了电池充电状态的频繁变化，有助于延长电池寿命。

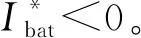
3 参数的选取和设计

互联系统的主要参数见表1。

表1 系统主要参数

3.1 模拟电网参数选取

设模拟电网容量Sg为100 kV·A，同步电机的惯性常数通常在2～10 s的范围内[16]，取VSG的惯性常数Hg=2 s。转动惯量与惯性常数的关系为：

(5)

由式(5)计算得到Jg=4.05 kg·m2。实际中，电网的转动惯量远大于LVSM的转动惯量。

阻尼下垂系数除了决定VSG的阻尼外，还会影响VSG在本地负载变化后频率的稳态工作点，通常根据100%的有功功率变化对应于n%电网频率的变化来设计。

(6)

参考输电网技术规范EN 50438，要求100%的有功功率变化对应于2%电网频率的变化[17]，由式(6)计算得到Dg=50.66 W·s2/rad2。

3.2 电池参数选取

根据SAE J1772，用于EV快速充电的接口通常有50 kW和100 kW两种功率等级，后级DC-DC电池充电变流器输出的直流电压范围在208～600 V[1]。本文选用50 kW的快充接口，额定充电电流Ibat(nom)=125 A。

准确的电池模型对于通过EV 充放电过程的分析至关重要，文献[18]中提出了用SOC、端电压、开路电压、内阻和放电电流来描述电池电化学行为的模型。模型参数通过放电曲线计算，并假定充电过程中参数相同。该电池模型计算数据与实际电池数据比较的结果表明，该模型具有90%的准确度。本文拟采用文献[18]中介绍的模型，电池参数见表2。

表2 电池参数

本文所采用的电池在额定放电电流下的放电曲线如图6所示。图6中包含指数区域、额定区域和建立区域。电池从完全放电的状态下开始充电时，首先CC充电至接近额定区域的末端(SOC≈80%)，然后进行CV充电，充电电流不断减小。

图6 电池恒流放电曲线

3.3 LVSM参数设计

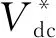
(7)

电网向LVSM传输的有功功率在直流侧被消耗，且与LVSM相比，DC-DC变流器的响应速度快得多，因此在LVSM控制下可以认为Ibat能够对指令值Ibat*进行实时跟踪，则LVSM消耗的有功功率Pe为：

(8)

根据双向功率传输原理[19]，由PCC流向LVSM的有功功率还可表示为：

(9)

式中，El为LVSM内电势有效值；Vs为本地负载电压有效值；滤波电抗Xs=ω0Ls。

对式(4)、式(7)～式(9)进行小信号分析，可得两级式电动汽车充电系统在本地负载频率扰动下的小信号模型，如图7所示。由图7可知，有功功率回路的环路增益为：

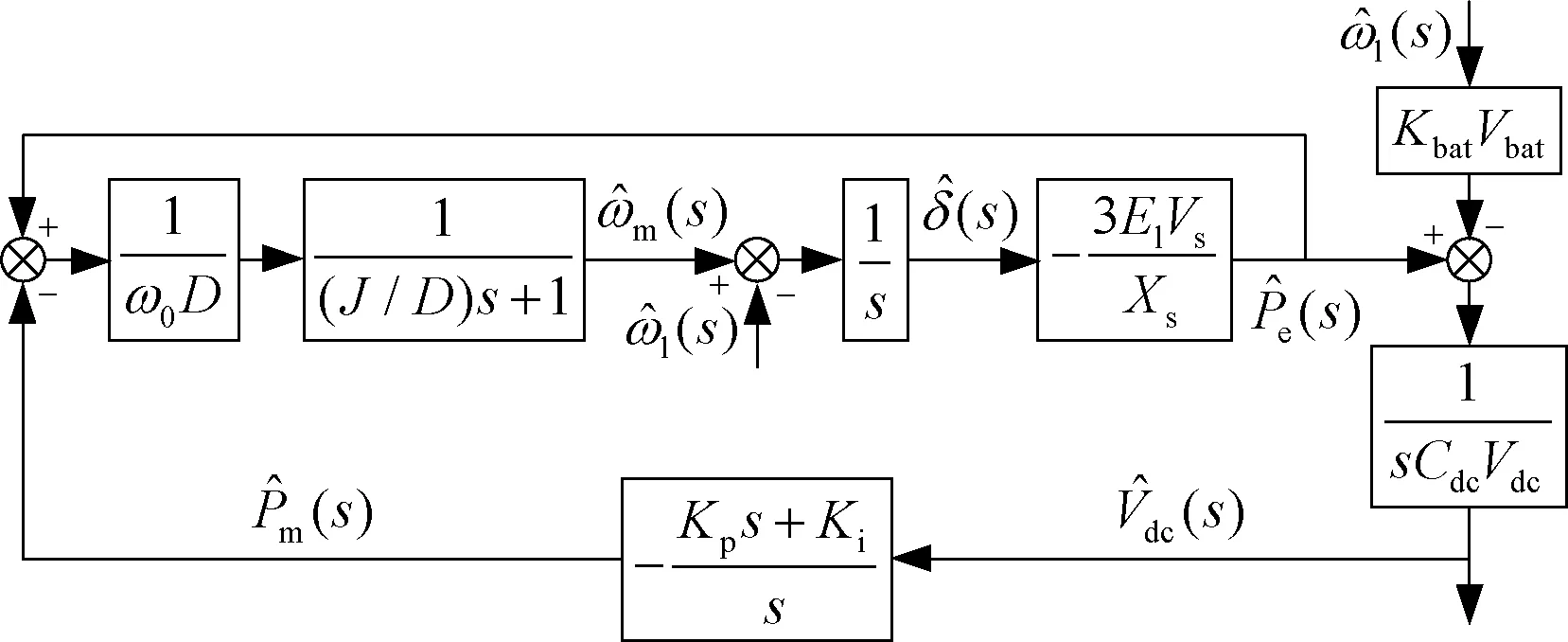
图7 充电系统在本地负载频率扰动下的模型

(10)

式中，ζp和ωpn分别为有功功率回路的阻尼比和自由振荡角频率。

式(10)与典型Ⅰ系统参数对应，且在有功功率回路的开环截止角频率ωpc处Tp(s)的幅值为1，因此：

(11)

通常设计ζp=0.707，即二阶系统最佳阻尼比。在选定ωpc后，即可得到J和D，完成有功功率回路的设计。文献[20]中指出，将ωpc设计在远小于2倍工频处，可以抑制瞬时有功功率脉动。当fpc=ωpc/(2π)=8.7 Hz时，由式(11)得到J=0.1 kg·m2、D=12 W·s2/rad2；当fpc=ωpc/(2π)=3.9 Hz时，得到J=0.5 kg·m2、D=27 W·s2/rad2。

由图7可知，直流侧电压回路环路增益为：

(12)

当J=0.1 kg·m2、D=12 W·s2/rad2时，取Kp=80 W/V、Ki=300 W/(V·s)，Tvdc(s)的频率特性如图8所示，开环截止频率fvdcc=ωvdcc/(2π)=1.9 Hz，相角裕度γ=61.1°，幅值裕度Gm=19.9 dB。将这组LVSM参数命名为参数1。

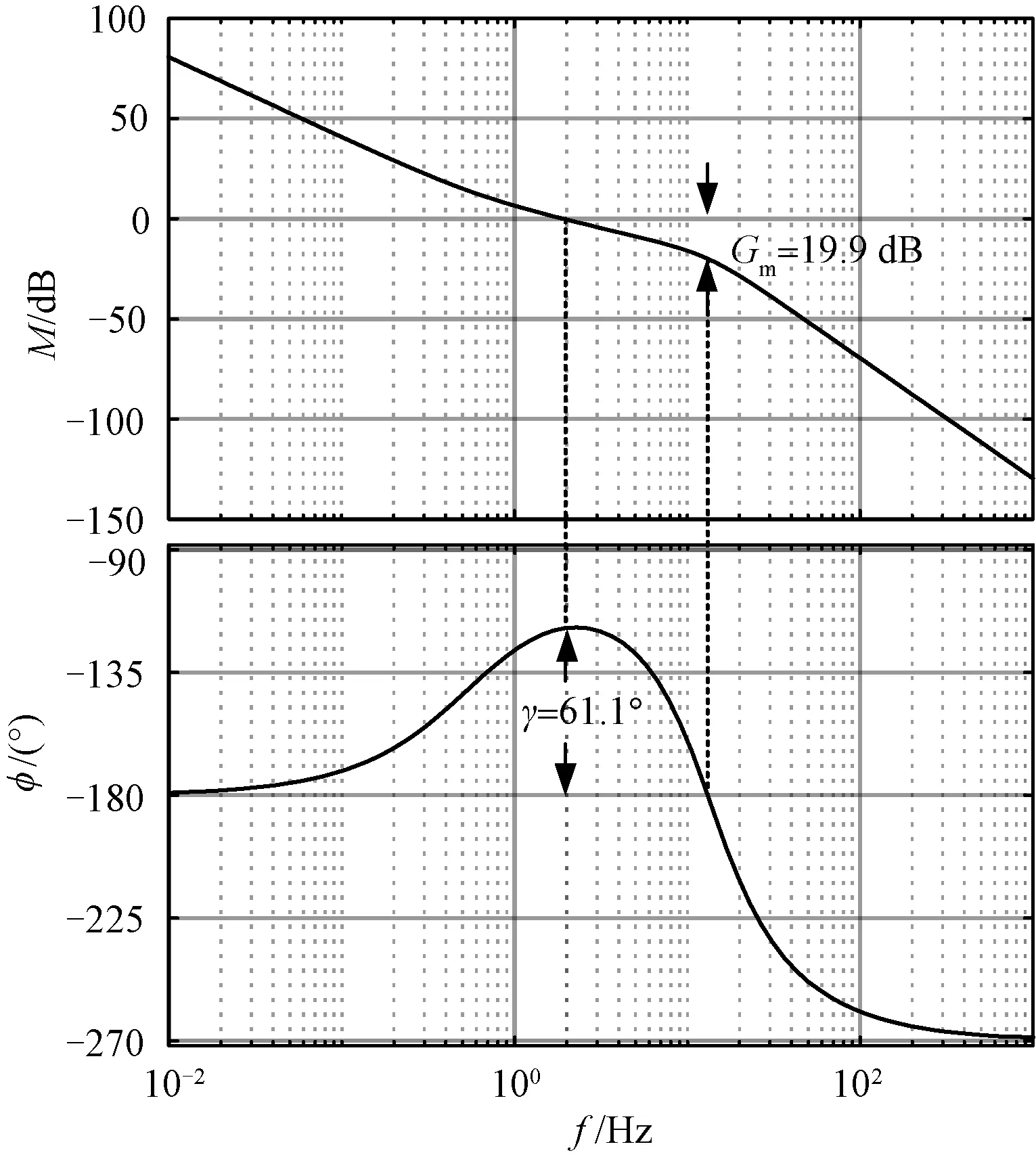
图8 LVSM直流侧电压回路的频率特性(参数1)

当J=0.5 kg·m2、D=27 W·s2/rad2时，为保证良好的控制性能，调整Kp=60 W/V、Ki=100 W/(V·s)，此时相角裕度γ=60.3°，幅值裕度Gm=15.4 dB。将这组LVSM参数命名为参数2。

3.4 DC-DC变流器网荷互动参数设计

CC充电时，充电电流调节系数Kibat反映了充电电流随电网频率变化的波动程度，若电网频率下降ni%时，LVSM不再从电网吸收有功，则Kibat为：

(13)

取ni=2，由式(13)得到Kibat=19.89 A·s/rad。

CV充电时，电池电压过高不利于系统的安全运行，电池电压过低会导致反向放电。因此，考虑CV充电模式下电池电压允许的变化范围为ΔVbat。设电网频率下降nv%时，LVSM电池电压达到最大允许跌落量，则Kvbat为：

(14)

取nv=2，ΔVbat=10 V，由式(14)计算得到Kvbat=1.59 V·s/rad。

根据电力系统正常运行的频率范围来确定死区控制器的阈值Δωl(max)，以华东电网为例，允许的频率波动范围为0.1 Hz[21]，因此设置Δωl(max)=0.63 rad/s。

4 仿真验证

当本地负载发生扰动时，电网频率相应发生变化，LVSM的虚拟惯量和阻尼承担起阻碍电网频率变化率(Rate of Change of Frequency, RoCoF)的作用，而DC-DC变流器的频率-电流/电压调节系数能够减小电网频率的变化量，二者共同对电网频率起到一定的支撑作用。直流母线电容作为能量的缓冲单元，其电压会因为本地负载的变化而波动。此外，CC模式的充放电电流和CV模式的充电电压也与电网频率息息相关。同时，本节还将讨论LVSM虚拟频率的变化过程及其与电网频率的关系。

4.1 CC充放电模式

首先验证所提出的控制策略在CC充电模式下对电网频率的影响。选择参数1，研究引入Ibat-ωl控制对系统动态过程和稳态工作点的影响；为了对比不同J的影响，对参数2的情形也进行了仿真。在t=0 s时，本地负载增加24%；在t=2 s时，感知到本地负载的增加后，电网有功功率指令相应地增加，使输入功率和输出功率相匹配，以模拟电网频率的恢复过程；在t=4 s时，本地负载减少24%；在t=6 s时，电网有功功率指令相应减少，使输入功率和输出功率相匹配，电网频率、LVSM频率、LVSM母线电压和充电电流的响应过程分别如图9(a)、图9(b)、图9(c)和图9(d)所示。

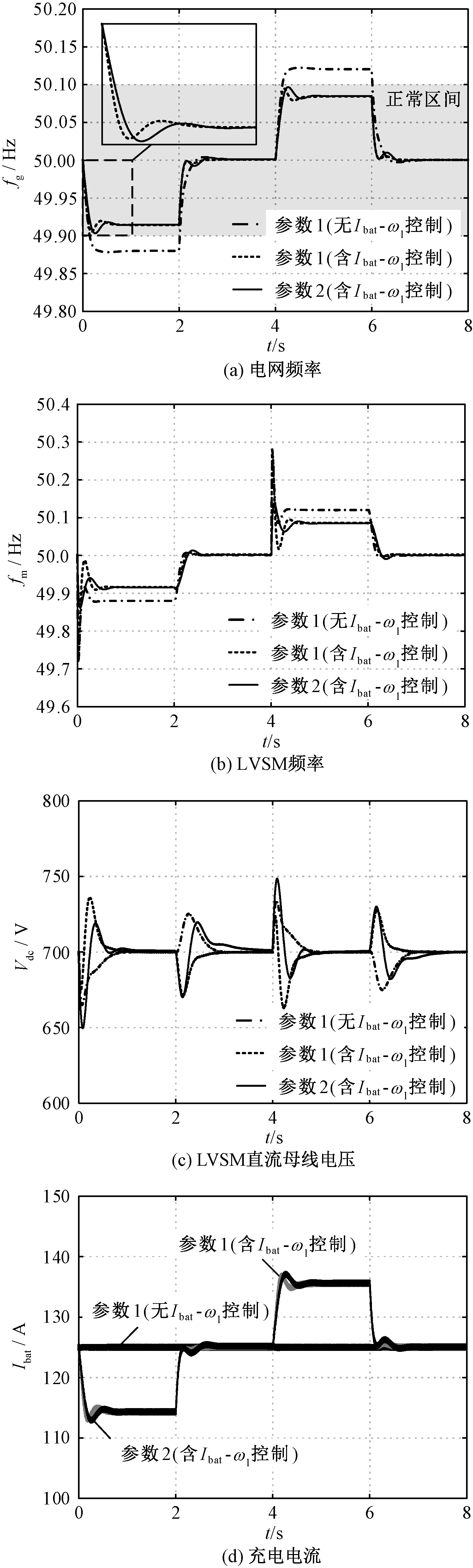
图9 CC充电模式下系统各变量的响应过程

对比图9(a)中是否含Ibat-ωl控制的曲线可知，引入Ibat-ωl控制后，电网频率的变化量减少。当发生由负载增减引起的电网频率变化，引入Ibat-ωl控制前Δfg=0.12 Hz，引入Ibat-ωl控制后Δfg=0.08 Hz，所提出的控制策略使电网维持在正常工作区域内，保障了电网频率的稳定性。

同时，如图9(b)中相应的两条曲线所示，在0.5 s前，电网频率和LVSM频率的动态变化过程存在较大差异。由于LVSM的转动惯量显著小于电网的转动惯量，在本地负载变化时刻附近LVSM频率的变化主要由其自身的小惯量特性决定。在0.5 s后，电网频率和LVSM频率完成同步。图9(c)中相应的两条曲线表明：引入Ibat-ωl控制前，本地负载的突增和突减引起了大约30 V的母线电压幅值跌落；引入Ibat-ωl控制后，本地负载的突增使直流母线电压幅值的跌落量减小，因为Ibat-ωl控制使LVSM动态减载，减弱了本地负载对直流母线电压的影响，但同时这种动态减载也造成了一定的反向升压；在大约1 s后，母线电压恢复到额定值。图9(d)中相应的两条曲线表明，电网频率变化使充电电流变化了约9%，没有出现电流的过冲。

对比图9(a)中两组不同参数下的曲线可知，选择较小的LVSM惯量(参数1)时，电网RoCoF=0.74 Hz/s；选择较大的LVSM惯量(参数2)时，电网RoCoF=0.53 Hz/s。LVSM更大的转动惯量使电网RoCoF更低，提升了电网频率的暂态稳定性。当RoCoF值超过上限(例如1 Hz/s)时，可能会导致保护继电器跳闸，对系统造成干扰[22]。

同时，如图9(b)中不同参数下的两条曲线所示，更大的转动惯量使LVSM的RoCoF更低，且降低了其最大的频率变化量(从0.28 Hz到0.14 Hz)。图9(c)中不同参数下的两条曲线表明，更大的转动惯量引发了更大的直流母线电压变化量(从35 V到50 V)，因此在获得较低的电网RoCoF与较低的直流母线电压变化量之间需要折中。图9(d)中不同参数下的两条曲线表明，采用大惯量时充电电流变化更平缓。

电网有功功率指令相应变化后，如图9(a)所示，电网频率均在1 s内就恢复到50 Hz，引入Ibat-ωl控制后，表现出轻微的振荡。由图9(b)可知，1 s后LVSM的频率也稳定在50 Hz，但更大的转动惯量使调节过程中的超调更大。由图9(c)可知，电网频率恢复过程中直流母线电压存在暂升或暂降现象，但波动在可接受的范围内，且在1s后恢复至额定值。图9(d)表明，充电电流随着电网频率的恢复而恢复到额定值。

本地负载功率和电网有功功率指令变化后，CC放电模式的电网频率、LVSM频率、LVSM直流母线电压波形与CC充电模式类似，仅充电电流波形沿纵轴平移至小于0处，能量由EV向电网流动，实现了V2G功能。

4.2 CV充电模式

当SOC在CC模式下充电至80%时，切换为CV充电。在CC充电模式下，电池主要工作在如图6所示的额定区域，电池电压基本保持不变，充电装置可近似看作恒功率负载；而在CV充电模式下，充电电流不断降低，充电装置吸收的功率不断减小。由于CV充电模式下充电功率不断降低，需要不断调整电网的有功功率给定才能维持电网频率的稳定，为了体现所提控制策略稳定电网频率的效果，将电网的初始有功功率给定设为与引入Vbat-ωl控制前一致。为了使所提控制策略对电网频率影响的效果更明显，将表2中与电池容量有关的参数(Qfull、Qexp和Qnom)成比例地减小，使CV充电在5 min内完成。本地负载在t=0 s增加24%，电网有功功率指令在t=2 s相应地增加，本地负载在t=4 s减少24%，电网有功功率指令在t=6 s相应地减少。电网频率、LVSM频率、LVSM直流母线电压、充电电流和电池电压的响应过程分别如图10(a)～图10(e)所示。

由图10(a)～图10(c)可知，CV充电与CC充电模式下电网频率、LVSM频率和LVSM直流母线电压响应波形类似。由图10(d)和图10(e)可知，电池电压升高或降低后，充电电流也相应地增加或减小，电池整体的充电功率也随之增加或减小。

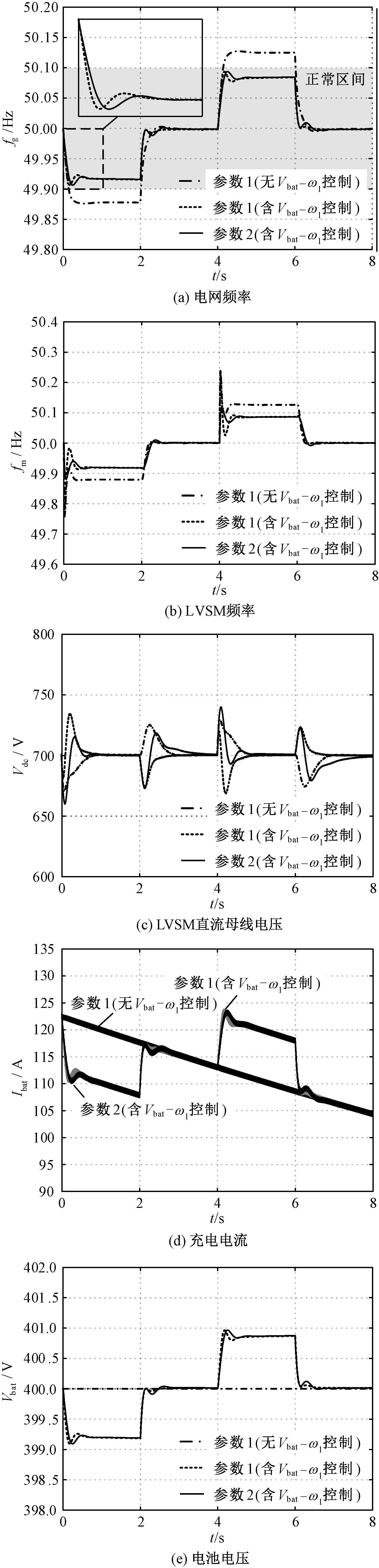
图10 CV充电模式下系统各变量的响应过程

4.3 关键参数灵敏度分析

两级式EV充电桩的关键参数主要有前级LVSM的转动惯量J和阻尼系数D，以及后级DC-DC变流器的网荷互动系数Kibat和Kvbat，主要关注的输出变量为电网频率fg和直流母线电压Vdc。考虑到CC充电和CV充电模式下变功率对fg和Vdc影响的相似性，以CC模式为例，分析本地负载突增时，fg和Vdc对J、D和Kibat变化的敏感度。

保持其他参数不变，选取不同的Kibat、fg和Vdc在本地负载突增24%后变化的情况分别如图11(a)和图11(b)所示。由图11(a)可知，随着Kibat的增加，fg变化EV充电功率的影响增加，稳态时电网频率与额定值的偏差减小；同时，由于动态减载程度的加剧，从图11(b)中可以观察到直流母线电压的跌落量减小，甚至出现了短暂的反向上升。

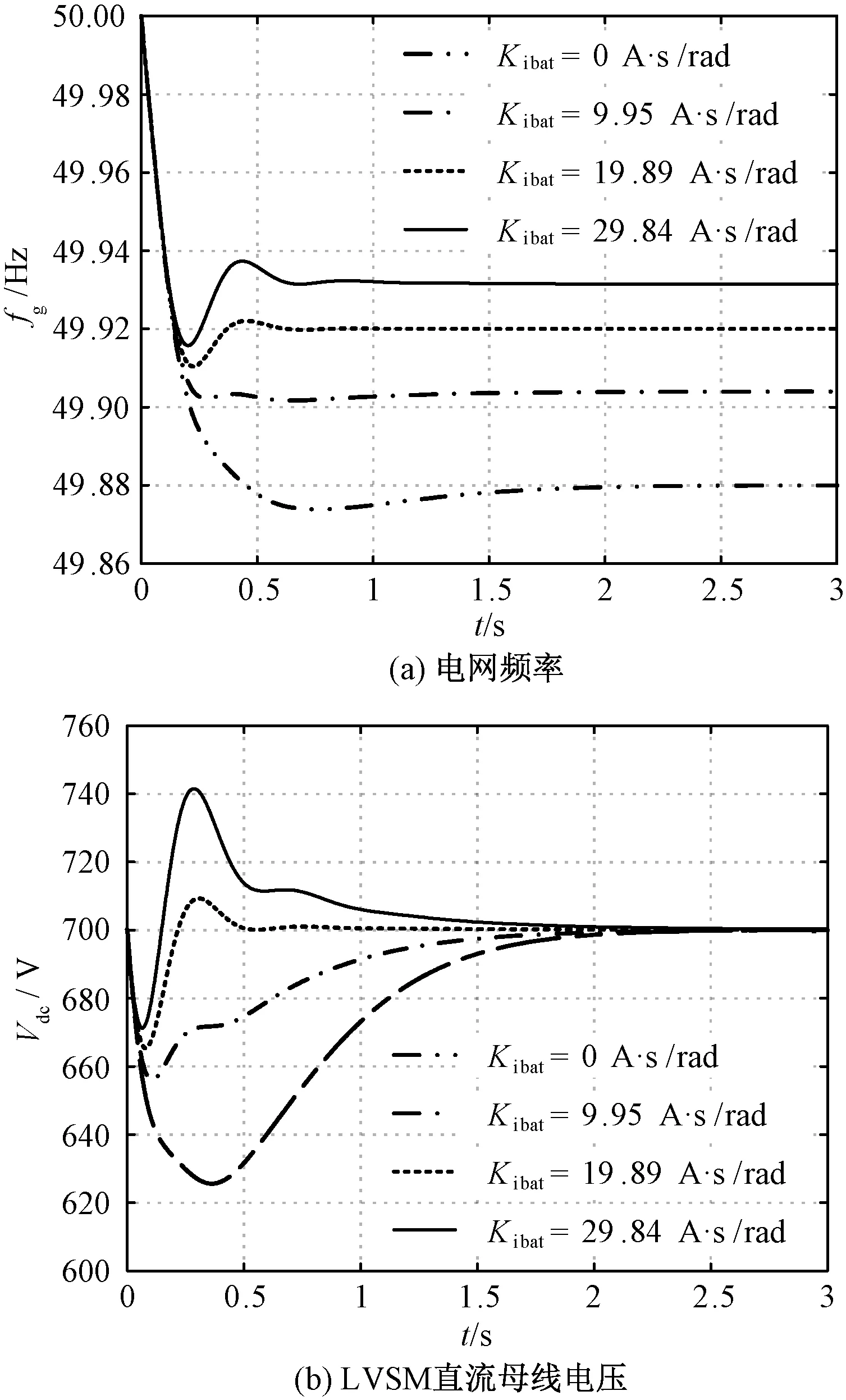
图11 系统变量对Kibat变化的敏感度

保持其他参数不变，选取不同的J、fg和Vdc在本地负载突增24%后变化的情况分别如图12(a)和图12(b)所示。由图12(a)和图12(b)可知，随着J的增加，fg和Vdc的振荡现象均更加明显；由图12(a)可知，由于缺少直流母线电压PI调节器参数的匹配，更大的J并没有显著降低fg的RoCoF。

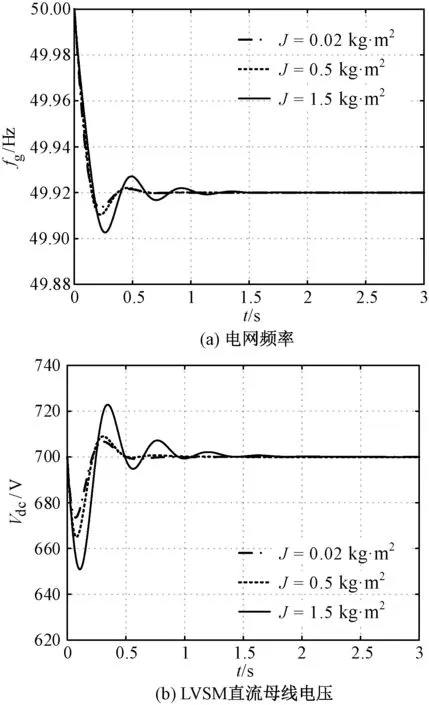
图12 系统变量对J变化的敏感度

保持其他参数不变，选取不同的D、fg和Vdc在本地负载突增24%后变化的情况分别如图13(a)和图13(b)所示。由图13(a)和图13(b)可知，随着D的增加，fg和Vdc的振荡程度逐渐减弱；图13(a)表明由于直流母线电压控制回路的存在，D不会影响fg的稳态值，这是LVSM控制与VSG控制的不同点之一。

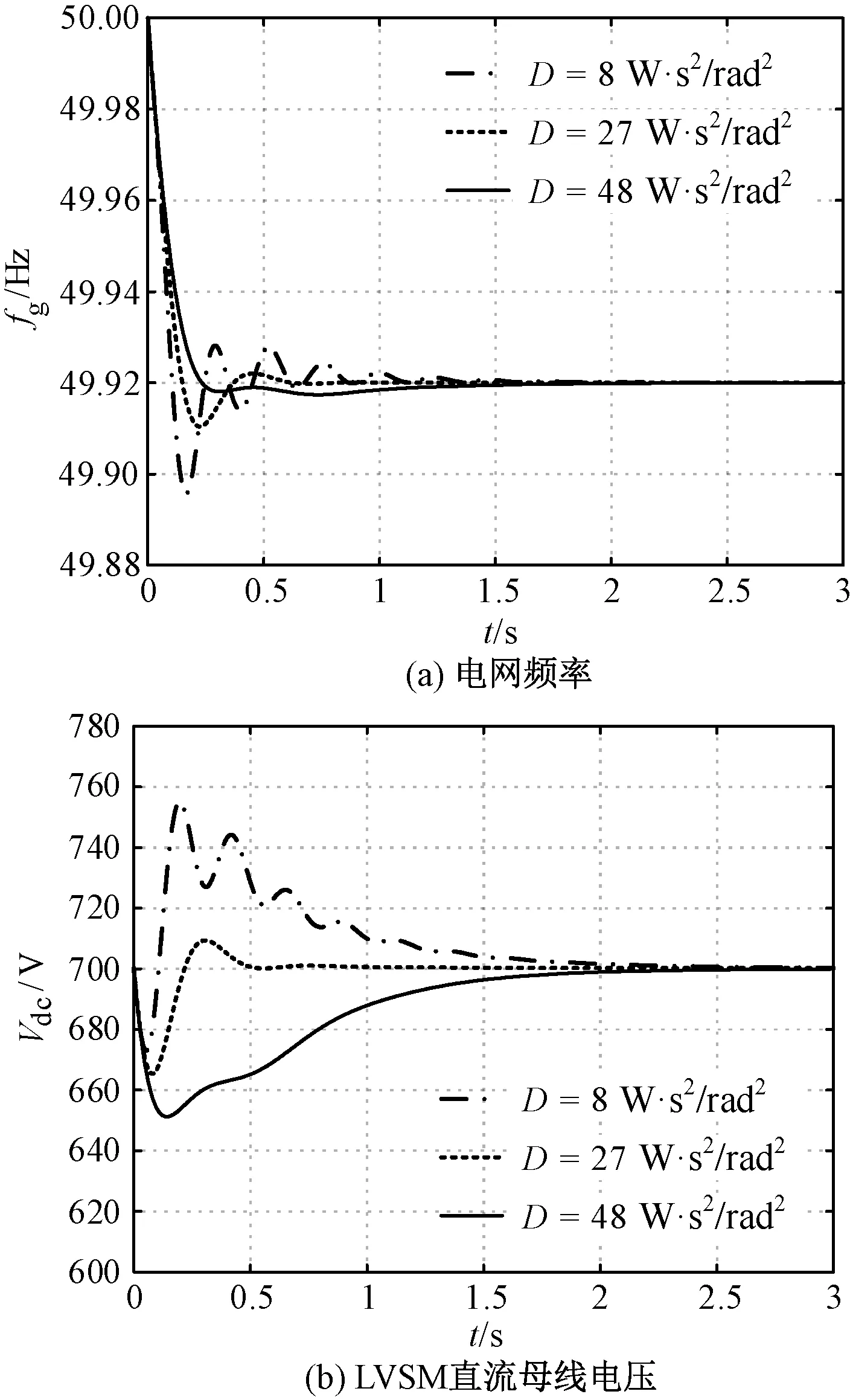
图13 系统变量对D变化的敏感度

5 结论

基于负荷虚拟同步机(LVSM)控制技术，本文提出了一种适应电网频率变化的电动汽车充放电控制策略，通过网-荷互动提高了电网频率的稳定性。仿真结果表明，引入本文所提的控制策略后，在电动汽车CC充-放电和CV充电的情况下，通过适当调整充/放电的电流或电压值均能降低本地负载突变引起的电网频率变化量，使电网频率保持在正常工作区域内。此外，LVSM转动惯量更大时，电网频率的变化率更低，但由于大转动惯量更易诱发振荡特性，需要其他控制参数的匹配。分析直流母线电压波形可知，在获得较低的电网频率变化率与较低的直流母线电压变化量之间存在折中，需要进一步优化。本文的研究对提高电网对大规模电动汽车接入的适应性，使电动汽车负荷具有一定的需求侧响应调节能力，减轻大功率电动汽车负荷对电网的影响具有重要意义。