可用于短舱结构的机织复合材料几何参数对力学性能的影响分析

李京菁

(上海飞机设计研究院，上海 201210)

0 引言

机织复合材料具有较高的比刚度、比强度、较好的面内力学特性、抗腐蚀及抗疲劳特性，被广泛应用于航空航天领域，尤其是民用航空领域。随着我国自主研制的民用客机C919、CR929及民用航空发动机的研发[1-2]，先进复合材料因其重量轻、油耗低、污染低以及成本低等方面的优势为民用飞机的进一步发展提供了有利的保证。而短舱结构包含大量非主承力的功能性结构，故基于机织复合材料的这些优点可被大量用于飞机发动机短舱结构上。

由于机织复合材料自身的结构特点，相较于铺层复合材料，机织复合材料引入了更多的几何参量。而在实际应用过程中，机织复合材料会遭遇更多问题，如成型过程中机织复合材料由于受到模具挤压而造成局部区域变形过大而造成力学性能的变化。故本文通过讨论机织复合材料的几何参量对其力学性能的影响深入了解机织复合材料的力学特性。

目前，对机织复合材料的仿真分析可以分为细观、宏细观和宏观三种尺度下的仿真分析。细观的优势是可以完全模拟机织结构的几何形态、纤维束形态，计算结构准确但计算量巨大，且不方便修改结构参数；宏细观尺度下的仿真分析同样可以反应结构的几何形态，计算精确但计算量也较高且参数修改不方便，不利于几何形态对力学性能的研究；宏观尺度下的仿真分析需要精细的算法将各个参数添加到仿真模型中，参数修改反应迅速但会牺牲精确性[3-9]。本文基于宏观尺度，对PD模型[10]进行修正，校核了修正后的PD模型的可靠性，同时系统地分析了纤维束宽度、纤维束厚度、纤维束间间距、波动角、编织角、纤维体积比等几何参数对力学性能的影响，克服了三维细观有限元模型几何参数的改变所带来的重新建模的巨大工作量。同时，由于平纹机织复合材料中某些参数之间的耦合作用，因此对所要讨论的几何参数做了优化，并利用机织复合材料的厚宽比、间隙比分别讨论了波动角对机织复合材料力学性能的影响，大大降低了因几何参数之间的耦合关系而造成的几何参数对机织复合材料力学性能影响的复杂程度。

1 材料性能数据及几何参数

本文以E-Glass/Epoxy以及Graphite/Epoxy平纹机织复合材料讨论几何参数对机织复合材料力学性能的影响，材料参数详见表1。

图1 平纹机织复合材料结构示意图

表1 纤维及基体的基本材料力学性能[12]

表2 平纹机织复合材料的几何参数[12]

2 问题的引入

本文基于PD模型讨论几何参数对机织复合材料性能的影响。在PD模型中，考虑到对于大多数平纹机织复合材料而言其波动角一般为一极小量，且沿纤维束走向的变化不明显[11]。因此为了简化起见，在PD模型里假设波动角满足：

β=tanβ

(1)

且同时选取β的最大值作为PD模型的波动角的输入，即：

(2)

表3为基于PD模型计算获得的E-Glass/Epoxy平纹机织复合材料及Graphite/Epoxy平纹机织复合材料的计算结果对比情况。由表3可以看出，对于E-Glass/Epoxy机织复合材料而言，PD模型的预测结果较好，但对Graphite/Epoxy机织复合材料的E1及E2弹性模量的预测结果并不理想，PD模型及MMPM模型所预测的材料弹性性能均远远高于其它几组模型的预测结果。而PD模型与MMPM模型具有一个共同特点：均假设机织复合材料的波动角为一极小值，这为PD模型的修正提供了思路。

表3 几种计算模型预测结果的对比

3 几何参数对力学性能的影响

本文将基于PD模型，并通过对模型的修正，重点讨论几何参数对机织复合材料力学性能的影响。

3.1 波动角β对平纹机织复合材料力学性能的影响

波动角作为一个直接影响机织复合材料力学性能的重要因素并不是独立存在的。波动角的大小会受到材料其它几何输入量如纤维束厚度H、纤维束宽度A及纤维束之间间距G的影响。这三个几何输入量之间的相互作用共同决定着材料波动角β的大小，而这些相互作用具体体现在材料的厚宽比(H/A)和间隙比(G/A)上。

在PD模型中引入波动角[13-19]，根据纤维束波动形态的正弦曲线假设对PD模型进行修正。其中，波动角β可以表示为：

(3)

其中，波动角的最大值为：

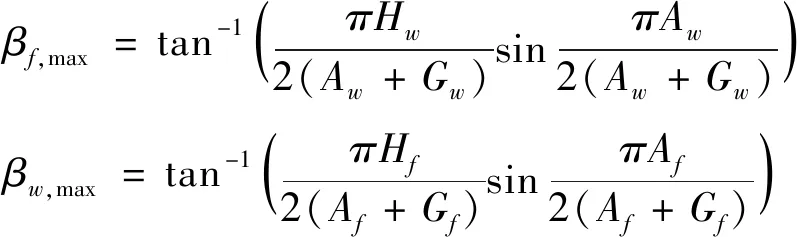
(4)

或

(5)

其中，波动角的最大值为：

(6)

波动角推导公式：公式(3)及公式(4)分别来自于Naik和Ganesh的SAM模型以及MKM模型。利用这两组公式对逐步失效模型中关于波动角的计算过程进行修正，同时分别建立PWC_HEM-SAM模型和PWC_HEM-MKM模型。根据各个模型预测结果的对比情况说明波动角对机织复合材料的力学性能所产生的影响。

3.1.1 厚宽比(H/A)

图2为平纹机织复合材料的厚宽比对材料弹性模量E1或E2(E1=E2)的影响，以及几种模型不同预测结果的对比情况。图中的三条曲线分别描述了PD模型、PD_SAM模型以及PD_MKM模型所获取的弹性模量E1随厚宽比变化的变化趋势。由图2可以看出当厚宽比小于0.07时三类模型的预测结果差异不大；当厚宽比大于0.1时开始出现明显差异，材料的弹性模量E1均随着厚宽比的增大而降低；当厚宽比取0.25时即为Graphite/Epoxy平纹机织材料的取值，可以看出：PD模型所预测的结果远远大于除MMPM模型以外其它模型的预测值。而修正后的PD_SAM模型与PD_MKM模型的预测结果处于几种预测结果的集中区域。由此可以得到如下结论：对于Graphite/Epoxy机织复合材料而言波动角的影响不可忽略。

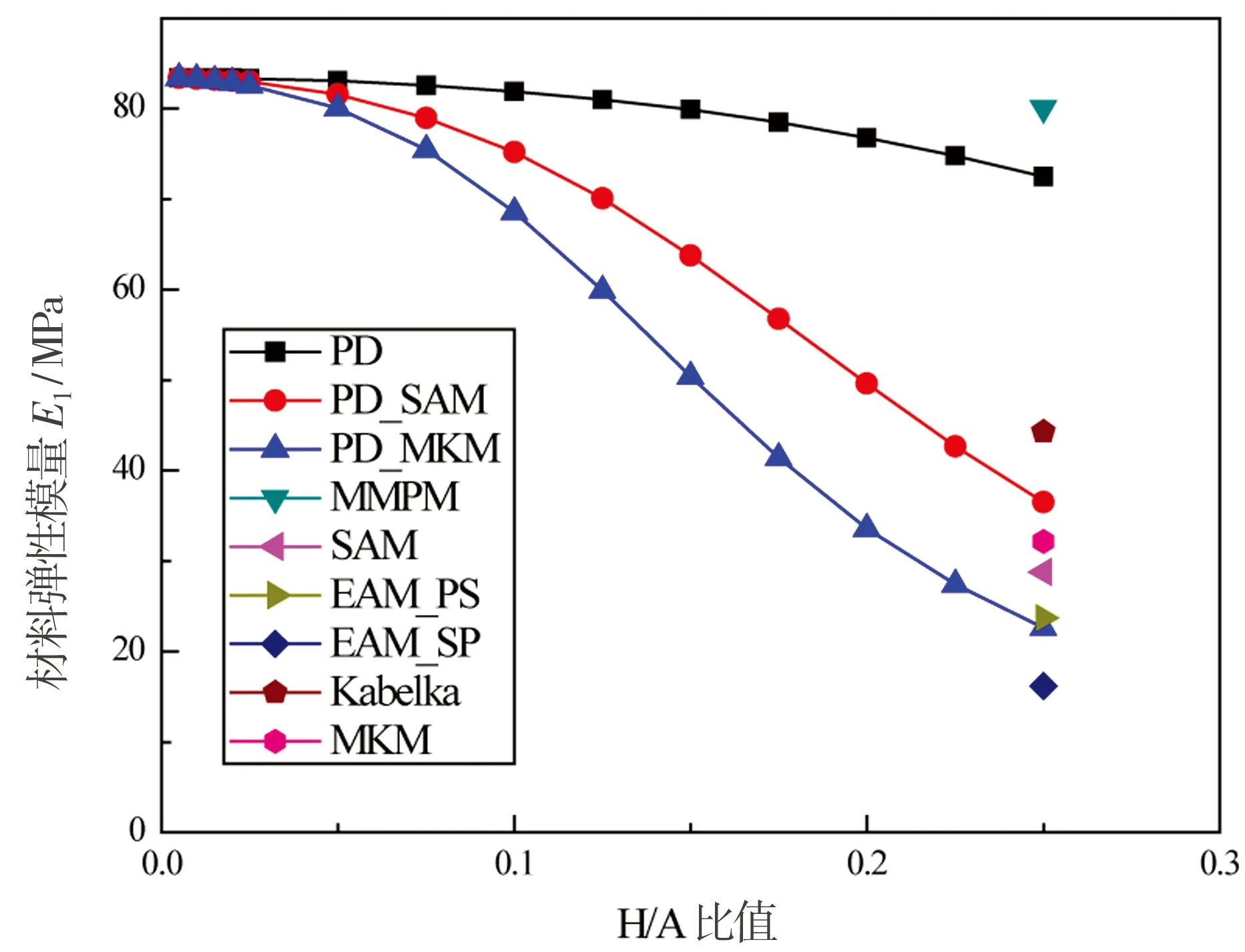
图2 Graphite/Epoxy平纹机织复合材料的厚宽比(H/A)对弹性模量E1的影响

图3为材料弹性模量E3受厚宽比的影响曲线。同E1和E2的预测结果相比，弹性模量E3受厚宽比的影响较小，即材料的波动角对弹性模量E3的影响较小，且基于波动角求解方式不同的三类预测模型所预测的结果所存在的差异也较小。

图4和图5分别描述的是材料的厚宽比对剪切模量G12和G23的影响。由图可以看出，宽厚比对材料面内剪切模量影响较小，且与其它模型的预测结果一致，但对于面外剪切模量而言，波动角的影响相对于面内剪切模量的影响较大，这是由于波动角导致的面外方向上纤维含量的增大。

图3 Graphite/Epoxy平纹机织复合材料的厚宽比(H/A)对弹性模量E3的影响

图4 Graphite/Epoxy平纹机织复合材料的厚宽比(H/A)对弹性模量G12的影响

图5 Graphite/Epoxy平纹机织复合材料的厚宽比(H/A)对弹性模量G23的影响

图6为E-Glass/Epoxy平纹机织复合材料的厚宽比对材料弹性模量E1或E2(E1=E2)的影响。通过与图2的对比情况可以看出厚宽比对E-Glass/Epoxy机织复合材料弹性模量的影响相对较小，尤其是对弹性模量E1的影响。当厚宽比取0.25时，PD模型对Graphite/Epoxy机织复合材料弹性模量预测结果几乎是修正后的PD_SAM及PD_MKM模型预测结果的两倍，而对于E-Glass/Epoxy机织复合材料而言三类模型的预测结果的差值仅为20%。由此可见，不同材料对厚宽比的敏感性不同。对于Graphite/Epoxy材料而言，纤维和基体的力学性能存在着较大的差异，其中Graphite的弹性模量E1为388 GPa，而Epoxy的弹性模量E1仅为3.5 GPa，几乎仅占纤维弹性模量的0.9%。而E-Glass/Epoxy中纤维的弹性模量E1为72 GPa，基体模量则占纤维模量的4.9%。由此可以得出如下结论：当纤维与基体的力学性能存在较大差异时，材料的厚宽比所造成的影响也就较大。由此可以看出材料类型和厚宽比在一定程度上共同决定着材料的力学性能。

图6 E-glass/Epoxy平纹机织复合材料的厚宽比(H/A)对弹性模量E1的影响

3.1.2 间隙比(G/A)

作为另外一种协同作用，间隙比用来同时说明材料的波动角对平纹机织复合材料力学性能的影响。通过讨论间隙比对均衡型E-Glass/Epoxy平纹机织复合材料力学性能的影响，同时对比厚宽比对E-Glass/Epoxy平纹机织复合材料力学性能的影响说明两种形式的协同作用对波动角的影响及趋势。

图7为间隙比对E-Glass/Epoxy平纹机织复合材料弹性模量E的影响，弹性模量E1或E2(E1=E2)随间隙比的增大略有增大，而弹性模量E3的变化不明显。图8为间隙比对材料剪切模量的影响，剪切模量G12随间隙比的增加而增加，而剪切模量G13则随间隙比的增加略有降低。

图7 E-Glass/Epoxy平纹机织复合材料的间隙比(G/A)对弹性模量E的影响

图8 E-Glass/Epoxy平纹机织复合材料的间隙比(G/A)对弹性模量G的影响

图9为E-Glass/Epoxy平纹机织复合材料的间隙比及宽厚比与波动角之间的关系，由图可以看出，间隙比与厚宽比对材料力学性能的影响是相反的。这是由于间隙比造成材料波动角的减小而导致面内纤维向材料力学性能的增强；而厚宽比则相反，厚宽比的增加会导致材料波动角的增大，从而导致面内纤维向材料力学性能的损失。

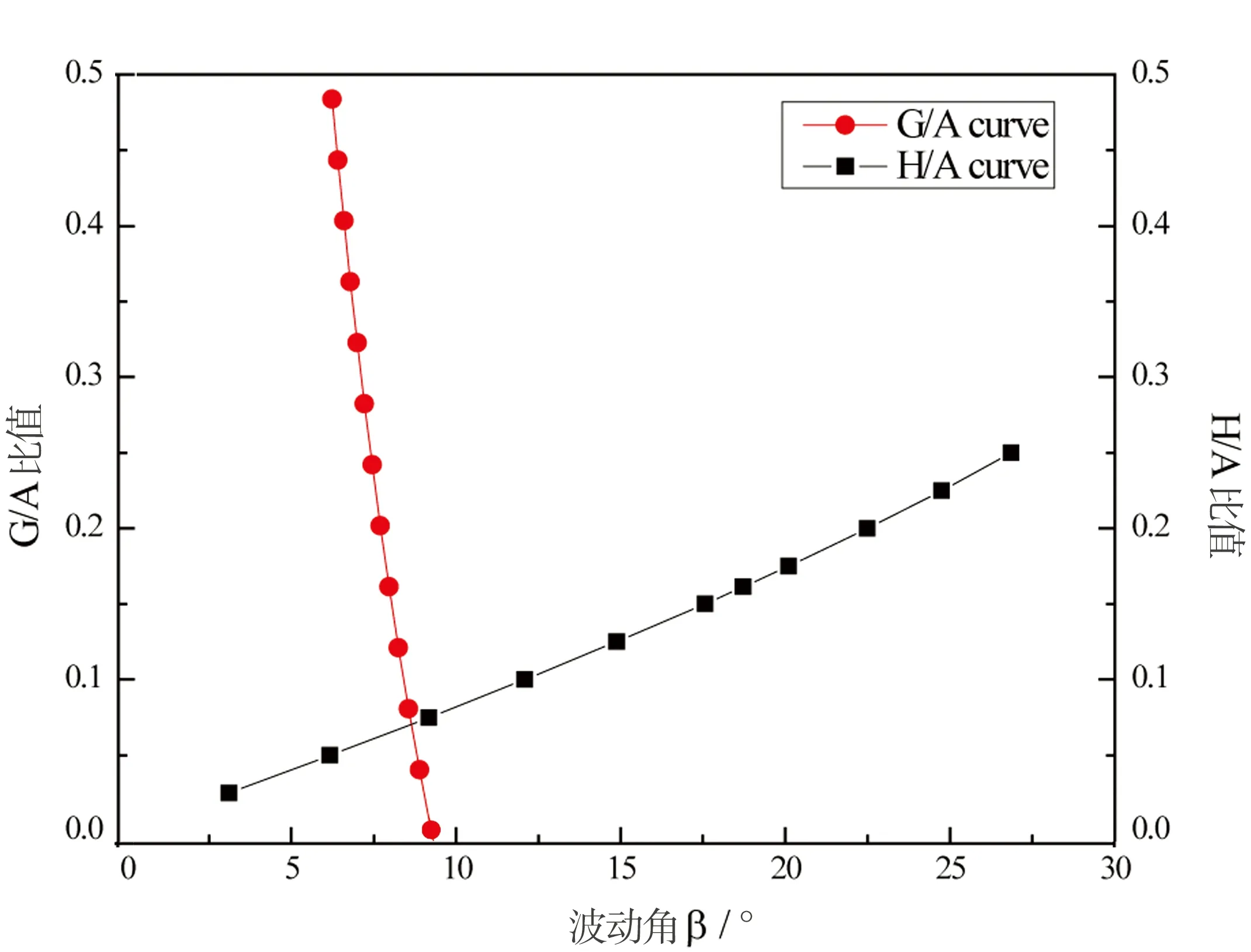
图9 E-Glass/Epoxy平纹机织复合材料的间隙比(G/A)及宽厚比(H/A)与波动角β之间的关系

3.2 编织角θ对机织复合材料力学性能的影响

对于机织复合材料而言波动角β及编织角θ作为两个重要几何参数直接决定着机织复合材料的力学性能。波动角对于大多数机织复合材料而言均处于一个极小量，且影响较小，仅有个别材料会对相对较大的波动角出现较高的灵敏度，如Graphite/Epoxy机织复合材料。而编织角与波动角不同，它直接改变了材料类型及其力学性能。

图10及图11分别描述的是编织角由-90°到90°变化的过程中二维双向机织复合材料E-Glass/Epoxy材料的弹性模量、剪切模量及泊松比的变化过程。由图10可以看出，当编织角的值取近似0°时，二维双向机织复合材料将转化为单向复合材料，且其弹性模量E1取最大值；当编织角取±90°时，材料的弹性模量E1的取值最小。而弹性模量E2的变化趋势与E1相反，弹性模量E2随着编织角度的增大而增大，当编织角取±90°时弹性模量E2取最大值，且此时E2与E1的取值相等，也即此时材料的类型为平纹机织复合材料。而弹性模量E3几乎不受编织角度的影响，且保持一个定值。

图10 E-Glass/Epoxy平纹机织复合材料的编织角θ的变化对弹性模量E的影响

图11 E-Glass/Epoxy平纹机织复合材料的编织角θ的变化对剪切模量G的影响

图11所描述的是E-Glass/Epoxy平纹机织复合材料剪切模量与编织角之间的变化关系。由图可以看出剪切模量G12在编织角取±45°时值最大；而剪切模量G13与G23和G12相比受编织角的影响较小，且当编织角取±90°时G13与G23相等，这一特性满足复合平纹机织复合材料的力学特征。

3.3 编织总体纤维体积分数对机织复合材料力学性能的影响

当机织复合材料的几何形态保持不变的情况下，即材料的厚宽比、间隙比以及编织角均取定值时，总体纤维体积比将作为决定机织复合材料力学性能的唯一重要参数。它决定着机织复合材料中纤维的含量，而总体纤维比与纤维束纤维体积比之间存在一定的比例关系，见公式(7)。

(7)

图12 总体纤维体积分数对弹性模量E的影响

图13 总体纤维体积分数对剪切模量G的影响

图12为总体纤维体积比对弹性模量E的影响，由图可以看出弹性模量E1或E2(E1=E2)受总体纤维体积比的影响较大，它们随着总体纤维体积比的增加而增大，且随着总体纤维体积比的增加其增大的趋势也越来越快，呈现一种指数关系的形式。而总体纤维体积比对E3的影响不明显。图13显示的是总体纤维体积比对材料剪切模量G的影响，由图可以看出剪切模量随总体纤维体积比变化的趋势与弹性模量类似，剪切模量G12与总体纤维体积比存在明显的指数关系，随着总体纤维体积比的增加G12的大小则急速增长，且总体纤维体积比越大效果越明显。而剪切模量G13及G23的变化则随总体纤维体积比的变化不明显。

4 结论

本文分别通过机织复合材料的波动角θ、编织角β以及总体纤维体积比分析了机织复合材料的几何参数对其力学性能的影响。同时，根据机织复合材料的几何形态对波动角进一步划分，分别讨论了厚宽比H/A以及间隙比G/A与波动角之间的关系，讨论了它们对材料力学性能的影响，最终明确了各个参数对材料性能的影响。

几何参数对材料力学性能的影响可以总结如下：

(1)对于大多数材料的平纹机织复合材料而言，其波动角一般处于一个极小值，且波动角的影响可以忽略不计，但对于部分材料其波动角的影响比较明显。例如Graphite/Epoxy平纹机织复合材料，当机织复合材料中纤维与基体的材料属性的差距较大时，波动角对该机织复合材料力学性能的影响就不可忽略，随着波动角的增大材料的力学性能有明显的弱化，如果忽略波动角的影响会造成预测结果的巨大差异。而对于E-Glass/Epoxy平纹机织复合材料而言，虽然材料的力学性能在较大波动角的影响下有所变化，但其影响并不明显。

(2)厚宽比与间隙比对波动角的影响相反，厚宽比增大则波动角增大，而间隙比增大波动角则减小。且随着波动角的增大，平纹机织复合材料的弹性模量E1及E2的大小有所减小，而对弹性模量E3及剪切模量大小的影响并不明显。

(3)编织角对机织复合材料力学性能的影响比波动角显著，它能够直接决定材料的类型及其力学性能。当偏轴向纤维束绕着主轴向纤维束转动的过程中，材料的力学性能会按照一定形式波动，使材料的力学形态在单向复合材料与平纹机织复合材料的力学性能中相互转变。

(4)机织复合材料的总体纤维体积比对平纹机织复合材料力学性能的影响也较为明显。在其它几何参数不变的情况下，总体纤维体积比直接决定着纤维束的力学性能。总体纤维体积比越大纤维束的力学性能也就越强，机织复合材料的力学性能也就越强，且这一增长趋势接近于指数增长，即当总体纤维体积比越大时，材料力学性能的增长就越快。