基于K均值聚类与小波变换的噪声图像分割研究

谢玮昌 李宪华 凤志雄 来淼

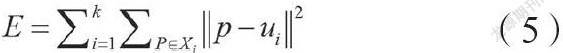
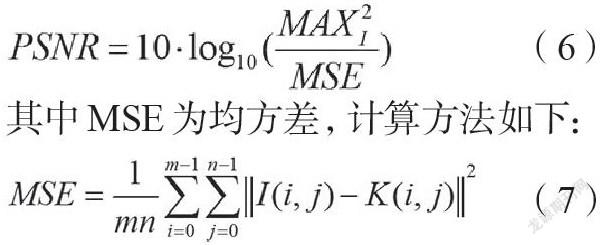
编者按：这篇文章针对传统模糊C均值的分割方法容易受到噪声影响的问题，设计了一种基于小波变换和K-means聚类的噪声图像分割方法。首先，对噪声图像进行二维小波分解，然后对分解后的噪声系数进行阈值处理，抑制噪声影响，将阈值处理后的系数进行小波逆变换重构输出图像，最后，对小波变换后的图像进行K-means聚类分割。实验结果表明，将原始噪声图像和降噪后图像进行图像分割对比，发现降噪后分割效果更好，所用时间更短。

引言

图像分割是一种重要的图像分析技术，是图像分析的第一步。它是指将图像中具有特殊意义的不同区域划分开来，这些区域是互不相交的，每个区域满足灰度、纹理、彩色等特征的相似性准则。图像分割是图像分析过程中最重要的步骤之一，分割出的区域可以作为后续特征提取的目标对象[1]。

在获取、传输或变换图像过程中受到外界影响会产生噪声，使图像对比度下降或者模糊。图像降噪是指减少数字图像中噪声的过程，被广泛应用于图像的预处理。模糊C均值（FCM）是常用的图像分割技术，该方法是由Dunn提出，经过Bezdek的推广后，获得了较广泛的应用[2]。然而这一算法也存在着一些缺点，初始化选取不合适会影响分割效果，数据样本较大时聚类时间较长，且容易受到噪声的影响[3]。而在给定聚类中心数目后，K均值聚类方法的运算时间会大大小于模糊C均值。

对此本文提取基于小波变换与K-means均值聚类的噪声图像分割方法。首先对噪声图像进行小波变换重构，去除随机噪声，然后对重构后的图像使用K-means算法进行图像分割。實验结果表明所提方法可以有效去除噪声的影响，且分割时间较短。

阈值降噪模型

小波变换

当需要精确的低频信息时，采用长的时间窗;当需要精确的高频信息时，采用短的时间窗。小波变换用的不是时间-频率域，而是时间-尺度域。尺度越大，采用的时间窗越大，尺度越小，采用的时间窗越短，即尺度与频率成反比[4]。

对于任意的函数f（t）∈L2（R），其连续的小波变换为：

为了使信号重构的实现在数值上是稳定的，除了完全重构条件外，还要求小波ψ（t）的傅里叶变换要满足稳定性条件。图像经小波分解后会获得低频分量L和高频分量H，对变换所得数据的每一列进行分解，获得原始图像在水平和垂直方向上的低频分量LL、水平方向上的低频和垂直方向上的高频LH、水平方向上的高频和垂直方向上的低频HL以及水平和垂直方向上的高频分量HH。对分解后的分量进行处理输出后，可以获得降噪图像。

小波阈值处理

原始图像在添加噪声后，进行小波分解，所得到图像的小波系数幅值要比噪声的系数幅值大。将噪声图像经过小波分解后，保留低频信号分解值，对于高频信号，可以设定一个阈值，对于高于这个阈值的系数予以清零，低于这个阈值的系数则保留，最后将处理后的小波系数进行小波逆变换重构，获得输出图像。

基于K-means算法的图像分割

K-means之图像分割

K-means聚类算法简捷，搜索能力强，广泛应用在大量数据处理方面，其中包括数据挖掘和图像处理。采用K-means进行图像分割，将图像的灰度作为样本，构建整个样本空间，从而把图像分割任务转换为对数据集合的聚类任务。然后进行图像区域分割，最后抽取图像区域的特征。

K-means算法首先从数据样本中选取K个点作为初始聚类中心;其次计算各个样本到聚类的距离，把样本归到离它最近的那个聚类中心所在的类;然后计算新形成的每个聚类的数据对象的平均值来得到新的聚类中心;最后重复以上步骤，直到相邻两次的聚类中心没有任何变化，说明样本调整结束，聚类准则函数达到最优[6]。

K-means聚类算法原理

（1）选定某种距离作为数据样本间的相似性度量

在计算数据样本之间的距离时，可以根据实际需要选择某种距离（欧氏距离、曼哈顿距离、绝对值距离、切比雪夫距离）作为样本的相似性度量，其中最常用的是欧氏距离。

（2）聚类中心迭代终止判断条件

K-means算法在每次迭代中都要考察每个样本的分类是否正确，若不正确，则需要调整。在全部样本调整完毕后，再修改聚类中心，进入下一次迭代，直到满足某个终止条件。

① 不存在重新分配给不同聚类的对象;

② 聚类中心不再发生变化;

③ 误差平方和准则函数局部最小。

（3）误差平方和准则函数评价聚类性能

假设给定数据集X包含k个聚类子集X1，X2，…，Xn，各个聚类子集中的样本数量分别为n1，n2，…，nk，各个聚类子集的聚类中心分别为μ1，μ2，…μk，则误差平方和准则函数公式为：

算法步骤：

步骤一，选择要聚类的类别数目k，即选择k个中心点。

步骤二，针对样本空间中的点，寻找距离其最近的中心点，与其距离最近的中心点分为一类，这样完成了一次聚类。

步骤三，判断聚类前后的样本点的类别情况是否相同，如果相同，则算法终止，否则进入步骤四。

步骤四，针对每个类别中的样本点，计算这些样本点的中心点，当做该类的新的中心点，继续步骤二。

实验分析

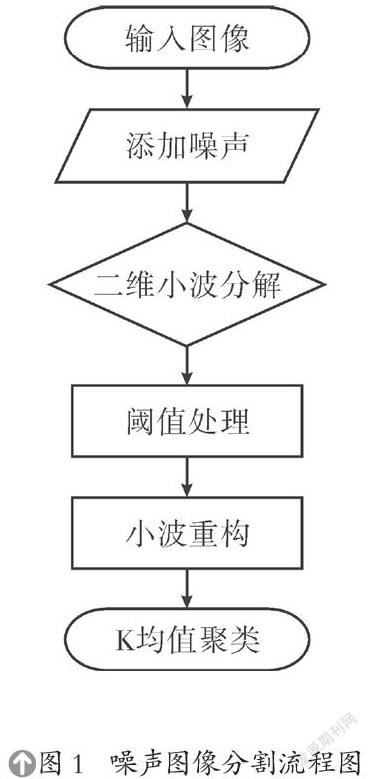
本文的实验流程图如图1所示，首先选取典型的5张灰度图像，然后添加噪声，获得含噪声的灰度图像。对添加噪声后的图像进行二维小波分解，分解后的小波系数进行阈值处理，阈值处理后的小波系数进行小波逆变换重构，输出降噪后图像，对降噪后的图像进行K均值聚类。

本次实验的条件是Windows10系统，CPU：AMD 3600，软件：MATLAB 2020b。为了验证所提出的方法的降噪和分割能力，如图2所示选取五张典型的灰度图像，分别命名为img1，img2…img5。

对原图添加随机噪声，如图3所示。

将添加了高斯噪声的图3通过小波变换重构进行降噪，如图4所示。

对进行小波降噪重构后的图4进行K均值聚类分割，其分割效果如图5所示。

為了验证本文方法的抗噪能力，引入峰值信噪比（PSNR）来进行评价。PSNR[7]值越大则表明抗噪性能越好。

其定义为：

其中MSE为均方差，计算方法如下：

MAX表示图像中像素最大值，I，K表示降噪前后的图像，如表1所示，在进行小波降噪后，K均值聚类的PSNR值可以获得较大提升，说明所提方法降噪效果较好。

同时将本文图像分割算法运算时间与FCM分割算法运算时间相比，在MATLAB程序中添加tic，toc计时函数计算算法完整运行一次所需时间。如表2所示，本文算法运算时间相比于FCM大大减少。

结论

首先将灰度图像添加随机噪声，然后对噪声图像进行小波分解重构，对噪声系数进行阈值处理剔除噪声系数，最后用K均值聚类对降噪后的图像进行分割，并引入峰值信噪比评价本文的降噪能力。实验结果表明本文所提方法具有很好的降噪能力且图像分割时间短。

参考文献：

[1]张铮，徐超，任淑霞，等.数字图像处理与机器视觉[M].北京：人民邮电出版社，2014.

[2]丁震，胡钟山，杨静宇，等.FCM算法用于灰度图象分割的研究[J].电子学报，1997（05）：39-43.

[3]李旭超，刘海宽，王飞，等.图像分割中的模糊聚类方法[J].中国图象图形学报，2012，17（04）：447-458.

[4]张岩.MATLAB图像处理超级学习手册[M].北京：人民邮电出版社，2014.

[5]石雪松，李宪华，孙青，等.基于人工蜂群与模糊C均值的自适应小波变换的噪声图像分割[J].计算机应用，2021，41（08）：2312-2317.

[6]刘衍琦，詹福宇.MATLAB图像与视频处理实用案例详解[M].北京：电子工业出版社，2015.

[7]王敏，周磊，周树道，等.基于峰值信噪比和小波方向特性的图像奇异值去噪技术[J].应用光学，2013，34（01）：85-89.