两种隧道场景下车对车无线信道衰落特性的测量与分析

张旭 姜苏英 杨汨 王威 何睿斯 侯俊 刘鑫一

（1.长安大学，西安 710064；2.北京交通大学，北京 100044）

引 言

物联网(internet of things, IOT)是一个由互联网通过信息传感设备实现现实世界人、机、物等各类要素在任何时间、任何地点互联的巨大网络[1]，其在城市智能交通系统中的车联网(internet of vehicle,IOV)技术就是5G的一个具体应用. 随着移动无线通信技术在交通领域里被广泛使用，智能交通得到了蓬勃发展. IOV技术将无线通信和传感检测技术相结合，收集和交互车辆、道路、环境信息，通过车到一切(vehicle to everything, V2X)的链路，实现交通管理控制、车辆控制和动态信息服务的智能综合网络[2-3]，从而使交通系统的安全性、便捷性和可靠性都得到很大的提升，并为未来无人驾驶系统提供了广阔的发展空间和技术支持. 因此，无线通信技术是支撑智能交通系统发展的一个关键技术.

V2X主要分为三类：车-车(vehicle to vehicle,V2V)、车-基 础 设 施(vehicle to infrastructure, V2I)、车-行人(vehicle to pedestrian, V2P)，通过相互通信构成车载自组网络(vehicle ad hoc networks, VANETs).V2V通信不需要固定基站，而是两个移动车辆从一端到另一端的直接无线通信. 在智能交通系统中，V2V通信起着重要的作用，是无人驾驶、自主预测汽车防撞等应用的关键技术支撑.

为了更好地发展V2V通信系统，对于V2V无线传播信道的准确描述和建模是尤为重要的[4-5]. 它是推动通信标准的建立、促进相关设备的制造以及测试无线通信算法的重要一环，这些都需要通过实际的V2V信道测量活动来对其无线信道进行分析和建模.

近年来，针对典型环境(如农村、郊区、城市和公路)进行了许多V2V无线信道的测量活动和信道建模研究工作[6-8]. 其他特殊环境如地下停车场和隧道等也略有研究，但是针对隧道内和隧道连接处的小尺度衰落研究还不够深入. 文献[9]针对隧道内5.9 GHz V2V传播信道小尺度衰落进行了统计分析，结果表明，测量数据的统计特征符合莱斯分布，隧道外莱斯K因子的平均值高于隧道内的值. 此外，对隧道内尤其是隧道连接处的其他衰落特性如瑞利分布、威布尔分布的研究是有必要的.

本文针对隧道环境下5.9 GHz和5.2 GHz频段的信道进行了测量，并以测量数据为基础，对隧道内外及其连接部分的接收功率和小尺度衰落特性进行了分析. 我们将接收信号幅度的统计特性与五种典型的理论衰落分布进行了比较，发现接收信号的小尺度衰落特性符合具有最小拟合优度值的莱斯分布.此外，计算并分析了莱斯K因子，结果显示隧道内K因子与收发距离有相关性.

1 测量系统

1.1 测量设备

为了研究隧道无线电信道特征，分别针对两个不同的隧道环境进行了信道测量.

第一次信道测量活动使用的是北京交通大学(Beijing Jiaotong University, BJTU)信道探测仪，该探测仪依赖基于软件无线电系统的射频收发仪器——PXI模块化平台[10]，包括矢量信号发射模块与接收模块、时钟模块、电源模块、数据存储、发射天线/接收天线等模块. 在发射机一端，机箱NI PXIe-1082和矢量信号发射机NI PXIe-5673用于发射中心频率fc为5.9 GHz的正交频分复用(orthogonal frequencydivision multiplexing, OFDM)信号. 测量中采用单输入单输出(single-input single-output, SISO)模式，通过安装在车辆顶部的单个发射天线发送信号. 接收机由机箱NI PXIe-1082和矢量信号接收机NI PXIe-5663组成. 信道探测仪的软件平台采用基于实验室虚拟仪器工程工作台LabVIEW的编程环境，可以有效地对信道测量仪器的硬件设备进行编程和控制.通过适当的软件参数设置，可以提取接收机采集的数据并进行处理、存储和实时显示. 表1列出了5.9 GHz下信道探测系统的参数设置.

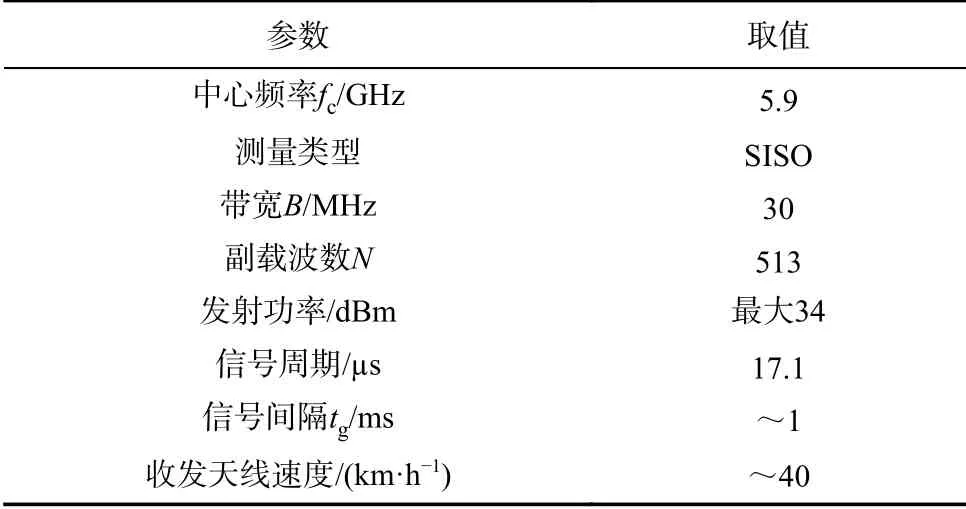
表1 5.9 GHz信道测量系统参数Tab. 1 5.9 GHz measurement parameters

第二次信道测量采用的是MEDAV RUSKDLR宽带信道探测器，发射机发送一个中心频率fc为5.2 GHz的OFDM信号. 信道冲击响应(channel impulse response, CIR)h(tk,τn)每 隔tg时 间 被 测 量 一次，其中：tk=k·tg为 测量时间点，k=1,2,···表示第几次 测 量； τn=n·τΔ,n=0,···,N－1，载 波 数N=1 537；τΔ为时 延 分 辨率. 信 号 带 宽B=120 MHz，对 应 时 域CIR的 τΔ=1/B. 发射信号的周期Tp=12.8 μs决定了最大能够测量出的多径，等效于相对直射路径的绕行最远传播距离为3.84 km. 这一最大距离能够保证在隧道场景下不发生码间干扰，最大传播时延能够被有效地测量. 表2列出了5.2 GHz信道探测参数.

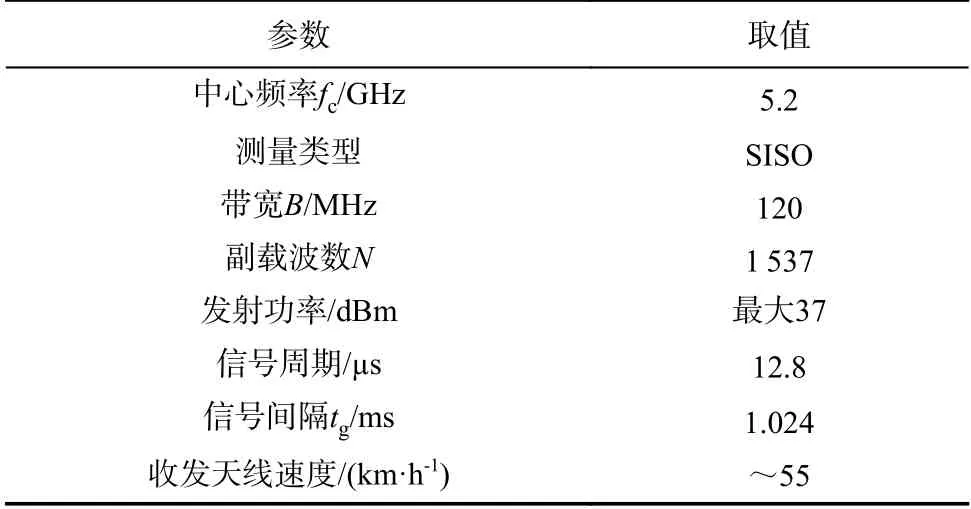
表2 5.2 GHz信道测量系统参数Tab. 2 5.2 GHz measurement parameters

在测量过程中，接收机使用与发射天线相同的天线，收发天线均安装在车辆的车顶，如图1所示.其中左侧的车辆搭载发射机，右侧的车辆搭载接收机.

图1 用于测量的车辆：左侧车辆搭载发射机，右侧车辆搭载接收机Fig. 1 Vehicles used for measurement: the left carries the transmitter and the right carries the receiver

为了保持发射机和接收机的同步，收发两端均采用了铷原子钟来提供稳定的频率标准. 为了控制频率标准随时间发生的偏移，从GPS获得的时间信息被用来驯服铷原子钟. 为了给信道测量仪器提供电源，我们采用大功率逆变器将车载电池的12 V直流电源转换为220 V交流电源. 为了防止电源中断和电流不稳定，逆变器和信道探测仪之间使用了不间断电源.

1.2 测量场景

测量场景一：西安市区南郊的一条双车道矩形隧道(图2(a)). 测量过程中两辆车的行驶速度约为40 km/h，发射车辆在接收车辆的后方同向行驶. 测量从进入隧道前的十字路口开始，在测量过程中，发射机和接收机之间总是存在可视距(line-of-sight，LoS)，所测得的接收功率如图3(a)所示. 从图3(a)可见，接收功率在-55 dBm和-30 dBm之间变化. 在开始的时候，接收到的功率变化不大，是因为这两辆车都在等待交通信号灯从红色变为绿色. 随着发射和接收天线距离的增加，两辆汽车向隧道行驶时，接收功率有了很大的下降. 隧道外接收信号的衰落深度小于隧道内.

图2 两种测量场景Fig. 2 Two measuring scenes

测量场景二：德国慕尼黑郊区Aubing的A96高速公路三车道矩形隧道(图2(b)). 两辆车的行驶速度范围为20～55 km/h，发射车辆在接收车辆的后方同向行驶. 测量从进入隧道前的十字路口开始，在测量活动中，发射机和接收机之间存在LoS和少量的不可视距(non-line-of-sight, NLoS)的情况，所测得的接收功率如图3(b)所示. 从图3(b)可以看出，接收功率在-70 dBm和-50 dBm之间变化. 在开始时接收机已经驶过十字路口向隧道方向行驶，发射机正从十字路口向隧道方向公路拐弯，两车距离逐渐增大，此时有来自前方的大型车辆驶过，两车进入NLoS状态，功率变化剧烈. 在接收机进入隧道后，发射机行驶在进入隧道的公路上，两车处于隧道连接处的状态，在此过程中有大量的汽车位于收发车辆之间，随着发射和接收天线距离的减小，接收功率在经历短暂的骤增骤减后，整体上逐渐增大. 当两辆车都进入隧道后，其衰落深度大于隧道外.

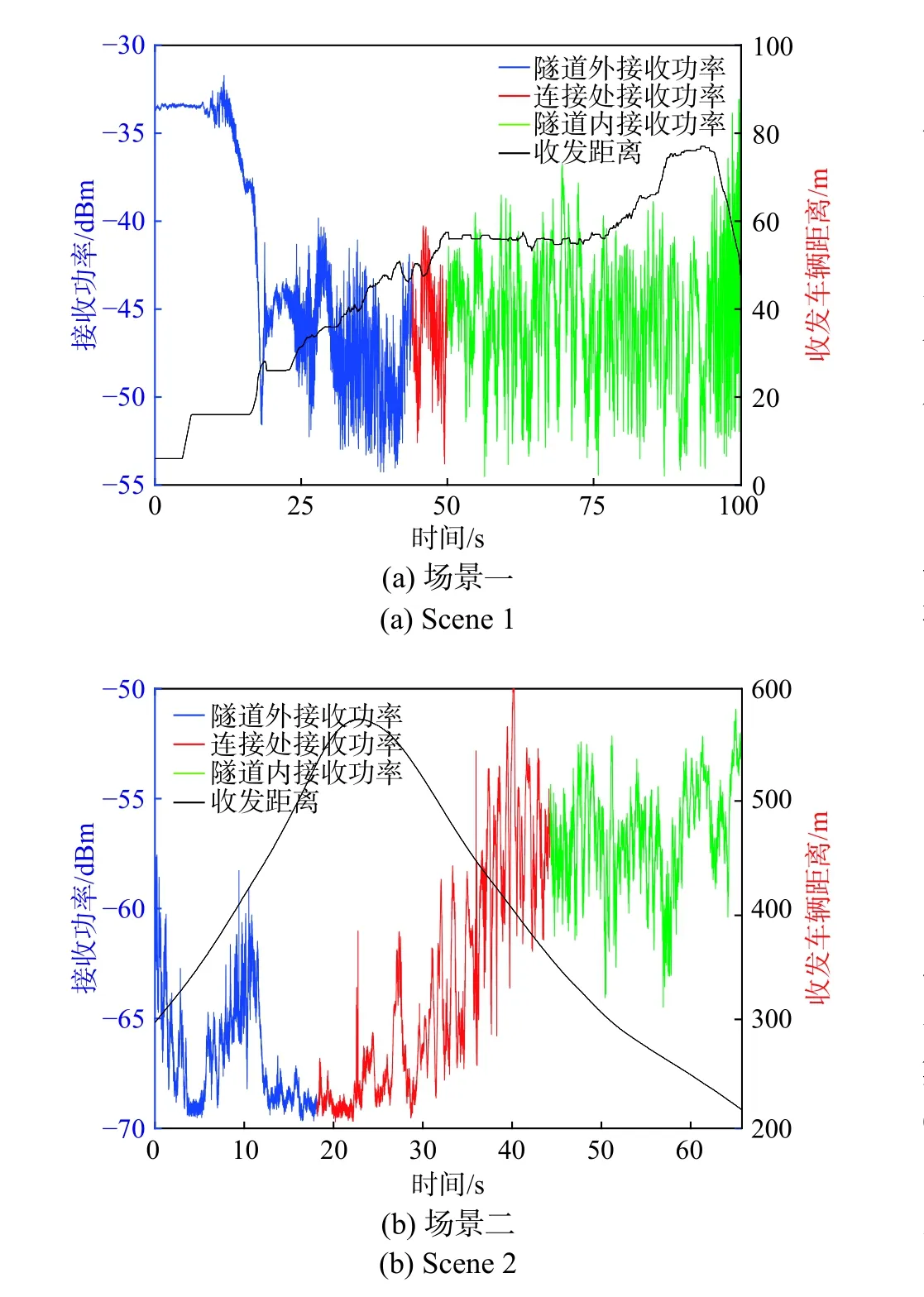
图3 两种场景中的收发车辆距离及功率变化Fig. 3 Distance between two vehicles and received power in two scenes

因此，本文以两段结构相似，但大小有差异的隧道作为研究对象，分析隧道内与隧道连接处的信道传播特性差异.

2 无线信道特性分析

在V2V无线信道的传播环境当中，周围的许多障碍物如车身、墙壁等会形成反射、绕射以及散射等现象，使得电波信号沿多条路径传播后到达接收端. 多径传播信号的幅度、延迟、方向角都可能不相同[11]. 不同的多径分量在接收端叠加起来产生多径效应，导致小尺度衰落. 本节首先基于测量数据对几种路径损耗模型进行验证比较.

2.1 路径损耗模型

路径损耗是一个重要的信道参数，可以用来描述传播信道的大尺度效应[12]. 常见的路径损耗模型包括自由空间传播模型、近距离(close-in, CI)对数传播模型[13-14]和ABG(α-β-γ)路径损耗模型[15]. 在本文中，基于实际测量场景的数据，用发射功率减去一些常见的路径损耗模型得到接收功率模型，用来描述传播信道的大尺度效应.

自由空间损耗模型是无线电波在理想的自由空间中传播，即不存在任何反射、绕射、散射、遮挡等现象的一种理想的传播环境. 在这里被用来作为一个基础的参考模型. 其接收信号强度PR可以表示为

式中：d0为参考距离；n为路径损耗因子，可通过最小均方误 差(minimum mean square error, MMSE)来计算；Xσ为阴影效应，服从高斯分布，均值通常取值为0.n=1时可以理解为一个平面上的导波，n=2等效于自由空间路径损耗，n=4对应天线高度较低导致第一菲涅尔区受阻的情况[16].

与CI对数模型相比，ABG模型支持不同频率，表达式为[17]

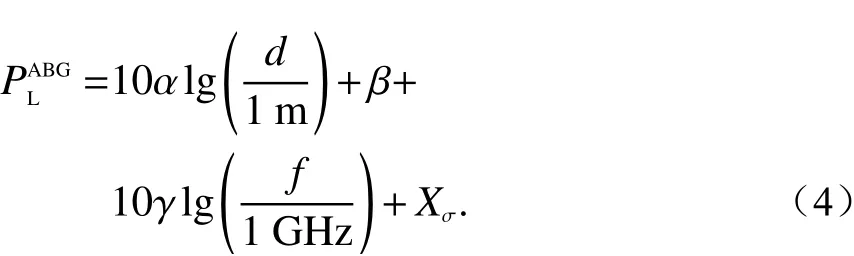
式中：α和γ分别表示路径损耗对距离和频率的依赖关系；β为路径损耗的优化补偿值；Xσ为一个零均值、标准差为σ的高斯随机变量. 采用MMSE来计算各个参数.

当在单一频率下使用时，ABG模型可等效为现有的3GPP浮动截距模型，该模型有三个参数，其中γ参数设置为0或2[18-19].

图4(a)、4(b)分别给出了两种场景中基于自由空间模型、CI对数模型和ABG模型得到的与收发车辆距离相关的所有测量数据接收功率散点图. 模型的拟合参数是全部基于隧道内的接收功率得到的.

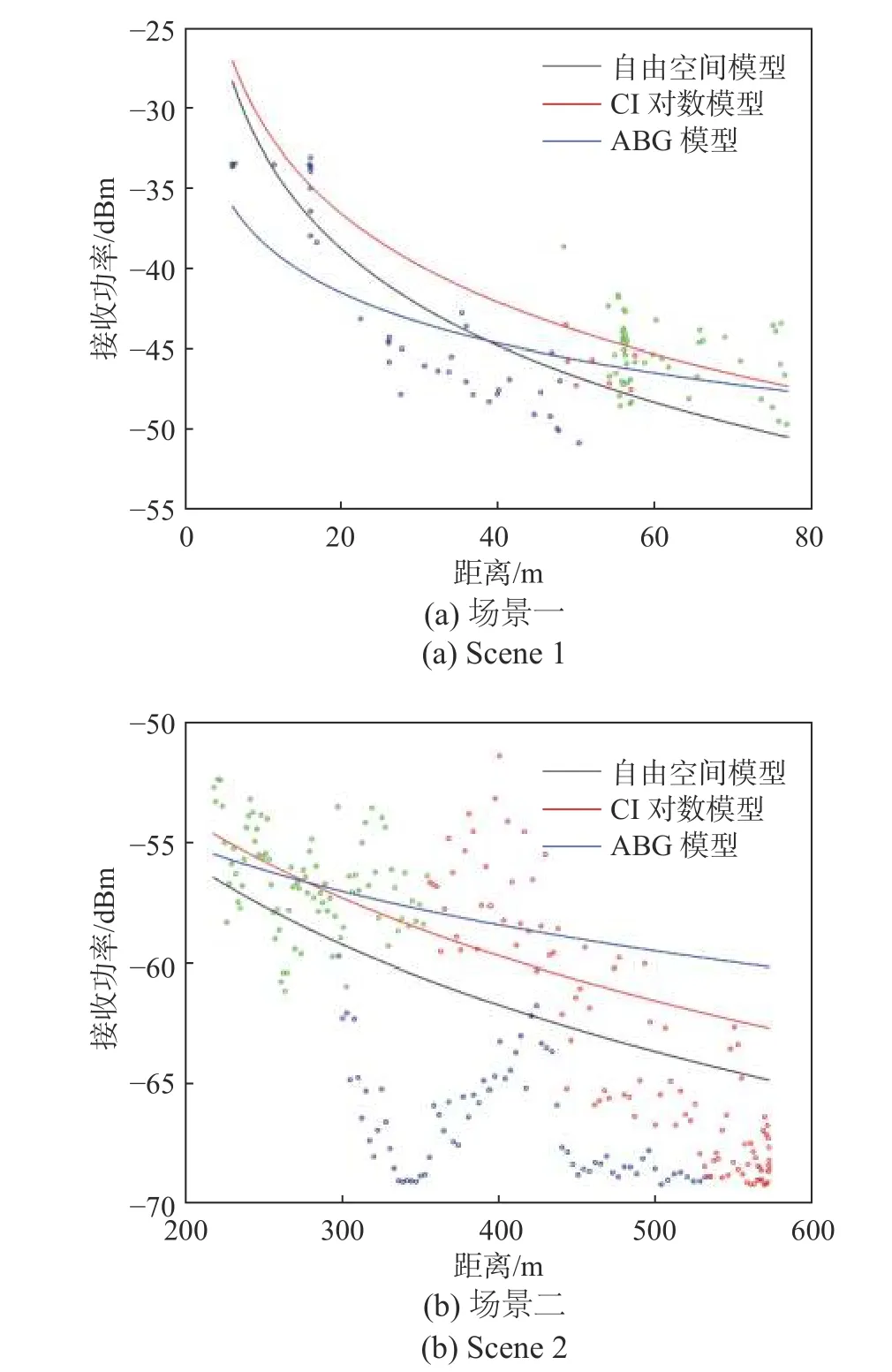
图4 两种场景中三种模型和测量数据的接收功率Fig. 4 Three models and measured data received power in two scenes

从图4可以看到：随着距离的增加接收功率逐渐减小，即路径损耗随距离增加而增加；路径损耗指数越小，接收功率随距离变化的幅度越小. 从表3也可以看到，场景一和场景二中的CI对数模型的损耗因子n分别为1.83和1.9，均低于自由空间中的路径损耗指数(n=2)，这一结果与以前的研究是一致的[20-21]. 这是因为相对于自由空间，隧道环境中两侧和上下的墙体有丰富的反射径，而这些多径分量在隧道环境中有结构的叠加增强了接收点的信号接收功率. 将隧道内测量数据与拟合数据比较，在场景一中，CI对数模型的MMSE为7.14，小于ABG模型的8.55；在场景二中，CI对数模型的MMSE为4.28，小于ABG模型的4.34. 从这些分析可以得出结论：参考距离d0为1 m时，CI对数模型在5.9 GHz和5.2 GHz频率的隧道场景下具有更好的准确性，表明路径损耗最好采用CI对数模型来建模.

表3 损耗模型的参数Tab. 3 Parameters of path loss models

2.2 小尺度衰落分布拟合

为了分析隧道内的信道小尺度衰落特征，首先对接收信号强度进行归一化处理，以减少大尺度衰落效应，即距离相关的路径损耗. 类似于文献[22-25]，使用滑动平均法，利用滑动窗口将大尺度衰落滤除.在滑动窗口长度内，信道被认为是平稳的，即大尺度衰落参数保持不变. 本文根据收发车辆行驶速度和测量间隔，将测量一的窗口长度设置为200个连续测量的CIR快照，测量二的窗口长度设置为300个，以测量一为例得到的隧道内归一化接收功率大小如图5所示.

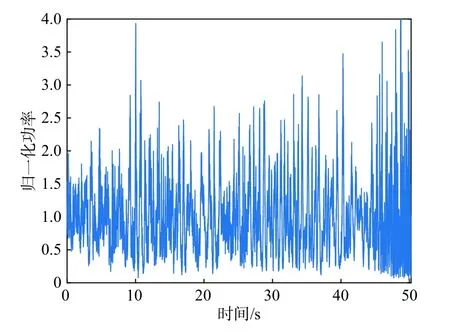
图5 隧道内归一化接收功率Fig. 5 Normalized magnitude of the received signal inside tunnel

测量场景一中，从50 s开始，两辆车均驶入隧道中. 在描述V2V通信信道小尺度衰落的统计特征时，莱斯分布和瑞利分布被经常采用. 另外莱斯分布和威布尔分布已在文章[22]中被使用，当威布尔分布的形状参数k=2时等同于瑞利分布，当形状参数大于2，威布尔分布更接近于莱斯分布. 因此，图6(a)中分别将测量数据幅值统计结果和五种典型理论分布(正态分布、瑞利分布、莱斯分布、威布尔分布和对数正态分布)的累积分布函数(cumulative distribution function, CDF)曲线进行对比.

同样的，对于场景二，从44 s开始两辆车均驶入隧道中，经归一化处理后的测量数据幅值与典型理论分布的CDF拟合曲线如图6(b)所示.

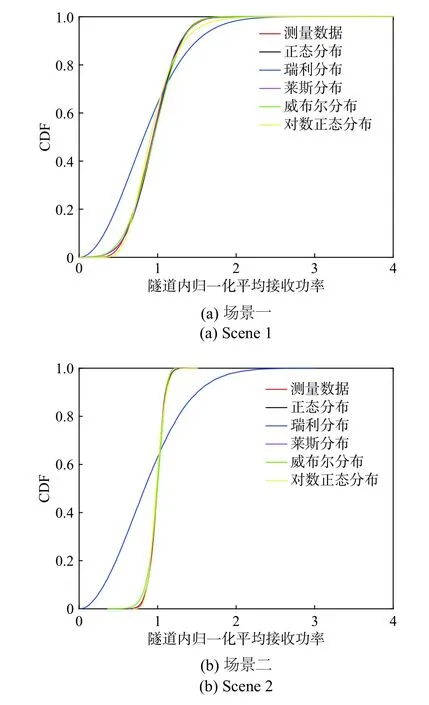
图6 两种场景的CDF拟合分布曲线对比Fig. 6 CDF fitting distribution curve comparison of two scenes

KS(Kolmogorov-Smirnov)检验统计量 ρ作为拟合优度指标[23-25]是描述分布特征的一种主要方法，表达式如下：

式中：suxp 为上限函数；FX(x)和F(x)分别为x的经验和理论CDF. 我们通过统计检验方法分别计算了不同分布的经验和理论CDF之间的 ρ值，其值越低，代表该分布的理论与经验CDF越相近. 表4列出了两种场景中隧道内不同理论分布的拟合优度值指标 ρ.可以看出，每个场景中的正态分布、莱斯分布和威布尔分布的 ρ值非常接近，但莱斯分布的值最小. 考虑到测量时收发车辆距离一般较短，且测量时存在LoS路径，考虑使用莱斯分布来近似隧道内的信道小尺度衰落特征是合理的.

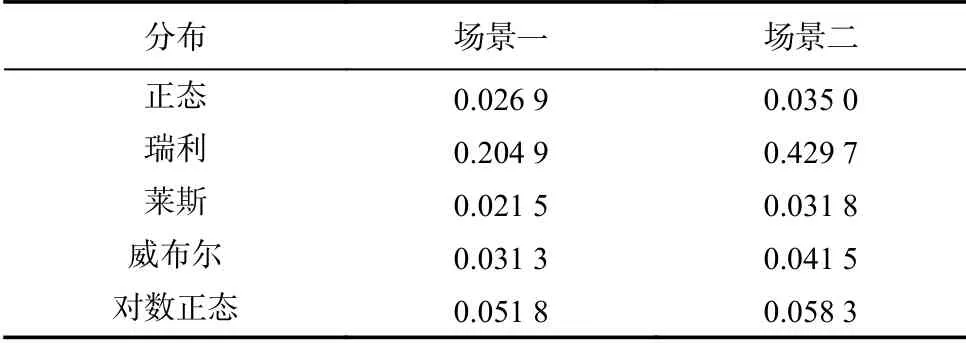
表4 两种场景不同理论分布的拟合优度值Tab. 4 Goodness of fit values of considered distributions

2.3 莱斯K因子

莱斯分布表达式为

式中，Var和E分别代表样本方差和期望估计量. 通常认为样本方差和期望估计值的空间窗口长度必须不超过消除大尺度衰落的窗口长度，因此场景一和场景二分别采用大约180个和250个样本大小的窗口长度来计算K因子.

对于场景一，图7(a)给出了隧道内外和连接处的基于测量数据估计得到的K因子值. 结合图3(a)可以看到：在开始部分，两辆车都是稳定的，距离约6 m，衰落深度是微弱的，LoS情况下的K因子较大；当两辆车开始移动直到收发机之间的距离增加到约56 m时，K因子逐渐降低并达到最低点. 另外，在隧道连接处，K因子也呈现下降的趋势. 在隧道内，由于存在直接的LoS分量，所以K因子值相对较大.K因子的变化可能是由于隧道内环境的变化，例如移动的汽车，导致多径分量的功率变化. 由图7(a)还可以看出，当两辆车都在隧道内移动时，K因子均匀下降，而此时发射机和接收机之间的距离略有增加.因此，得到的K因子与发射机和接收机之间距离具有轻微的相关性，特别是当距离增加时，K因子减小.图8(a)为场景一隧道内外和隧道连接处的K因子随距离变化的情况. 在隧道内，随着距离的增加K因子逐渐减小. 其K因子的均值和标准差分别为7.7和4.3.

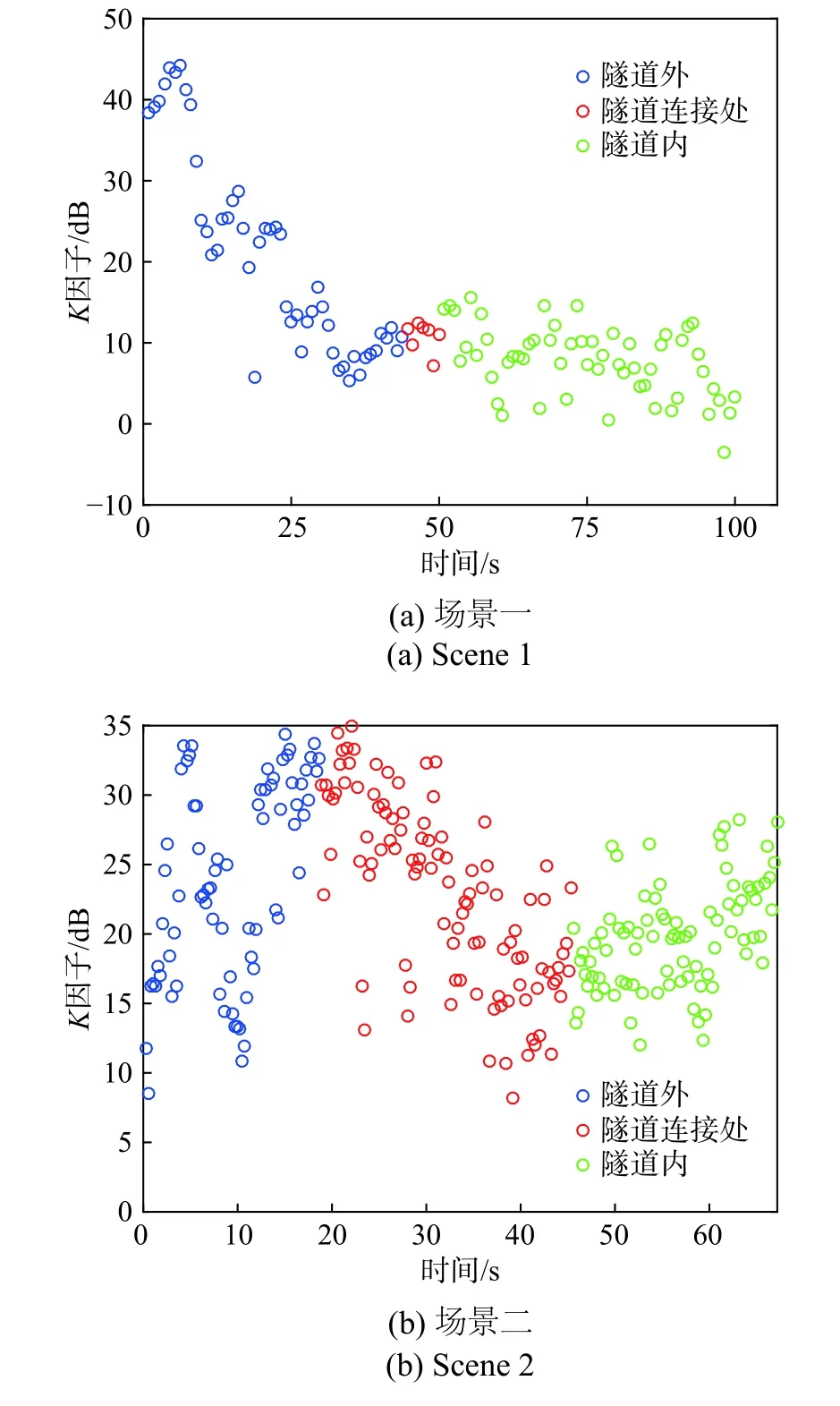
图7 两种场景K因子随时间的变化情况Fig. 7 Variation of the K-factor in two scenes

对于场景二，图7(b)给出了隧道内外和连接处随时间变化的K因子值. 在隧道外，收发车辆的距离逐渐增大，蓝色散点图对应的K因子变化剧烈，可能与行驶过程中多辆高大车辆和地形的遮挡有关，此时K因子的变化与距离没有相关性. 而在隧道连接处，接收机已进入隧道，发射机在隧道外，此时两辆车的相对距离减小，K因子呈下降趋势. 可以看到隧道连接处K因子随着距离的增大而增大，不同于场景一，两种场景呈现相反的表现. 这可能与隧道内接收机接收的多径分量逐渐增加有关，具体在2.4节中分析. 当两辆车都在隧道内移动时，K因子均匀上升.在隧道内，发射机和接受机的距离是逐渐减小的，因此可以看到K因子和收发机的距离也具有相关性.图8(b)给出了场景二隧道内和隧道连接处的K因子随距离变化的情况. 在隧道内，随着距离的增加K因子逐渐减小. 其隧道内K因子的均值和标准差分别为19.4和3.88.

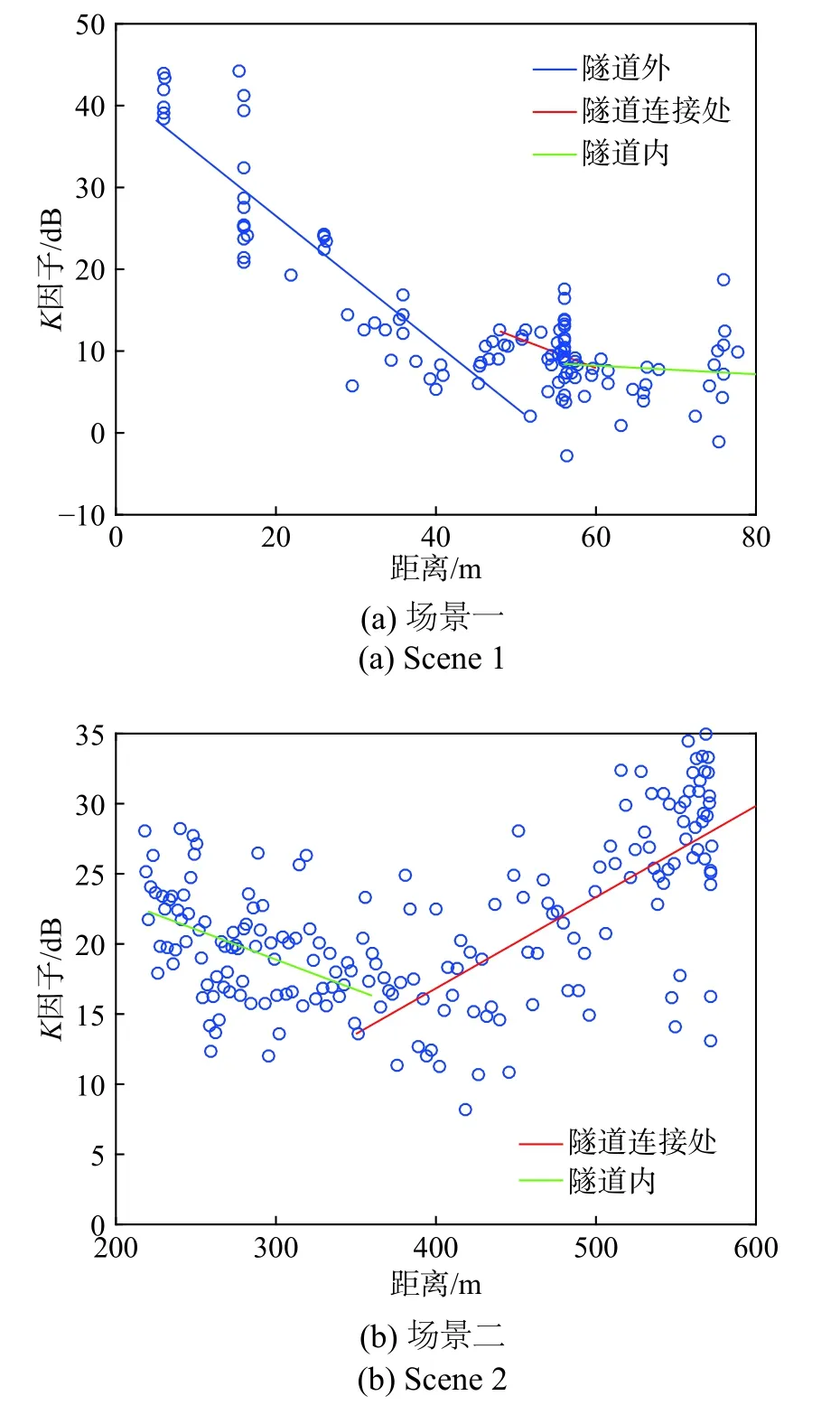
图8 两种场景下基于距离的K因子模型Fig. 8 K-factor model based on distance in two scenes

使用最小二乘法拟合，两种场景中隧道内的基于距离变化的K因子模型可以被定义为

2.4 平均功率时延分布

本节针对两种场景中隧道连接处的信道特征作进一步分析，考虑信道功率时延谱. 功率时延谱能够很好地描述不同多径分量在不同时延上的功率特征，隧道连接处的平均功率时延谱如图9所示，可以看出一直存在一条明显的直射径，在图中显示为明亮的红色. 随着接收机在隧道中行驶时间越长，可以观测到多条平行且弱于直射径的反射径逐渐增强，以及其他一些功率较弱的多径分量以“簇”的形式出现，结合测量场景的周围环境进行分析，这些多径分量是由于周围过往的车辆和隧道壁造成的. 而在两种场景中隧道连接处K因子基于距离呈现相反的情况，K因子随接收机进入时间增长逐渐减小，与距离无依赖关系，很可能是由于多径的增多和增强造成的.

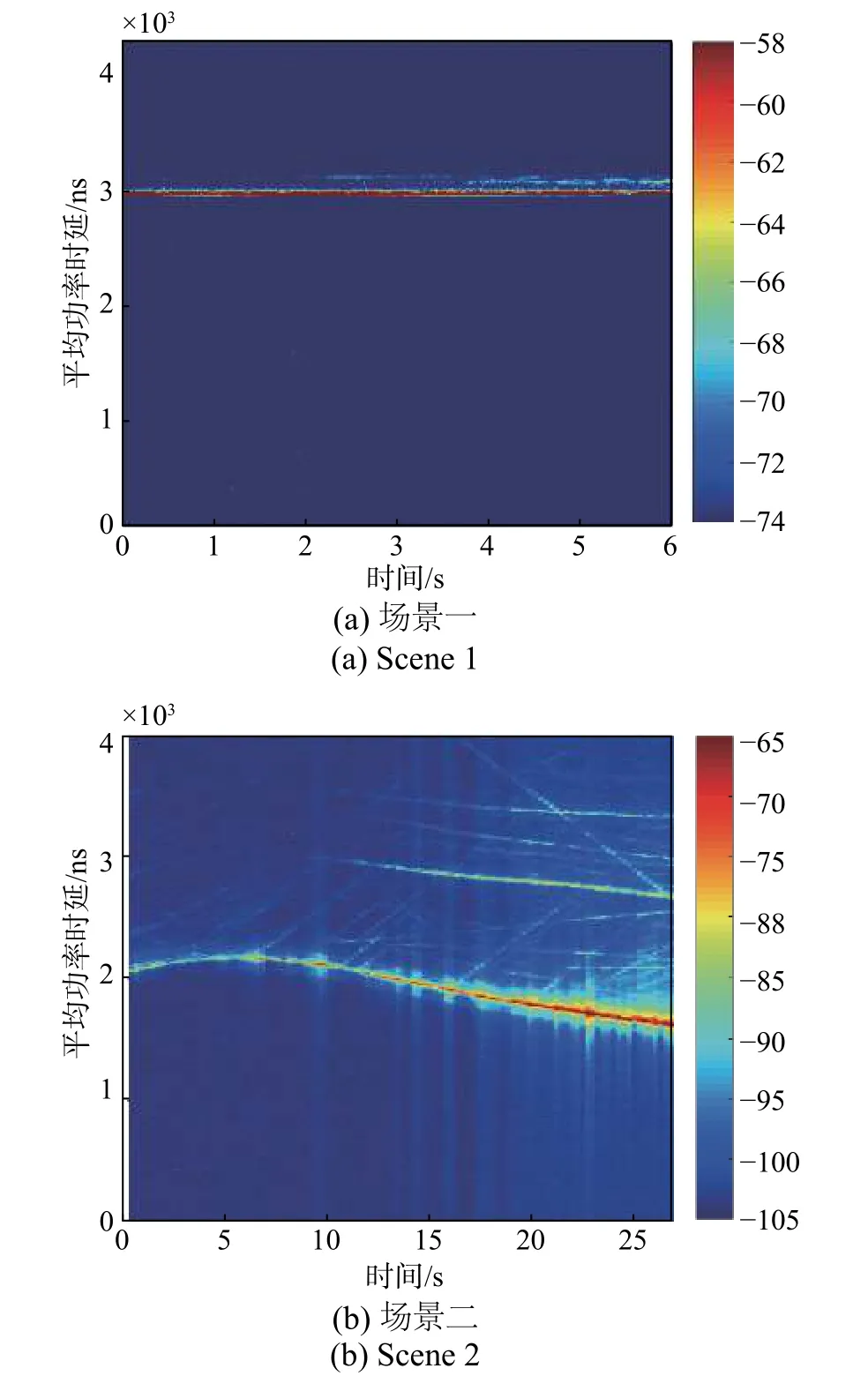
图9 两种场景平均功率时延分布Fig. 9 Average power delay distribution in two scenes

3 结 论

隧道是智能交通系统一个安全要求高的场景.本文在5.9 GHz频段30 MHz带宽以及5.2 GHz 120 MHz带宽条件下分别进行了两次信道测量活动，研究了隧道环境中V2V信道路径损耗和小尺度衰落特征. 首先，5.9 GHz和5.2 GHz两次测量结果均显示，参考距离为1 m的CI对数模型具有相对较高的适用性，其损耗指数分别为1.83和1.9，小于自由空间中的损耗指数. 这意味着随着传播距离的增加，无线电波在隧道中的衰减速度要小于在自由空间中的衰减速度. 其次，由于存在LoS路径，接收到的信号经历莱斯衰落. 场景一中隧道内的K因子的均值和标准差分别为7.7和4.3，场景二中隧道内的K因子均值和标准差分别为19.4和3.88. 此外，在隧道连接处，K因子与距离没有很强的相关，而在隧道内K因子具有一定的距离相关性. 本文提出了隧道内基于距离的K因子模型，当收发机距离增加时，K因子减小. 另外，根据两种场景下隧道衰落特征，针对不同隧道场景开展更多的测量活动和衰落建模，可以更好地了解在恶劣环境下车辆运动、遮挡等情况对无线信道传播特性的影响.

致谢：感谢德国宇航中心的Stephan Sand博士，Paul Unterhuber, Ibrahim Rashdan, Fabian De Ponte Mueller博 士, Benjamin Siebler, Dina Bousdar Ahmed博士，Martin Schmidhammer和Thomas Jost博士对信道测量的协助.