基于振动信号频谱高斯混合模型的 瓷支柱绝缘子故障诊断

焦宗寒 邵鑫明 郑 欣 刘荣海

（1. 云南电网有限责任公司电力科学研究院，昆明 650217；

2. 华北电力大学云南电网公司研究生工作站，昆明 650217； 3. 华北电力大学河北省电力机械装备健康维护与失效预防重点实验室，河北 保定 071003）

0 引言

瓷支柱绝缘子主要用于变电站隔离开关和母线的支撑、固定和绝缘，在实际应用中，若绝缘子出现故障却不能被及时发现，将会造成巨大的经济损失[1-3]。目前瓷支柱绝缘子故障诊断方法有红外测温检测、超声波检测和振动声学检测。红外测温检测只能通过绝缘子表面温度判断绝缘子有无缺陷，无法探测绝缘子内部初期缺陷。超声波检测只能用于非带电检测。振动声学检测方式可以兼顾瓷支柱绝缘子内外缺陷检测和带电检测，具有明显的优势。因此，加强对瓷支柱绝缘子振动信号的研究，提前发现初期缺陷，对变电站运行的可靠性及加强电力系统的稳定性具有重要意义[4-5]。

造成瓷支柱绝缘子故障的原因很多。从内部结构分析，主要是生产制造工艺不合格，如法兰盘与瓷体之间胶状水泥的不均匀性和生产过程中气孔的产生。从外部因素分析，主要是受外部作用力（如风载荷）的影响。通常将瓷支柱绝缘子故障归为绝缘子上端故障和绝缘子下端故障两种[6]。文献[7]提出了对瓷支柱绝缘子振动信号进行小波包分解，对各节点能量进行提取分析的方法，利用瓷支柱绝缘子故障发生前后各小波节点能量的差异实现绝缘子故障判别。文献[8]采用基于统计分布特征的方法，以一定数量瓷支柱绝缘子检测数据的频率为基础直接建立绝缘子的评判标准，证明了振动信号分析的有效性。这些诊断方法仍存在一定的不足，例如，小波包分解求节点能量这一方法只能区分绝缘子的正常和故障状态，无法判断故障位置；而基于统计分布特征的方法主要是通过分析不同状态下瓷支柱绝缘子功率谱密度图的频率区间来判断，因区间范围较宽，故受主观因素影响较大，容易产生绝缘子错检和漏检。

本文将振动信号频谱与高斯混合模型（Gaussian mixture model, GMM）相结合，提出一种应用于瓷支柱绝缘子来提取振动信号特征的新方法，利用粒子群算法（particle swarm optimization, PSO）优化后的极限学习机（extreme learning machine, ELM）实现故障状态识别与分类。针对瓷支柱绝缘子现场数据分析，该方法能快速有效地提取瓷支柱绝缘子的特征向量并能正确地进行状态识别和分类，诊断效果较好。

1 基于振动检测的瓷支柱绝缘子故障识别方法

现有方法通过检测110kV电压等级瓷支柱绝缘子振动的谐振频率来对其进行状态检测，判别步骤为：

1）利用白噪声激励对瓷支柱绝缘子底部的法兰盘进行激励，使其产生激振，然后获取瓷支柱绝缘子振动响应。

2）获取其振动信号的功率谱图。

3）依据功率谱图中的谐振频率偏移方向来判别其故障类型。

2 基于振动信号频谱高斯混合模型的绝缘子诊断相关理论

2.1 高斯混合模型与期望最大值算法

高斯混合模型的主要参数有平均值μ、标准差σ、权重系数α，其中，平均值μ可以反映各频带中心频率位置，标准差σ可以反映频带宽度大小，权重系数α可以用来表示各模态分量所占比重。

假设混合高斯模型由K个单高斯模型组成（即数据包含K个类），则GMM的概率密度函数为[9]

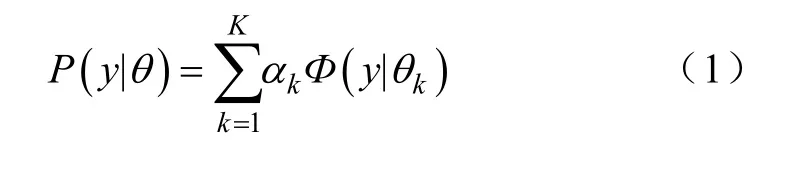
式中：αk≥0是权重系数，是第k个高斯模型的概率密度；的计算如式（2）所示。

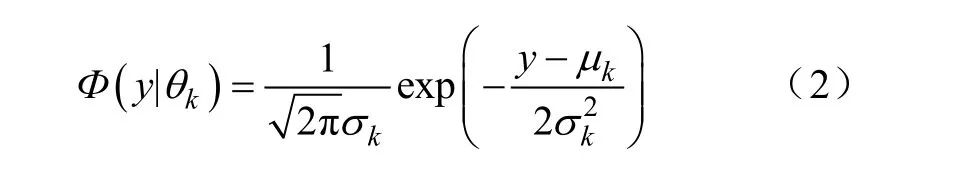
期望最大值算法（expectation maximization algorithm, EM）包括E步和M步。E步，假设参数已知，估计隐藏变量的期望；M步，利用E步得到隐藏变量的期望，根据最大似然估计求得参数，然后将新得到的参数值重新用于E步，直至收敛到局部最优解[10]。

将采集到的瓷支柱绝缘子的振动信号通过快速傅里叶变换（fast Fourier transformation, FFT）将 数据转化到频域内，将频谱样本数据记作y=，通过计算得到参数。

求解GMM的EM算法较为复杂，仅列出求解主要参数的迭代公式（3）。

式中，αm、μm、σm为通过迭代得到的权重系数、平均值、标准差的最大值。

2.2 极限学习机

极限学习机作为单隐层前馈神经网络的一种新型学习算法，只需要设置网络的隐层节点个数，隐含层节点的权重为随机或人为给定，在算法执行过程中不需要调整网络的输入权值及隐元的偏置，并且产生惟一的最优解[11-12]。单隐层神经网络如图1所示。

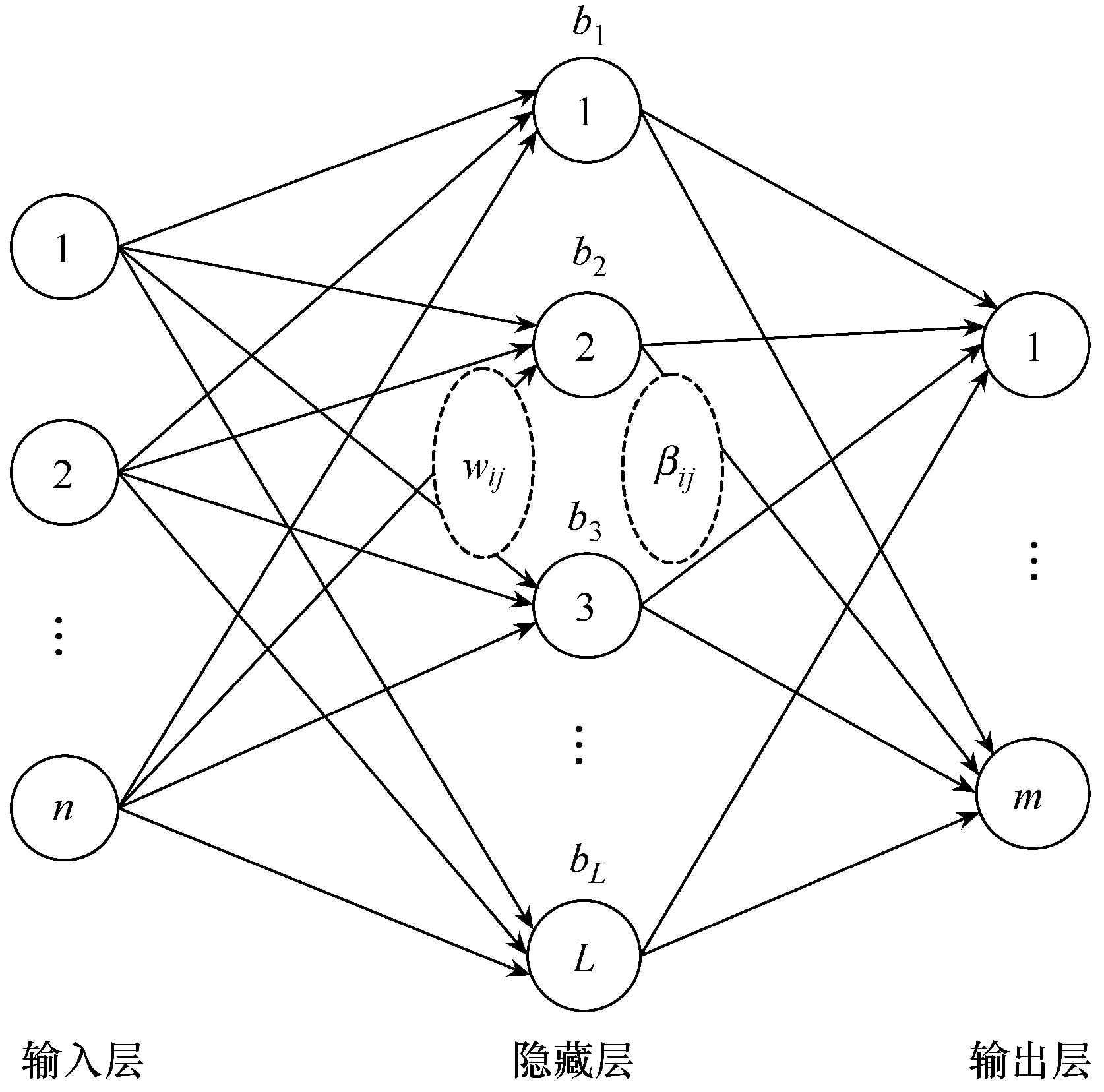
图1 单隐层神经网络

设n、L、m分别为输入层、隐含层和输出层的节点数。给定N组任意样本(xi,ti)∈Rn×Rm，极限学习机算法的求解函数为

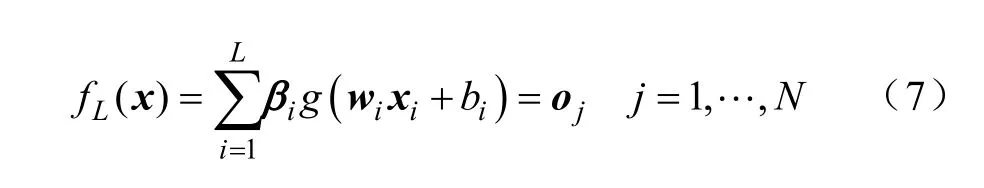
式中：g(x)为激励函数；为隐含层第i个神经元与输入层的连接权值；为隐含层第i个神经元与输出层的连接权值；bi为 第i个隐层节点的偏置；oj为第j个输入样本的输出值。

含有L个隐层节点，且激励函数为g(x)的标准单隐层前馈神经网络可以零误差地逼近N个训练样本，即

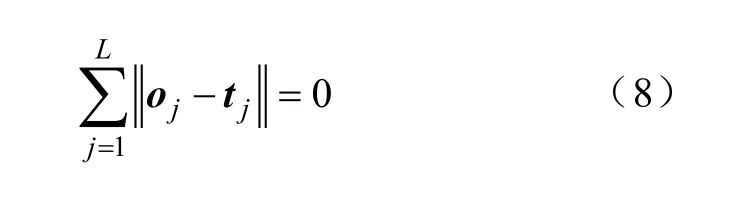
因此存在βi、wi、bi使得

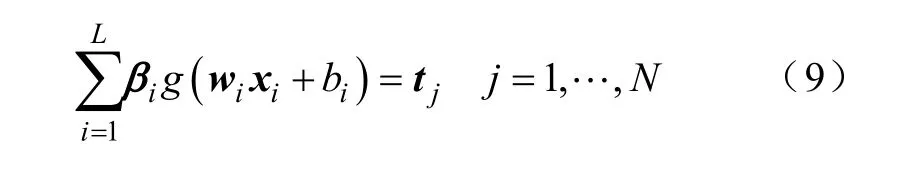
式（9）可表示为

其中

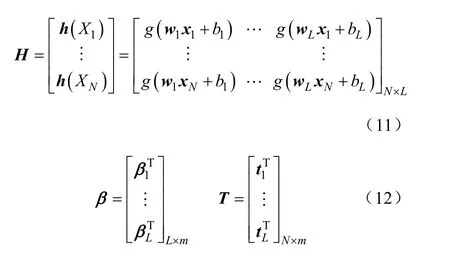
输入连接权值和隐层节点偏置在训练开始时可随机选择，且在训练过程中固定不变。而输出连接权值可通过求解以下线性方程组的最小二乘解来获得[13]，即

其解为

式中，H+为隐含层输出矩阵H的Moore-Penrose广义逆。

通过最小二乘法可以实现对输出层连接权值进行调整，以确定输出最小的偏差和最优的结果。但最小二乘法对样本拟合时，如果函数阶数过小，曲线并不能很好地反映样本点的分布情况，阶数过高时，会出现过拟合。

2.3 粒子群算法

基于极限学习机的不足，通过粒子群算法，可以有效优化ELM网络参数wi和bi，以改善ELM算法输出权值βi不稳定的缺点。

粒子群算法是由Kennedy和Eberhart于1995年提出的，利用群体迭代，使粒子在空间中进行搜索寻找最优解。粒子群算法具有简单易行、收敛速度快、设置参数少等优点，已经成为现代优化方法领域的研究热点[14]。

粒子i的第d维速度更新公式为

粒子i的第d维位置更新公式为

3 基于振动信号频谱高斯混合模型的绝缘子诊断流程

基于振动信号频谱高斯混合模型的绝缘子诊断流程如图2所示。

图2 基于振动信号频谱高斯混合模型的绝缘子诊断流程

4 现场实验

4.1 瓷支柱绝缘子振动信号采集

因变电站瓷支柱绝缘子故障样本较少，本文以云南省玉溪供电局江川变电站306根110kV在役瓷支柱绝缘子和瑞丽变电站77根110kV在役瓷支柱绝缘子作为研究样本。现场瓷支柱绝缘子信号采集如图3所示，采用振动声学检测装置，采集瓷支柱绝缘子的振动信号。该仪器以48kHz的采样频率采集16 384点，单次采样时间约为0.341s。经实验研究与测试表明，该仪器的两个探头抵在瓷支柱绝缘子的下法兰处，能够更好地获取由激振器与法兰面产生的振动信号。

图3 现场瓷支柱绝缘子信号采集

瓷支柱绝缘子裂纹故障常发生的位置是绝缘子的上端和下端。典型的瓷支柱绝缘子振动信号如图4所示。

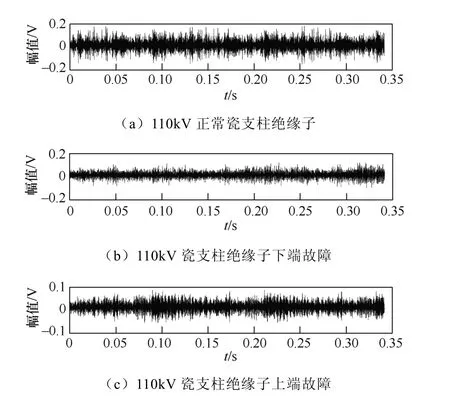
图4 瓷支柱绝缘子振动信号

从图4原始信号时域内观察瓷支柱绝缘子的三种状态，其原始信号较为复杂，没有明显的差异，无法作为故障诊断的依据，因此需从振动信号中提取易于区分的特征用于瓷支柱绝缘子的故障状态识别与分类。

4.2 特征参数提取

首先对变电站瓷支柱绝缘子做快速傅里叶变换，将时域信号转换到频域中，根据瓷支柱绝缘子振动信号的频谱特点预估的模态数K=3，参数初 值随机生成。然后，利用EM算法迭代求得最优参数。最后，分别 用三个高斯概率密度函数将绝缘子三种状态下的频谱图划分成低频模态、中频模态、高频模态三种模态。瓷支柱绝缘子频域高斯混合模型如图5所示。

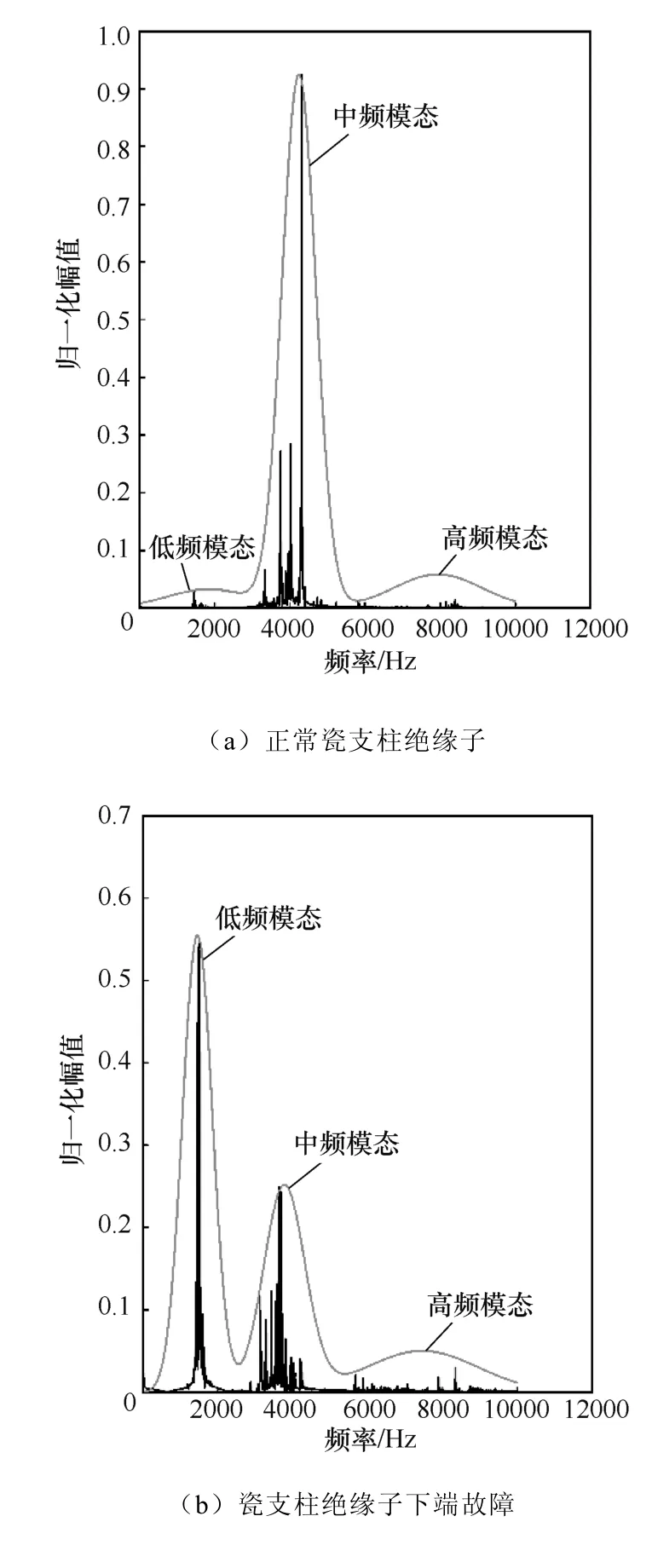
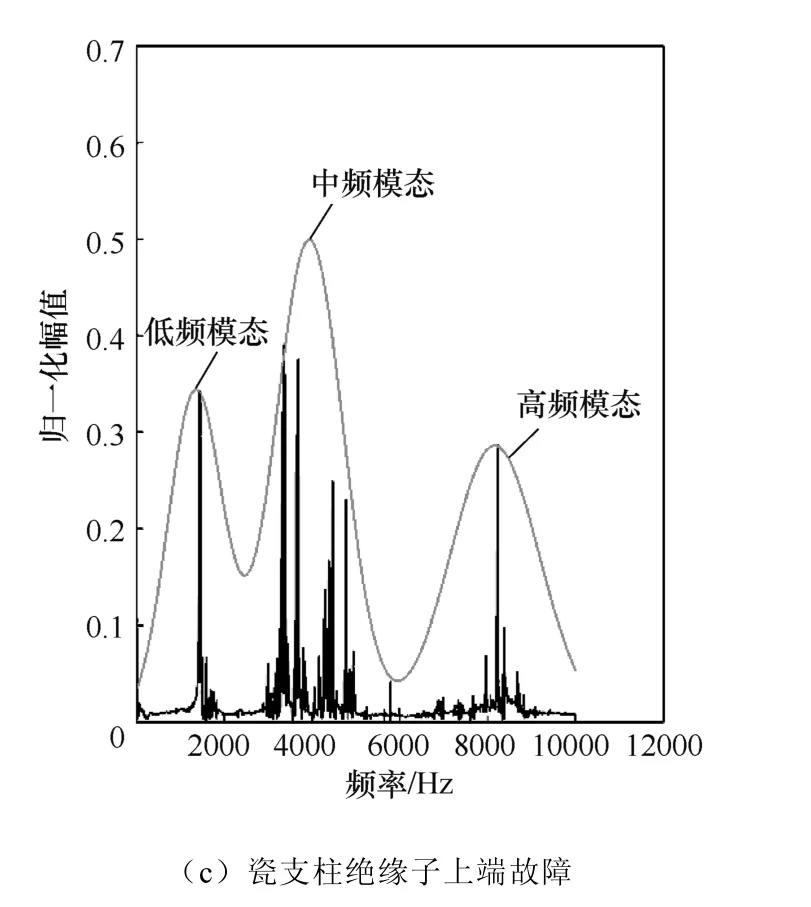
图5 瓷支柱绝缘子频域高斯混合模型

信号的频谱被三个高斯函数分解成低频模态、中频模态、高频模态三个模态，每个模态包括平均值μ、标准差σ、权重系数α三个参数，这三个参数代表了三个特征值，但是平均值μ对应频谱的中心频率在迭代后的位置基本相似，因此平均值μ无法作为故障分类识别的特征。最终，每组信号可提取的有效故障分类特征有六个。在三种状态下各取一组信号，其三种模态下权重系数α和标准差σ分别见表1和表2。

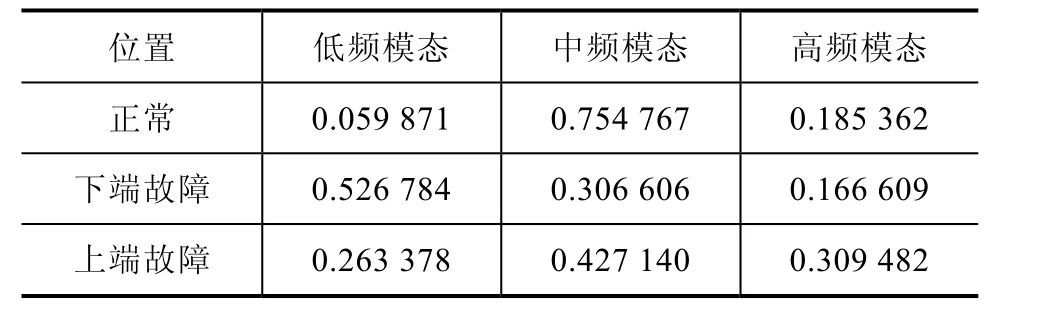
表1 不同状态下三种模态的权重系数α

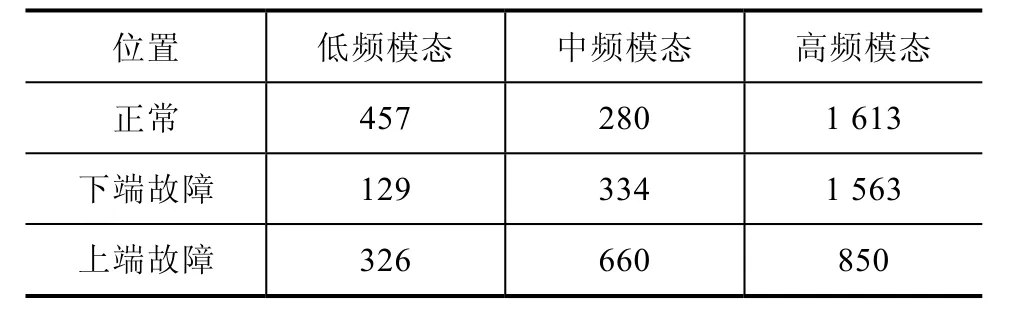
表2 不同状态下三种模态的标准差σ

由表1可知，正常状态下中频模态的权重系数α数值为0.75左右，比低频和高频模态时要高，下端故障时低频模态权重系数α数值为0.52左右，比中频和高频模态时要高，而上端故障时高频模态的权重系数α数值为0.3左右，所占模态比重与正常和下端故障时相比明显升高。

由表2可知，标准差与权重系数相比有一个相反的趋势，正常状态下中频模态的标准差最低，数值为280。下端故障时低频模态的标准差最低，数值为129。上端故障时高频模态的标准差与正常和下端故障时的标准差相比也偏低，数值为850。

不同故障状态下权重系数α和标准差σ在三种模态的数值分布规律性较强，可以作为用于故障分类的有效特征。

4.3 模式识别与分类

从现场采集的三种状态数据中各选取20组，共60组数据，并进行归一化处理。其中45组作为训练样本，15组作为测试样本，引入高斯混合模型并求得不同状态下三种频率模态的权重系数和标准差，作为用于故障分类识别的特征值。

利用标准的ELM构建瓷支柱绝缘子分类模型时，只需要设定隐含层神经元节点个数L和最优的激励函数g(x)就可以得到输出权值矩阵H。但在实际应用中隐含层神经元节点数L往往远小于输入特征值的数目N，当隐含层神经元节点个数L过少时，预测误差会变得比较大，L数目过大则会增加模型预测的时间，容易出现过拟合现象。

在此模型中选用比较常用的sigmoid函数作为激励函数，在确定激励函数之后，用试凑法确定ELM隐含神经元节点个数，确定的方法是通过改变隐藏神经元个数，观察ELM回归模型方均误差（mean square error, MSE）和决定系数R2两个适应度评价指标来确定最优隐含神经元个数、最优输入权值及隐元偏置[15]。经过测试比较之后，设置最优粒子群优化网络参数，种群数目m=40，迭代次数k=100，隐藏神经元个数n=15，学习因子c1=2.8，c2=1.3，惯性权重的搜索范围wmax=0.9，wmin=0.3。对于ELM来说，由于其输入权值及隐元的偏置是随值产生的，g(wL·xN+bL)作为最小二乘法优化的样本点也是不断变化的，最终导致输出权值βi不稳定，容易产生较差的分类效果。PSO可以有效优化ELM网络参数wi和bi，改善ELM算法输出权值βi不稳定的缺点。

图6为ELM和PSO-ELM预测模型的回归曲线，图7为ELM与PSO-ELM分类结果，样本数据分类号1、2、3代表瓷支柱绝缘子的三种状态。

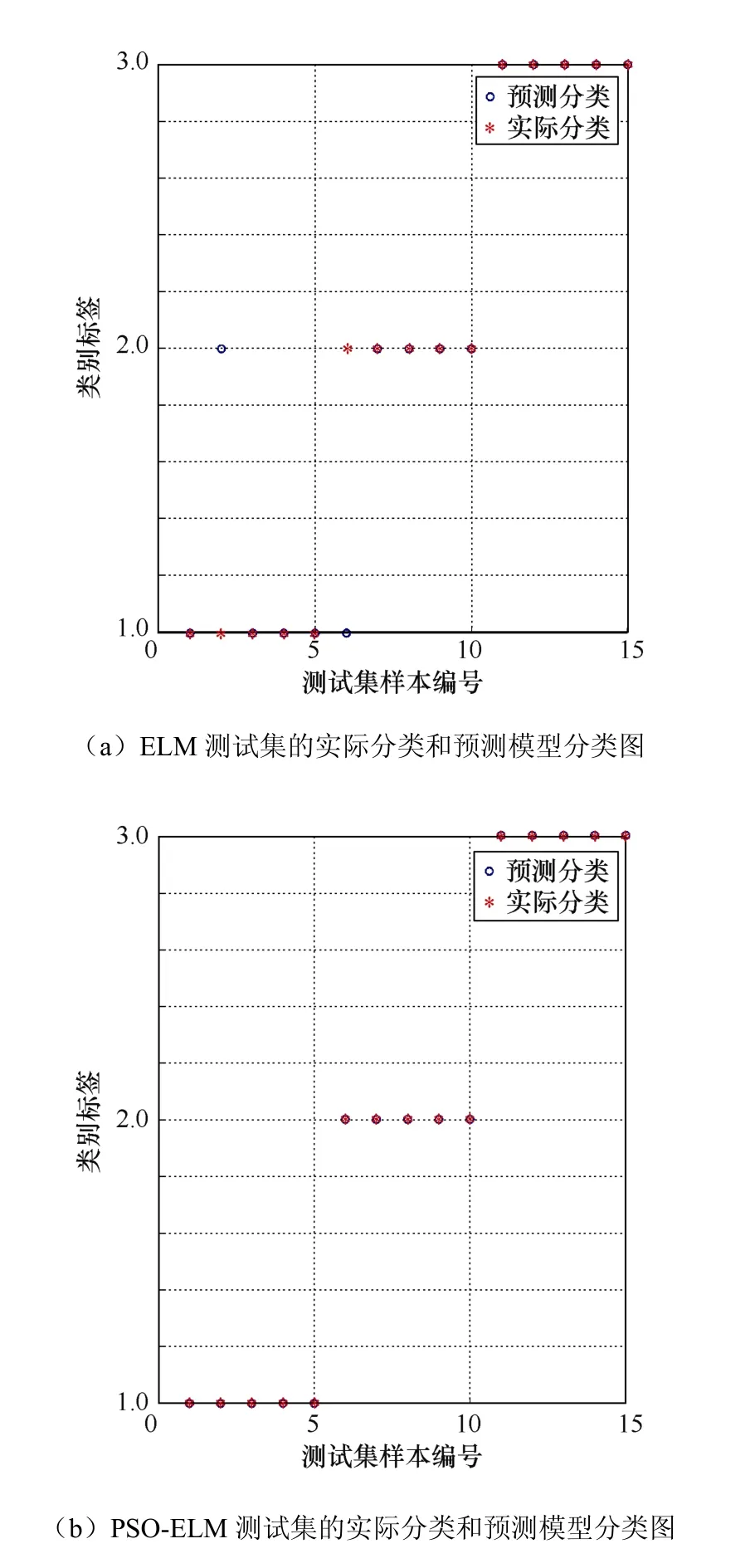
图7 ELM与PSO-ELM分类结果

方均误差和决定系数作为回归模型的评价标准，从图6预测模型的回归曲线来看，PSO-ELM与ELM相比具有更小的方均误差和更大的决定系数，方均误差越小、决定系数越大，则回归模型越稳定。

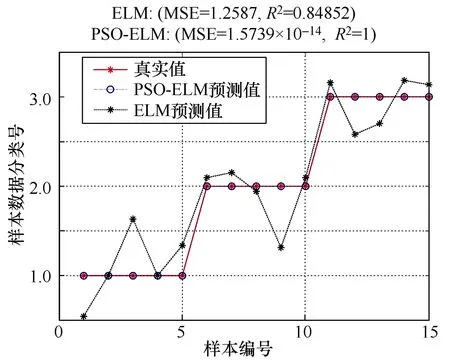
图6 ELM 与PSO-ELM预测模型的回归曲线

图7为ELM与PSO-ELM分类结果，标准的ELM分类正确率为86.7%，而经过PSO优化后的ELM分类正确率可以达到100%。实验结果表明，PSO能够优化ELM模型，得到适应度最高的输入权值、隐元偏置，并提高模型的分类精度，有利于瓷支柱绝缘子故障识别与分类。

5 结论

为了对瓷支柱绝缘子故障进行识别与分类，本文首次采用了振动信号频谱高斯混合模型的方法实现对故障特征的提取。将高斯混合模型中的权重系数α和标准差σ作为用于分类的有效特征值输入PSO-ELM模型中进行状态分类及识别，经研究得出以下结论：

1）通过分析振动信号的特点，将基于概率统计的高斯混合模型与信号频域相结合的方法首次用在瓷支柱绝缘子振动信号分析中，有效提取了瓷支柱绝缘子在三种状态下的特征值。

2）对于故障分类，采用了粒子群优化的极限学习机模型，与未优化的分类模型相比较，PSO-ELM分类模型具有更高的稳定性与识别准确率。

3）本文算法能快速有效地提取瓷支柱绝缘子各状态振动信号的特征值并能正确地进行状态识别和分类，获得了较好的诊断效果，为瓷支柱绝缘子基于振动信号的故障诊断提供了较为实用的解决方案。