空间众包中可拒绝情况下的在线任务分配
2021-07-07林荟荟
林荟荟,黄 杰,李 玉,万 健
(1.浙江科技学院 信息与电子工程学院,杭州 310023;2.杭州电子科技大学 计算机学院,杭州 310018)
随着移动网络的发展和移动设备的普及,空间众包越来越受到人们的关注[1],任务分配问题是空间众包的核心问题[2-4]。目前学术界主要讨论如何将任务高效地分配给任务执行者,同时对其分配的优化目标主要为最大化整体任务分配数量[5-6]。Hien等[7]扩展了分配模型,为每个任务执行者-任务对设置权重,并以最大化总任务分配权重为目标。但是现实中任务执行者和任务是动态变化的,该模型仍然无法实现在整个时间线上最大化任务分配数量的目标。Chen等[8]提出一种基于预测的任务分配算法,然后用贪心算法最大化当前与未来的任务分配数量。但通过采样的方式进行预测,在时间和空间上预测准确度不高。
以上研究都是基于平台分配任务,任务执行者保证执行空间众包任务。但现实中每个任务执行者对任务的选择具有主观性,任务执行者都希望能执行符合他们意愿的任务,比如在自己所处位置附近[9]、任务报酬高[10]的任务,或是与自己的知识、技能相匹配的任务[11]。Zheng等[12]首次定义有拒绝的空间众包问题,提出4种近似分配算法来提高分配的效率,但采用的是静态分配的方法得到最优分配。本研究基于平台分配任务的方式(server assigned tasks,SAT)[13-14]探讨空间众包中任务执行者可拒绝情况下的在线任务分配问题[15],实现提出动态可拒绝的空间众包处理方法:首先最大化任务分配数量,即实现最大匹配;然后,针对任务执行者的主观性,为减少任务执行者拒绝的概率,寻找全局最大匹配下最高兴趣度分配方案。
1 问题定义与处理方法
现有研究[16]已证明空间众包全局最优任务分配是非确定性多项式难题(non-deterministic polynomialhard,NP-hard)。利用批处理模式解决空间众包中任务执行者可拒绝情况下的在线任务分配问题,给定集合p={1,2,3,…}表示整个时间段,其中每个时间片p上存在不同的任务执行者和任务集合,并且在每个时间片内的任务执行者和任务信息均为已知。
1.1 动态移动的任务执行者
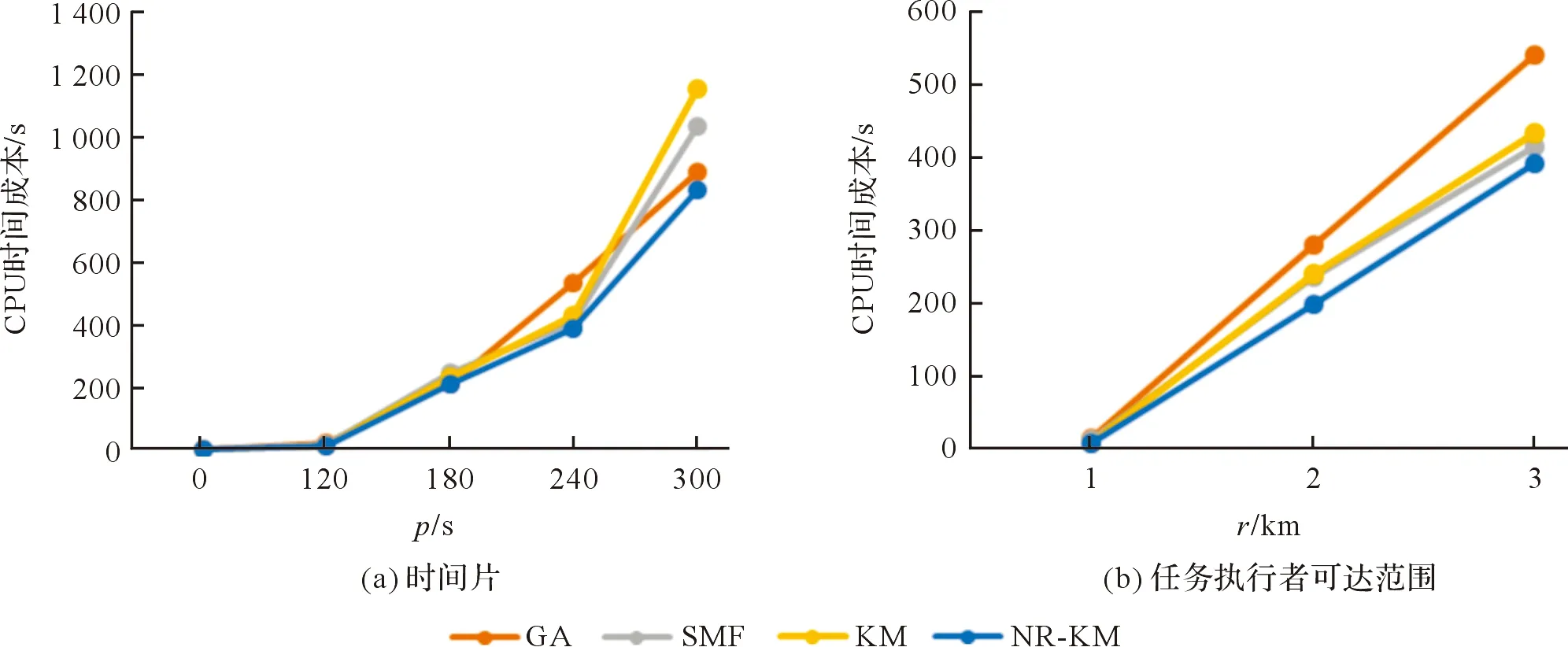
假设集合Wp={w1,w2,…,wm}是在某时间片上m个移动任务执行者的集合,wi∈Wp是其中一名任务执行者,可形式化定义为wi=〈li,pij,ri〉(1 假设集合Tp={t1,t2,…,tn}是在某时间片上n个有时间、位置约束的任务集合,tj∈Tp是其中一个任务,可形式化定义为tj=〈sj,lj,dj,mj,bj〉(1 给定任务执行者集合W和任务集合T,在任意时间片上有m个任务执行者,n个任务。满足时间、空间约束条件下,任务执行者wi对空间任务tj有兴趣,兴趣度权重为pij,任务执行者-任务分布图如图1(a)所示。图1(b)表示任务执行者和任务的待分配情况,每个任务执行者、每个任务表示为二分图中的两边顶点,其中任务执行者和任务的顶点类型不同。任务执行者顶点wi和空间任务顶点tj之间存在一条边,如此,任务执行者-任务对〈wi,tj〉是有效的。 图1 任务执行者-任务分布图和二分图Fig.1 Executor-task distribution and bipartite graph 定义1任务分配数量:在一个时间段内有任务执行者集合W和任务集合T,任务分配策略要求被分配执行的任务数量最大。 定义2任务分配兴趣度:假设任务tj分配给任务执行者wi,则pij为有效分配兴趣度,任务分配策略要求在任务最大化分配的情况下,分配兴趣度最大。 本研究提出的动态可拒绝空间众包处理方法如图2所示。任务执行者和任务动态提交信息至空间众包平台,平台首先划分时间片,查看时间片内的任务与任务执行者是否满足时间和空间约束,为降低任务执行者拒绝的可能性,计算任务执行者-任务对兴趣度,再使用分配算法进行任务分配。若任务分配成功,则将分配策略发送给任务执行者让其执行;若分配失败,当前时间片内未分配任务的执行者和未分配的任务将与下一时间片内任务执行者和任务一起等待下一次任务分配。 图2 动态可拒绝空间众包处理方法Fig.2 Dynamic rejectable spatial crowdsourcing framework 利用主成分分析法(principal components analysis,PCA)[17]预测任务执行者对任务的兴趣度。首先构建兴趣度计算指标体系,将任务执行者和任务之间的距离[18]作为负向指标,将任务移动距离[19]、任务时长[19]、任务价格[20]作为正向指标;然后构建初始化矩阵,归一化处理后得到标准化矩阵;继而计算标准化矩阵得到相关系数矩阵,并计算对应的特征值、特征向量;接着计算每个主成分的方差贡献率,确定主成分个数;最后确定主要评估指标的权重,并进行归一化修正,得到任务执行者对任务的兴趣度。具体计算过程如下: 计算每个主成分的方差贡献率v,va=λa/(λ1+λ2+…+λp),a为正整数,1≤a≤p,va表示第a个主成分的方差贡献率,λa表示第a个主成分对应的特征值。 按照特征值大于1、累计方差贡献率大于指定0.85的原则,提取满足条件的特征值个数作为最终选择的主成分个数;如果满足条件的特征值个数为b,选择b个主成分,λ1,λ2,…,λb为b个主成分分别对应的特征值,其分别对应的特征向量e1,e2,…,eb为b个主成分的特征向量,特征向量和标准化后的数据相乘,得到主成分的线性表达式: Yc=ec1Z1+ec2Z2+…+ecpZp。 (1) 式(1)中:Yc为第c个主成分,c为正整数,1≤c≤b;ecp为某个指标在第c个主成分线性表达式中的系数,表示第c个特征向量中的第p个元素;Zp为第p个指标经过标准化处理后的值。 以主成分的方差贡献率为权重,对主要评估指标在各个主成分线性表达式中的系数进行加权平均,计算每个主要评估指标的综合权重;将所有主要评估指标的综合权重进行归一化,得到每个主要评估指标的权重值w′,w′j表示第j个主要评估指标的综合权重除以所有主要评估指标的综合权重之和,根据获得的权重值进行加权计算,得到每个任务执行者的兴趣度并映射到[0,1]之间。 Hamamda等[21]验证了批处理模式在任务分配上的有效性,故本研究采用批处理的模式解决动态分配问题。 2.2.1 基于MaxFlow的排序算法 采用基于MaxFlow的排序算法(sequence algorithm base on MaxFlow,SMF)求解分配策略。建立一个额外的源点Start和一个额外的汇点End,源点与顶点连接一条容量c为1、权重为0的弧,汇点也执行类似的操作;两边顶点任务执行者wi和任务tj的弧容量c设置为1,权重设置为兴趣度pi,j∈[0,1];完成网络G=(V,E,C,p)构建。 通过增广路算法来求得该网络的最大流量。该算法优点是每次调整流量都遵循最短路径的原则,直到找不到增广路,此时的总流量和兴趣度分数即为所求答案。但是在寻找最大兴趣度增广路的时候需先求出最短路径,已知增流到最后的流量n={min(|Wp|,|Tp|)},针对有多条弧的权重为0的特性,只需对二分图中的权重按照从小到大的顺序排列,再根据排序作为有向路径增流[22]至n值或不存在可增广路为止,如此就找到最小兴趣差最大流路径,转换后也就是找到最大兴趣度最大流路径。 2.2.2 基于KM的不重复构造交替树算法 实际构建二分图的时候,任务执行者与任务数不一定相同。若两边顶点数不一致时,补齐较少边的集合,并将其权重设为0。传统KM算法(Kuhn-Munkres,KM)可求解最大匹配最高兴趣度问题,通过不断修改可行顶标得到相等子图进行增广路探索,直到找到最大匹配为止。一般对其优化都是给每个右顶点加一个“松弛量”函数s,每次开始寻找增广路时初始化为无穷大。在寻找增广路时,检查任务执行者wi和任务tj的边,如果不在相等子图中,让s[j]=min{s[j],lw[i]+lt[j]-p[i][j]}。这样在修改顶标时,取所有不在交错树中的任务集顶点的s值中的最小值作为d值即可。但是每轮匹配过的顶点会被清除,需要重新开始搜索建立交替树。 本文提出基于KM的不重复构造交替树算法(non-repetitive construction of alternating tree algorithm based on KM,NR-KM),在原来树的基础上接着搜索新加入的边。设顶点wi的顶标为lw[i],顶点tj的顶标为lt[j],顶点wi与tj之间的权重为p[i][j]。定义s[i]为原值和lw[i]+lt[j]-p[i][j]的较小值,取所有不在交错树中的s[i]值作为d。每次减掉d后,s变为0的点肯定有新加入的边,所以不重新搜索原来的树,从这些点开始接着原树搜索,直到交错树扩展到存在增广路为止。 使用滴滴盖亚数据计划[23]中西安二环局部区域的滴滴快专车平台的订单司机轨迹数据。在数据中选取的事件发生在东经108.921 859°~109.009 348°,北纬34.204 946°~34.279 936°,轨迹点的采集间隔是2~4 s,轨迹点经过绑路处理,以保证数据都能够对应到实际的道路信息。采用某一天滴滴快专车平台的订单司机轨迹数据,有119 019个订单,共涉及178 56个任务执行者。在试验研究中,由于任务执行者和任务有属性约束,需补充数据集属性。通过原始真实数据集计算出任务时长(unix时间戳形式)、任务移动距离(换算成两地之间的距离);根据滴滴快车订单计价规则,计算任务价格。 试验主要考虑时间片p和任务执行者可达范围r对任务分配算法的影响。时间片范围的设定在一定程度上影响该时间片内任务执行者与任务的数量,间接影响分配结果;任务执行者可达范围直接影响任务能否被任务执行者执行,决定任务执行者-任务有效对的数量,影响分配结果。本研究设置的试验参数见表1(参数数值加粗的为默认值),对每个参数变化的结果都进行50组的试验,取50组试验结果的平均值。所有试验均在一台处理器为Intel(R)Core(TM)i7-7700,CPU为3.60 GHz,内存为16 GB的计算机上进行。 表1 试验参数Table 1 Experimental parameters 为了评估任务分配算法的性能,用3个指标来对比贪心算法(greedy algroithm,GA)、KM算法和我们提出的SMF和NR-KM算法。3个指标为:1)CPU时间成本,即整个时间段内任务分配的CPU时间成本;2)任务分配数量,即整个时间段内任务分配的数量;3)任务分配兴趣度,即在整个时间段内任务分配兴趣度之和。 在默认参数的情况下,4种分配策略的性能比较见表2。GA算法得到整个时间段内分配近似解,没能从全局考虑得到最优解;SMF算法、KM算法和NR-KM算法得到的任务分配数量和兴趣度分数是相同的。NR-KM算法时间效率最优,相比SMF算法速度提高9%,由于重标号每次对一个边进行扫描操作,而SMF算法需要维护标号和队列操作;NR-KM算法因不需要每次重新构建交错树,相比KM算法分配速度平均快11%。 表2 4种分配策略的性能比较Table 2 Performance comparison of four allocation strategies 时间片大小对算法分配时间效率的影响如图3(a)所示,在任务执行者可达范围为默认值的情况下,时间片的大小直接导致任务执行者和任务数量的不同,当时间片较小时,4种算法的分配能力相差不大;但随着时间片的增大,任务执行者和任务数量在一定程度上增多,因此所有算法CPU时间成本增加。任务执行者可达范围对算法分配时间效率的影响如图3(b)所示,在时间片以默认值划分的情况下,当任务执行者可达范围较小时,有效任务执行者-任务对有限,不能体现本文算法的优势;但随着任务执行者可达范围的增大,任务执行者可分配的任务数量增加,相应的所有算法的CPU时间成本都增加,相比之下,本文算法性能最优。 图3 时间片和任务执行者可达范围对算法分配时间效率的影响Fig.3 Effect of time slices and range of executor on allocated time efficiency of NR-KM 时间片和任务执行者可达范围对算法任务分配数量的影响如图4所示,时间片和任务执行者可达范围对算法任务分配兴趣度的影响如图5所示。SMF、KM和NR-KM3种算法分配的结果是一致的,这从侧面反映了算法寻找分配结果的正确性。在时间片比较小或任务执行者可达范围比较小的时候,可供选择的任务-任务执行者分配是有限的,故这3个算法与GA算法得到的任务分配数量与任务分配兴趣度差别不大;但随着时间片和可达范围参数值的增大,逐渐显现出GA算法的劣势。 图4 时间片和任务执行者可达范围对算法任务分配数量的影响Fig.4 Effect of time slices and range of executor on number of tasks assigned efficiency of NR-KM 图5 时间片和任务执行者可达范围对算法任务分配兴趣度的影响Fig.5 Effect of time slices and range of executor on interest of task assignment of NR-KM 本文研究可拒绝情况下空间众包任务在线分配问题,提出动态可拒绝的空间众包处理方法,具有较强的扩展性。为减少任务执行者拒绝的概率,运用PCA方法计算任务执行者对任务的兴趣度;为实现高效、准确的任务分配,提出SMF算法和NR-KM算法寻找最优任务分配方案,并通过试验比较GA、KM、SMF和NR-KM 4种算法的分配性能。试验结果验证了本文算法的有效性,它是一种在任务执行者和任务动态变化情况下的人性化分配。下一步我们将致力于研究不同分配思路和应用场景的在线任务分配算法,以及不同场景下团队合作的空间众包任务分配算法,以更有效地进行任务分配。1.2 有约束的任务
1.3 最大匹配下最高兴趣度问题

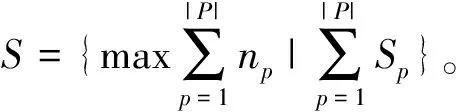
1.4 动态可拒绝的空间众包处理方法

2 动态可拒绝的空间众包分配方法
2.1 兴趣度预测
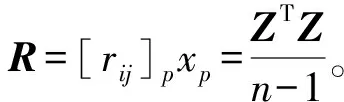
2.2 动态分配算法
3 试验结果与分析




4 结 语
