基于HSV彩色空间与改进OTSU的车位线分割方法
2021-07-07陈雷雷赵国庆暴佳伟
陈雷雷,赵国庆,暴佳伟
(北京石油化工学院信息工程学院,北京102617)
随着现代智能交通系统的发展,车位线分割成为智能交通的热门研究方向,同时也是智能化泊车的关键技术和难点之一。目前,应用最广泛的是基于超声波雷达传感器的车位线检测和定位。但相对于超声波雷达车位感知系统,基于机器视觉的车位感知系统不要求相邻车位有其他车辆停靠或其他可定位反射的物体[1-3],还可以获得更多的车位信息,扩大了智能化泊车系统的适用范围。随着计算机软硬件技术的飞速发展,图像处理技术已经被广泛地应用于生活的各个领域,促使机器视觉的车位线检测和定位成为新的热门研究方向,为后续路线规划和车辆控制提供新的信息获取途径[4]。目前,基于机器视觉的车位线分割方法主要分为以下2类:
基于RGB色彩空间的车位线识别算法,朱旺旺[5]、胡振等[6]将获取的RGB彩色图像直接转换为灰度图像,去噪并二值化后再进行形态学处理和边缘检测等步骤,提取出车位线区域。该方法能够有效找到包含车位线的区域,节省时间,满足实时性要求,但实际上完全忽略了利用车位线的颜色信息,同时受背景和光照干扰的影响较大,往往最后检测到的车位线非目标信息较多,使定位准确度大大下降。
基于形状的检测方法是利用车位线的形状信息,主要有模板匹配法、Hough变换法等[7]。胡振等[6]利用模板匹配法对车位线进行匹配识别,但是不具有旋转不变性和尺度不变性,匹配的效果较差,有一定的局限性。Hough变换抗噪效果好,对简单图形有很好的检测效果,但对复杂的图形检测效果会变差,检测后往往存在大量无效信息。
针对目前车位线分割方法存在的问题,笔者提出基于HSV色彩空间与改进OTSU分割算法的车位线分割方法。李磊等[7]研究表明,在光照不均匀以及存在阴影等情况下,HSV彩色空间的H阈值信息同样得到较好的预期分割效果。因此,选择HSV色彩空间可以有效避免RGB色彩空间易受外部光照变化的影响。经过改进的OTSU算法大大缩短了图像分割需要的时间,减少了计算量,弥补分割时间较长的不足。该分割方法首先将图像的RGB色彩空间转换成HSV色彩空间,利用先验知识,车位线(黄色)在一定色相范围内,依据HSV色彩空间将RGB空间中相关性很强的R、G、B值转化为相关性较弱的H、S、V值的特点[8],可以对非目标像素进行初步的过滤。然后,利用H分量、S分量与改进OTSU算法相结合的方法进一步对非目标像素过滤,分割提取出目标区域。最后,将提取的目标区域进行二值化处理,再利用形态学和Hough变换结合的方法,最终获得一个比较完善的车位线信息。
1 总体设计
整体思路是利用爬虫技术在网上获取车位线图像,先进行数据清洗获得具有代表的车位线图像。对分割的图像先从RGB空间转化为HSV空间,结合H分量、S分量与改进的Otsu算法对非目标像素过滤,分割出目标区域,最后利用形态学与Hough变换结合的方法处理,获得一个比较完善的车位线信息。整体流程如图1所示。

图1 整体流程图
2 彩色空间模型
2.1 RGB、HSV彩色空间
RGB色彩空间是目前运用最广的颜色空间之一,其建立在1个单位长度的立方体笛卡尔坐标系中,3个分量分别为R(红)、G(绿)、B(蓝),通过3通道颜色的相互叠加得到多样的颜色,RGB彩色空间可以定义为:
O(x,y)=[R(x,y),G(x,y),B(x,y)]T=
(R,G,B)T
(1)
RGB色彩空间是一种常见的颜色表示法,但RGB空间内的任意一色彩都是通过R、G、B3个分量的共同作用,3个分量相关性很高,无法用单一的参数进行数字化调整。然而,HSV彩色空间3个通道没有必然的联系[8],更有利于对各个分量进行操作而不影响最后效果,且车位线有明显的色相信息,有利于车位线的提取。因此,引入了HSV彩色空间。
HSV颜色空间更适合人类视觉颜色空间,由色调H(Hue)、饱和度S(Saturation)和亮度V(Value)3个分量组成[9]。其中H表示不同的颜色,S表示颜色的深浅,V表示颜色的明暗程度。
2.2 RGB转化为HSV空间
从RGB到HSV的转换是一个简单的非线性变换[10]。RGB空间到HSV空间的量化过程:
Step1: 对RGB进行归一化处理:
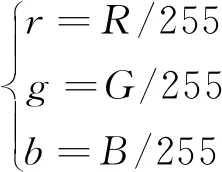
(2)
设(r、g、b)为RGB空间的1个点,归一化后,其为[0,1]之间的实数,减少计算的复杂度。
Step2: 从RGB色彩空间到HSV色彩空间进行转换:

(3)
S=

(4)
V=max
(5)
其中:max为r、g、b中的最大值;min为其最小值。
H分量值规范化在0~360之间,S分量规范化在0~255之间,但在计算机数值计算时,会将H、S归一化为[0,1]之间的实数。
选择HSV色彩空间作为待分割的彩色图像的色彩空间,原图像以及其HSV空间的各个分量图如图2所示,用灰度图像的形式表示,从图2(b)和图2(c)对比观察可以发现,在局部颜色相同的图像区域(车位线区域),其色相值一致性很高,非常便于图像分割。

图2 车位彩色图像及其在HSV各个分量图
3 OTSU及改进型算法
3.1 传统的OTSU算法
最大类间法又名大津法,是由日本学者大津提出来的。其思想是按图像的灰色特性将图像分为目标部分和背景部分,通过计算比较背景和目标之间灰度值的方差来找到最佳阈值,方差差距越大图像两部分差距就越大,使得方差最大的灰度值即为最佳阈值[11],从而达到图像分割的目的。设灰度图像灰度值为H个,则一幅图像的灰度取值范围在[0,H-1]。
计算两类G0和G1的类间方差:
ε(t)=ω0(υ0-υ)2+ω1(υ1-υ)2=
ω0ω1(υ0-υ1)2
(6)
最佳阈值为:
T=max(ε(t))
(7)
G0和G1两类像素的个数在整体图像中所占的百分比分别为ω0、ω1,两类灰度均值分别为υ0、υ1。在[0,H-1]范围内,改变t的值,找到其中方差值最大的值T,即为最佳分割阈值。由上述算法可知,需要将每一个灰度值作为阈值,通过上述算法计算得到方差进行比较,过程计算量比较大,导致分割时间较长,不能满足实时性的要求。
3.2 粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是一种群智能算法,是由J.KENNEDY和R.C.EBERHART提出的[12],其基本思想是通过粒子个体的简单行为、群体内的信息交互寻求全局最优。该算法操作简单、收敛速度快、求解精度高、易于实现。
粒子的速度以及位置是根据其本身的经验以及同伴的经验进行动态调整,主要公式如下:
粒子i的第d维速度更新式为:
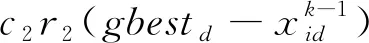
(8)
粒子i的第d维位置更新式为:

(9)

3.3 骨干粒子群优化算法
Clerc和Kennedy通过对粒子运动轨迹分析,证明标准的粒子种群算法中的粒子都是向着其个体最优位置和群体搜索到的全局最优位置的加权位置收敛[13]。
依据以上结论,Kennedy于2003年提出了标准粒子群算法的一个简洁版本BPSO算法[13],与标准的粒子群算法相比,去除了惯性权重w、速度v和加速度常数c1、c2等参数。由于其简单无参数、易于实现、收敛速度快等优点,被广泛应用于求解静态优化问题。BPSO算法中的粒子的位置由高斯采样直接获取,具体更新式为:

(10)
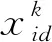
3.4 改进的Otsu算法
改进的Otsu算法是在传统的Otsu基础上,通过粒子群优化算法对其计算进行优化[14-15]。主要思路是将Otsu算法与粒子群算法结合,将Otsu算法作为粒子群算法的适应值函数(fitness function),来计算每个粒子的适应度与最优阈值比较,经过多次迭代最后取得优化后的阈值。
通过优化前的Otsu算法与PSO算法以及BPSO算法优化后的Otsu算法进行比较,主要通过迭代次数、运行时间、最佳阈值的比较等多个性能指标进行验证,来判断改进的算法是否达到预期的目标。
基于PSO改进的Otsu分割算法的综合思路如下:
Step1:将Otsu算法求类间方差的公式(6)作为粒子群优化算法的适应值函数;
Step2:以当前计算的分割阈值作为粒子的当前位置,以阈值的更新速度作为粒子的当前速度;
Step3:利用先验知识,调整w控制粒子对当前速度的继承比例,从而实现全局搜索和局部搜索的平衡;
Step4:根据更新的每个个体、每个种群的最优位置,在灰度空间动态搜索类间方差最大阈值,并记录运行时间、迭代次数等性能指标。
其中,BPSO算法是进一步优化PSO算法,去除了惯性权重w、速度v和加速度常数c1、c2等参数。BPOS算法中的粒子的位置由高斯采样直接获取,根据式(10)更新种群中所有的粒子下一代的位置,除去粒子越界因素,计算所有粒子的适应值,根据更新的每个个体、每个种群的最优位置,在灰度空间动态搜索类间方差最大阈值,并记录运行时间、迭代次数等性能指标。
4 车位线的分割
4.1 图像预处理
在车位线图像中,车位线的目标灰度级比较高,而且往往车位线所占整个图像的比例较小,两者面积相差太大时很可能导致最佳阈值偏移到背景区域,将部分背景也分割到目标区域里。因此,可以根据车位线(黄色)在一定色相范围内,依据HSV色彩空间H、S、V3个分量间的相关性弱的特点,先将色相有效范围之外的像素点去掉(用黑色像素代替)可以对非目标像素进行初步的过滤,有效地避免改进的Otsu分割过程出现的漏检 (把目标类的像素错分为背景类)的情况[16]。
车位线彩色原图、预处理图和处理后的HSV空间分布如图3所示。由图3(a)中可以看出,原图中具有相对较好的车位线信息,也具有黄色广告牌以及黄绿色的草木作为干扰信息,采用此图作为分割算法的测试图具有一定的代表性。根据国家标准 GB5768.3—2009[17]及推荐性国标 GB/T16311—2009[18],结合一般经验,车位线为6~10 cm的黄色标线。黄色车位线在图像中的色相在[20,80]的范围内,但考虑到实际环境中车位线磨损情况,色相范围适当地扩大为[15,85],即色相归一化值在[0.042,0.236]内的像素包含了目标车位线的像素,处理结果如图3所示。

图3 车位线彩色原图、预处理图和处理后的HSV空间分布
利用色相范围有效地将非目标的像素进行初步的过滤。从图3(c)、图3(d)中可以看出,大部分非目标像素点已经被过滤。其中,一部分区域是广告牌和车位线,颜色非常接近,一部分绿色的植物没有过滤掉,门口台阶灰色部分由式(3)可知,色相的取值在于r、g、b3个值任意2个的差值和另外2个的差值之商,而此时r、g、b3个值非常接近时,饱和度S趋近于0,色相没有任何意义,因此没有过滤掉。
为了将黄色部分的车位线分割出来,从图3(d)中可以看出,目标像素在H与S极坐标系中聚合度很高,可以利用聚类的方法将目标像素分割出来,但在聚类过程中为了很好地将目标像素与其余像素区分,需要进行大量的计算,从而导致效率不高,在加上H、S、V分量之间没有必然的关联,利用逐一对H、S分量进行过滤处理的方法,既降低了维度,又有效地减少计算量。
4.2 H分量过滤
根据上文分析并结合图3(b)中H分量的直方图可以看出,直方图存在明显的波峰和波谷, 因此利用改进的Otsu算法选择合适的阈值将非目标像素进一步去除,预处理图和处理后的H分量图如图4所示。 从图3(c)以及图4(a)中可以看出,车位线区域存在很多孤立的小点(即噪声),这些小点与车位线区域的灰度值相差较大,可以先对H分量图像去噪处理。中值滤波是一种非线性处理技术,主要功能就是将周围像素之间的灰度值差异较大的像素修改为与周围像素接近的值,从而消除孤立的噪声点并有效地抑制图像中的噪声[19]。因此,得到预处理图像的H分量图像后,先对其进行中值滤波处理以滤除图像中的噪声,再进行H分量非车位线的过滤,处理结果如图4所示。

图4 预处理图和处理后的H分量图像
由图4(c)中可以看出,彩色图像在色相空间的分割结果有效地说明了H分量的像素点聚合度很高,此时从图4(d)可以看出,门口台阶区域以及植物部分区域b非目标像素已被过滤,符合目标信息进一步分割要求。
西方园林最早可以追溯到古埃及时期,当时是为了农事耕种的需要。从古埃及的宅园到中世纪的庭园,其间经过古希腊、古罗马园林,是规则式园林的发展阶段。文艺复兴运动将欧洲园林艺术带入了新的一个发展阶段,法国的古典主义更是使欧洲的规则式园林艺术达到不可逾越的高峰,由勒诺特尔设计的凡尔赛宫便是在此时产生。凡尔赛宫虽是皇家园林,但法国不像中国有着专制主义中央集权的传统。法国是15世纪末到16世纪初才形成中央集权国家。17世纪中叶,法国的君主专制制度达到顶峰,路易十四登上王位,君主权利高度集中,凡尔赛宫就是在法国君主专制达到顶峰时的产物。与中国不同的是,凡尔赛宫除了是一座皇家园林外,还承担了皇室宫殿的功能。
4.3 S分量过滤
根据H分量过滤处理结果可以看出,部分区域还存在非车位线信息,结合图4(d)可以明显地看出,这部分信息基本分布在低饱和度区域,即a所指区域。根据改进的Otsu算法获取S分量的分割阈值,将饱和度低的部分进行过滤。再加上H分量的进一步过滤,图像的总像素个数再一次下降,进一步减少了计算量。处理前、后的图像以及S分量的直方图如图5所示。

图5 S分量过滤前后的分割结果
从图5中可以看出,分割效果良好,车位线信息被完整地分割出来。但广告牌部分没有分割,主要原因是其与车位线的颜色接近,色相与饱和度相差不大,没有过滤掉。此时可以结合形态学以及Hough变换方式将其过滤,提取车位线。
4.4 形态学处理以及Hough变换
形态学即数字形态学(Mathematical Morphology),是图像处理中应用最为广泛的技术之一。由图5分割结果可以看出,车位线轮廓有小的间隙,可以利用形态学方法中的开运算进行进一步的优化处理[20-21],为了消除剩余的非车位线信息,可以利用Hough变换法通过对车位线的检测方式将其过滤[22-23],得到一个比较完善的车位线轮廓。
开运算是先膨胀后腐蚀可以使轮廓变得光滑,通常可以弥合狭窄的间隙,填充小的空洞。
图像g(x,y)被结构元素B腐蚀,定义为:
(g⊖B)(x,y)=
min{g(x-t,y-s)-
B(t,s)|(x-t,y-s)∈Dg;
(t,s)∈DB}
图像g(x,y)被结构元素B膨胀,定义为:
(g⊕B)(x,y)=
max{g(x-t,y-s)+
B(t,s)|(x-t,y-s)∈Dg;
(t,s)∈DB}
Hough变换是图像处理中从图像中识别几何形状的基本方法之一。车位线部分有很多狭窄的间隙,对Hough变换检测直线过程造成一定的干扰,使得检测结果不理想。所以先对S分量分割后的图像进行形态学的膨胀操作弥补车位线的间隙,再进行Hough对车位线(四边形)进行检测,提取出车位线轮廓,将不符合的像素过滤,最后对处理后的图像进行腐蚀操作。处理结果如图6所示。

图6 S分量过滤后以及形态学Hough变换处理结果
从图6中可以看出,形态学与Hough结合处理结果将车位线间隙进行了填充,也将非目标信息进行最后的过滤处理,最终得到一个比较完善的车位线轮廓。
5 实验结果及分析
在PC端使用MathWorks公司出品的Matlab软件(版本R2012b)进行编码,以JetBrains公司出品的PyCharm(版本2019.3)智能开发集成工具为辅助,利用各100张相对单一和相对复杂环境的具有代表的车位线图像测试数据,主要通过迭代次数、运行时间、最佳阈值的比较等多个性能指标进行验证来判断改进的算法是否达到预期的目标。提取结果分别如图7~图9所示,车位线分割结果分别如表1、表2所示。
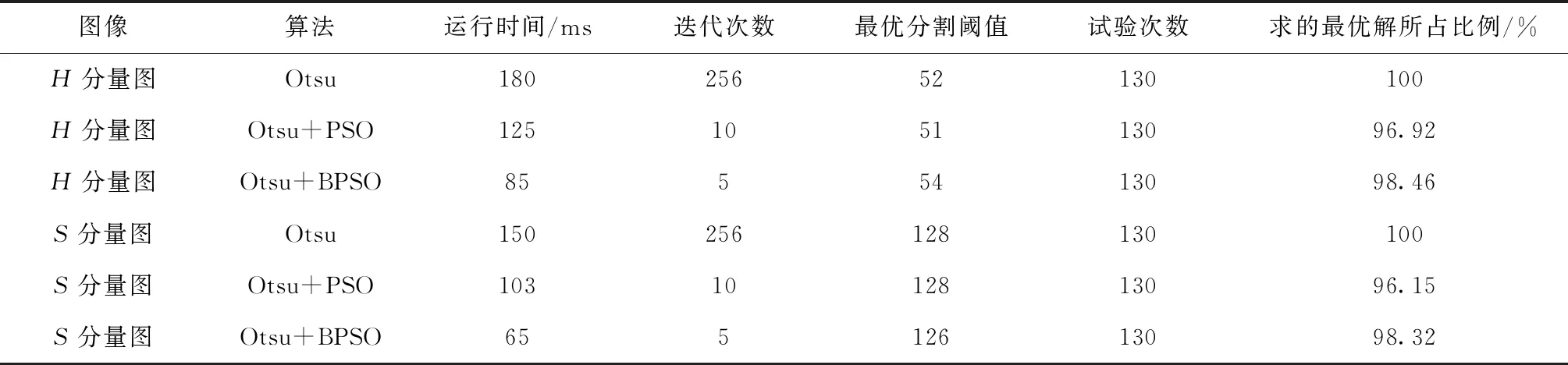
表1 相对单一的车位线分割结果对比

表2 相对复杂的车位线分割结果对比
从图7~图9中可以看出,基于HSV空间分量的分割效果比RGB空间分割效果要好。另外,加上图像预处理以及HSV空间分层依次过滤,图像的总像素点不断减少,进一步减少了计算量,提高了分割效率。
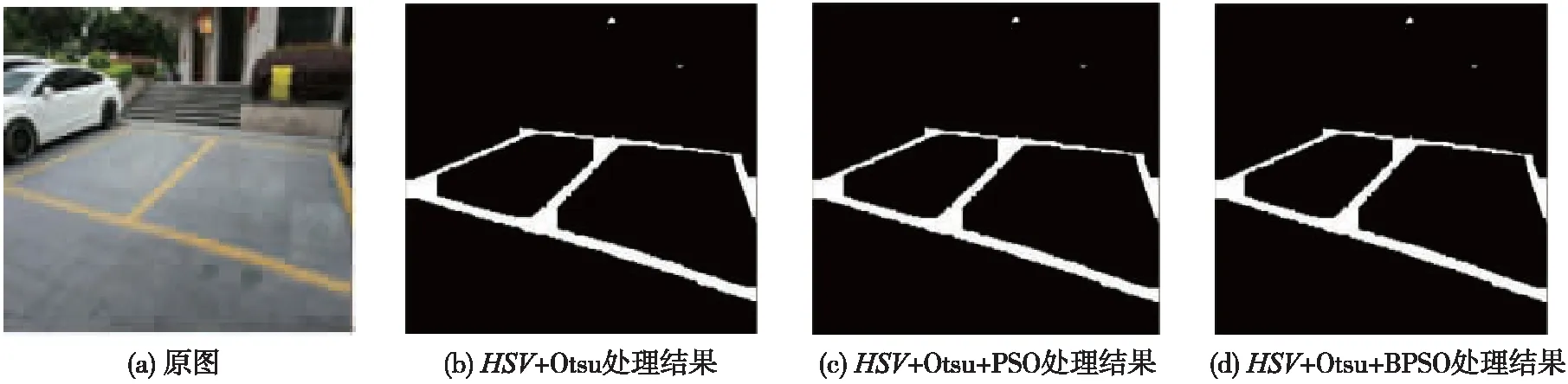
图7 相对复杂环境图像车位线分割结果

图8 相对单一环境图像车位线分割结果

图9 相对单一、复杂图像车位线分割结果
从表1和表2中可以看出,在对HSV空间H、S分量依次过滤非目标信息时,利用单一的Otsu算法进行分割运行时间都较长,迭代次数都是256次,虽然求得最优阈值所占比例最高。但计算量大、运行时间长,难以满足车位线提取的实时性;Otsu+PSO算法相对于Otsu算法有所改进,算法的迭代次数大幅度降低,运行时间也减少,虽然求得最优解所占的比例没有Otsu算法高,但整体性能明显优于Otsu算法;Otsu+BPSO算法在Otsu+PSO算法的基础上对PSO算法进行改进,省去了惯性权重w、速度v和加速度常数等参数,其简单无参数和结果数据也显示其运行时间进一步缩短,迭代次数也进一步的减少,求得最优解所占比例也相对较高。基于HSV空间分量的3种方法的分割效果基本相差不大,Otsu+BPSO整体性能优于其他2种算法。
6 结语
分别对比相对单一的车位线图像与相对较复杂的车位线图像分割结果可以看出,传统的RGB直接处理方式,由于之间相关性较强且分割时易受光照不均匀、背景的影响,分割结果不理想。笔者引入了HSV空间,利用H、S分量依次过滤非车线信息,并利用形态学以及Hough变换法的处理方式有效地将车位线提取出来,分割结果较好。传统的Otsu算法迭代次数太多、运行时间长,难以满足实时性需求。在传统的Otsu算法的基础上引入了粒子群优化算法以及骨干粒子群优化算法,对传统的Otsu算法进行优化求最优阈值,并进行3组对比,结果表明,提出的改进的Otsu+BPSO算法在相对单一以及相对复杂环境的车位线分割效率明显优于传统的Otsu算法,具有较强的实用性。
