基于导波传播模型的MUSIC损伤识别算法

左浩，许才彬，杨志勃

1. 长安大学 工程机械学院，西安 710064

2. 重庆大学 航空航天学院，重庆 400044

3. 西安交通大学 机械工程学院，西安 710049

复合材料结构的比强度和比模量高，并具有可设计性、耐高温、耐疲劳、热稳定性好等优点，优良的力学性能使其被广泛应用于航空航天、能源电力、国防工业、交通运输等领域[1]。中国自主研发的C919大型客机的复合材料重量占比达12%以上，复合材料主要用于平尾、垂尾、后机身以及后压力球面框等结构[2]。“一代材料，一代飞机”，复合材料已经成为衡量新一代民用客机先进性的重要标志[3]。复合材料在减轻结构重量、提高承载能力及稳定性等方面性能卓越，但是复合材料结构破坏机理和损伤演化过程十分复杂，表现形式多样，损伤判别困难。复合材料结构损伤主要有纤维断裂、基体开裂、层间分层和纤维脱粘等，这些微小损伤不易发现，潜在危险很大，这些不可目视的结构损伤会导致结构强度降低可达65%[4]，严重威胁航班飞行安全。

超声导波是应力波的一种，和传统的无损检测技术相比，超声导波具有能量衰减小、对包括结构表面和内部的多种损伤敏感、一次激励可检测整个传播路径上的损伤情况等优良特性，被认为是最具前景的结构损伤检测方法之一[5-7]。基于超声导波的结构健康监测主要是检测和定位重点监测区域的损伤[8-9]。目前广泛采用的基于导波的结构损伤识别算法利用损伤信号与基准信号的差信号表征损伤散射信号，并以此检测结构损伤状态。然而，由于超声导波的多模态和频散特性使得传感器网络采集的原始信号波包与结构损伤和边界反射回波重叠严重，从而导致导波时域分辨率下降，难以提取损伤特征信息，目前对于实际工程结构损伤检测和定位的挑战仍然存在[10]。

阵列信号处理技术是现代信号处理的一个重要分支，随着信号处理技术应用领域的不断扩大，基于空间谱估计的阵列信号处理技术已被广泛应用于雷达、通讯、声呐、地震和生物医学等诸多领域[11]。Schmidt[12]提出的多重信号分类算法(Multiple Signal Classification，MUSIC)是一种基于信号子空间的高分辨率阵列信号处理方法，该算法通过将传感器阵列采集得到信号的协方差矩阵进行特征值分解，从而将信号观测空间划分为噪声子空间和信号子空间，利用信号子空间和噪声子空间的正交性估计信号参数。随后，美国德克萨斯农工大学Han和Kim[13]提出了适用于板类结构健康监测的时间反转-多重信号分类波束形成算法，有效地识别结构损伤类型、位置及相对大小。中国温州大学钟永腾等[14,15]将多重信号分类算法引入复合材料结构健康监测领域，提出了基于梅花阵列的冲击定位算法实现了复合材料冲击定位。该方法基于近场波源假设，即传感器阵列采集到的波阵面为球面波，有效地解决了结构健康监测领域中近场信号源的定位问题[16]。山东大学姜明顺等[17]通过盖氏圆定理估计低速冲击损伤数目，利用近场波源的多重信号分类算法实现了复合材料层合板结构低速冲击多损伤定位。

本文将导波传播模型与阵列信号处理技术相结合，构造了基于近场波源阵列信号的二维MUSIC损伤识别模型，利用近场阵元的导向矢量和噪声子空间的正交特性构造复合材料结构损伤定位二维MUSIC空间谱，解决了复合材料结构健康监测领域中经典MUSIC阵列信号处理技术不适用于结构损伤近场定位问题，实现了复合材料结构高精度损伤定位。

1 经典MUSIC算法

MUSIC算法的主要思想是利用传感器阵列采集得到信号的协方差矩阵进行特征值分解，得到2个互相正交的噪声子空间和信号子空间，利用这2个子空间的正交性构造相应的空间谱函数，通过谱峰搜索得到信号源的参数信息。下面以远场波源的波达方向(Direction of Arrival, DOA)参数估计的MUSIC算法为例介绍子空间算法的基本理论。

根据阵列信号传播原理，第i个传感器阵元相对于参考阵元接收到的响应信号可以表示为

(1)

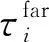
(2)

式中：θ为波源的角度。

(3)

则由M个传感器组成的均匀线性传感器阵列采集的响应信号可以改写为矩阵形式

Xfar(t)=Afar(θ)s(t)+N(t)

(4)

式中：

N(t)=[n1(t),n2(t),…,nM(t)]T

由于传感器阵列接收的响应信号与噪声不相关且相互独立，构造均匀线性阵列接收响应信号的协方差矩阵Rfar为

Rfar=AfarRsAfarH+σ2IN

(5)

式中:Rs为信号的协方差矩阵；上标H表示复共轭转置运算;σ2表示噪声的能量；IN为噪声矩阵。

根据信号子空间阵列信号处理算法，均匀线性阵列接收响应信号的协方差矩阵Rfar可以通过特征值分解算法分解为信号子空间和噪声子空间，即

(6)

式中:U和∑分别表示协方差矩阵所对应的特征向量和特征值。

根据经典MUSIC算法模型的噪声假设，各传感器阵元信道内部噪声为零均值，方差为σ2的高斯白噪声，各传感器阵元噪声之间彼此独立，且与信号之间也彼此独立

AfarHUN=0

(7)

即远场阵元的导向矢量Afar(θ)和噪声子空间UN正交。

在实际测试系统中，传感器阵列采集的信号并不是无限长而是有限的，因此信号的协方差矩阵的最大似然估计为

(8)

式中：L为信号长度。

(9)

则构造远场MUSIC空间谱作为搜索函数

(10)

通过对远场MUSIC空间谱式(10)进行谱峰搜索，得到的极值即为远场波源的角度信息。

2 近场MUSIC损伤识别算法构造

2.1 近场二维MUSIC损伤识别算法

损伤散射信号包含有损伤的位置信息，损伤散射信号可用于结构损伤识别，本文主要利用阵列信号处理技术识别结构损伤。结构中的损伤可以认为是距离传感器阵列较近的次波源。因此，采用阵列信号处理技术的结构损伤识别算法基于近场假设，传感器阵列采集到的响应信号可以认为是球面波。

板类结构表面布置均匀线性传感器阵列近场模型如图1所示。m为参考阵元；r1,r2,…,rm，…，rM为波源P0到第i个传感器的距离；R1，R2，…，Rm,…，RM为损伤至各个传感器阵元的距离。假设在已知的位置P0(θ0,R0)激励中心频率为fc的导波，激励信号波形为s0(t)。对于无损伤板类结构，传感器阵列采集到的响应信号只有直达波信号，如图1(a)所示。结构损伤经常被认为是次波源，对于损伤板类结构，传感器阵列采集到的响应信号由直达波信号和损伤散射信号组成，其中损伤散射信号如图1(b)所示。

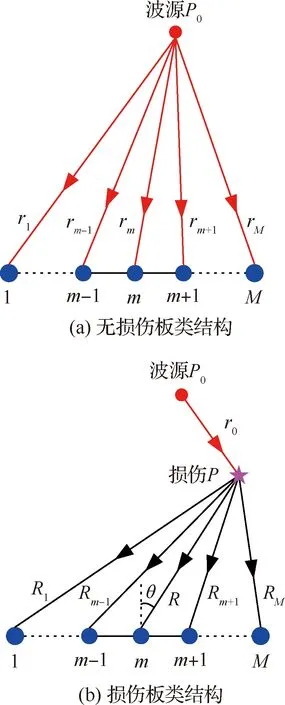
图1 均匀线性传感器阵列近场模型

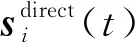
(11)

式中:S0(ω)为激励信号s0(t)的傅里叶变换;ω为角频率；c为波速;ri为激励波源P0到第i个传感器阵元的距离，即

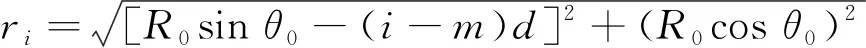
(12)

式中：d为各传感器阵元间距。

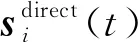
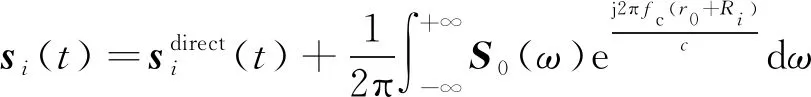
(13)

式中：

式中:r0为波源至损伤的距离;Ri为损伤至各个传感器阵元的距离。

(14)

其中损伤散射信号可以改写为

(15)

式(15)指数部分定义为近场阵元的导向矢量

(16)

(17)

由于损伤散射模式包含了散射的相位误差，相位误差会降低成像性能[19]。利用希尔伯特变换将散射信号变换为解析信号以减小相位误差对成像性能的影响。

Rnear=E[Xscattered(t)XresidualH(t)]

(18)

式中:

式中:h{·}表示希尔伯特变换。

与远场波源假设类似，近场波源假设的互相关矩阵Rnear也可以通过特征值分解算法将观测空间分解至2个相互正交的子空间，即信号子空间Us和噪声子空间UN。利用近场阵元的导向矢量A(θ,R)和噪声子空间UN相互正交的特性，构造基于导波传播模型的二维MUSIC空间谱作为结构损伤位置搜索函数

(19)

式中:

A(θ,R)=

通过改变角度θ和距离R这2个参数进行近场损伤的位置搜索，即对近场二维MUSIC空间谱进行谱峰搜索，极值即为结构损伤的位置信息。

2.2 算法流程

基于导波传播模型的近场二维MUSIC空间谱算法流程如图2所示，其结构损伤定位的主要步骤为

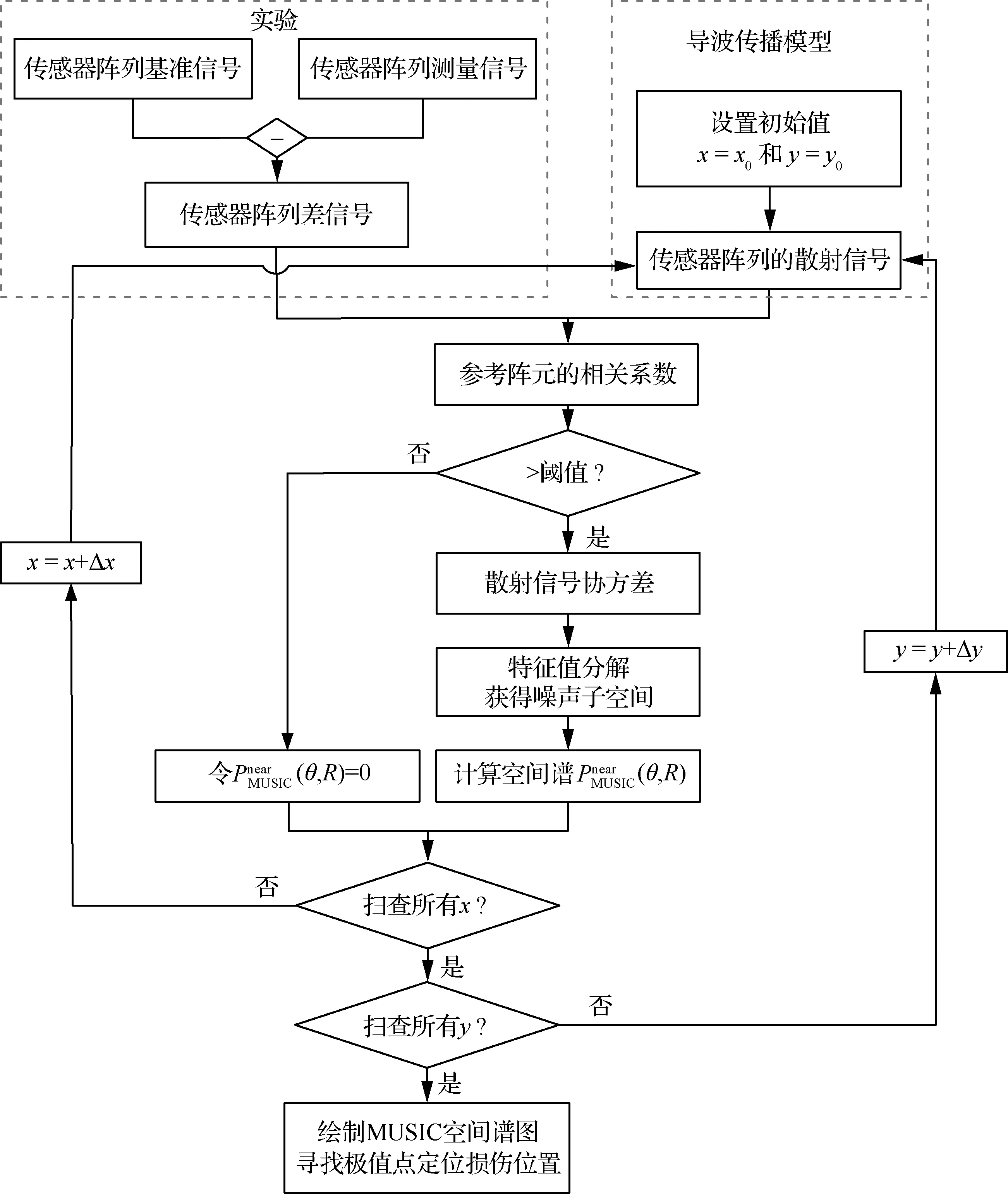
图2 基于导波传播模型的MUSIC空间谱算法流程图

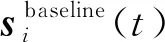
步骤2设置结构损伤初始位置参数x=x0，y=y0。

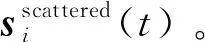
步骤4计算参考传感器阵元的差信号和损伤散射信号的相关系数，由于结构损伤具有稀疏性，大部分检测区域是无损伤，因此低相关系数所对应的位置可以认为是无损伤区域，通过设置阈值防止损伤误报。

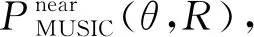
步骤6扫查下一个监测位置，重复步骤3～步骤5。

步骤7绘制二维MUSIC空间谱图，寻找极值点实现结构损伤定位。

3 算法验证

3.1 复合材料板结构损伤识别

3.1.1 数值仿真算例

本节通过数值算例将本文提出的损伤识别算法应用于复合材料板结构损伤识别。复合材料板结构的尺寸参数为1 000 mm×1 000 mm×2 mm，在距离激励信号源250 mm位置对称布置7个测点作为传感器阵列接收导波信号，且各传感器阵元之间的间距为10 mm，如图3(a)所示。该结构为石墨环氧树脂复合材料板结构，材料铺层角度为[+45°/-45°/0°/90°]S，材料参数为弹性模量E1=144.48 GPa，E2=E3=9.63 GPa，剪切模量G23=G13=G12=4.128 GPa,泊松比μ23=0.3，μ12=μ13=0.02，密度ρ=1 389 kg/m3,且边界条件为四边自由。在复合材料板结构的中心位置施加中心频率fc=50 kHz汉宁窗调制五周期正弦信号模拟导波激励信号，其时域波形和频域波形如图3(b)所示。

复合材料板结构通过减小刚度的方法模拟穿透裂纹，数值模拟损伤D1与传感器阵元4的相对位置为(-200 mm,150 mm)，如图3(a)所示。

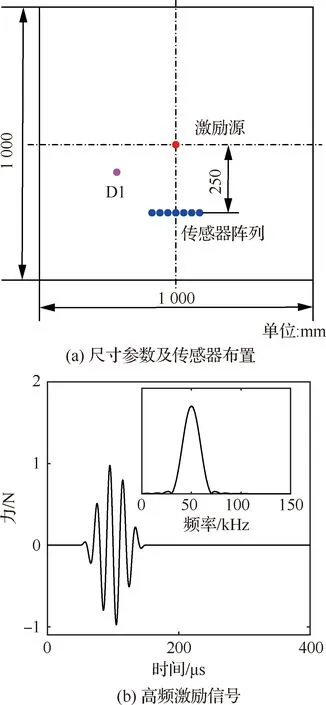
图3 复合材料板结构和高频激励信号

该数值仿真算例利用文献[20]提出的基于CPU/GPU异构并行的小波有限元法模拟复合材料板结构导波传播全波场响应：首先，通过数值仿真健康复合材料板结构的导波传播过程，采集得到基准信号；然后，将结构损伤添加至复合材料板结构中，采集得到测量信号；最后，通过测量信号减掉基准信号得到的差信号就是由于结构损伤存在引起的损伤散射信号。图4所示为传感器阵元4采集健康信号和损伤信号。

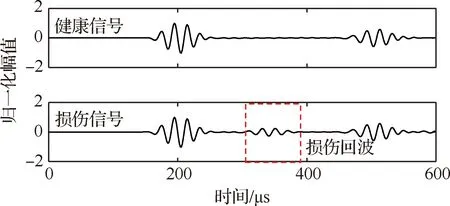
图4 传感器阵元4采集健康信号和损伤信号

为了评价本文提出损伤识别算法的性能，定义损伤实际位置与损伤识别结果的距离作为损伤识别误差参数

(20)

式中:(x*,y*)为结构损伤的实际位置;(x,y)为结构损伤的识别位置。

基于导波传播模型的二维MUSIC空间谱损伤识别算法得到的复合材料板结构损伤识别结果如图5所示(圆圈表示损伤实际位置，三角表示损伤识别结果)。从图5(a)中可以看出，利用本文提出的基于导波传播模型的二维MUSIC空间谱损伤识别算法成功地识别了复合材料板结构的D1损伤，且D1损伤识别结果与损伤实际位置基本重合，损伤识别结果(-203 mm,146 mm)与实际损伤的距离误差为5.0 mm，识别精度非常高。此外，利用经典MUSIC算法识别损伤结果的位置参数为(-164 mm,117 mm)，如图5(b)所示，损伤识别结果与实际损伤的距离误差达48.8 mm，损伤识别结果误差较大。

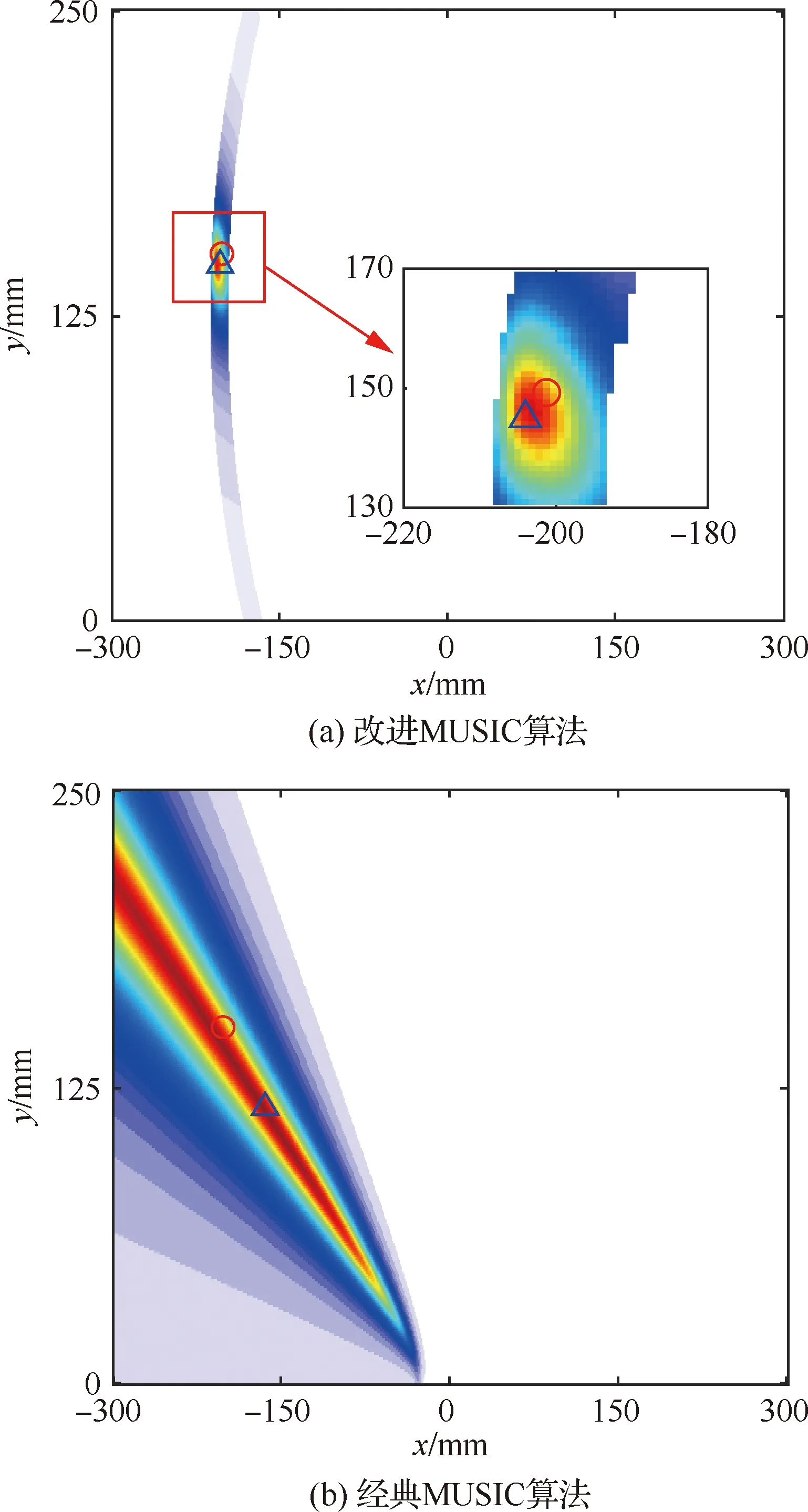
图5 复合材料板结构损伤数值仿真空间谱估计图

为了验证算法的噪声免疫能力，在数值仿真算例中，研究了不同信噪比(Signal-Noise Ratio, SNR)的高斯白噪声对结构损伤定位精度的影响，如图6所示。

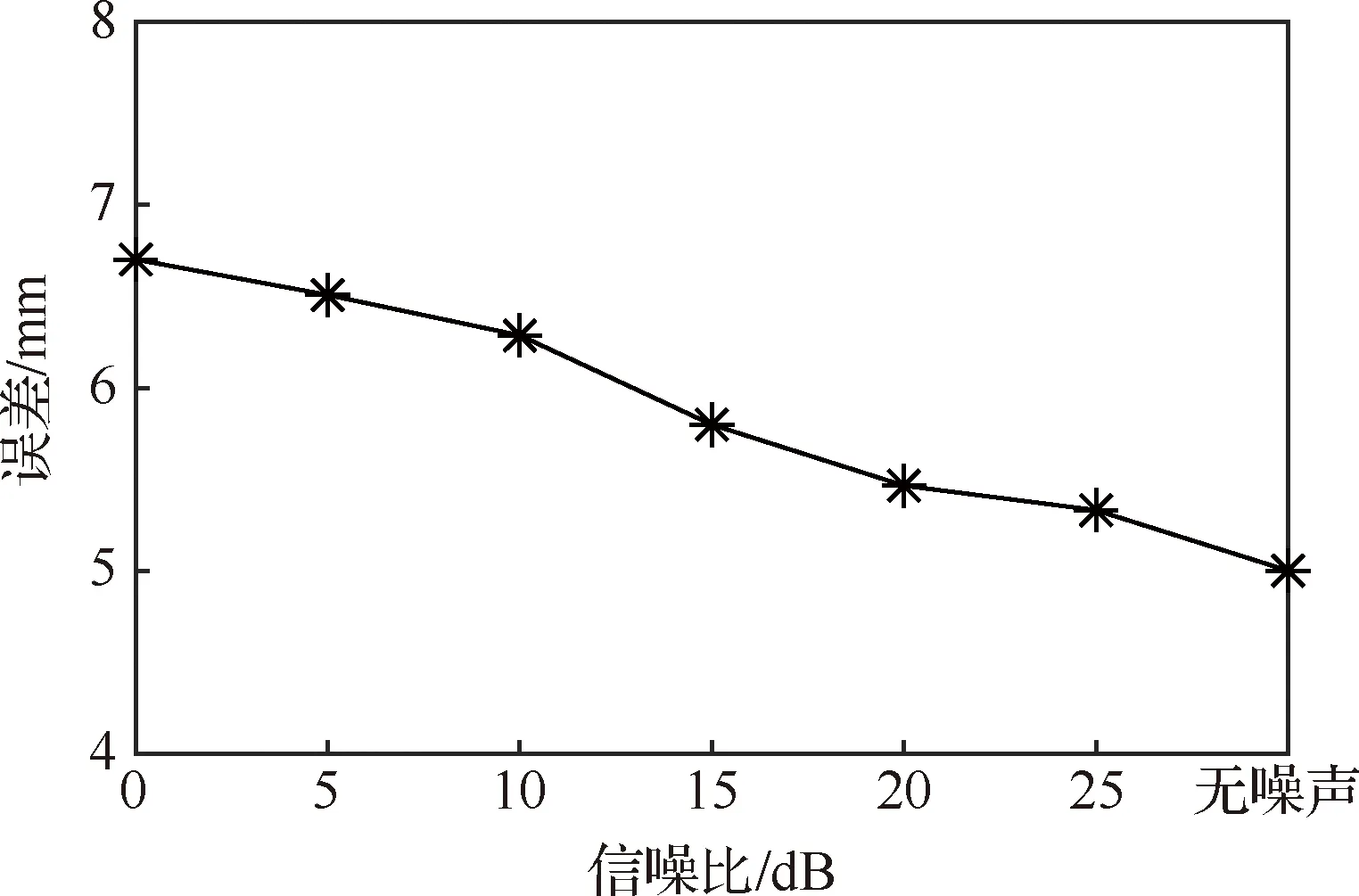
图6 信噪比与损伤识别精度的关系

从图6中可以看出，当信噪比为0 dB时，结构损伤定位误差最大为6.7 mm；随着信噪比增大，结构损伤定位误差逐渐减小，当信噪比为25 dB 时，结构损伤定位误差为5.3 mm；在无噪声情况下，结构损伤定位误差仅为5.0 mm。本文提出的基于导波传播模型的二维MUSIC空间谱损伤识别算法利用导向矢量与噪声子空间相互正交特性识别结构损伤，具有较好的鲁棒性。

3.1.2 实验验证

本节通过复合材料板结构的损伤识别实验进一步验证本文提出的基于导波传播模型的二维MUSIC空间谱损伤识别算法的有效性和精确性。

在实验过程中，通过在复合材料板结构表面粘贴附加质量块来模拟结构损伤引起局部刚度变化[21]。因此，利用2个直径为10 mm的圆柱形磁铁吸附在复合材料板结构表面模拟结构损伤，通过改变圆柱形磁铁的位置模拟不同的分层损伤位置。为了验证算法的适用性，在复合材料板结构模拟不同损伤位置参数如表1所示。

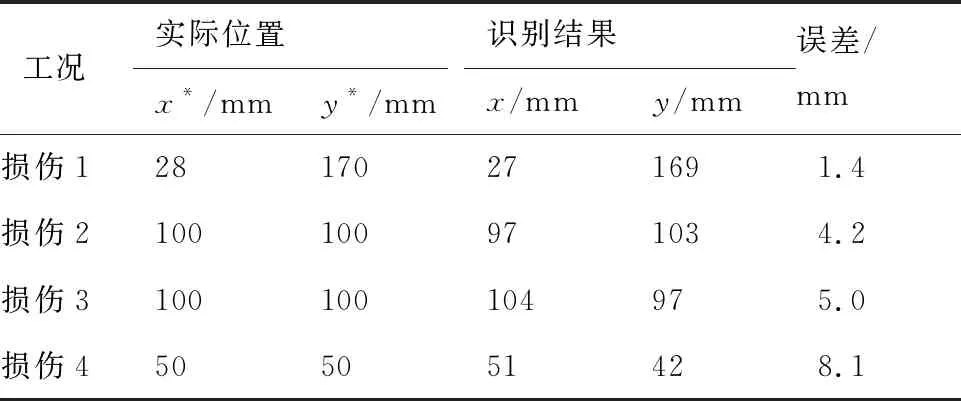
表1 复合材料板结构损伤识别结果

从表1可以看出，复合材料板结构4种不同的损伤位置参数均被成功识别出来，损伤识别精度较高。为了与损伤实际位置更好比较，图7给出了表1中复合材料板结构损伤识别结果与实际损伤位置的示意图(圆圈表示损伤实际位置，三角表示损伤识别结果)。从图7中可以看出，复合材料板结构损伤识别结果较好，损伤1的识别结果与损伤实际位置误差最小，距离误差仅为1.4 mm；损伤4的识别结果误差较大，最大的距离误差为8.1 mm。

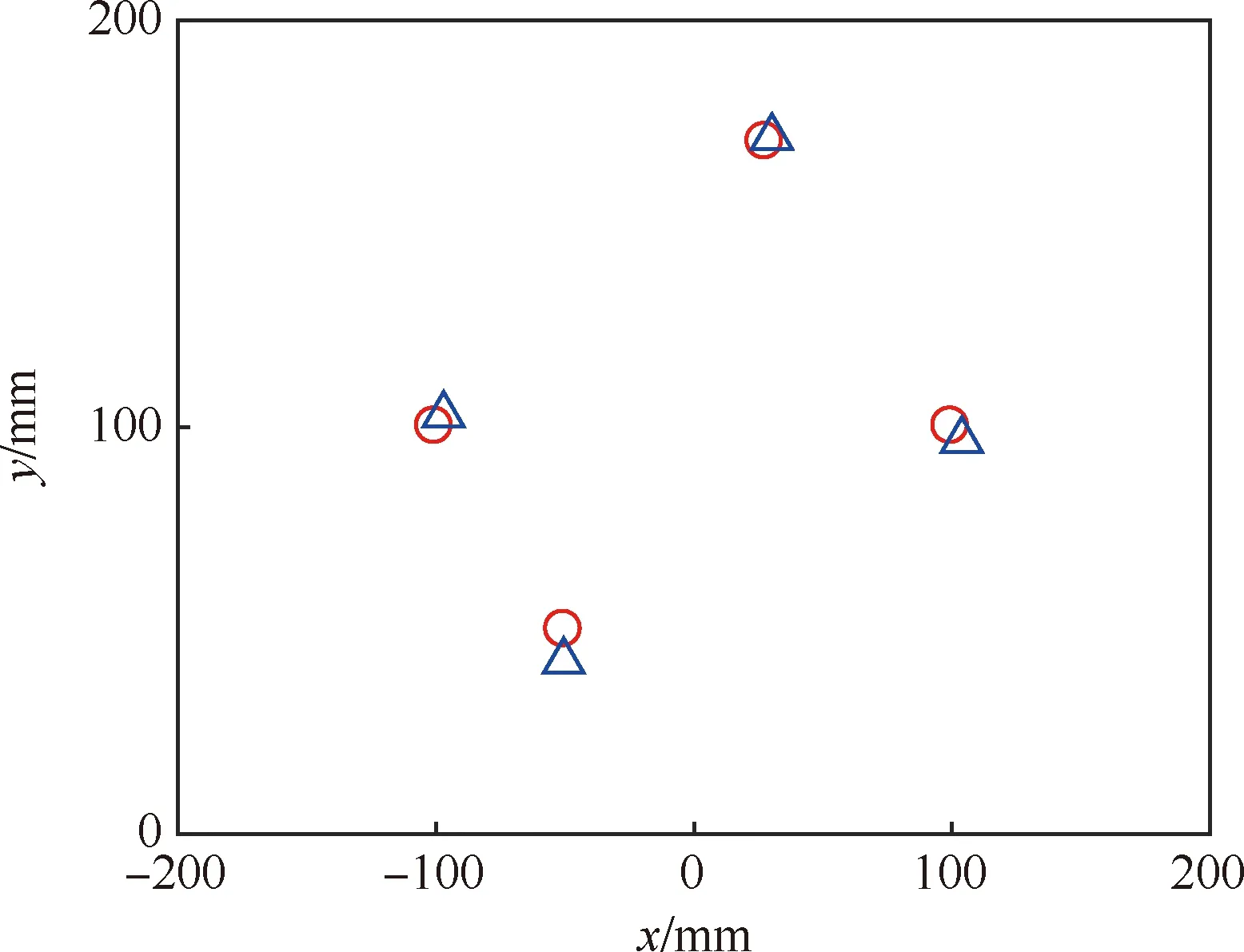
图7 复合材料板结构损伤识别结果

通过上述的数值算例与实验结果表明本文提出的基于导波传播模型的二维MUSIC空间谱损伤识别算法适用于板类结构的损伤识别，特别是复合材料板结构损伤识别的位置精度和分辨率都非常高。

3.2 飞机垂直尾翼结构损伤识别

3.2.1 飞机垂直尾翼结构

本文实验对象为某飞机垂直尾翼结构，该垂直尾翼结构由表面碳纤维增强复合材料板结构和4条工字型加强筋组成，其结构和尺寸参数如图8和图9所示。该飞机垂直尾翼结构的尺寸参数为700 mm×600 mm×4 mm。

图8 飞机垂直尾翼结构

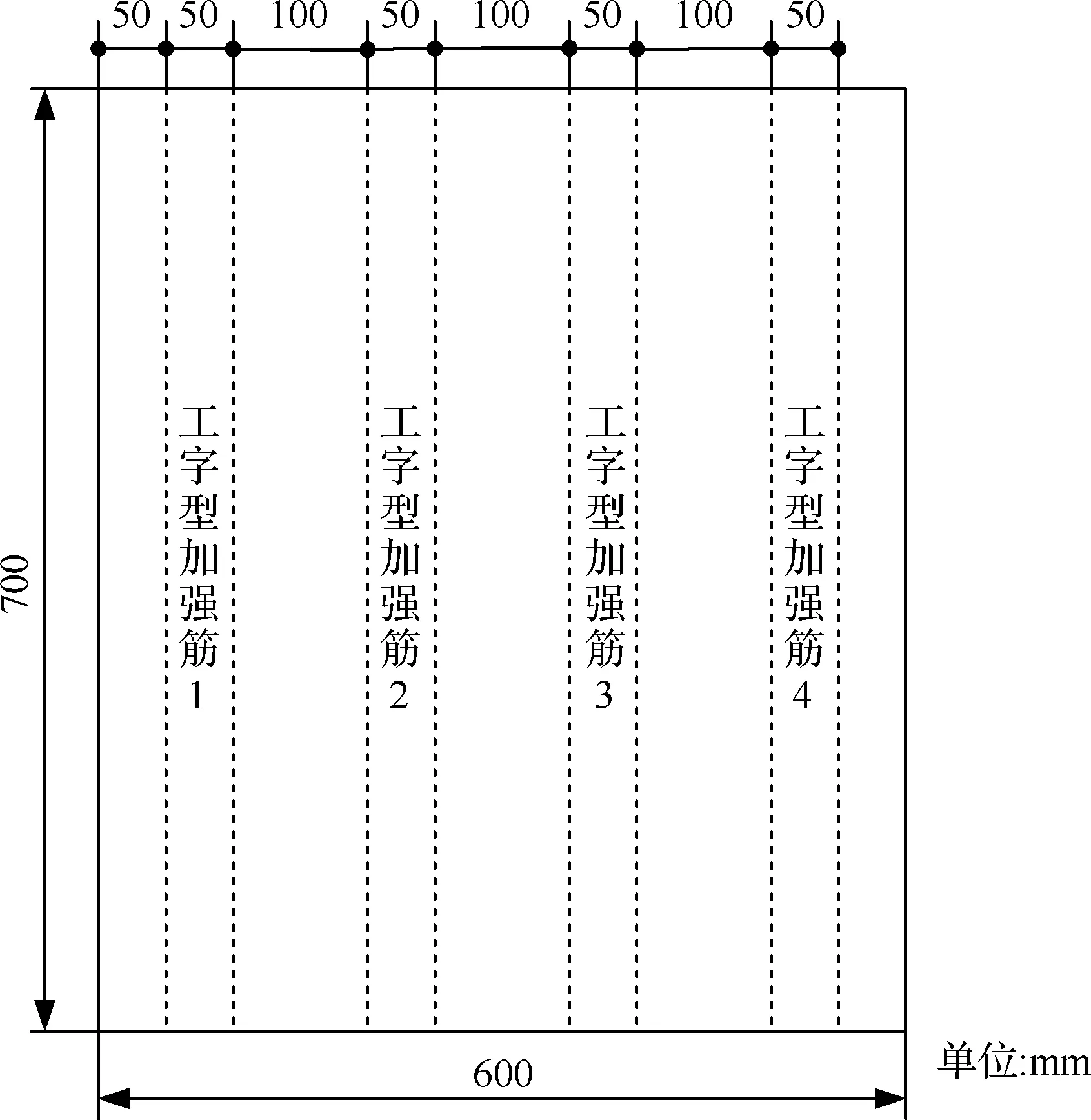
图9 飞机垂直尾翼结构尺寸示意图

3.2.2 飞机垂直尾翼结构损伤识别策略

由于飞机垂直尾翼结构的工字型加强筋对导波信号衰减和频散特性影响严重，将对损伤识别算法准确性影响非常大。因此，在飞机垂直尾翼结构损伤识别时需要制定相应的监测策略，以减小加强筋对导波传播特性的影响。该垂直尾翼结构损伤监测策略如图10所示，即将该飞机垂直尾翼结构划分为6个监测区域，利用本文提出的基于导波传播模型的二维MUSIC空间谱损伤识别算法监测2个加强筋之间的区域。在该监测区域内，导波直达波信号与损伤散射信号均会早于工字型加强筋反射回波信号到达传感器阵列，从而避免了工字型加强筋对导波传播特性的影响。

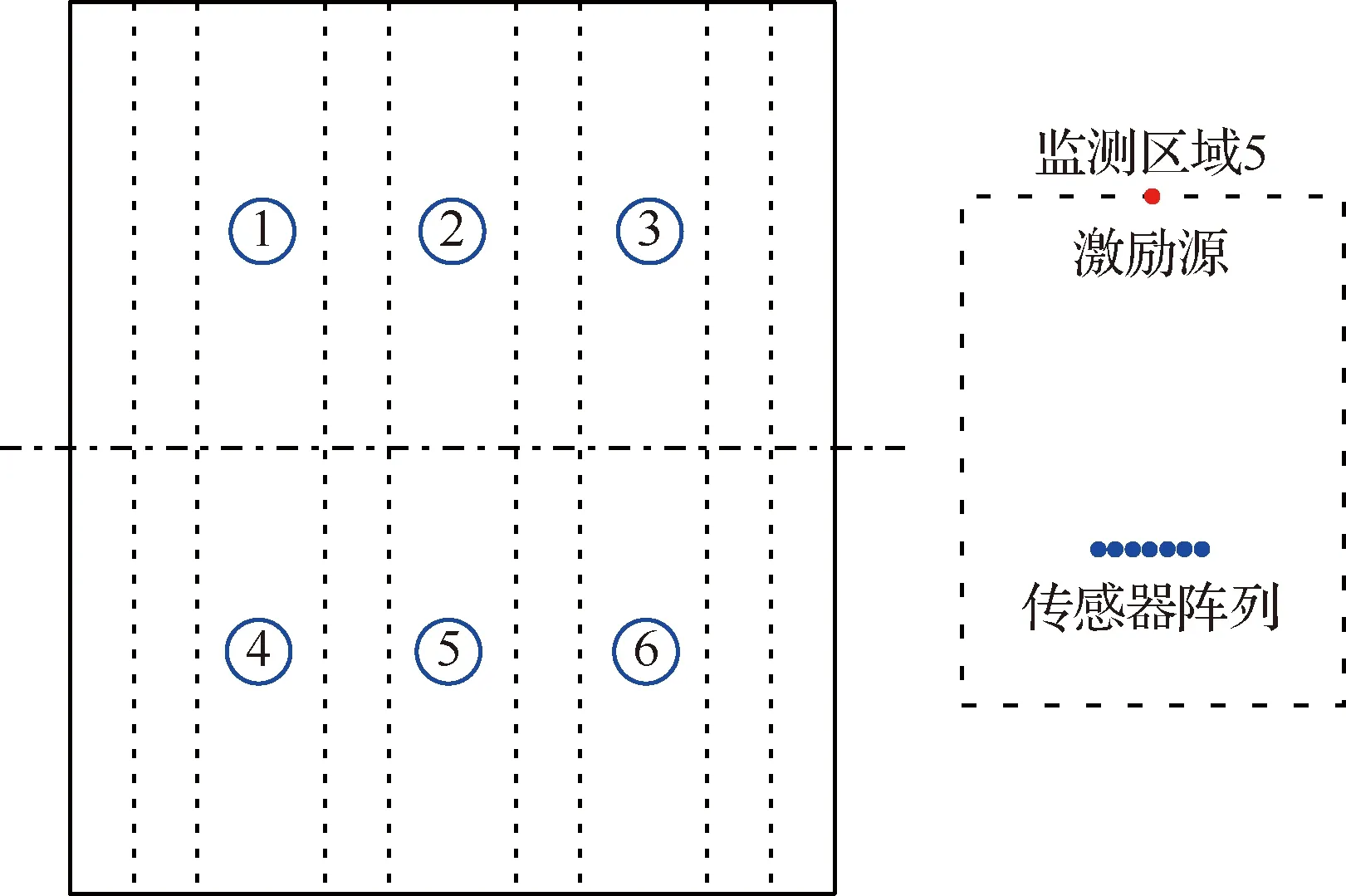
图10 飞机垂直尾翼结构损伤监测策略

飞机垂直尾翼结构表面碳纤维增强复合材料板具有各向异性，其导波传播群速度也与传播方向有关。此外，当复合材料的力学性能参数不准确时，采用理论计算的群速度与实际情况不一致，在后续结构损伤识别过程中会造成较大的定位误差。因此，本文利用实验得到的导波传播速度对该垂直尾翼结构导波传播模型进行修正，以减小理论波速与实际波速之间的误差。

本文将利用传感器阵列采集得到导波传播不同方向群速度的相关性，通过健康结构导波响应信号计算得到平均群速度代替各个方向的导波群速度，即

(21)

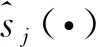
3.2.3 飞机垂直尾翼结构损伤识别实验验证

飞机垂直尾翼结构损伤识别实验系统如图11所示。该复合材料结构损伤诊断实验平台的硬件系统主要包括NI PXI-1042Q系统，PIEZO功率放大器、PZT压电片以及各种信号传输导线。其中NI PXI-1042Q系统为整个实验系统的核心硬件，它包含1个NI PXI 5412任意波形发生板卡和4个14位采样率为100 MS/s的NI PXI 5122数据采集板卡，可同时作为信号发生器和信号采集器，且可以同时采集8通道的振动响应信号。该实验系统可以实现任意激励信号的发生、功率放大以及传感信号的采集。

图11 飞机垂直尾翼结构损伤识别系统

飞机垂直尾翼结构监测区域5中传感器及损伤位置如图12所示。在监测区域5布置PZT0-PZT7压电陶瓷传感器阵列，其中PZT0作为激励源，PZT1-PZT7组成线性传感器阵列，各传感器阵元的间距为10 mm，其中飞机垂直尾翼结构监测区域5中各传感器位置坐标参数如表2所示。激励信号选择汉宁窗调制的五周期正弦信号，中心频率为fc=30 kHz，数据采样频率为fs=10 MHz。

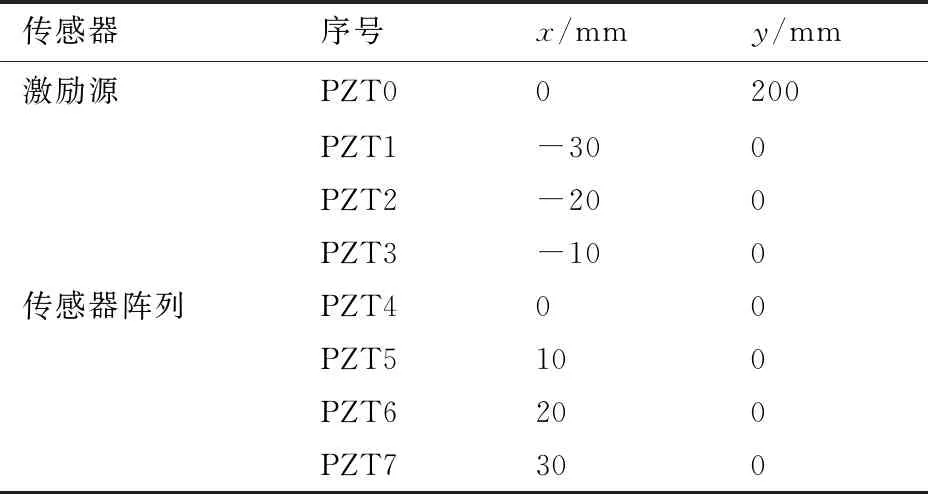
表2 飞机垂直尾翼结构传感器位置坐标

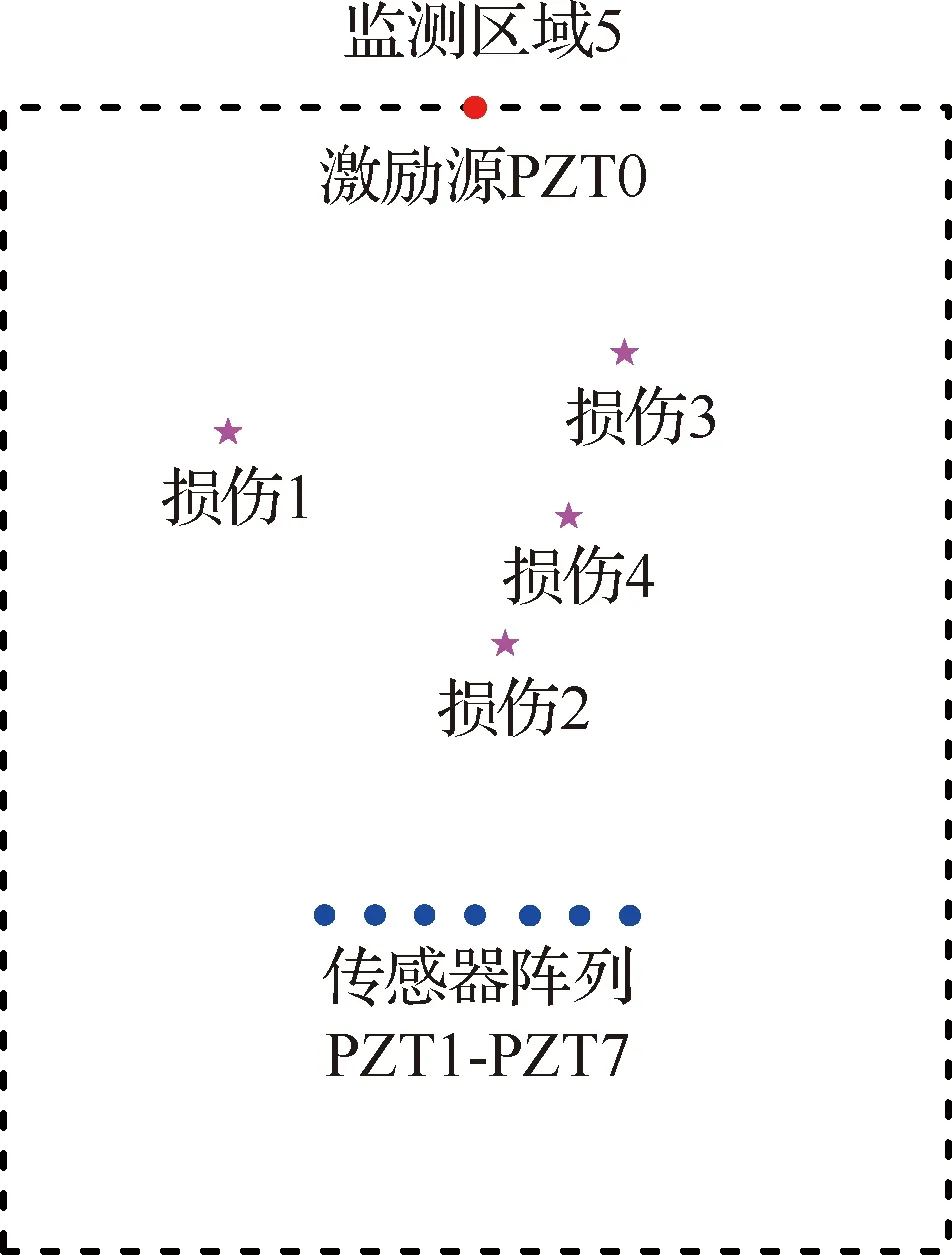
图12 飞机垂直尾翼结构传感器及损伤位置

在实验过程中，通过在飞机垂直尾翼结构表面粘贴附加质量块来模拟结构损伤引起局部刚度变化，不同损伤位置参数如表3所示。

表3 飞机垂直尾翼结构损伤位置参数

利用本文所提出的基于导波传播模型的二维MUSIC空间谱损伤识别算法对该飞机垂直尾翼结构损伤1进行识别，损伤识别结果如图13所示(圆圈表示损伤实际位置，三角表示损伤识别结果)。从图13中可以看出，飞机垂直尾翼结构损伤1被成功识别出来，损伤1的识别位置参数为(-38 mm,110 mm)，定位误差为2.0 mm，具有很高的损伤定位精度和分辨率。

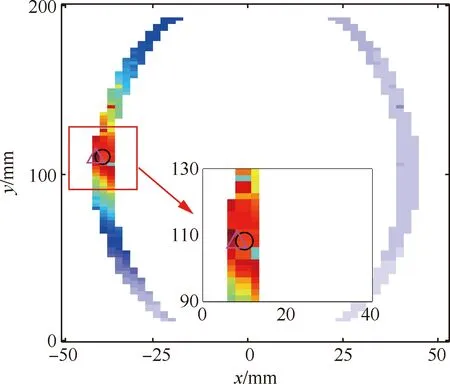
图13 飞机垂直尾翼结构损伤空间谱估计图

飞机垂直尾翼结构不同位置损伤识别结果如表4所示，4个损伤的位置参数均被成功地识别。该飞机垂直尾翼结构损伤1的损伤识别结果与实际损伤位置定位误差最小，两者的位置误差为2.0 mm， 损伤定位精度最高；损伤4的损伤识别结果为(24 mm,68 mm)，其损伤识别结果与实际损伤位置(20 mm,80 mm)定位误差最大，两者的位置误差为12.6 mm。为了与损伤实际位置参数更好地比较，图14给出了表4中飞机垂直尾翼结构损伤识别结果与实际损伤位置的比较示意图(圆圈表示损伤实际位置，三角表示损伤识别结果)，损伤识别效果较好。飞机垂直尾翼结构损伤识别的实验结果表明：本文提出的基于导波传播模型的二维MUSIC空间谱损伤识别方法对复杂复合材料结构如飞机垂直尾翼结构损伤定位具有较高的定位精度和分辨率，损伤识别位置误差最大为12.6 mm，损伤识别效果较好，实现了复杂复合材料结构的损伤识别。

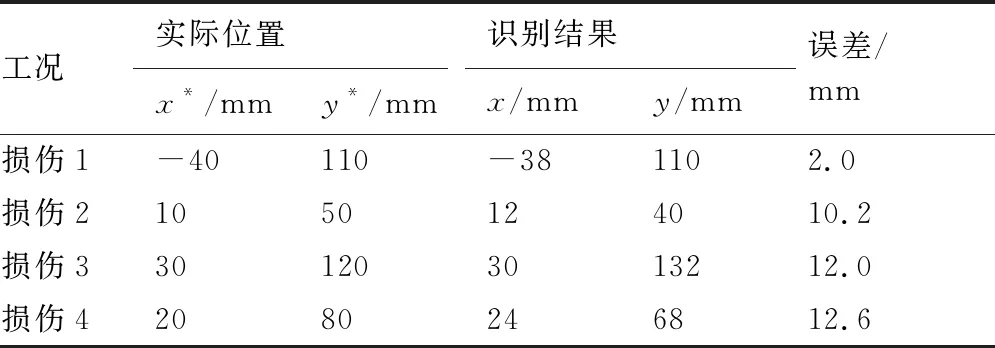
表4 飞机垂直尾翼结构损伤识别结果

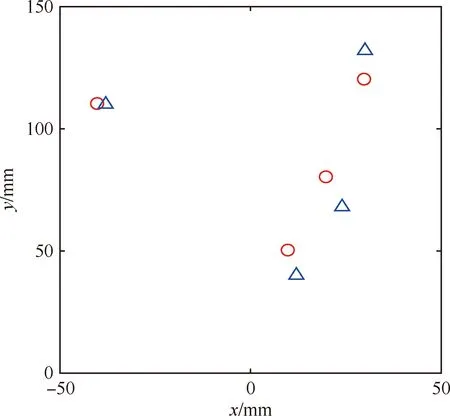
图14 飞机垂直尾翼结构损伤识别结果

4 结 论

本文提出了基于导波传播模型的二维MUSIC空间谱损伤识别算法，通过将超声导波传播模型引入损伤识别模型，构造了导波传播模型的损伤散射信号和实验差信号的互相关矩阵，利用近场阵元的导向矢量和噪声子空间相互正交的特性构造二维近场MUSIC空间谱。利用数值仿真算例验证了算法的有效性，并在复合材料板结构和飞机垂直尾翼结构进行了实验验证，数值仿真与实验结果表明该损伤识别算法能够有效地识别复合材料板结构的损伤位置信息，具有很高的定位精度和分辨率。该方法可为后期开展大型复合材料结构损伤检测与结构健康监测提供参考方法与解决途径。