飞行控制律对体自由度颤振特性影响试验

雷鹏轩，余立，陈德华，吕彬彬,*

1. 中国空气动力研究与发展中心 空天技术研究所，绵阳 621000

2. 中国空气动力研究与发展中心 高速空气动力研究所，绵阳 621000

飞翼布局飞行器在气动升阻比、隐身性能、结构效率等3个方面具有先天的优势，已成为下一代军事飞行器平台的首选布局形式。为了充分发挥结构重量优势，新一代飞翼飞行器多采用轻质复合材料，使其具有明显的结构柔性，特别是一些大展弦比飞翼飞行器，其结构弹性振动一阶固有频率仅1 Hz或更小，另一方面飞翼飞机为无尾布局，俯仰转动惯量小，纵向短周期运动模态频率高，因此极易发生弹性振动模态与刚体短周期模态耦合，在远低于设计限制的飞行速度下发生一种动力学失稳现象，造成结构破坏与飞行器坠毁[1-2]。这种由于刚体运动参与而造成的气动弹性失稳现象被称为体自由度颤振(Body Freedom Flutter, BFF)。

2003年美国空军研究实验室(Air Force Research Laboratory, AFRL)发起了SensorCraft项目[3]。项目中洛·马公司提出了一款飞翼布局无人机SC005，经研究发现体自由度颤振成为限制该飞机包线的主要制约[4]。2007年洛·马公司在NASA兰利研究中心TDT风洞中开展了样机SC006的体自由度颤振风洞试验，详细地研究了体自由度颤振现象，检验了颤振抑制控制律的有效性[5]。2010年AFRL联合洛·马公司提出了建立X-56A飞行演示平台计划(Multi-Utility Technology Testbed, MUTT)[6-8]，其目的之一就是采用飞行试验研究体自由度颤振，发展气动弹性力学/飞行力学综合控制技术(Integrated Flight and Aeroelastic Control, IFAC)，目前该项目仍在继续。2015年美国明尼苏达大学开展了飞翼飞机(mAEWing1, mAEWing2)的体自由度颤振研究[9-10]，分析了该无人机在开环与闭环控制下的稳定性[11-12]，并于2017年6月完成了体自由度颤振及其抑制飞行演示验证试验[13]。目前国外关于体自由度颤振及其抑制技术的研究逐渐成为一个热点。

在国内，2017年西北工业大学谷迎松等开展了弹性绳支撑下的平板外形全模飞翼体自由度颤振风洞试验[14]。北京航空航天大学黄超等开展了半模模型的体自由度颤振及其主动抑制风洞试验研究[15-16]。相比于国外，目前国内关于体自由度颤振的研究刚刚起步，研究对象多以开环模型为主，并不考虑飞行控制律的影响。

飞行控制系统是真实飞机必不可少的一部分，对于传统的弯扭耦合颤振问题可以忽略，但对于体自由度颤振问题，颤振发生时飞机刚体俯仰姿态将剧烈变化，随之而来的姿态保持控制必不可少。有研究表明飞行控制律会显著影响体自由度颤振特性[4]，国内已开展过计算研究[17]，但还未开展试验与计算的综合研究。鉴于此，本文开展了飞行控制律对飞翼飞机体自由度颤振特性的影响研究，针对自主设计的颤振试验模型开发了相应的俯仰姿态保持控制律，通过风洞试验与频域计算获得了不同刚体自由边界条件下的开环/闭环体自由度颤振特性，研究了闭环增益对体自由度颤振特性的影响规律，并简要分析了影响机理。

1 试验与计算方法

1.1 模 型

模型外形为中等展弦比飞翼外形，参考了目前体自由度颤振问题研究的主流平面外形(图1)。该平面外形分为机身段、翼身融合段与外翼段3段，半模展长为1.527 m，占试验段84%。外翼段共有3片舵面，单片舵面宽0.07 m，长0.37 m。

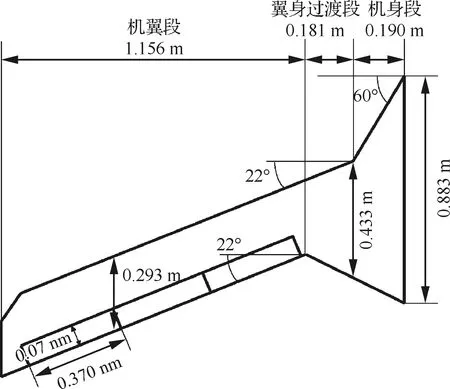
图1 模型平面外形

模型结构为自主设计，采用了与真实飞机相同的梁架蒙皮式结构布局[18]，如图2所示。模型分为机翼与机身两大部分：机身蒙皮采用碳纤维布铺层，机翼蒙皮采用玻璃纤维布铺层，机翼梁与翼肋采用航空层板制作，舵面及小翼采用碳纤维布包裹，泡沫填充。

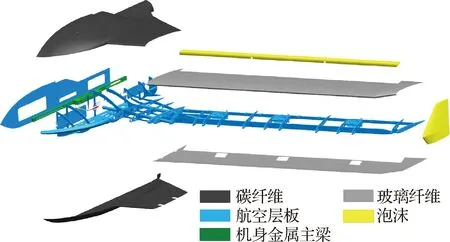
图2 模型内部结构与材料

针对实物模型建立了相应的有限元模型，如图3所示。首先对有限元模型的质量进行了修正。装配前对模型的各部件进行称重测量，以此在有限元模型中做相应修正，如表1所示。装配好的模型重4.49 kg。俯仰转动惯量并未实际测量，而是在质量修正的基础上通过有限元模型核算，约为0.356 kg·m2。

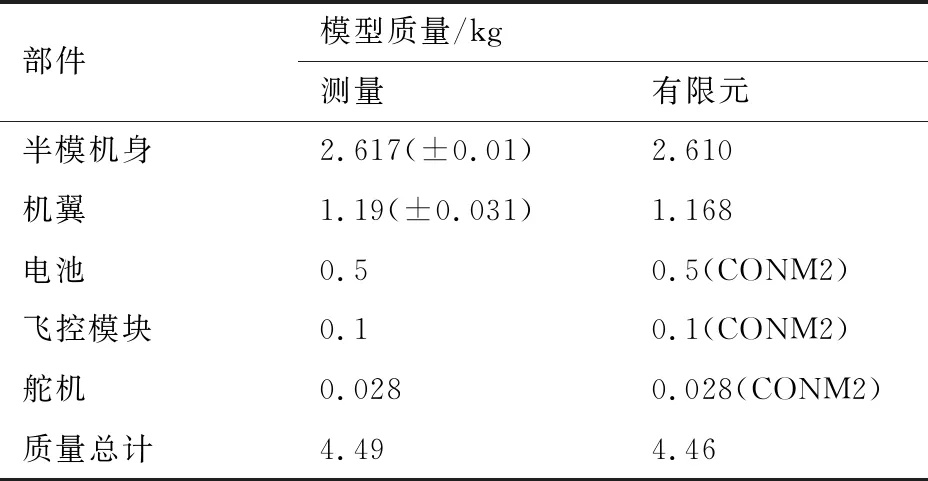
表1 实测模型部件与修正后的有限元模型质量

图3 有限元模型

其次，对有限元模型的动力学特性进行了修正。在风洞安装状态下开展了地面振动试验，使用PolyMax方法[19]进行模态参数识别。基于试验结果，对有限元模型进行了修正，表2给出了前三阶弹性模态频率的对比，可见修正后的有限元模型能较准确地反映出模型实物的动力学特性。

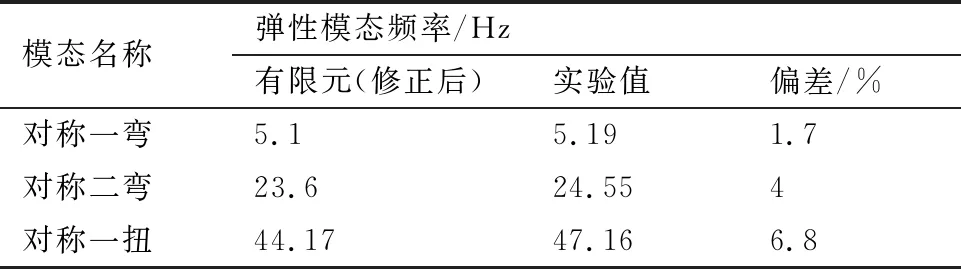
表2 地面模态试验结果

1.2 风洞与试验设备

风洞为中国空气动力研究与发展中心的1.8 m×1.4 m低速风洞，闭口试验段长5.8 m，空风洞最高风速105 m/s，闭口试验段湍流度小于0.08%。模型侧壁水平安装(图4)，模型可绕侧壁上的支撑转轴做俯仰自由转动。

图4 模型安装状态

模型与支撑转轴采用螺钉连接。通过四颗螺钉将模型机身主梁压紧在支撑转轴上(图5)，主梁上开有两条“1”型槽，用来调节支撑转轴与模型的装配位置。俯仰支撑转轴采用双轴承支撑。在洞壁外侧安装有俯仰转轴定位卡钳(图6)，采用气缸推动，体自由度颤振出现时上顶卡钳，锁死俯仰自由度，模型会退出颤振，确保试验过程中风洞和模型安全。

图5 主梁与转轴连接形式

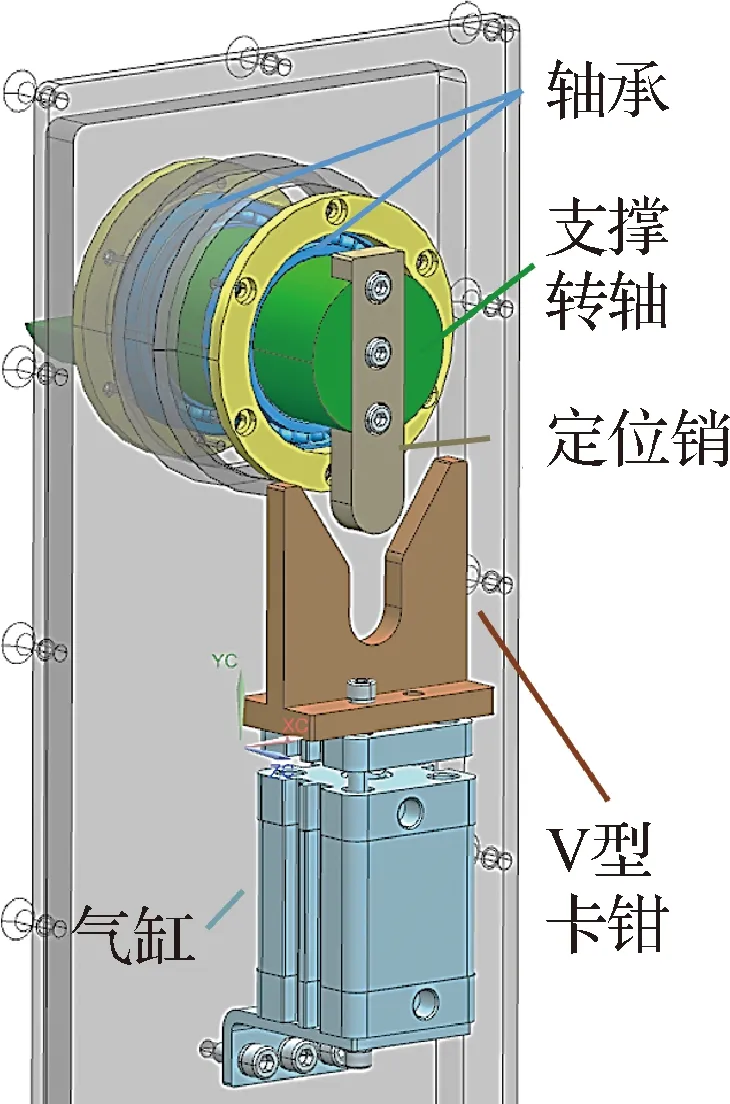
图6 俯仰支撑转轴与“V”型卡钳

采用应变片和加速度传感器测量模型的动态响应，采样率200 Hz。加速度传感器和应变片分别安装在外翼的翼梢和翼根。模型机身前部安装有空速管，用于测量风洞风速。模型内部配备有一套飞行控制系统用于模型俯仰姿态保持控制及采集记录模型俯仰角，采样率为25 Hz。飞控系统安装于机身内部半模对称面靠近质心位置处。其中俯仰角及角速度由内置于飞控系统的惯性测量单元测量，型号为ADIS16488。

1.3 俯仰姿态保持控制律

俯仰姿态保持控制采用俯仰角和俯仰角速度为反馈，根据不同的来流风速和目标俯仰角，通过调整外翼舵面，使模型保持预定的俯仰姿态。具体的控制律框图如图7所示。图中αD表示目标俯仰角，α和q分别表示实测俯仰角和实测俯仰角速度。Airspeedscaler表示空速缩放系数，KC、KP、KI、KD为4个控制器参数，δ为输出的目标舵偏角。俯仰姿态控制时，外翼的3片舵面共同偏转，各舵面偏转角度权重相同。

1.4 计算模型

颤振频域计算中非定常气动力采用偶极子网格法(Doublet Lattice Method, DLM)计算，气动面网格划分如图8所示。采用P-K法求解，马赫数Ma=0.1，空气密度1.145 kg/m3。飞行控制律采用传递函数模型建模。为简化计算模型，建模时采用俯仰角测值的一阶微分代替俯仰角速度测值，即q(s)=sα(s)。令目标俯仰角为0°，则e(s)=-α(s)。将俯仰姿态保持控制律转化为典型的单输入单输出PID控制器(图9)。结合图7的控制律框图，各环节的传递函数模型为

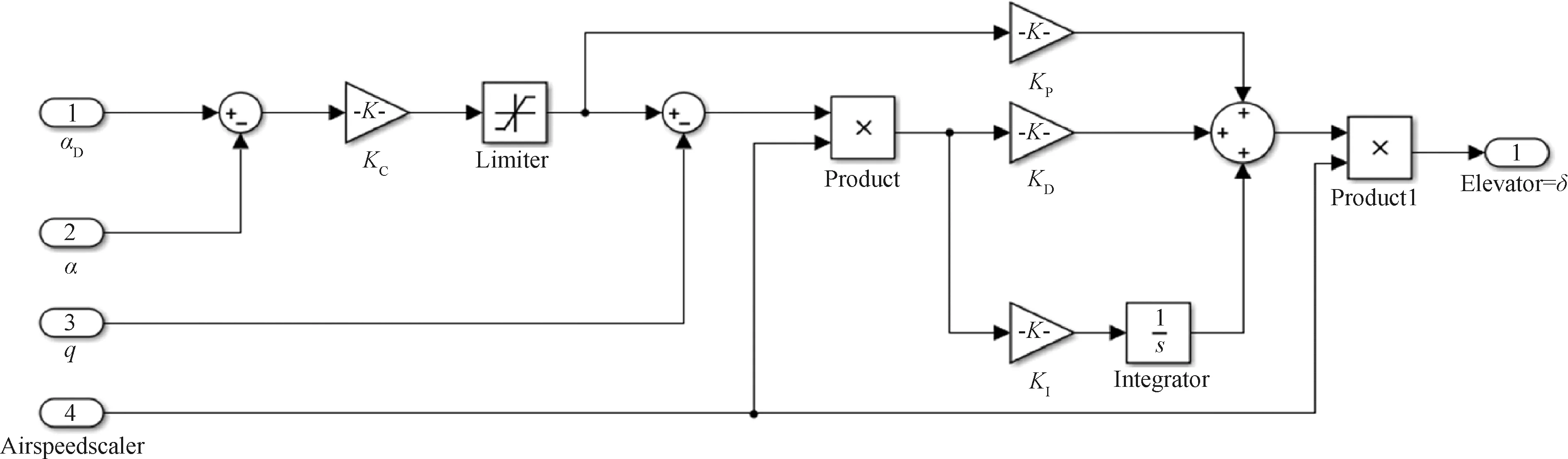
图7 俯仰姿态保持控制律框图

图8 气动面网格

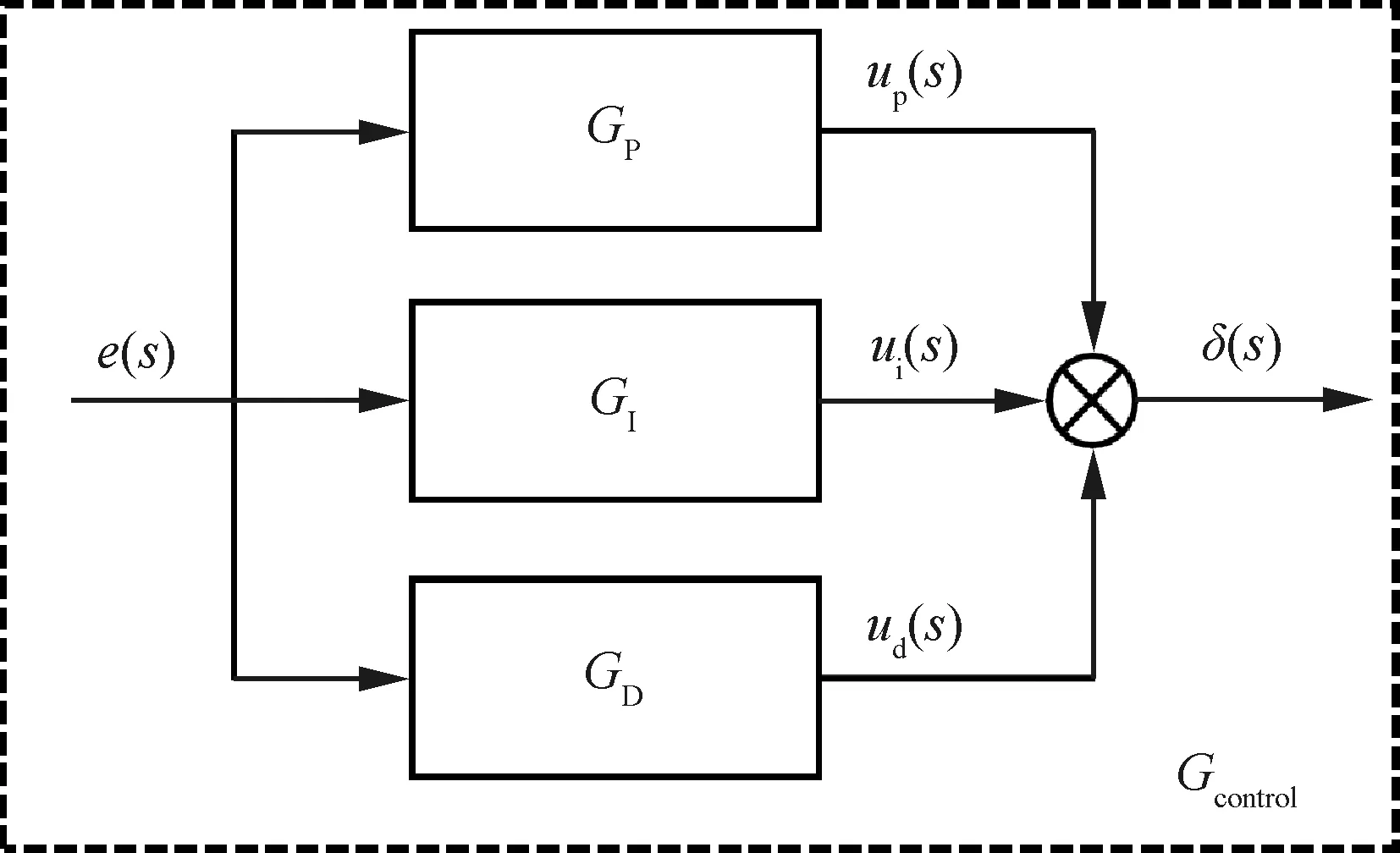
图9 计算模型中使用的俯仰姿态保持PID控制器

Gcontrol(s)=GP(s)+GI(s)+GD(s)

(1)

GP(s)=KC·KP·KAirspeedscaler

(2)

(3)

(4)

此外，在气动伺服弹性模型中还考虑了舵机模型和飞控系统的数据处理时间以及拉杆等机械结构响应滞后造成的时间迟滞影响。舵机的传递函数模型如式(5)所示。系统时滞为100 ms，采用二阶Pade近似，如式(6)所示。最终气动伺服弹性模型的方框图如图10所示，包含了飞行控制律、舵机模型、系统时滞和开环气动弹性系统。

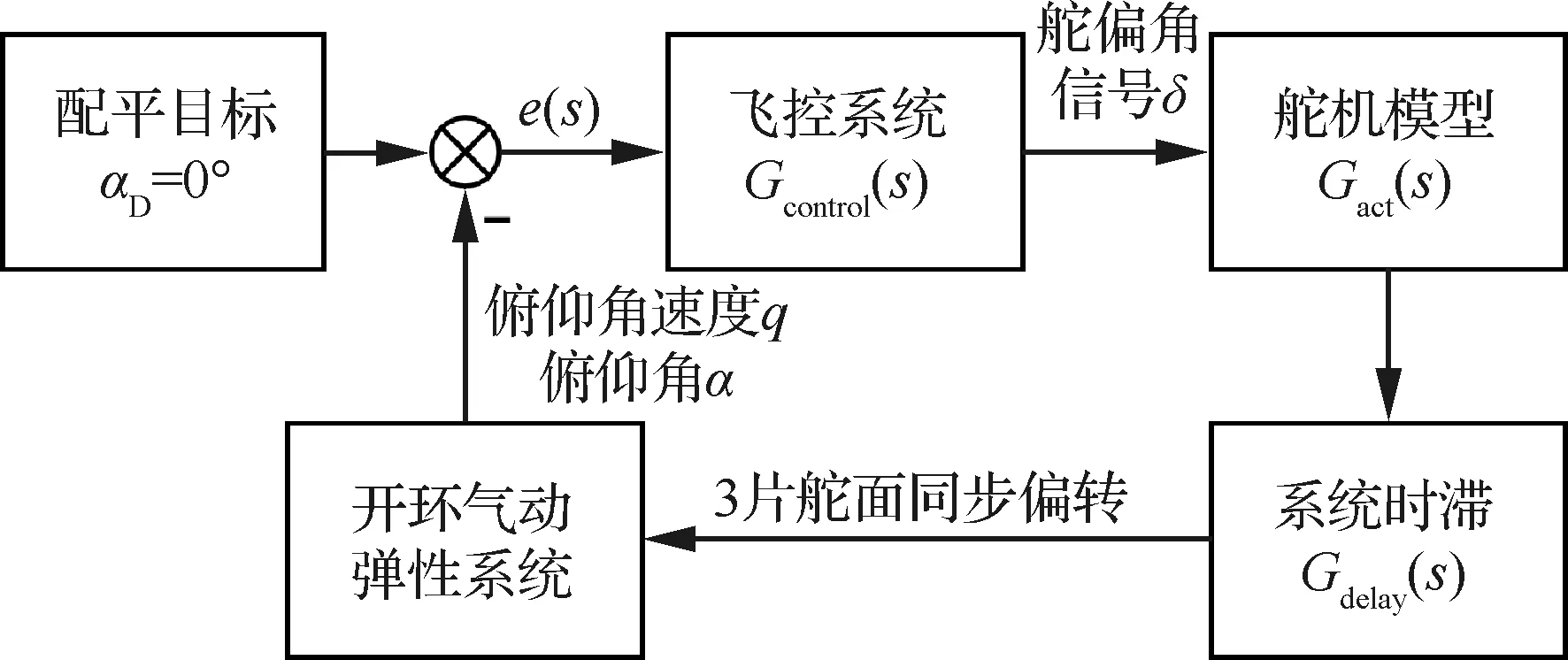
图10 气动伺服弹性模型方框图

(5)

(6)

2 结果分析

颤振试验采用风洞紊流激励，试验时风洞风速按阶梯逐渐增加，通过直吹颤振获得颤振特性参数。在此方法上，改变控制律参数，开展飞行控制律对体自由度颤振特性影响的试验研究，同时针对不同试验状态开展频域计算，进一步说明试验获得的影响规律。

试验模拟了两种刚体自由边界条件：支撑转轴位于质心位置和支撑转轴前于质心位置。其中支撑前移状态能够在一定程度上模拟俯仰和沉浮两个刚体自由度的影响，使模型的模态特性更接近刚体自由-自由对称边界情况(图11)，该状态着重于检验俯仰姿态保持控制律和计算模型的有效可靠；而质心位置支撑状态仅模拟刚体俯仰自由度，着重于开展开环及不同增益下的闭环颤振特性风洞试验研究。

图11 支撑轴前移状态

2.1 支撑轴前移状态

首先对于支撑轴前移状态可同时模拟俯仰和沉浮两个刚体自由度，使模型的模态特性更接近刚体自由-自由对称边界情况做简要说明[15]。如图12所示，当转轴不支撑在质心位置时(位于图中x′)，模型绕支撑轴的转动将包含俯仰和沉浮两个形式的运动。通过合理的选定支撑转轴前移距离l，可以实现俯仰、沉浮两个自由度的模拟。

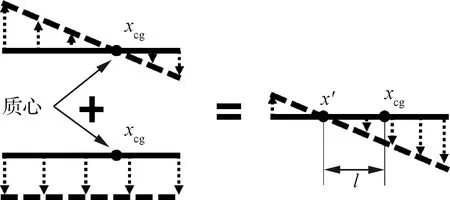
图12 刚体沉浮和俯仰运动的叠加

具体来说，仅考虑俯仰和沉浮两个刚体自由度的动力学方程：

(7)

式中：M为模型质量；R为模型俯仰惯量回转半径；Q为速压；S为参考面积；CL为升力系数；xac为质心到焦点距离；质心在前为正。

当发生颤振时，两个刚体模态做简谐振动，设解的形式分别为：Zeiωt，Θeiωt，其中Z与Θ分别表示沉浮与俯仰刚体简谐振动的幅值，ω为简谐振动频率。假设两刚体运动幅值满足Z=lΘ，代入方程可得

(8)

对比式(8)的两行，若同时成立可得

l=-R2/xac

(9)

式中：负号表示质心在后，当x′点距质心的距离l满足式(9)时，飞机在气动力作用下的沉浮俯仰运动相当于绕x′做俯仰运动。

针对本文模型，表3给出了两种边界条件下前三阶主要模态频率对比，可见模态频率非常接近。最大偏差不超过1.7%。图13给出了两种边界条件下的模态振型有限元分析结果。可见支撑前移状态的俯仰模态振型基本与自由-自由状态的俯仰加沉浮模态振型接近，同时两种支撑方式的一弯模态振型基本相同。

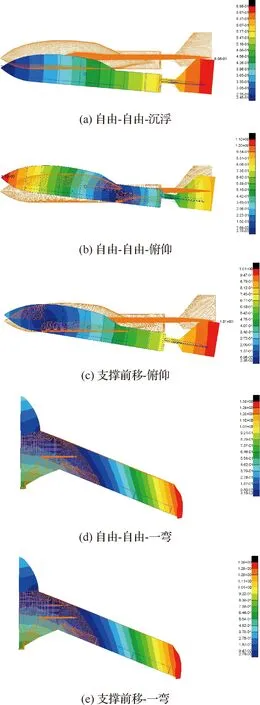
图13 支撑前移与自由-自由状态模态振型

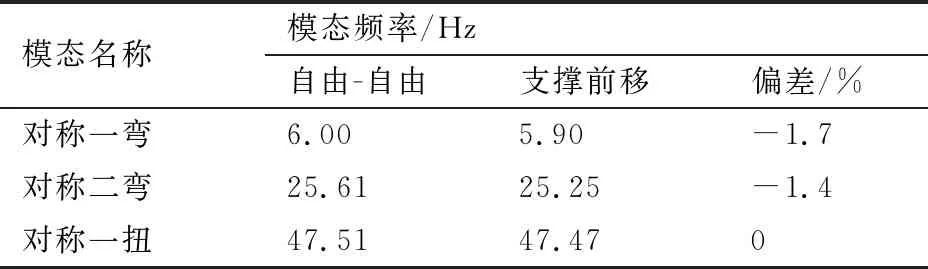
表3 支撑前移与自由-自由状态模态频率对比

基于上述分析，本文采用支撑轴前移的方式开展了俯仰沉浮自由状态的风洞试验。试验首先是验证俯仰姿态保持控制律的有效性，其次通过对比闭环试验结果与开环/闭环计算结果初步分析控制律对体自由度颤振特性的影响规律，同时检验气动伺服弹性计算模型的可靠性。

试验过程如图14所示，刚开始试验时，由于重力力矩的作用，模型位于最大限位位置，此时俯仰角约为13.4°。

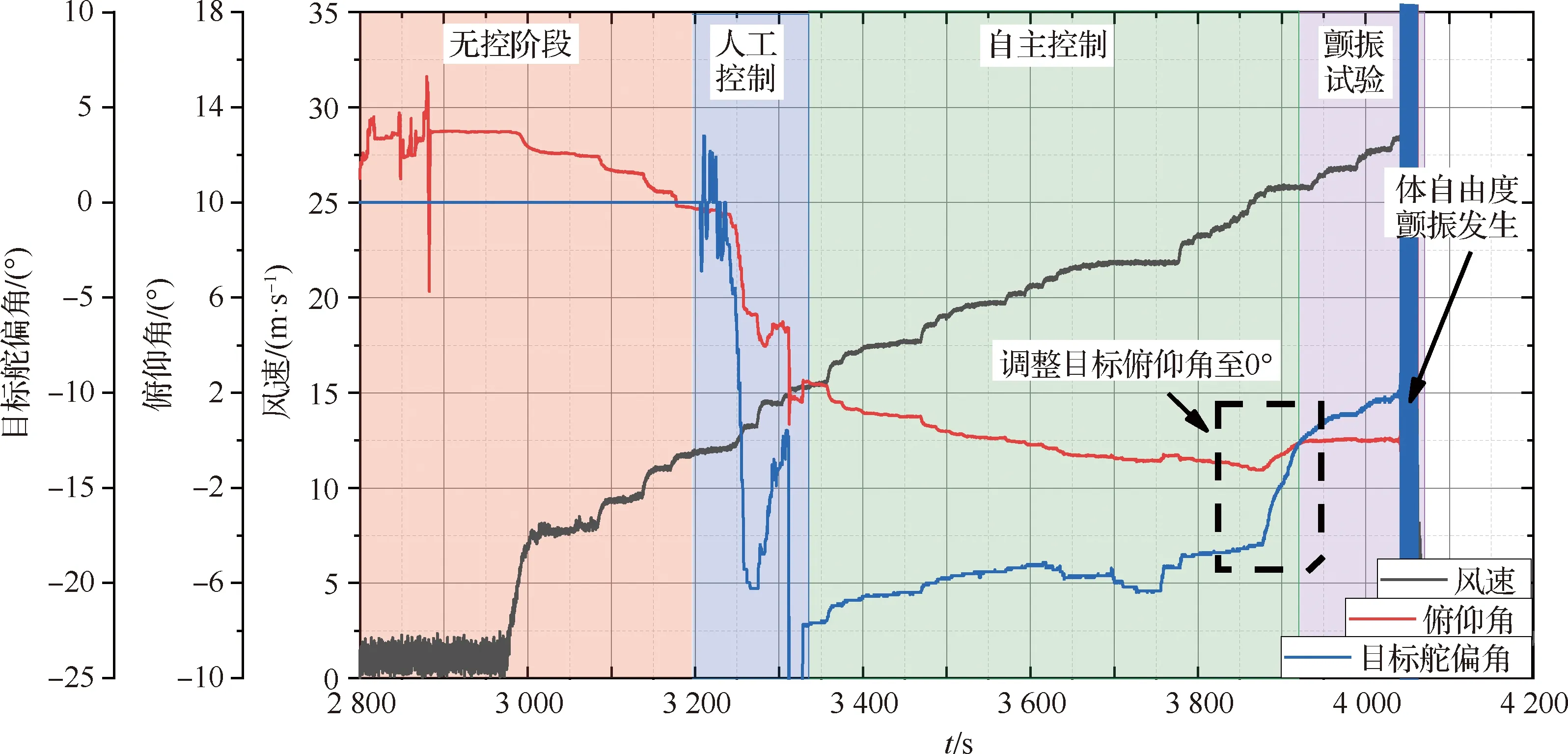
图14 支撑轴前移状态试验结果

在无控阶段，随着风速逐渐增大俯仰角降低，但由于风速仍然较低，舵效不足，打舵至最大位仍无法配平力矩，因此先保持飞控开环。

随着风速继续增大，首先通过人工控制，调整模型姿态，将模型拉起。当风速到达15 m/s后，进入自主控制阶段。可见随着风速增大，模型俯仰角由正向负降低，舵偏角相应的由负向正逐渐增加，俯仰姿态保持控制律能通过自主调节舵偏角来实现模型纵向姿态的调整与保持。

当风速到达25.7 m/s时，进入颤振试验阶段，调整目标俯仰角为0°。随着风速继续增大至28.3 m/s，体自由度颤振出现。图15给出了体自由度颤振发生时4个采集通道振动信号的频率响应结果，颤振发生时的频率约为3.7 Hz。

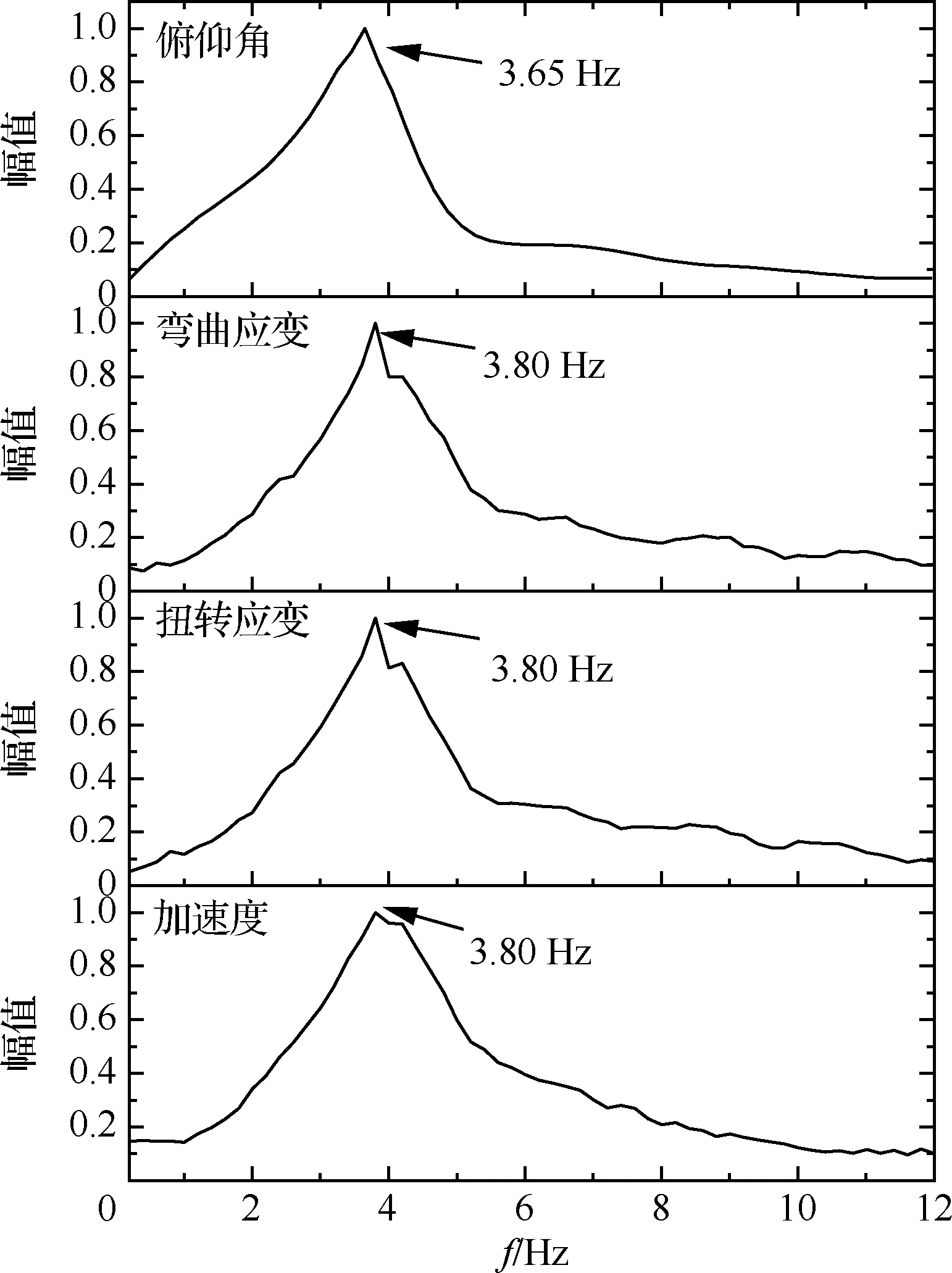
图15 频域响应试验结果

采用频域计算对控制律的影响作进一步分析，图16给出了开环与闭环模型的颤振计算结果对比，分别为阻尼比g和模态频率f随速度V的变化规律。从图16可以看出，开闭环前后的体自由度颤振发散模态均为俯仰模态，但闭环控制明显改变了模态阻尼的原有走势，闭环后的俯仰模态阻尼显著降低。计算的开环颤振速度为39.6 m/s， 颤振频率为5.04 Hz，明显高于试验获得的闭环颤振速度28.3 m/s和颤振频率3.70 Hz。计算的闭环颤振速度28.9 m/s与频率3.44 Hz，与试验吻合较好。

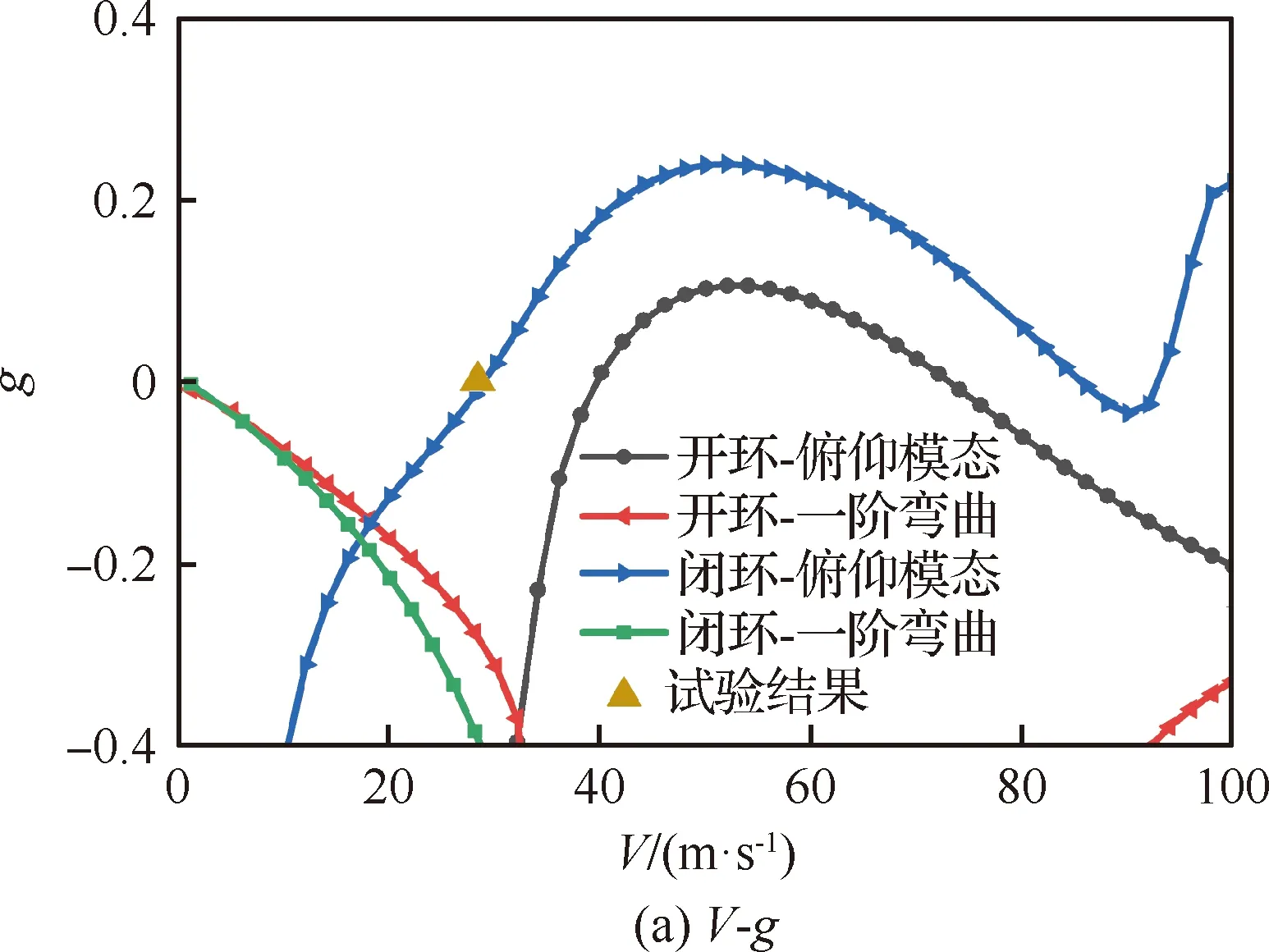
图16 开/闭环颤振V-g和V-f图

通过支撑前移状态试验一方面验证了俯仰姿态保持控制律的有效性，可实现俯仰角的自主控制，检验了所建立的气动伺服弹性计算模型的可靠。另一方面试验结果说明体自由度颤振特性受控制律影响显著，开环与闭环模型的颤振特性完全不同。

2.2 质心位置支撑状态

由于支撑前移时必须引入控制律，在不同风速下保持模型姿态，因此难以通过试验对比开环闭环前后的颤振特性变化。当支撑转轴位于质心时，模型仅存在刚体俯仰自由度。对于静稳定的模型，无需舵面参与，在开环状态仅通过模型俯仰角即可实现俯仰力矩的配平，便于开环闭环试验对比，以及控制律参数影响规律研究。因此本文在质心位置支撑状态下开展了开环及闭环不同比例回路增益KP下的风洞试验。

首先对质心位置支撑状态下的开环颤振特性进行了计算，说明该状态下同样会发生体自由度颤振。图17给出了开环状态颤振计算结果，在此状态下同样发生了由俯仰模态和一阶弯曲模态耦合造成的体自由度颤振，且发散模态分支同样为俯仰模态。此时的颤振特性与支撑前移时有所区别，颤振速度为23.7 m/s，颤振频率为1.95 Hz，较支撑前移状态偏低。由于控制律中并不包含沉浮运动相关变量，因此这并不会改变飞行控制律对体自由度颤振特性的影响机理。

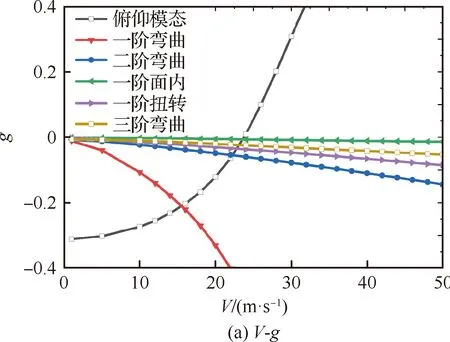
图17 沉浮运动约束时颤振计算结果

根据上述分析，开展了质心位置支撑状态的闭环颤振特性风洞试验研究。图18给出开环与不同比例环节闭环增益KP下的颤振临界风速对比，其中体自由度颤振发生时由于俯仰姿态大幅运动，空速测值瞬间降低。以此为标志从图中可见，随着KP增大，颤振速度逐渐减低。图19给出了开环以及不同KP下的频域响应试验结果，可见闭环颤振频率较开环增大，但随着KP增大基本保持不变。

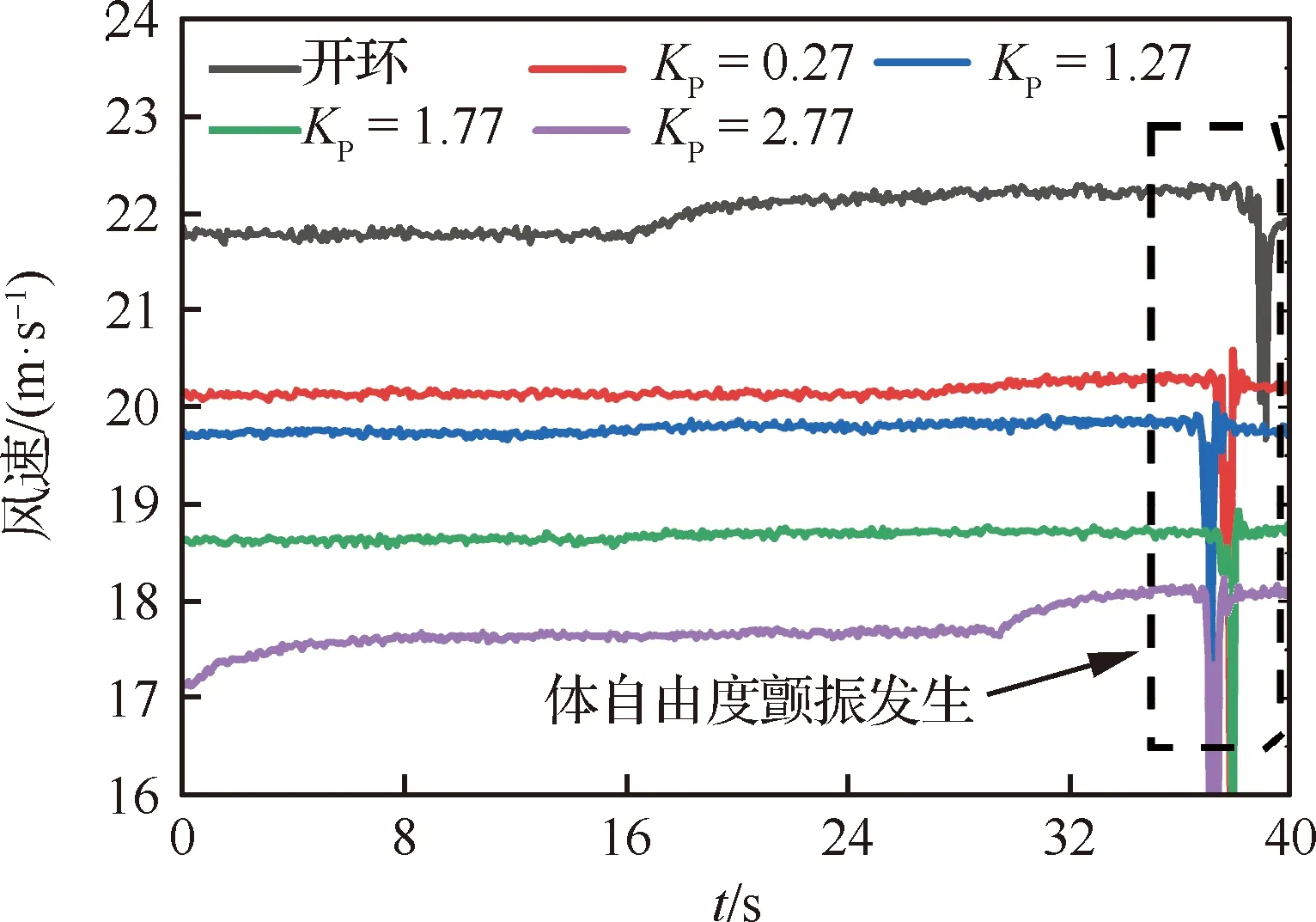
图18 不同闭环增益下的颤振临界速度

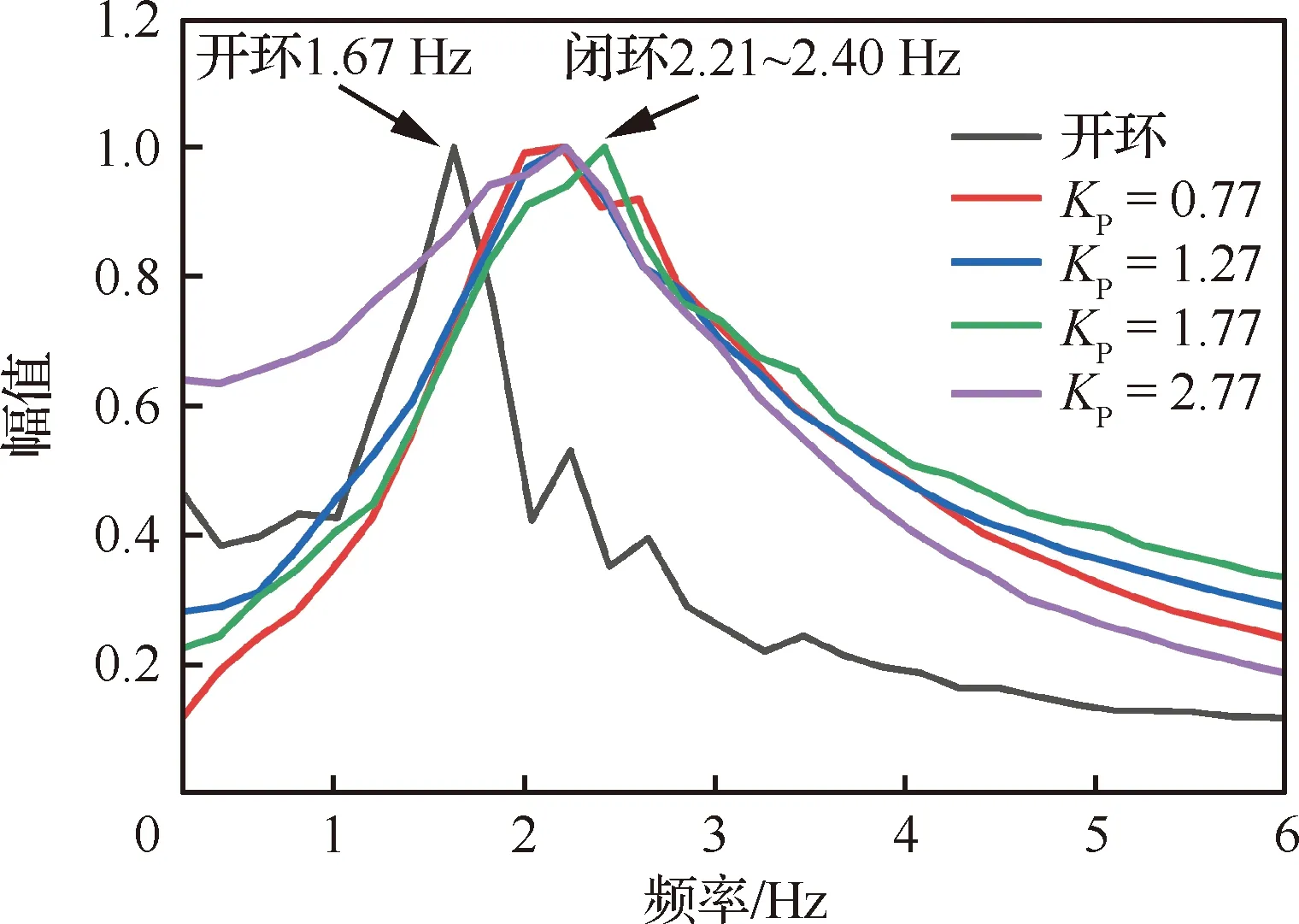
图19 不同闭环增益下的频率响应结果

采用频域计算对控制律的影响作进一步验证。图20、图21给出了不同增益下的颤振速度和频率的计算结果及其与试验结果的对比。计算结果同样获得了与试验一致的闭环控制的影响规律。在量值上计算与试验吻合较好，计算获得的颤振速度随KP增加降幅更大。

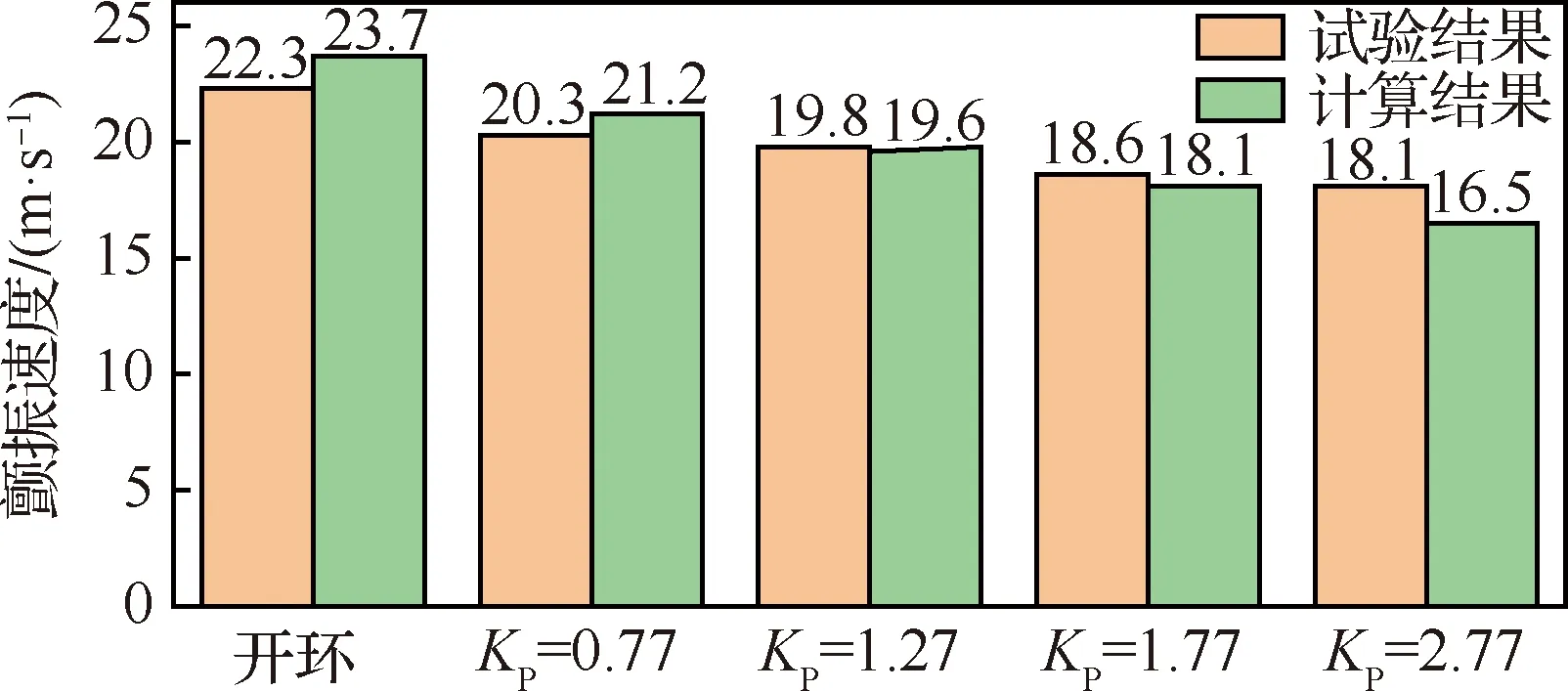
图20 不同闭环增益下的颤振速度计算结果与试验结果对比

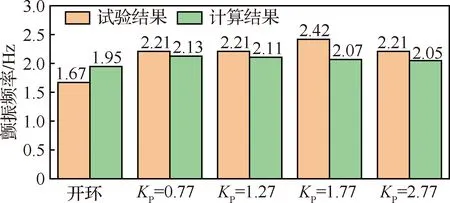
图21 不同闭环增益下的颤振频率计算结果与试验结果对比

对于俯仰姿态保持控制律影响机理的简要分析如下。

一般来说，俯仰角传动比增大会加快调节时间、减小稳态误差，但过大会使系统不稳定。俯仰角速度传动比增大，会加大俯仰阻尼、提高系统平稳性[20]。图22给出了不同闭环比例回路增益和微分回路增益下的控制律的相频特性曲线，可见随着KP增大以及KD减小，PID控制器相位超前减小，标志着俯仰角传动比增加，俯仰角速度传动比减小，因此控制响应更快，但同时系统的俯仰阻尼降低，以致体自由度颤振速度降低。从试验获得的俯仰角发散曲线中也能发现，KP越大颤振发生越突然(图23)。

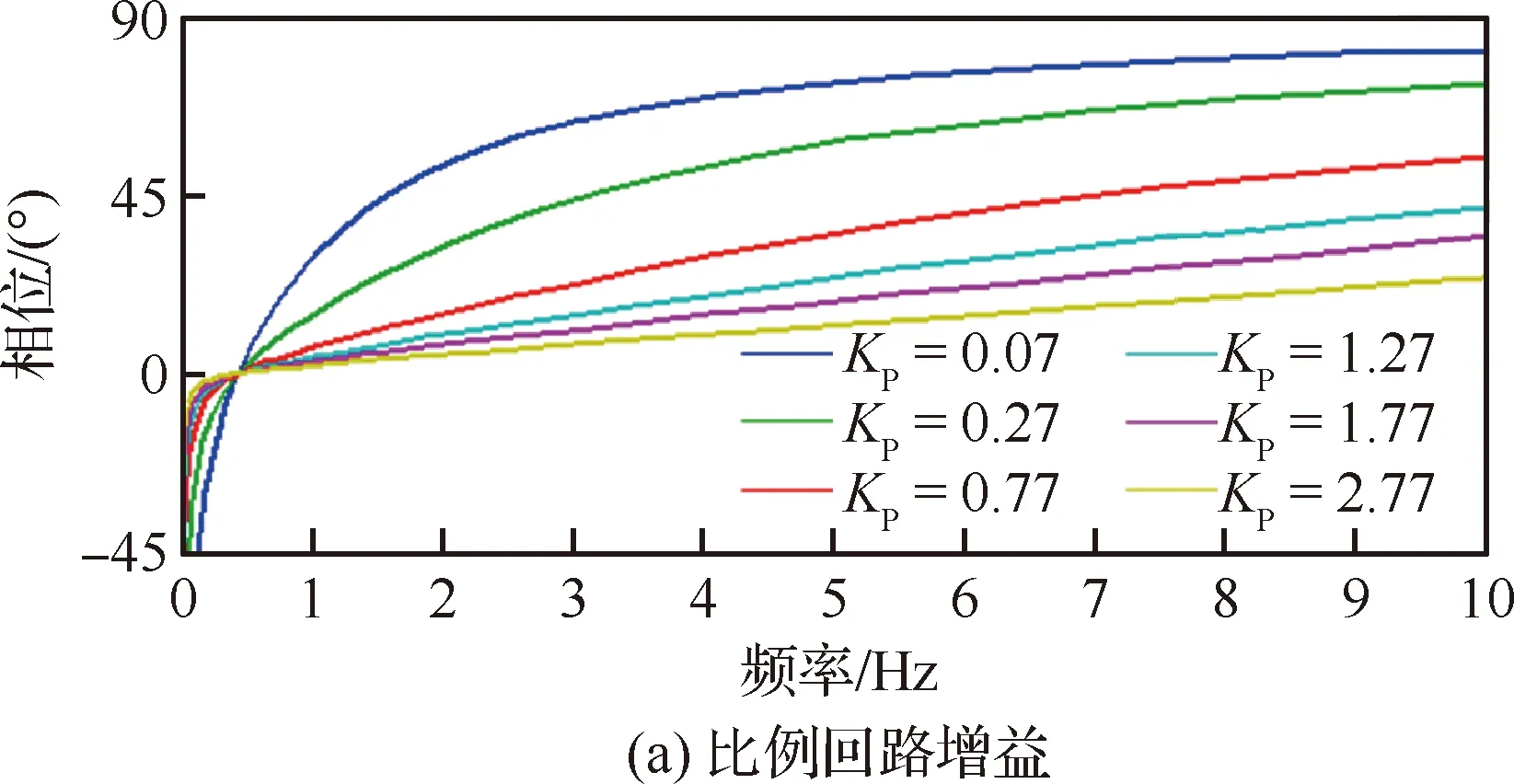
图22 不同闭环增益下的PID控制器相频特性

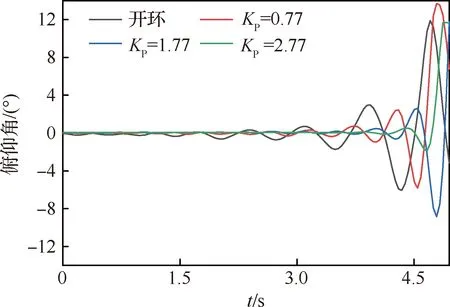
图23 不同闭环增益下的俯仰角发散曲线

根据上述针对试验结果的分析，从反方面推论可得：减小KP、增大KD将有利于颤振速度的提高。因此本文采用计算手段，分析了不同KP和KD下的颤振特性，图24给出了不同KP下的俯仰模态分支阻尼变化规律。可见模态阻尼走势的变化主要表现为平移变化，即降低KP整体增加了俯仰模态阻尼。当KP=0.07时，闭环颤振速度高于开环颤振速度，俯仰姿态保持控制律起到了颤振抑制的作用。图25给出了不同KD下俯仰模态阻尼走势的变化规律。可见随着KD增大，颤振速度也会增大，但变化量值明显小于KP的影响。从PID控制器的相频特性曲线能看出，随着KD增大，控制器相位增量越来越小，因此对颤振速度的影响也越来越小。当KD=0.20时，闭环颤振速度高于开环颤振速度，俯仰姿态保持控制律同样起到了颤振抑制的作用。综合KP和KD的变参计算分析结果表明通过设计飞机自身的飞行控制律，增大俯仰角速度传动比，增加俯仰阻尼，能实现体自由度颤振的抑制。

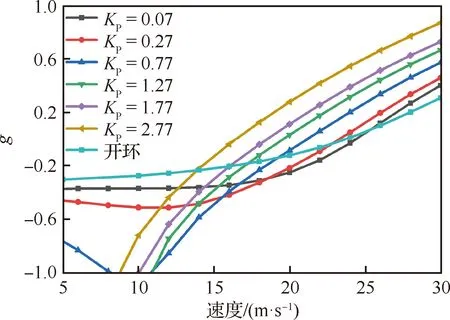
图24 不同KP下的俯仰模态阻尼变化曲线

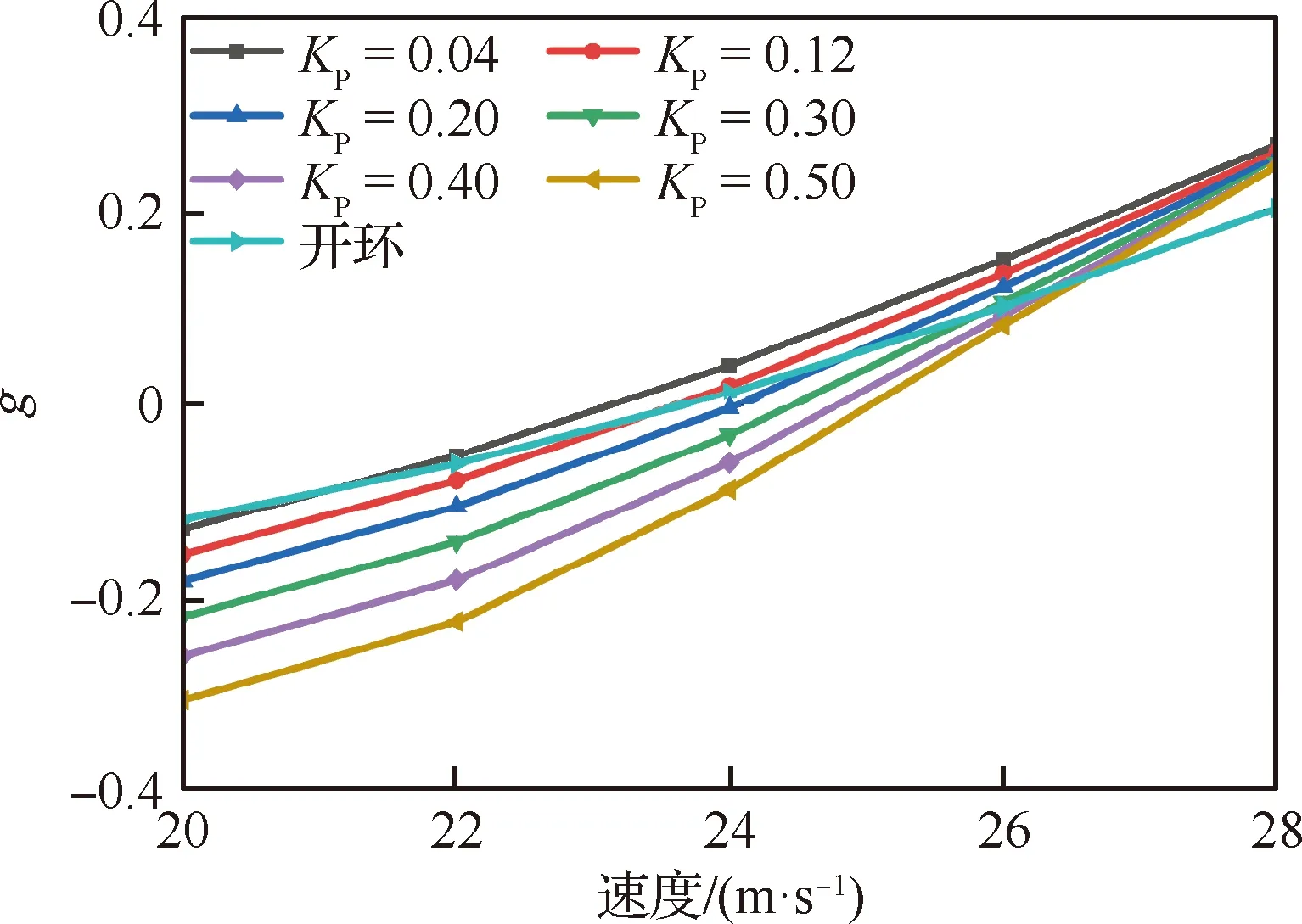
图25 不同KD下的俯仰模态阻尼变化曲线

3 结 论

1) 经风洞试验检验，本文所使用的俯仰姿态保持控制律合理有效，可实现模型俯仰姿态的自主控制。这是开展飞行控制律对体自由度颤振特性影响研究的基础。

2) 风洞试验与计算结果共同表明，体自由度颤振特性受飞行控制律影响明显，在飞行器的体自由度颤振分析中不可被忽略。就本文试验中的控制律与模型而言，闭环后颤振速度降低，颤振频率提高，且比例回路增益越大，颤振速度越低，颤振发生的越突然，但此时颤振频率基本保持不变，试验结果与计算结果在规律和量值上吻合较好。

3) 俯仰姿态保持控制律影响机理研究表明，控制律主要通过改变俯仰气动阻尼来影响体自由度颤振特性。以开环颤振速度为基准，较大的比例回路增益或较小的微分回路增益，使得俯仰角传动比大，虽然系统响应速度较快，但闭环后降低了俯仰阻尼，应用此时的飞行控制律会导致闭环颤振速度降低；而比例回路增益较小或微分回路增益较大时，俯仰角速度传动比大，飞控闭环后能起到增加俯仰阻尼、抑制体自由度颤振的作用。