曲线波纹钢腹板组合箱梁剪力滞翘曲位移函数研究

王连广，佟永晨，陈力栋

(东北大学资源与土木工程学院，辽宁 沈阳 110819)

波纹钢腹板组合箱梁具有较好的抗整体和局部剪切屈曲的能力，抗剪性能良好，且波纹钢腹板重量轻，避免了混凝土腹板质量过大的缺点，较大程度减小了传递到下部结构的荷载，降低工程成本[1-3]。纵向刚度较小的波纹钢腹板能有效地提高体内以及体外的预应力利用效率[4]。在外部荷载作用下，由于波纹钢腹板有较小的厚度，产生的剪切变形更明显[5]。由于结构变形沿其横向宽度方向的不均匀分布，在组合箱梁结构中广泛存在剪力滞后行为，并导致结构不稳定和破坏[6]。目前，研究学者选择众多类型函数作为研究剪力滞的翘曲位移函数，文献[7-10]分别采用n次抛物线型、余弦函数型和经验公式作为研究剪力滞效应的翘曲位移函数，并针对不同函数类型提出不同求解建议。不同剪力滞翘曲位移函数只是针对直线箱梁，而非曲线箱梁。附加外荷载的情况下，由于曲线梁曲率的存在，会产生扭转变形，导致横截面产生不对称的正应力。因此对于曲线组合箱梁而言，研究剪力滞效应时选择的翘曲位移函数同直线箱梁存在差异。曲线箱梁会产生强烈的弯扭耦合变形，分析剪力滞效应时需要考虑滑移效应和弯扭耦合[11]效应所带来的影响。笔者以曲线波纹钢腹板组合箱梁作为研究分析对象，对其剪力滞效应翘曲位移函数的选择基于能量原理[12-14]，建立曲线波纹钢腹板组合箱梁的剪力滞效应抛物线型及余弦型翘曲位移函数计算公式[15-16]。并采用加权余量法，对曲线波纹钢腹板组合箱梁实取截面进行计算分析。

1 抛物线型及余弦型翘曲位移函数

波纹钢腹板组合箱梁构造如图1所示。

图1 波纹钢腹板组合箱梁构造图Fig.1 Structural drawing of corrugated steel web composite box girder

根据波纹钢腹板组合箱梁的特点，基于能量原理研究剪力滞效应时假定：①混凝土顶板底板与波纹钢腹板竖向完全贴合；②剪力滞效应只在竖向弯曲中考虑；③忽略混凝土顶底板的竖向挤压应变和横向应变[17]；④波纹钢腹板组合箱梁各部分均为线弹性材料，并保持弹性工作状态。组合箱梁截面示意图如图2所示。

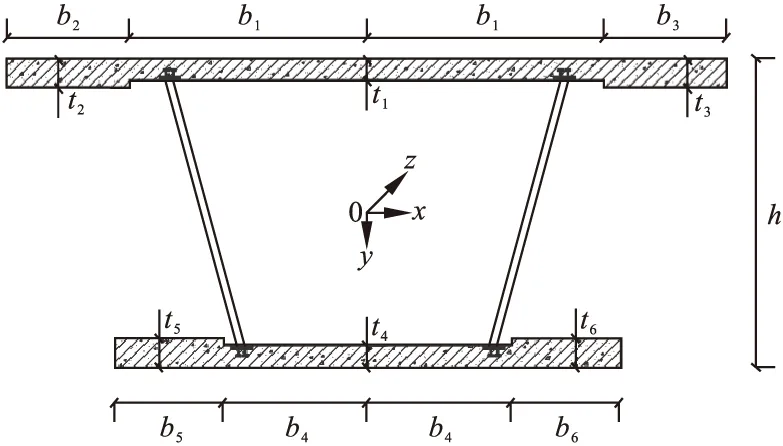
图2 截面尺寸及坐标示意图Fig.2 Section size and coordinates

1.1 抛物线型翘曲位移函数

组合箱梁顶板底板假设6个不同剪力滞翘曲位移函数wi(x,y,z)(i=1,2,3,4,5,6)用来描述顶底板的纵向位移沿板宽方向的变化情况，并考虑竖向挠度位移和扭转位移的影响。

剪力滞翘曲位移函数设置：

(1)

式中：bi(i=1,4)为混凝土板宽度的一半；bi(i=2,3,5,6)为混凝土悬臂板宽度；Wi(z)(i=1,2,3,4,5,6)为翼缘板纵向转角差函数；hi(i=1,2,3,4,5,6)为区域形心至截面形心的距离；ζi为边界条件与翼缘板宽度不同情形下的修正系数[18]。

由于受曲率的影响，曲线组合箱梁的几何方程由Timoshenko给出[19]：

轴向应变为

(2)

水平曲率为

(3)

竖向曲率为

(4)

扭率为

(5)

式中：u为x方向位移；v为y方向位移；w为z方向位移，φ为扭转角。

根据假定，混凝土顶底板产生的整正应变εz是满足平截面假定的刚性平面产生的正应变εz1与剪力滞翘曲位移产生的正应变εz2的和。正应变差值越大，剪力滞翘曲位移产生的正应变差值越大，剪力滞效应越明显。

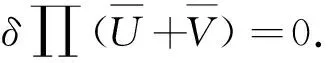
(6)

根据最小势能原理，体系总势能表达式为

(7)

当δπ=0时，在外部荷载作用下，结构保持平衡状态，采用分部积分法并考虑弯扭、剪力滞后以及界面滑移耦合得到控制微分方程：

(8)

(9)

(10)

(11)

(12)

(13)

多个位移函数耦合的高阶常系数微分方程联立很难求得闭合解，因此考虑数值解代替。笔者采用加权余量法进行求解。

根据边界条件假设试函数和权函数均为

v=vnsin(πz/l)；φ=φnsin(πz/l)；

Wi=Wincos(πz/l),(i=1,2,3,4,5,6)；

ηi=ηincos(πz/l),(i=1,2).

代入(8)～(13)中得：

(14)

采用加权余量法求得混凝土顶底板不同宽度处的正应力值：

顶板应力为

(15)

底板应力为

(i=4,5,6).

(16)

1.2 余弦型翘曲位移函数

基于抛物线型剪力滞翘曲位移的公式推导的基础上，推导出曲线波纹钢腹板组合箱梁余弦型剪力滞翘曲位移函数[20-21]。

剪力滞翘曲位移函数设置：

(17)

式中：α1=α4=1;αi=(bi/b1)2(i=2,3)；αi=(bi/b4)2(i=5,6)；ui(z)为翼缘板纵向最大位移差函数。

基于能量法推导出控制微分方程和边界条件，采用加权余量法得出混凝土顶底板不同宽度处表达式：

顶板应力为

(18)

底板应力为

(19)

2 算例分析

笔者采用推导的控制微分方程式(8)～(13)和化简的代数方程式(15)、(16)、(18)、(19)计算，简化起见，令b5=b6=0，t5=t6=0，wi=w(z)(i=1,2,3,4,5,6)，b1=b4=1 000 mm，b2=b3=400 mm，ti=50 mm(i=1,2,3,4)。

曲线波纹钢腹板组合箱梁截面尺寸与腹板波纹形状如图3所示。

图3 波纹钢腹板组合箱梁截面尺寸与形状示意图Fig.3 Schematic diagram of section size and shape of corrugated steel web composite box girder

计算得：Kd=1 345 N/mm，中和轴位置：hi=183 mm(i=1,2,3)，h4=217 mm，h5=h6=0，Gc=1.44×104MPa，Gs=7.69×104MPa，Geff=7.0×104MPa，Eeff=186.6 MPa，Ieff=14 696 267 mm4，fc1=-1.08×10-4，fc2=-1.51×10-4，扇形惯性矩：EIw=3.28×1019mm6，组合梁抗扭惯性矩：GckTc+GskTs=3.3×1014MPa，曲线梁曲率半径：R=5×104mm，l=5 000 mm，均布荷载：160 N/mm，qn=203.7 N/mm，ζ1=ζ4=1，ζ2=ζ3=0.16。

式(10)可简化为：

(20)

n取2～7，设剪力滞翘曲位移函数按余弦变化，解方程得出计算结果如表1所示。

表1 曲线波纹钢腹板箱梁计算结果Table 1 Calculate results of curved corrugated steel web box girder

其中沿着x轴正方向滑移得到数值为正的滑移量η1n，沿着x轴负方向滑移得到数值为负的滑移量η2n。

跨中截面不同宽度处顶底板抛物线型和余弦型函数正应变对比分析如图4所示。

图4 顶板底板位移函数对比分析Fig.4 Comparative analysis of displacement functions of roof plate and bottom plate

由图4(a)可知，在n取值从2到7的过程中，顶板应变曲线呈逐渐逼近的规律而非远离，说明顶板剪力滞翘曲函数按n次抛物线设定是收敛的。在顶板中点位置、翼缘板腹板交点位置和悬臂板边缘，按n次抛物线规律变化的考虑剪力滞效应的应变差别不大，即n的取值对应变的影响大小有限。在上翼缘板中，当剪力滞翘曲函数的变化规律为余弦函数时，顶板中点与翼缘板腹板交点、翼缘板腹板交点和悬臂板边缘的应变差值较n次抛物线函数变化形式更大，说明按照余弦函数变化的剪力滞翘曲函数在整块顶板会得出更明显的考虑剪力滞的应变变化曲线。所有曲线中同一位置最大和最小应变差值为4.4×10-5，顶板沿板宽的实际应变规律更符合哪条应变曲线需由试验或精细化模型模拟得出。由图4(b)可知，在n取值从2到7的过程中，底板应变曲线呈逐渐逼近的规律而非远离，说明剪力滞翘曲函数按n次抛物线设定是收敛的。 在底板中点位置，按n次抛物线规律变化的考虑剪力滞效应的应变差别略大，达到3.4×10-5，但在底板腹板交点位置处变化不大。当剪力滞翘曲函数的变化规律为余弦函数时，在悬臂板边缘较n次抛物线函数变化形式更大，说明按照余弦函数变化的剪力滞翘曲函数在整块顶板会得出更明显的考虑剪力滞的应变变化曲线。所有曲线中最大和最小应变差值为5.4×10-5，底板沿板宽的实际应变规律更符合哪条应变曲线需由试验或精细化模型模拟得出。

3 结 论

(1)曲线波纹钢腹板剪力滞翘曲函数按n次抛物线设定是收敛的。

(2)剪滞翘曲函数按照n次抛物线变化考虑剪力滞时，顶板不同位置应变差值差异不大，小于2.0×10-5；底板中点位置应变差值差异较大，达到3.4×10-5，其他位置变化不大，故对底板n的考虑需区分应变考察的位置。

(3)曲线波纹钢腹板组合箱梁应变曲线中最大与最小应变差值为4.4×10-5，底板差值为5.4×10-5，应变随剪力滞翘曲位移函数的不同选择呈现出较大的差别，顶板底板沿板宽的实际应变规律更符合哪条应变曲线需由试验或精细化模型模拟得出。